2.2整式的加减(共4课时)
文档属性
| 名称 | 2.2整式的加减(共4课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-14 00:00:00 | ||
图片预览




文档简介
课题:整式的加减(1)—同类项、合并同类项 课型:新课 课时:1课时
【教学目标】
1.理解同类项的概念,在具体情景中,认识同类项。
2. 理解合并同类项的概念,领会合并同类项法则。
【重点难点】
重点:理解同类项的概念;领会合并同类项法则。
难点:根据同类项的概念在多项式中找同类项。
【导引自学】
1、⑴、5个人+8个人=
⑵、5只羊+8只羊=
⑶、5个人+8只羊=
2、观察下列各单项式,把你认为相同类型的式子归为一类。
8x2y, -mn2, 5a, -x2y, 7mn2, , 9a, -, 0, 0.4mn2, ,2xy2.
观察归为一类的式子,思考它们有什么共同的特征?说出各自的分类标准。
3、运用有理数的运算律计算:⑴100×2+252×2= 100×(-2)+252×(-2)=
100t+252t=
⑵填空 : ①100t-252t=( )t ②3x+2 x=( ) x
③3ab2-4a b=( )a b
思考:如何化简式子:4x2+2x+7+3x-8x2-2
4、什么叫做同类项?什么叫做合并同类项?合并同类项法则是什么?
【双基自测】
1:判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。 ( ) (2)2ab与-5ab是同类项。 ( )
(3)3x2y与-yx2是同类项。 ( ) (4)5ab2与-2ab2c是同类项。 ( )
(5)23与32是同类项。 ( )
2. 若2amb2m+3n与ab8可以合并成一项,则m与 n的值分别是______
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
同类项:
合并同类项:
如何合并同类项:
三、范例剖析,合作探究。
例1:合并下列多项式中的同类项:
解:
例2:(1)求多项式2x2-5x+ x +4x-3 x-2的值,其中x=
⑵求多项式3a+abc-c-3a+c的值,其中a= , b=2, c=-3
例3.(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解
四、课堂反馈,达标测评。
1.如果是同类项,那么 . .
2.已知-7xmy与0.5xyn+1和是一个单项式,则m= ,n= ,这个和为 。
3.若单项式-2xmyn与ax3y2的和为0,则m= ,n= ,a= .
4.下列各对不是同类项的是( )
A -3 xy与2 xy B -2x y与 3 x y C -5 xy与3y x D 3m n与2m n
5.合并同类项正确的是( )
A 4a+b=5ab B 6x y-6 yx=0 C 6 x-4 x=2 D 3 x+2 x=5 x
6.已知-2ambc2与4a3bnc2是同类项,求多项式3m2n-2mn2-m2n+mn2的值
7.若把(s+t)、(s-t)分别看作一个整体,指出下面式子中的同类项。
(1)(s+t)-(s-t)-(s+t)+(s-t);
(2)2(s-t)+3(s-t)2-5(s-t)-8(s-t)2+s-t。
解
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
(一) 必做题
1、若是同类项,则m=____,n=____。
2、在中,与__同类项,与__是同类项,-2与__是同类项。
3、可以合并成一项,那么m+n= .
4、化简(n是正整数)后的结果为 .
5、在排成每行七天的日历表中取下一个3×3方块.若所有日期数之和为189,则n的值为( )
A.21 B.11 C.15 D.9
6、下列各组中,不是同类项的是( )
A、 B、 C、 D、
7、若-x2yn与3yx2是同类项,则n的值为( )A、-1;B、3;C、1;D、2.
8、下列等式正确的是( )
A、a5+a5=2a10; B、a5+a5=a10 ; C、a5+a5=2a5; D、x2y+xy2=2x3y3
9、合并的结果为( )
A、;B、;C、;D、.
10、合并同类项:
(1)
(2)(a-b)2+3(a-b)-(a-b)-7(a-b)2
(二)选作题
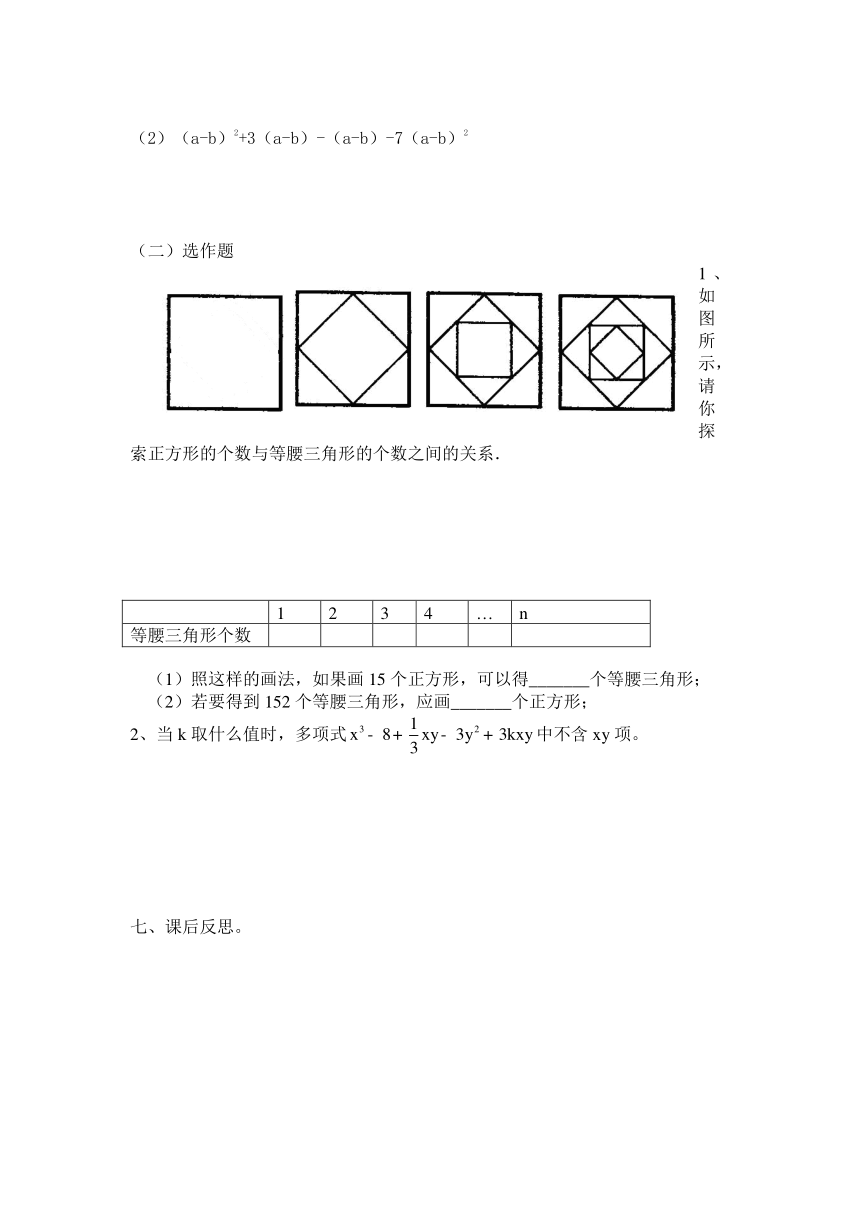
1、如图所示,请你探索正方形的个数与等腰三角形的个数之间的关系.
正方形个数
1
2
3
4
…
n
等腰三角形个数
(1)照这样的画法,如果画15个正方形,可以得_______个等腰三角形;
(2)若要得到152个等腰三角形,应画_______个正方形;
2、当k取什么值时,多项式中不含xy项。
七、课后反思。
课题:整式的加减(2)--- 去括号 课型:新课 课时:1课时
【教学目标】
1.理解去括号时符号变化的规律,会用去括号法则进行计算.
2.通过类比,让我们经历去括号法则的探索过程,掌握去括号的方法.
3.通过观察、猜想、整理,培养我们的归纳能力;通过合作学习、讨论,培养我们学会与他人交流的意识和能力.
【重点难点】
重点:
难点:
【导引自学】
1. 在格尔木到拉萨路段,如果列车通过冻土地段要t小时,那么它通过非冻土地段的时间为(t-0.5)小时,于是,冻土地段的路程为100t千米,非冻土地段的路程为120(t-0.5)千米,因此,这段铁路全长为(单位:㎞):
冻土地段与非冻土地段相差(单位:㎞):
2.乘法分配律如何用字母表示?
3.利用乘法分配律计算:
12×(+)= —12×(-)=
2×(x+8)= -3(3x+4)= -7(7y-5)=
4.通过刚才的计算,你能够发现去括号时符号的变化规律吗?项数呢?你明白它们变化的依据吗?
【双基自测】
计算:
⑴ 2(4x-0.5) ⑵-3(1-x) ⑶-x+(2x-2)-(3x+5)
⑷3a +a-(2 a -2a) +(3a-a) ⑸ (5a+4b+7c)-(5c-3b-6a)
⑹ (8xy-x+y)-(x-y+8xy) ⑺(2 x-+3x) -4(x-x+)
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
去括号法则:
(1)、如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(2)、如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
特别地,+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3).
+(x-3)=x-3 (括号没了,括号内的每一项都没有变号)
-(x-3)=-x+3 (括号没了,括号内的每一项都改变了符号)
注意事项
(1)去括号规律要准确理解,去括号应对括号的每一项的符号都予考虑,做到要变都变;要不变,则谁也不变;
(2)括号内原有几项去掉括号后仍有几项.
三、范例剖析,合作探究。
例1.化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b).
例2:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50㎞/h,水流速度是a㎞/h。
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
四、课堂反馈,达标测评。
1、判断:下列去括号有没有错误?若有错,请改正:
(1) a2-(2a-b+c)=a2-2a-b+c; (2) -(x-y)+(xy-1)=-x-y+xy-1.
2、去括号-[a-(b-c)].
3、先去括号,再合并同类项:
(1)(2x-3y)+(5x+4y); (2) (8a-7b)-(4a-5b);
(3)a-(2a+b) -2(a-2b); (4)3(5x+4)-(3x-5);
(5)(8x-3y)-(4x+3y-z)+2z; (6)2-(1+x)+(1+x+x2-x2);
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、根据去括号法则,在横线上填上“+”或“-”
(1)
(2)
(3)
(4)
2、化简:
3、数在数轴上的位置如图所示,化简:
4、化简的最后结果是( )
A. B. C. D.
5、下列去括号中正确的是( )
A. B.
C. D.
6、已知,那么的值为( )
A.80 B.10 C.210 D.40
7、减去等于的代数式是( )
A. B. C. D.
8、化简:
(1) (2)
七、课后反思。
课题:整式加减(3 )——化简求值 课型:新课 课时:1课时
【教学目标】
1.让学生从实际背景中去体会进行整式的加减的必要性,并能灵活运用整式的加减的步骤进行运算。
2.掌握整式的化简求值题解题步骤与方法
3.培养学生审题、分析、归纳、总结以及概括能力。养成仔细、严谨数学解题习惯。
【重点难点】
重点:准确进行整式加减运算
难点:准确进行整式加减运算
【导引自学】
去括号法则是什么?试举两例加以说明。
式子-7.5+3.16+-15两种读法是什么?
3.下列式子可以看着哪两个整式的和(或差)?如何化简?
(1)(x+y)—(2x-3y) (2)2
整式加减的一般步骤是什么?
【双基自测】
计算:
(1)3xy—4xy—(—2xy); (2)—ab—a+ a—(—ab)
(3)(-x+2x+5)+(4x-3-6x) (4)(3a-ab+7)-(-4a+2ab+7)
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
整式加减的一般步骤可以总结为:
(1)如果有括号,那么先去括号。(去括号时要认真检查符号和项数)
(2)如果有同类项,再合并同类项。
三、范例剖析,合作探究。
例1: 求 x-2(x-y2)+(-x+y2)的值,其中x=-2,y=
例2:已知多项式A=4a2+5b,B=-3a2-2b,计算2A-B的结果
四、课堂反馈,达标测评。
1.先化简,再求值
2.
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、化简:(1)(x+y)—(2x-3y) (2)2
(3)―2y3+(3xy2―x2y)―2(xy2―y3) (5)
(6)
2、求整式x2―7x―2与―2x2+4x―1的差。
3、化简求值:(2x3―xyz)―2(x3―y3+xyz)+(xyz―2y3),其中x=1,y=2,z=―3。
4、一个多项式加上2x2-x3-5-3x4得3x4-5x3-3,求这个多项式。
5、已知A+B=3x2-5x+1,A-C=-2x+3x2-5,当x=2时,求B+C的值。
6、如果多项式8x2-3x+5与多项式3x2+4mx2-5x+3相加后不含x2项,求m的值。
7、小文在计算某多项式减去的差时,误认为是加上,求得答案是。
(1)求这个多项式。(2)正确答案是多少?
10.若多项式
的值与无关,求的值。
6、各位数字是a,十位数字是b,百位数字是c的三位数与把该三位数的个位数字与百位数字对调位置后所得的三位数的差为 。
七、课后反思。
课题:整式的加减(4)——实际问题 课型:新课 课时:1课时
【教学目标】
1、通过实际问题列代数式并运用整式加减法则进行运算。
2、通过小组合作,准确理解题意,正确列出式子和计算出结果。
3、培养细心、耐心的数学素养,加强学生计算能力,进而提高学生学数学的兴趣。
【重点难点】
重点:通过实际问题正确列出式子和计算出结果。
难点:通过实际问题正确列出式子和计算出结果。
【导引自学】
什么是同类项?合并同类项的法则是什么?
怎样去括号?去括号法则是什么?
整式加减的一般步骤是什么?
4. 某学生合唱团出场时第一排站了n名,从第二排起每一排都比前一排多一人。
(1) 一共站了四排,则该合唱团一共有多少名学生参加?
(2) 一共站了m排,则该合唱团一共有多少名学生参加?
通过此例,在解决实际问题时我们如何正确得出结果?
【双基自测】
1. 一种笔记本的单价是x元,圆珠笔的单价是y元,小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支。买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
2. 做大小两个长方形纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
引导学生,在解决实际问题时,要明确:
(1)认真审题,题目告诉了什么。要解决问题必须知道什么。
(2)学会分步骤解题,每一步必须弄得清清楚楚,不要一步写出综合算式
切忌题目没有读懂,盲目写过程,写了改,改了写。心情急躁、没有耐心、不细心的人学不好数学
三、范例剖析,合作探究。
例1:某地电话拨号上网有了两种收费方式,用户可以任取其一:
(A)计时制:0.05元/分;
(B)包月制:50元/月(只限一部宅电上网),此外,每种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网时间为x小时,请你写出每种收费方式下该用户应该支付的费用。
(2)若某用户估计一个月内上网时间为20h,你认为采用哪种方式合算。
例2:(1)任意写两位数; (2)交换这个两位数的十位数字和个位数字,又得到一个两位数;
(3)求这两个数的和。
再写几个两位数按上面的过程试一试,这些和有什么规律?
你能证明你的猜想吗?
四、课堂反馈,达标测评。
1、A和B两家公司都准备向社会招聘人才,两家公司招聘条件基本相同,只有工资待遇有如下差异:A公司年薪10000元,每年加工龄工资50元,B公司半年年薪5000元,每半年家工龄工资50元,从经济收入的角度考虑,选择哪家公司有利?
2、(1)任意写一个三位数;(2)交换它的百位数字与个位数字,又得到一个数两个数相减;
(3)两个数相减后的结果有什么规律,这个规律对任意一个三位数都成立吗?
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、学校计划修建一个如图1所示的喷水池,但由于占地太多,需改建如图2的形状,且外圆直径不变,只是担心原来备好的材料不够。
(1)请你比较两种方案,哪一种需用的材料多(即比较哪个周长更长)?
(2)由以上结论,请推测:若题目中的三个小圆改为n个小圆,结论是否不变?那么现在要在外圆内修四个小圆,结果怎样?
七、课后反思。
【教学目标】
1.理解同类项的概念,在具体情景中,认识同类项。
2. 理解合并同类项的概念,领会合并同类项法则。
【重点难点】
重点:理解同类项的概念;领会合并同类项法则。
难点:根据同类项的概念在多项式中找同类项。
【导引自学】
1、⑴、5个人+8个人=
⑵、5只羊+8只羊=
⑶、5个人+8只羊=
2、观察下列各单项式,把你认为相同类型的式子归为一类。
8x2y, -mn2, 5a, -x2y, 7mn2, , 9a, -, 0, 0.4mn2, ,2xy2.
观察归为一类的式子,思考它们有什么共同的特征?说出各自的分类标准。
3、运用有理数的运算律计算:⑴100×2+252×2= 100×(-2)+252×(-2)=
100t+252t=
⑵填空 : ①100t-252t=( )t ②3x+2 x=( ) x
③3ab2-4a b=( )a b
思考:如何化简式子:4x2+2x+7+3x-8x2-2
4、什么叫做同类项?什么叫做合并同类项?合并同类项法则是什么?
【双基自测】
1:判断下列说法是否正确,正确地在括号内打“√”,错误的打“×”。
(1)3x与3mx是同类项。 ( ) (2)2ab与-5ab是同类项。 ( )
(3)3x2y与-yx2是同类项。 ( ) (4)5ab2与-2ab2c是同类项。 ( )
(5)23与32是同类项。 ( )
2. 若2amb2m+3n与ab8可以合并成一项,则m与 n的值分别是______
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
同类项:
合并同类项:
如何合并同类项:
三、范例剖析,合作探究。
例1:合并下列多项式中的同类项:
解:
例2:(1)求多项式2x2-5x+ x +4x-3 x-2的值,其中x=
⑵求多项式3a+abc-c-3a+c的值,其中a= , b=2, c=-3
例3.(1)水库中水位第一天连续下降了a小时,每小时平均下降2cm;第二天连续上升了a小时,每小时平均上升0.5cm,这两天水位总的变化情况如何?
(2)某商店原有5袋大米,每袋大米为x千克,上午卖出3袋,下午又购进同样包装的大米4袋,进货后这个商店有大米多少千克?
解
四、课堂反馈,达标测评。
1.如果是同类项,那么 . .
2.已知-7xmy与0.5xyn+1和是一个单项式,则m= ,n= ,这个和为 。
3.若单项式-2xmyn与ax3y2的和为0,则m= ,n= ,a= .
4.下列各对不是同类项的是( )
A -3 xy与2 xy B -2x y与 3 x y C -5 xy与3y x D 3m n与2m n
5.合并同类项正确的是( )
A 4a+b=5ab B 6x y-6 yx=0 C 6 x-4 x=2 D 3 x+2 x=5 x
6.已知-2ambc2与4a3bnc2是同类项,求多项式3m2n-2mn2-m2n+mn2的值
7.若把(s+t)、(s-t)分别看作一个整体,指出下面式子中的同类项。
(1)(s+t)-(s-t)-(s+t)+(s-t);
(2)2(s-t)+3(s-t)2-5(s-t)-8(s-t)2+s-t。
解
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
(一) 必做题
1、若是同类项,则m=____,n=____。
2、在中,与__同类项,与__是同类项,-2与__是同类项。
3、可以合并成一项,那么m+n= .
4、化简(n是正整数)后的结果为 .
5、在排成每行七天的日历表中取下一个3×3方块.若所有日期数之和为189,则n的值为( )
A.21 B.11 C.15 D.9
6、下列各组中,不是同类项的是( )
A、 B、 C、 D、
7、若-x2yn与3yx2是同类项,则n的值为( )A、-1;B、3;C、1;D、2.
8、下列等式正确的是( )
A、a5+a5=2a10; B、a5+a5=a10 ; C、a5+a5=2a5; D、x2y+xy2=2x3y3
9、合并的结果为( )
A、;B、;C、;D、.
10、合并同类项:
(1)
(2)(a-b)2+3(a-b)-(a-b)-7(a-b)2
(二)选作题
1、如图所示,请你探索正方形的个数与等腰三角形的个数之间的关系.
正方形个数
1
2
3
4
…
n
等腰三角形个数
(1)照这样的画法,如果画15个正方形,可以得_______个等腰三角形;
(2)若要得到152个等腰三角形,应画_______个正方形;
2、当k取什么值时,多项式中不含xy项。
七、课后反思。
课题:整式的加减(2)--- 去括号 课型:新课 课时:1课时
【教学目标】
1.理解去括号时符号变化的规律,会用去括号法则进行计算.
2.通过类比,让我们经历去括号法则的探索过程,掌握去括号的方法.
3.通过观察、猜想、整理,培养我们的归纳能力;通过合作学习、讨论,培养我们学会与他人交流的意识和能力.
【重点难点】
重点:
难点:
【导引自学】
1. 在格尔木到拉萨路段,如果列车通过冻土地段要t小时,那么它通过非冻土地段的时间为(t-0.5)小时,于是,冻土地段的路程为100t千米,非冻土地段的路程为120(t-0.5)千米,因此,这段铁路全长为(单位:㎞):
冻土地段与非冻土地段相差(单位:㎞):
2.乘法分配律如何用字母表示?
3.利用乘法分配律计算:
12×(+)= —12×(-)=
2×(x+8)= -3(3x+4)= -7(7y-5)=
4.通过刚才的计算,你能够发现去括号时符号的变化规律吗?项数呢?你明白它们变化的依据吗?
【双基自测】
计算:
⑴ 2(4x-0.5) ⑵-3(1-x) ⑶-x+(2x-2)-(3x+5)
⑷3a +a-(2 a -2a) +(3a-a) ⑸ (5a+4b+7c)-(5c-3b-6a)
⑹ (8xy-x+y)-(x-y+8xy) ⑺(2 x-+3x) -4(x-x+)
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
去括号法则:
(1)、如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
(2)、如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
特别地,+(x-3)与-(x-3)可以分别看作1与-1分别乘(x-3).
+(x-3)=x-3 (括号没了,括号内的每一项都没有变号)
-(x-3)=-x+3 (括号没了,括号内的每一项都改变了符号)
注意事项
(1)去括号规律要准确理解,去括号应对括号的每一项的符号都予考虑,做到要变都变;要不变,则谁也不变;
(2)括号内原有几项去掉括号后仍有几项.
三、范例剖析,合作探究。
例1.化简下列各式:
(1)8a+2b+(5a-b); (2)(5a-3b)-3(a2-2b).
例2:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50㎞/h,水流速度是a㎞/h。
(1)2h后两船相距多远?
(2)2h后甲船比乙船多航行多少千米?
四、课堂反馈,达标测评。
1、判断:下列去括号有没有错误?若有错,请改正:
(1) a2-(2a-b+c)=a2-2a-b+c; (2) -(x-y)+(xy-1)=-x-y+xy-1.
2、去括号-[a-(b-c)].
3、先去括号,再合并同类项:
(1)(2x-3y)+(5x+4y); (2) (8a-7b)-(4a-5b);
(3)a-(2a+b) -2(a-2b); (4)3(5x+4)-(3x-5);
(5)(8x-3y)-(4x+3y-z)+2z; (6)2-(1+x)+(1+x+x2-x2);
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、根据去括号法则,在横线上填上“+”或“-”
(1)
(2)
(3)
(4)
2、化简:
3、数在数轴上的位置如图所示,化简:
4、化简的最后结果是( )
A. B. C. D.
5、下列去括号中正确的是( )
A. B.
C. D.
6、已知,那么的值为( )
A.80 B.10 C.210 D.40
7、减去等于的代数式是( )
A. B. C. D.
8、化简:
(1) (2)
七、课后反思。
课题:整式加减(3 )——化简求值 课型:新课 课时:1课时
【教学目标】
1.让学生从实际背景中去体会进行整式的加减的必要性,并能灵活运用整式的加减的步骤进行运算。
2.掌握整式的化简求值题解题步骤与方法
3.培养学生审题、分析、归纳、总结以及概括能力。养成仔细、严谨数学解题习惯。
【重点难点】
重点:准确进行整式加减运算
难点:准确进行整式加减运算
【导引自学】
去括号法则是什么?试举两例加以说明。
式子-7.5+3.16+-15两种读法是什么?
3.下列式子可以看着哪两个整式的和(或差)?如何化简?
(1)(x+y)—(2x-3y) (2)2
整式加减的一般步骤是什么?
【双基自测】
计算:
(1)3xy—4xy—(—2xy); (2)—ab—a+ a—(—ab)
(3)(-x+2x+5)+(4x-3-6x) (4)(3a-ab+7)-(-4a+2ab+7)
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
整式加减的一般步骤可以总结为:
(1)如果有括号,那么先去括号。(去括号时要认真检查符号和项数)
(2)如果有同类项,再合并同类项。
三、范例剖析,合作探究。
例1: 求 x-2(x-y2)+(-x+y2)的值,其中x=-2,y=
例2:已知多项式A=4a2+5b,B=-3a2-2b,计算2A-B的结果
四、课堂反馈,达标测评。
1.先化简,再求值
2.
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、化简:(1)(x+y)—(2x-3y) (2)2
(3)―2y3+(3xy2―x2y)―2(xy2―y3) (5)
(6)
2、求整式x2―7x―2与―2x2+4x―1的差。
3、化简求值:(2x3―xyz)―2(x3―y3+xyz)+(xyz―2y3),其中x=1,y=2,z=―3。
4、一个多项式加上2x2-x3-5-3x4得3x4-5x3-3,求这个多项式。
5、已知A+B=3x2-5x+1,A-C=-2x+3x2-5,当x=2时,求B+C的值。
6、如果多项式8x2-3x+5与多项式3x2+4mx2-5x+3相加后不含x2项,求m的值。
7、小文在计算某多项式减去的差时,误认为是加上,求得答案是。
(1)求这个多项式。(2)正确答案是多少?
10.若多项式
的值与无关,求的值。
6、各位数字是a,十位数字是b,百位数字是c的三位数与把该三位数的个位数字与百位数字对调位置后所得的三位数的差为 。
七、课后反思。
课题:整式的加减(4)——实际问题 课型:新课 课时:1课时
【教学目标】
1、通过实际问题列代数式并运用整式加减法则进行运算。
2、通过小组合作,准确理解题意,正确列出式子和计算出结果。
3、培养细心、耐心的数学素养,加强学生计算能力,进而提高学生学数学的兴趣。
【重点难点】
重点:通过实际问题正确列出式子和计算出结果。
难点:通过实际问题正确列出式子和计算出结果。
【导引自学】
什么是同类项?合并同类项的法则是什么?
怎样去括号?去括号法则是什么?
整式加减的一般步骤是什么?
4. 某学生合唱团出场时第一排站了n名,从第二排起每一排都比前一排多一人。
(1) 一共站了四排,则该合唱团一共有多少名学生参加?
(2) 一共站了m排,则该合唱团一共有多少名学生参加?
通过此例,在解决实际问题时我们如何正确得出结果?
【双基自测】
1. 一种笔记本的单价是x元,圆珠笔的单价是y元,小红买这种笔记本3本,买圆珠笔2支;小明买这种笔记本4本,买圆珠笔3支。买这些笔记本和圆珠笔,小红和小明一共花费多少钱?
2. 做大小两个长方形纸盒,尺寸如下(单位:cm):
长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c
做这两个纸盒共用料多少平方厘米?
(2) 做大纸盒比做小纸盒多用料多少平方厘米?
【导引教学】
一、检查预习,小组互助。
二、小组学习,教师视导。
引导学生,在解决实际问题时,要明确:
(1)认真审题,题目告诉了什么。要解决问题必须知道什么。
(2)学会分步骤解题,每一步必须弄得清清楚楚,不要一步写出综合算式
切忌题目没有读懂,盲目写过程,写了改,改了写。心情急躁、没有耐心、不细心的人学不好数学
三、范例剖析,合作探究。
例1:某地电话拨号上网有了两种收费方式,用户可以任取其一:
(A)计时制:0.05元/分;
(B)包月制:50元/月(只限一部宅电上网),此外,每种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网时间为x小时,请你写出每种收费方式下该用户应该支付的费用。
(2)若某用户估计一个月内上网时间为20h,你认为采用哪种方式合算。
例2:(1)任意写两位数; (2)交换这个两位数的十位数字和个位数字,又得到一个两位数;
(3)求这两个数的和。
再写几个两位数按上面的过程试一试,这些和有什么规律?
你能证明你的猜想吗?
四、课堂反馈,达标测评。
1、A和B两家公司都准备向社会招聘人才,两家公司招聘条件基本相同,只有工资待遇有如下差异:A公司年薪10000元,每年加工龄工资50元,B公司半年年薪5000元,每半年家工龄工资50元,从经济收入的角度考虑,选择哪家公司有利?
2、(1)任意写一个三位数;(2)交换它的百位数字与个位数字,又得到一个数两个数相减;
(3)两个数相减后的结果有什么规律,这个规律对任意一个三位数都成立吗?
五、课堂小结,学生总结学习内容,交流收获、困惑与反思。
六、布置课后作业和预习案。
1、学校计划修建一个如图1所示的喷水池,但由于占地太多,需改建如图2的形状,且外圆直径不变,只是担心原来备好的材料不够。
(1)请你比较两种方案,哪一种需用的材料多(即比较哪个周长更长)?
(2)由以上结论,请推测:若题目中的三个小圆改为n个小圆,结论是否不变?那么现在要在外圆内修四个小圆,结果怎样?
七、课后反思。
