2021-2022学年人教版七年级数学下册8.3实际问题与二元一次方程组(和差倍分问题、表格或图示信息问题)课后练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册8.3实际问题与二元一次方程组(和差倍分问题、表格或图示信息问题)课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 117.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 14:21:46 | ||
图片预览


文档简介
2021-2022学年人教版七年级数学下册 第八章 二元一次方程组 8.3 实际问题与二元一次方程组(和差倍分问题、表格或图示信息问题) 课后练习
一、选择题
1.小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n倍”;小玲对小倩说:“你若给我n元,我的钱数将是你的2倍”,其中n为正整数,则n的可能值的个数是( ).
A.1 B.2 C.3 D.4
2.甲、乙两人各买了相同数量的信封和信笺,甲每发出一封信只用1张信笺,乙每发出一封信用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封,则甲、乙两人买的信笺张数、信封个数分别为( )
A.150,100 B.125,75 C.120,70 D.100,150
3.为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,所列方程组正确的是( )
A. B. C. D.
4.一些2分与5分的硬币共299分,其中2分的个数是5分个数的4倍,5分的有________个.
A.22 B.23 C.24 D.25
5.楠溪江某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有张成人票,张儿童票,根据题意,下列方程组正确的是【 】
A. B. C. D.
6.如图,由组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行(横) 每一列(竖)以及每一条对角线(斜)上的三个代数式的和均相等,则方格中“a”的数是( )
y a
9 11
A.6 B.7 C.8 D.9
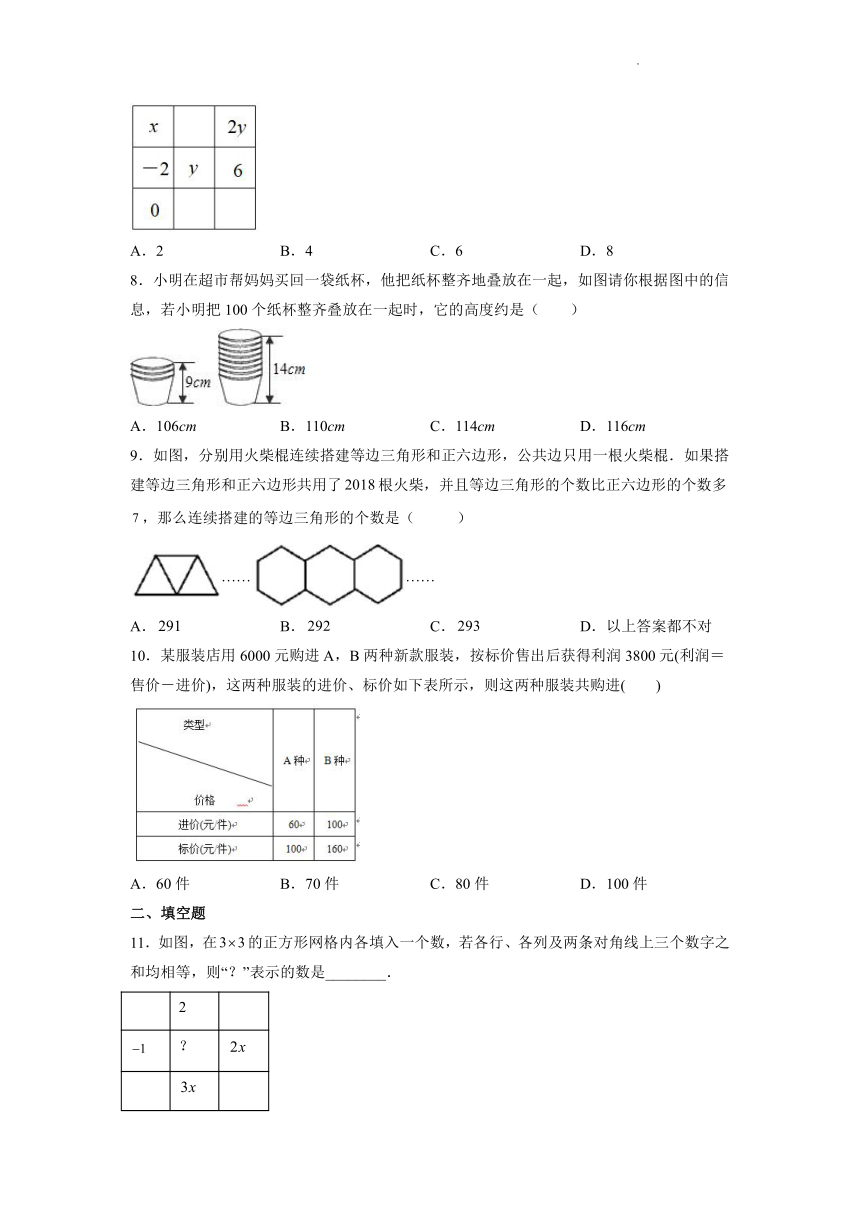
7.在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )
A.2 B.4 C.6 D.8
8.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )
A.106cm B.110cm C.114cm D.116cm
9.如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了根火柴,并且等边三角形的个数比正六边形的个数多,那么连续搭建的等边三角形的个数是( )
…………
A. B. C. D.以上答案都不对
10.某服装店用6000元购进A,B两种新款服装,按标价售出后获得利润3800元(利润=售价-进价),这两种服装的进价、标价如下表所示,则这两种服装共购进( )
A.60件 B.70件 C.80件 D.100件
二、填空题
11.如图,在的正方形网格内各填入一个数,若各行、各列及两条对角线上三个数字之和均相等,则“?”表示的数是________.
2
?
12.如图,长方形中,放置个形状、大小都相同的小长方形,根据图中所给的数据,可得图中小长方形的面积为__________.
13.《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为_______ 钱
14.在等式5×□+3×△=4的□和△处分别填入一个数,使这两个数是互为相反数,则□= __.
15.有两个有理数,其和为1,其差为5,则其积为__________.
三、解答题
16.某班为充实图书角图书,在学习委员的倡议下进行了一次给班级捐书活动,受污染区域(阴影部分)记录了在相应捐书数目为N时的人数分布情况.
捐书数N 1 2 3 4 5 6
捐书N本的人数 1 2 17 ■ ■ 4
已知捐书4本或4本以上的人平均每人捐书4.7本,捐书5本以及5本以下的同学平均捐书3.5本.问捐书4本和5本的各有多少人?
17.在数学社会实践活动中,某校七年级(3)班为了调查A,B,C三个超市哪个最受欢迎,分成甲,乙,丙三个实践活动小组在同一时间调查了A,B,C三家超市的人流量(某时段进入超市的人数).三个实践小组分别汇报了所调查超市的人流量.
甲组同学说:“A超市在该时段人流量为2000人”;
乙组同学说:“B超市在该时段人流量比C超市在该时段少150人”;
丙组同学说:“C超市在该时段人流量的2倍与B超市在该时段人流量的差与A超市在该时段的人流量相同”.请求出B超市和C超市在该时段人流量为多少?
18.某校准备组织七年级学生参加夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人,用一辆小客车和2辆大客车每次可运送学生110人;现有学生400人,计划租用小客车辆,大客车辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可运送多少学生?
(2)请你帮学校设计出所有的租车方案.
19.为迎接“国家卫生城市”复检,某校准备购买可回收垃圾和其余垃圾两种型号的垃圾箱,通过市场调研得知:购买3个可回收垃圾箱和2个其余垃圾箱共需490元,购买2个可回收垃圾箱比购买3个其余垃圾箱少用150元.
(1)求每个可回收垃圾箱和其余垃圾箱各多少元?
(2)该校现需要购买可回收垃圾箱16个,其余垃圾箱14个,共需花费多少元?
20.为了让居民树立起“节约水,保护水”的用水概念,某市的居民生活用水按阶梯式水价计费,下表是该市居民“一户一表”生活用水计费价格表的部分信息.
每户每月用水量 自来水销售价格/(元/t) 污水处理价格/(元/t)
10t及以下 m 0.8
超过10t但不超过20t的部分 n 0.8
超过20t的部分 3.20 0.8
(说明:①每户产生的污水量等于该用户自来水用量:②水费=自来水费用+污水处理费用)
已知小李家去年6月份用水10t,缴纳水费25元;7月份用水15t,缴纳水费45.5元.
(1)求表中的m,n的值;
(2)小李家去年8月份的水费正好是家庭月收入的1%,己知小李家的月收入为8000元,求小李家8月份的用水量.
21.一批货物要运往A地,货主准备租用汽车运输公司的甲、乙两种货车,已知前两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车辆数(辆) 2 3
乙种货车辆数(辆) 3 6
累计运送货物(吨) 15.5 27
根据表格提供数据,请解答以下问题:
(1)甲、乙两种货车每辆一次分别运送多少吨货物?
(2)该货主租用以上甲种货车4辆、乙种货车8辆,一次性刚好运往完这批货物,如果按每吨付运费30元计算,问货主携带1000元现金是否够支付?
22.小明在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购买 6 5 980
第二次购买 3 6 840
第三次购买 9 8 760
(1)小明以折扣价购买商品A、B是第 次购物;
(2)求商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
23.某电器超市销售每台进价为80元、220元的两种型号的电风扇,如表所示是六月份前2周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
销售时段 销售数量 销售收入
种型号 种型号
第一周 6 5 2220元
第二周 4 10 3480元
(1)求两种型号的电风扇的销售单价;
(2)若超市一共采购这两种型号的电风扇共120台,售完后该超市能否实现利润为10000元的目标 若能,请给出相应的采购方案;若不能,请说明理由;
(3)锦绣育才教育集团花费1620元在该超市购进两种型号的电风扇,请问有几种不同的购买方案 请说明理由.
【参考答案】
1.D 2.A 3.D 4.B 5.B 6.B 7.C 8.A 9.C 10.C
11.
12.33
13.150
14.2
15.
16.捐书4本的有10人,捐书5本的有6人.
17.超市1700人,超市1850人
18.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生;(2)租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆:③小客车2辆,大客车8辆
19.(1)每个可回收垃圾箱90元,每个其余垃圾箱110元;(2)2980元
20.(1)m=1.7,n=3.3;(2)23.5吨
21.(1)甲种货车每辆一次运送4吨货物,乙种货车每辆一次运送2.5吨货物.(2)不够支付.
22.(1)三;(2)A、B两种商品的标价分别为80元,100元;(3)商店是打5折出售商品A、B的
23.(1)A种型号的电风扇的销售单价为120元,B种型号的电风扇的销售单价为300元;(2)不能;(3)3种
一、选择题
1.小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n倍”;小玲对小倩说:“你若给我n元,我的钱数将是你的2倍”,其中n为正整数,则n的可能值的个数是( ).
A.1 B.2 C.3 D.4
2.甲、乙两人各买了相同数量的信封和信笺,甲每发出一封信只用1张信笺,乙每发出一封信用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封,则甲、乙两人买的信笺张数、信封个数分别为( )
A.150,100 B.125,75 C.120,70 D.100,150
3.为了绿化校园,30名学生共种78棵树苗,其中男生每人种3棵,女生每人种2棵,设男生有x人,女生有y人,根据题意,所列方程组正确的是( )
A. B. C. D.
4.一些2分与5分的硬币共299分,其中2分的个数是5分个数的4倍,5分的有________个.
A.22 B.23 C.24 D.25
5.楠溪江某景点门票价格:成人票每张70元,儿童票每张35元.小明买20张门票共花了1225元,设其中有张成人票,张儿童票,根据题意,下列方程组正确的是【 】
A. B. C. D.
6.如图,由组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行(横) 每一列(竖)以及每一条对角线(斜)上的三个代数式的和均相等,则方格中“a”的数是( )
y a
9 11
A.6 B.7 C.8 D.9
7.在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )
A.2 B.4 C.6 D.8
8.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )
A.106cm B.110cm C.114cm D.116cm
9.如图,分别用火柴棍连续搭建等边三角形和正六边形,公共边只用一根火柴棍.如果搭建等边三角形和正六边形共用了根火柴,并且等边三角形的个数比正六边形的个数多,那么连续搭建的等边三角形的个数是( )
…………
A. B. C. D.以上答案都不对
10.某服装店用6000元购进A,B两种新款服装,按标价售出后获得利润3800元(利润=售价-进价),这两种服装的进价、标价如下表所示,则这两种服装共购进( )
A.60件 B.70件 C.80件 D.100件
二、填空题
11.如图,在的正方形网格内各填入一个数,若各行、各列及两条对角线上三个数字之和均相等,则“?”表示的数是________.
2
?
12.如图,长方形中,放置个形状、大小都相同的小长方形,根据图中所给的数据,可得图中小长方形的面积为__________.
13.《九章算术》中记载“今有共买羊,人出五,不足四十五;人出七,不足三,问人数、羊价各几何?”其大意是:今有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱,问合伙人数、羊价各是多少?此问题中羊价为_______ 钱
14.在等式5×□+3×△=4的□和△处分别填入一个数,使这两个数是互为相反数,则□= __.
15.有两个有理数,其和为1,其差为5,则其积为__________.
三、解答题
16.某班为充实图书角图书,在学习委员的倡议下进行了一次给班级捐书活动,受污染区域(阴影部分)记录了在相应捐书数目为N时的人数分布情况.
捐书数N 1 2 3 4 5 6
捐书N本的人数 1 2 17 ■ ■ 4
已知捐书4本或4本以上的人平均每人捐书4.7本,捐书5本以及5本以下的同学平均捐书3.5本.问捐书4本和5本的各有多少人?
17.在数学社会实践活动中,某校七年级(3)班为了调查A,B,C三个超市哪个最受欢迎,分成甲,乙,丙三个实践活动小组在同一时间调查了A,B,C三家超市的人流量(某时段进入超市的人数).三个实践小组分别汇报了所调查超市的人流量.
甲组同学说:“A超市在该时段人流量为2000人”;
乙组同学说:“B超市在该时段人流量比C超市在该时段少150人”;
丙组同学说:“C超市在该时段人流量的2倍与B超市在该时段人流量的差与A超市在该时段的人流量相同”.请求出B超市和C超市在该时段人流量为多少?
18.某校准备组织七年级学生参加夏令营,已知用3辆小客车和1辆大客车每次可运送学生105人,用一辆小客车和2辆大客车每次可运送学生110人;现有学生400人,计划租用小客车辆,大客车辆,一次送完,且恰好每辆车都坐满.
(1)1辆小客车和1辆大客车都坐满后一次可运送多少学生?
(2)请你帮学校设计出所有的租车方案.
19.为迎接“国家卫生城市”复检,某校准备购买可回收垃圾和其余垃圾两种型号的垃圾箱,通过市场调研得知:购买3个可回收垃圾箱和2个其余垃圾箱共需490元,购买2个可回收垃圾箱比购买3个其余垃圾箱少用150元.
(1)求每个可回收垃圾箱和其余垃圾箱各多少元?
(2)该校现需要购买可回收垃圾箱16个,其余垃圾箱14个,共需花费多少元?
20.为了让居民树立起“节约水,保护水”的用水概念,某市的居民生活用水按阶梯式水价计费,下表是该市居民“一户一表”生活用水计费价格表的部分信息.
每户每月用水量 自来水销售价格/(元/t) 污水处理价格/(元/t)
10t及以下 m 0.8
超过10t但不超过20t的部分 n 0.8
超过20t的部分 3.20 0.8
(说明:①每户产生的污水量等于该用户自来水用量:②水费=自来水费用+污水处理费用)
已知小李家去年6月份用水10t,缴纳水费25元;7月份用水15t,缴纳水费45.5元.
(1)求表中的m,n的值;
(2)小李家去年8月份的水费正好是家庭月收入的1%,己知小李家的月收入为8000元,求小李家8月份的用水量.
21.一批货物要运往A地,货主准备租用汽车运输公司的甲、乙两种货车,已知前两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车辆数(辆) 2 3
乙种货车辆数(辆) 3 6
累计运送货物(吨) 15.5 27
根据表格提供数据,请解答以下问题:
(1)甲、乙两种货车每辆一次分别运送多少吨货物?
(2)该货主租用以上甲种货车4辆、乙种货车8辆,一次性刚好运往完这批货物,如果按每吨付运费30元计算,问货主携带1000元现金是否够支付?
22.小明在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购买 6 5 980
第二次购买 3 6 840
第三次购买 9 8 760
(1)小明以折扣价购买商品A、B是第 次购物;
(2)求商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
23.某电器超市销售每台进价为80元、220元的两种型号的电风扇,如表所示是六月份前2周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
销售时段 销售数量 销售收入
种型号 种型号
第一周 6 5 2220元
第二周 4 10 3480元
(1)求两种型号的电风扇的销售单价;
(2)若超市一共采购这两种型号的电风扇共120台,售完后该超市能否实现利润为10000元的目标 若能,请给出相应的采购方案;若不能,请说明理由;
(3)锦绣育才教育集团花费1620元在该超市购进两种型号的电风扇,请问有几种不同的购买方案 请说明理由.
【参考答案】
1.D 2.A 3.D 4.B 5.B 6.B 7.C 8.A 9.C 10.C
11.
12.33
13.150
14.2
15.
16.捐书4本的有10人,捐书5本的有6人.
17.超市1700人,超市1850人
18.(1)1辆小客车和1辆大客车都坐满后一次可送65名学生;(2)租车方案有3种,①小客车20辆,大客车0辆;②小客车11辆,大客车4辆:③小客车2辆,大客车8辆
19.(1)每个可回收垃圾箱90元,每个其余垃圾箱110元;(2)2980元
20.(1)m=1.7,n=3.3;(2)23.5吨
21.(1)甲种货车每辆一次运送4吨货物,乙种货车每辆一次运送2.5吨货物.(2)不够支付.
22.(1)三;(2)A、B两种商品的标价分别为80元,100元;(3)商店是打5折出售商品A、B的
23.(1)A种型号的电风扇的销售单价为120元,B种型号的电风扇的销售单价为300元;(2)不能;(3)3种
