2021-2022学年人教版八年级数学下册18.2特殊平行四边形分类训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2特殊平行四边形分类训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 345.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学下册《18-2特殊平行四边形》知识点分类训练(附答案)
一.直角三角形斜边上的中线
1.直角三角形斜边上的高与中线分别是5和6,则它的面积是( )
A.60 B.50 C.40 D.30
二.矩形的判定
2.若O是四边形ABCD对角线的交点且OA=OB=OC=OD,则四边形ABCD是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
3.如图,已知平行四边形ABCD的对角线AC,BD相交于点O,下列选项能使平行四边形ABCD成为矩形的条件是( )
A.AB=AD B.∠AOB=60° C.AC⊥BD D.∠OBC=∠OCB
三.矩形的性质
4.已知矩形的对角线为1,面积为m,则矩形的周长为( )
A. B. C.2 D.2
5.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10 B.8 C.6 D.4
6.如图,在矩形ABCD中,AB=9,AD=12,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则ED的长为( )
A. B. C.2 D.
7.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为 .
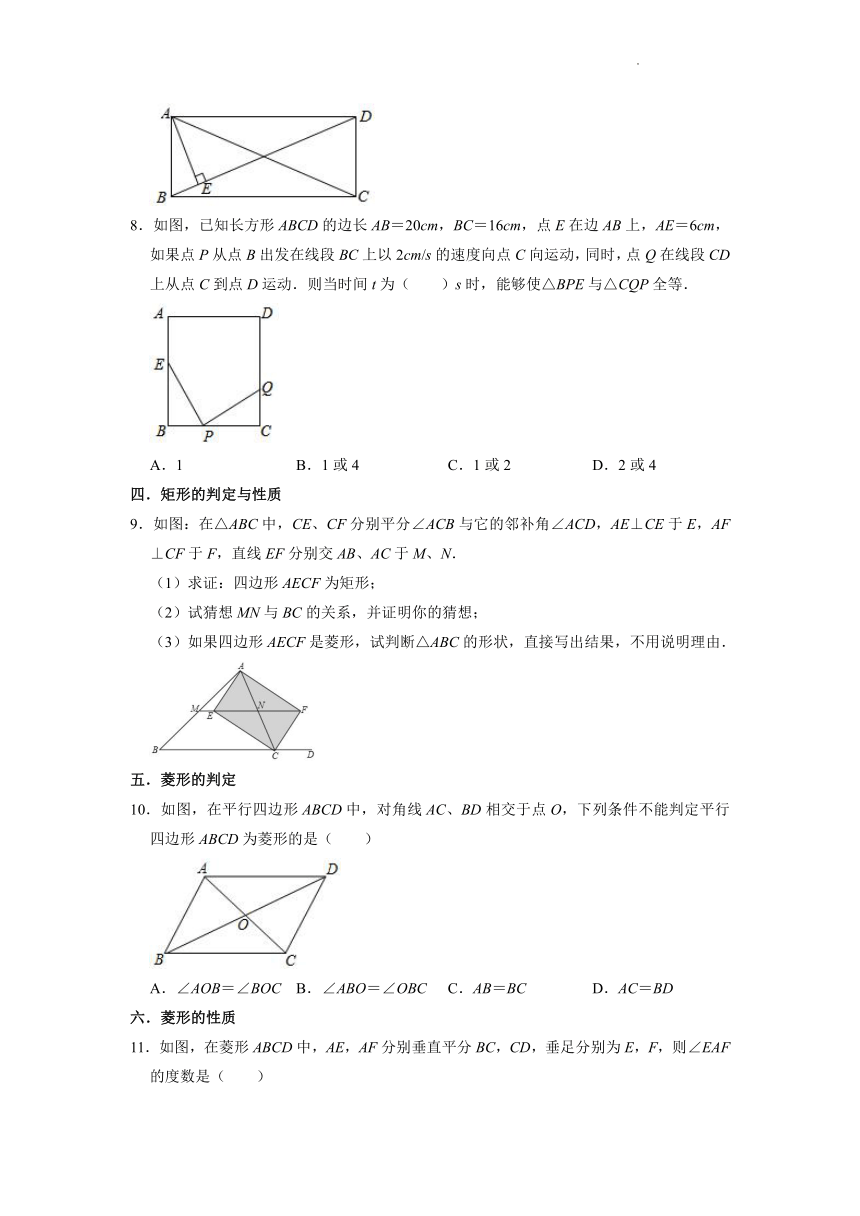
8.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A.1 B.1或4 C.1或2 D.2或4
四.矩形的判定与性质
9.如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
五.菱形的判定
10.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为菱形的是( )
A.∠AOB=∠BOC B.∠ABO=∠OBC C.AB=BC D.AC=BD
六.菱形的性质
11.如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是( )
A.30° B.45° C.60° D.90°
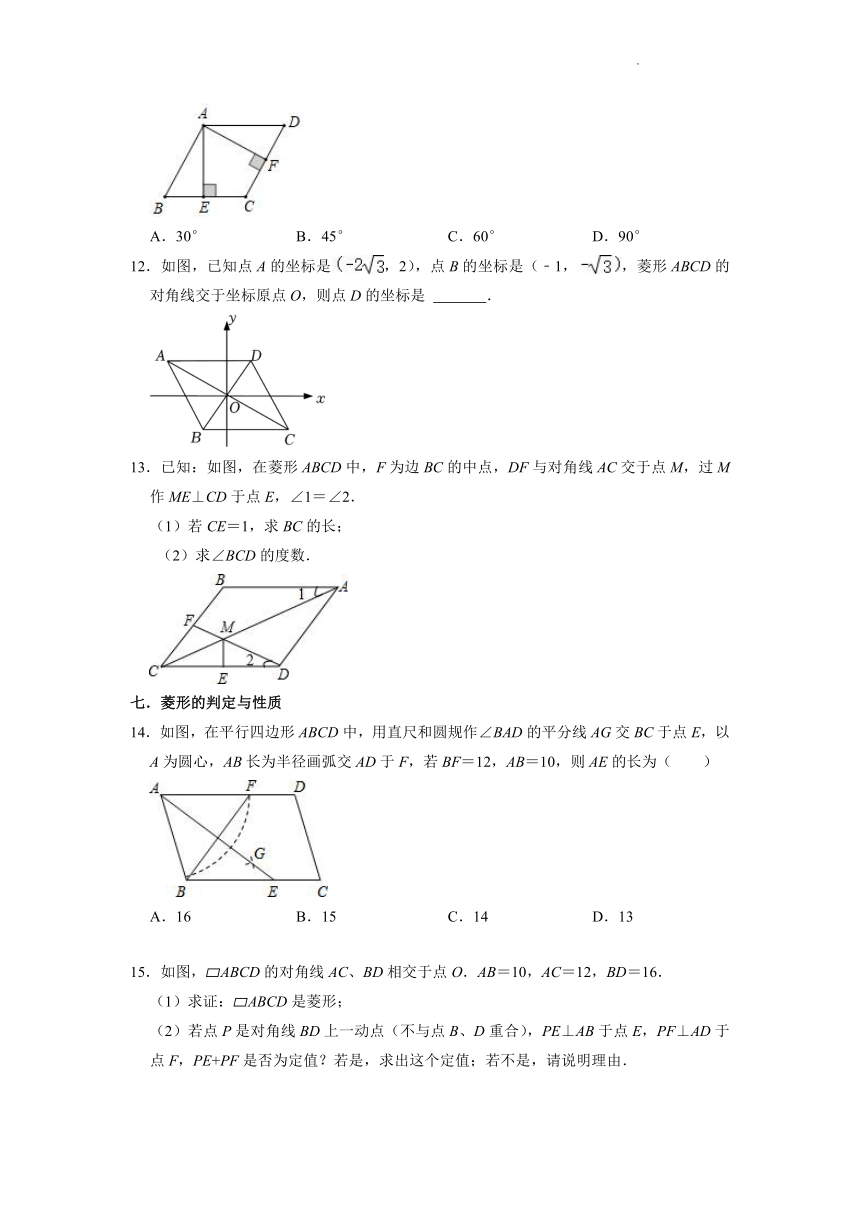
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求∠BCD的度数.
七.菱形的判定与性质
14.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
15.如图, ABCD的对角线AC、BD相交于点O.AB=10,AC=12,BD=16.
(1)求证: ABCD是菱形;
(2)若点P是对角线BD上一动点(不与点B、D重合),PE⊥AB于点E,PF⊥AD于点F,PE+PF是否为定值?若是,求出这个定值;若不是,请说明理由.
八.正方形的判定
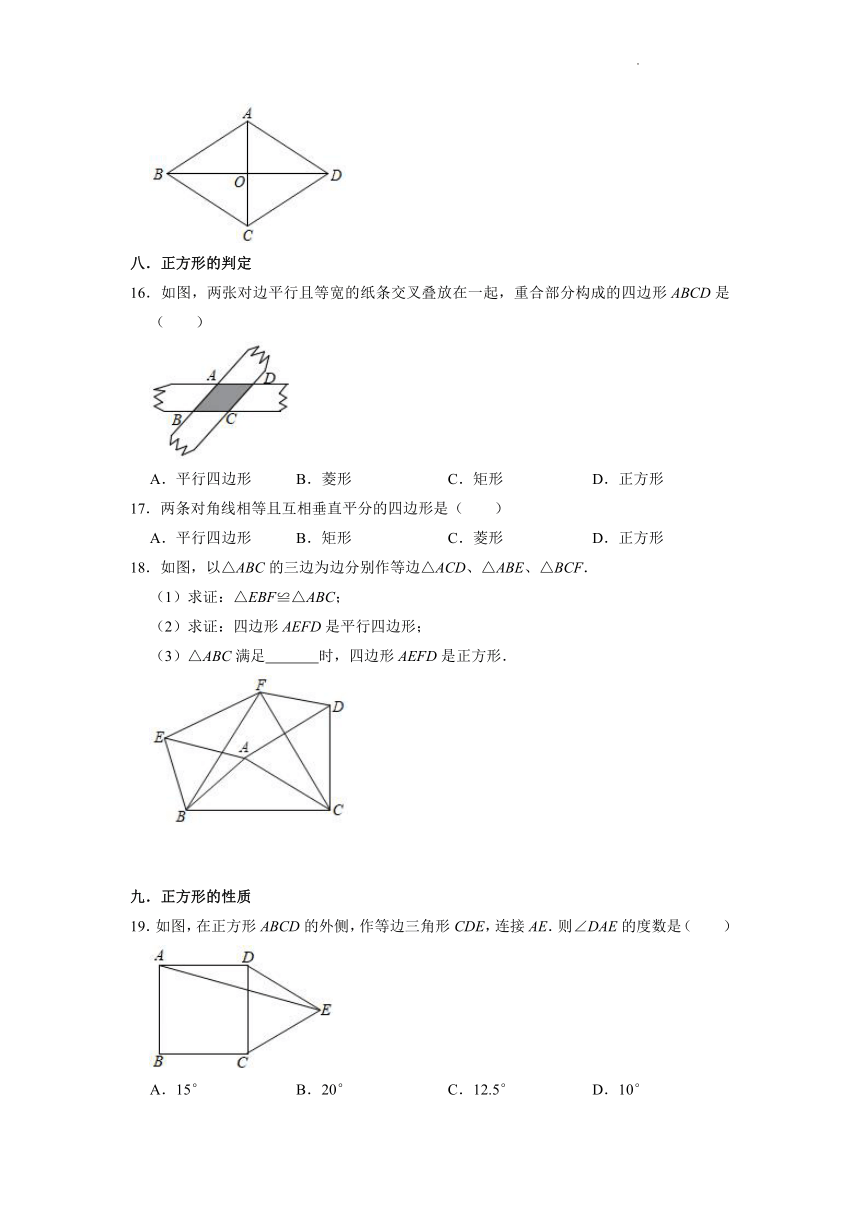
16.如图,两张对边平行且等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
17.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
18.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF.
(1)求证:△EBF≌△ABC;
(2)求证:四边形AEFD是平行四边形;
(3)△ABC满足 时,四边形AEFD是正方形.
九.正方形的性质
19.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是( )
A.15° B.20° C.12.5° D.10°
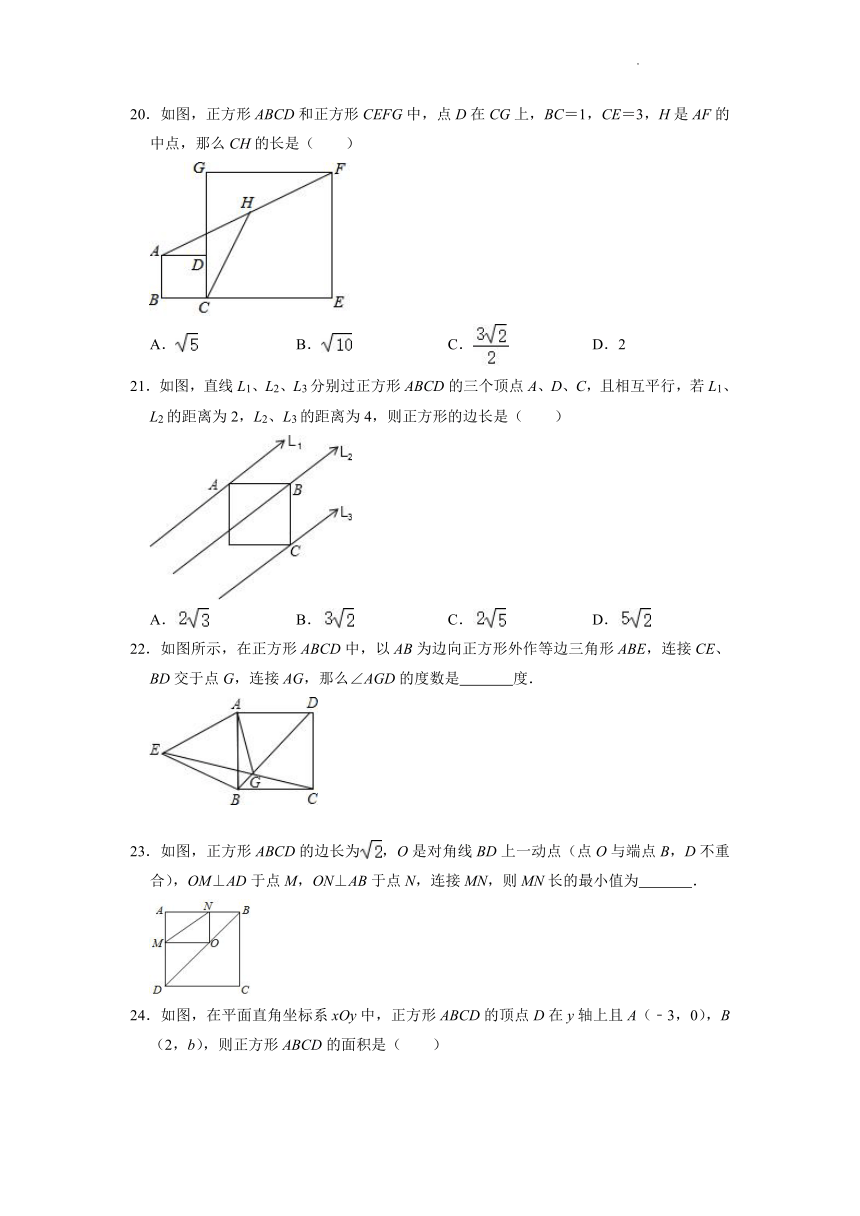
20.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. B. C. D.2
21.如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为2,L2、L3的距离为4,则正方形的边长是( )
A. B. C. D.
22.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
23.如图,正方形ABCD的边长为,O是对角线BD上一动点(点O与端点B,D不重合),OM⊥AD于点M,ON⊥AB于点N,连接MN,则MN长的最小值为 .
24.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
25.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.
(1)求证:BG=CE;
(2)求证:CE⊥BG;
(3)求:∠AME的度数.
26.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
27.如图,点E是正方形ABCD外一点,连接AE、BE和DE,过点A作AE垂线交DE于点P.若AE=AP=2,PB=6.下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为2;④S正方形ABCD=32+4.则正确结论的个数是( )
A.1 B.2 C.3 D.4
28.如图,已知四边形ABCD是正方形,对角线AC、BD相交于O.
(1)如图1,设E、F分别是AD、AB上的点,且∠EOF=90°,线段AF、BF和EF之间存在一定的数量关系.请你用等式直接写出这个数量关系;
(2)如图2,设E、F分别是AB上不同的两个点,且∠EOF=45°,请你用等式表示线段AE、BF和EF之间的数量关系,并证明.
29.如图①,正方形ABCD中,M是AB的中点,E是延长线上一点.MN⊥DM,且交∠CBE的平分线于N.
(1)若点F是AD的中点,求证:MD=MN;
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”,其它条件不变.如图②所示,则结论“MD=MN”是否成立.若成立,给出证明;若不成立,请说明理由.
30.如图,已知在△ABC中,∠A是钝角,以AB为边作正方形ABDE,使△ABC正方形ABDE分居在AB两侧,以AC为边作正方形ACFG,使△ABC正方形ACFG分居在AC两侧,BG与CE交于点M,连接AM.
(1)求证:BG=CE;
(2)求:∠AMC的度数;
(3)若BG=a,MG=b,ME=c,求:S△ABM:S△ACM(结果可用含有a,b,c的式子表示).
31.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
十.正方形的判定与性质
32.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是( )
A.②③ B.②④ C.①③④ D.②③
参考答案
一.直角三角形斜边上的中线
1.解:∵直角三角形斜边上的中线CD是6,
∴斜边AB长为:2×CD=6×2=12,
∴它的面积=×AB×CE=×12×5=30,
故选:D.
二.矩形的判定
2.解:∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形.
故选:B.
3.解:A、∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、由四边形ABCD是平行四边形,∠AOB=60°,不能判定平行四边形ABCD为矩形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项D符合题意;
故选:D.
三.矩形的性质
4.解:设矩形的长、宽分别为a、b,
∵矩形的对角线为1,面积为m,
∴a +b =1,ab=m,
∴a+b===,
∴矩形的周长为2(a+b)=2,
故选:C.
5.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE==8.
故选:B.
6.解:连接EC,如图,
∵四边形ABCD是矩形,
∴AO=OC.
∵EO⊥AC,
∴OE为线段AC的垂直平分线.
∴EC=AE.
设DE=x,则AE=12﹣x.
∴EC=12﹣x,
在Rt△ECD中,
∵EC2=DE2+DC2,
∴(12﹣x)2=x2+92.
解得:x=.
∴DE=.
故选:A.
7.解:∵四边形ABCD是矩形,AC、BD是矩形的对角线且相交于O,
∴OA=OB,
∴∠BAC=∠ABD,
∵∠DAE=3∠BAE,∠DAE+∠BAE=90°,
∴∠BAE=22.5°,∠DAE=67.5°.
∵在矩形ABCD,∠DAE+∠ADB=90°,∠ADB+∠ABD=90°,
∴∠ABD=∠DAE=67.5°,即∠BAC=∠ABD=67.5°,
∴∠EAC=∠BAC﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
8.解:分两种情况:
①当EB=PC,BP=QC时,△BPE≌△CQP,
∵AB=20cm,AE=6cm,
∴EB=14cm,
∴PC=14cm,
∵BC=16cm,
∴BP=2cm,
∵点P从点B出发在线段BC上以2cm/s的速度向点C运动,
∴t=2÷2=1(s);
②当BP=CP,BE=QC时,△BEP≌△CQP,
由题意得:2t=16﹣2t,
解得:t=4(s),
故选:B.
四.矩形的判定与性质
9.(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=(∠BCE+∠ACE+∠ACF+∠DCF)=×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN=BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
五.菱形的判定
10.解:A、∵∠AOB=∠BOC,∠AOB+∠BOC=180°,
∴∠AOB=∠BOC=90°,
∴AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、过O作OE⊥AB于E,OF⊥BC于F,如图所示:
∵∠ABO=∠OBC,
∴OE=OF,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴△AOB的面积=△COB的面积,
又∵△AOB的面积=AB×OE,△COB的面积=BC×OF,
∴AB×OE=BC×OF,
∴AB=BC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵平行四边形ABCD中,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵平行四边形ABCD中,AC=BD,
∴平行四边形ABCD是矩形,故选项D符合题意;
故选:D.
六.菱形的性质
11.解:连接AC,如图:
∵AE,AF分别垂直平分BC,CD,
∴AB=AC,AD=AC,∠AEC=∠AFC=90°,
又∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴AB=AC=BC=AD=CD,
∴△ABC、△ACD是等边三角形,
∴∠B=∠ACB=∠ACD=60°,
∴∠BCD=120°,
∴在四边形AECF中,∠EAF=360°﹣90°﹣90°﹣120°=60°.
故选:C.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.解:(1)∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴CM=DM,
∵ME⊥CD,
∴CE=DE=CD=1,
∴BC=CD=2;
(2)连接BD,
∵四边形ABCD是菱形,
∴CB=CD,∠ACB=∠ACD,
∵F为边BC的中点,
∴CF=CB,
∵CE=CD,
∴CE=CF,
在△MCF和△NCE中
∴△FCM≌△ECM(SAS),
∴∠CFM=∠CEM=90°,
∴DF⊥BC,
∴BD=CD,
∴BC=CD=BC,
∴△BCD是等边三角形,
∴∠BCD=60°.
七.菱形的判定与性质
14.解:连接EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA===8,
∴AE=2OA=16.
故选:A.
15.(1)证明:∵四边形ABCD是平行四边形,AC=12,BD=16,AB=10,
∴AO=CO=AC=6,BO=DO=BD=8,
∵62+82=102,
∴AO2+BO2=AB2,
∴∠AOB=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:是定值,
连接AP,过B作BH⊥DA于H,
∵四边形ABCD是菱形,
∴AB=AD=10,S△ABD=S菱形ABCD=×AC BD=×12×16=48,
∵S△ABD=S△ABO+S△ADO=AB PE+AD PF=AD(PE+PF)=AD BH,
∴PE+PF=BH,
∵S△ABD=AD BH=×10 BH=48,
∴BH=,
∴PE+PF=.
故PE+PF定值为.
八.正方形的判定
16.解:由图可知,过A点作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相等,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵SABCD=BC×AE=CD AF.
又∵AE=AF,
∴BC=CD,
∴四边形ABCD为菱形.
故选:B.
17.解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
18.(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,
即∠CBA=∠FBE,
在△EBF和△ABC中,
,
∴△EBF≌△ABC(SAS);
(2)证明:∵△EBF≌△ABC,
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴AB=AE=DF,
∴四边形AEFD是平行四边形;
(3)解:当AB=AC,∠BAC=150°时,四边形ADEF是正方形.
理由是:∵△ABE、△ACD为等边三角形,
∴AB=AE,AC=AD,∠EAB=∠DAC=60°,
∵AB=AC,
∴AE=AD,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∵∠BAC=150°,
∴∠EAD=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形ADEF是正方形,
故答案为:AB=AC,∠BAC=150°.
九.正方形的性质
19.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:A.
20.解:连接AC、CF,如图,
∵四边形ABCD和四边形CEFG都是正方形,
∴∠ACD=45°,∠FCG=45°,AC=BC=,CF=CE=3,
∴∠ACF=45°+45°=90°,
在Rt△ACF中,AF==2,
∵H是AF的中点,
∴CH=AF=.
故选:A.
21.解:如图,作CF⊥L2,垂足为F,AE⊥L2,垂足为E,
∴由同角的余角相等得,∠FCD=∠EDA,
又∵AD=CD,∠AED=∠CFD=90°,
∴△AED≌△DFC,
∴ED=CF=4,AE=2,
∴AD=.
故选:C.
22.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
23.解:如图,连接AO,
∵四边形ABCD是正方形,
∴AB=AD=,BD=AB=2,∠DAB=90°,
又∵OM⊥AD,ON⊥AB,
∴四边形AMON是矩形,
∴AO=MN,
∵当AO⊥BD时,AO有最小值,
∴当AO⊥BD时,MN有最小值,
此时AB=AD,∠BAD=90°,AO⊥BD,
∴AO=BD=1,
∴MN的最小值为1,
故答案为:1.
24.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
25.(1)证明:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,
∴∠BAE+∠BAC=∠CAG+∠BAC,
即∠CAE=∠BAG,
∵在△ABG和△AEC中,
,
∴△ABG≌△AEC(SAS),
∴BG=CE;
(2)证明:设BG、CE相交于点N,
∵△ABG≌△AEC,
∴∠ACE=∠AGB,
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°,
∴∠CNG=360°﹣(∠NCF+∠NGF+∠F)=360°﹣(180°+90°)=90°,
∴BG⊥CE;
(3)解:过A作BG,CE的垂线段交于点P,Q,
∵△ABG≌△AEC,
∴AP=AQ,
∴AM是角平分线,
∴∠AMC=45°,
∴∠AME=135°.
26.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
27.解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°.
∴∠DAP+∠BAP=90°.
又∠EAP+∠BAP=90°,
∴∠EAP=∠DAP.
又AE=AP,
∴△APD≌△AEB(SAS).
所以①正确;
∵AE=AP,∠EAP=90°,
∴∠APE=∠AEP=45°,
∴∠APD=180°﹣45°=135°.
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠BEP=135°﹣45°=90°,
即EB⊥ED,②正确;
在等腰Rt△AEP中,利用勾股定理可得EP==2,
在Rt△BEP中,利用勾股定理可得BE==2,
∵B点到直线AE的距离小于BE,所以点B到直线AE的距离为2是错误的,
所以③错误;
在△AEB中,∠AEB=135°,AE=2,BE=2,
如图所示,过点A作AH⊥BE交BE延长线于H点.
在等腰Rt△AHE中,可得AH=HE=AE=.
所以BH=+2.
在Rt△AHB中利用勾股定理可得AB2=BH2+AH2,
即AB2=(+2)2+()2=32+4,
所以S正方形ABCD=32+4.
所以④正确.
所以只有①和②、④的结论正确.
故选:C.
28.解:(1)EF2=AF2+BF2.
理由:如图1,∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠EOF=∠AOB=90°,
∴∠EOA=∠FOB,
在△EOA和△FOB中,
,
∴△EOA≌△FOB(ASA),
∴AE=BF,
在Rt△EAF中,EF2=AE2+AF2=AF2+BF2;
(2)在BC上取一点H,使得BH=AE.
∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBH,∠AOB=90°,
在△OAE和△OBH中,
∴△OAE≌△OBH(SAS),
∴AE=BH,∠AOE=∠BOH,OE=OH,
∵∠EOF=45°,
∴∠AOE+∠BOF=45°,
∴∠BOF+∠BOH=45°,
∴∠FOE=∠FOH=45°,
在△FOE和△FOH中 ,
,
∴△FOE≌△FOH(SAS),
∴EF=FH,
∵∠FBH=90°,
∴FH2=BF2+BH2,
∴EF2=BF2+AE2,
29.解:(1)如图,取AD的中点F,连接FM.
∵∠FDM+∠DMA=∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∵AF=AD=AB=AM=MB=DF,
∵BN平分∠CBE,即∠NBE=∠CBE=45°,
又∵AM=AF,
∴∠AFM=45°,
∴∠DFM=∠MBN=135°.
∵DF=MB,
在△DFM和△MBN中
,
∴△DFM≌△MBN(ASA).
∴DM=MN.
(2)结论“DM=MN”仍成立.
证明如下:如图,在AD上截取AF'=AM,连接F'M.
∵DF'=AD﹣AF',MB=AB﹣AM,AD=AB,AF'=AM,
∴DF'=MB.
∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN.
又∠DF'M=∠MBN=135°,
在△DF'M和△MBN中
,
∴△DF'M≌△MBN(ASA).
∴DM=MN.
30.证明:(1)由题意画出图形,如下图,
∵四边形ABDE是正方形,
∴AB=AE,∠BAE=90°.
∵四边形ACFG是正方形,
∴AG=AC,∠GAC=90°.
∵∠BAG=∠BAE=∠EAG=90°+∠EAG,
∠EAC=∠GAC+∠EAG=90°+∠EAG,
∴∠BAG=∠EAG.
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS).
∴BG=CE.
解:(2)∵△BAG≌△EAC,
∴∠BGA=∠ECA.
设EC与AG交于点N,
∵∠MNG=∠ANC,
∴∠GMN=∠CAN.
∵四边形ACFG是正方形,
∴∠GAC=90°,
∴∠GMC=90°.
∴∠BMC=90°.
连接GC,如图,
∵四边形ACFG是正方形,
∴∠AGC=45°.
∵∠GMC=∠GAC=90°,
∴A,M,G.C四点共圆.
∴∠AMC=∠AGC=45°.
解:(3)∵△BAG≌△EAC,
∴BG=EC=a,S△BAG=S△EAC.
∵,
,
∴S△ABM=S△BAG,S△ACM=S△EAC.
∴=.
31.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
十.正方形的判定与性质
32.解:如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故选:D.
一.直角三角形斜边上的中线
1.直角三角形斜边上的高与中线分别是5和6,则它的面积是( )
A.60 B.50 C.40 D.30
二.矩形的判定
2.若O是四边形ABCD对角线的交点且OA=OB=OC=OD,则四边形ABCD是( )
A.平行四边形 B.矩形 C.正方形 D.菱形
3.如图,已知平行四边形ABCD的对角线AC,BD相交于点O,下列选项能使平行四边形ABCD成为矩形的条件是( )
A.AB=AD B.∠AOB=60° C.AC⊥BD D.∠OBC=∠OCB
三.矩形的性质
4.已知矩形的对角线为1,面积为m,则矩形的周长为( )
A. B. C.2 D.2
5.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10 B.8 C.6 D.4
6.如图,在矩形ABCD中,AB=9,AD=12,对角线AC,BD相交于点O,过点O作OE⊥AC交AD于点E,则ED的长为( )
A. B. C.2 D.
7.如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠EAB,则∠EAC的度数为 .
8.如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当时间t为( )s时,能够使△BPE与△CQP全等.
A.1 B.1或4 C.1或2 D.2或4
四.矩形的判定与性质
9.如图:在△ABC中,CE、CF分别平分∠ACB与它的邻补角∠ACD,AE⊥CE于E,AF⊥CF于F,直线EF分别交AB、AC于M、N.
(1)求证:四边形AECF为矩形;
(2)试猜想MN与BC的关系,并证明你的猜想;
(3)如果四边形AECF是菱形,试判断△ABC的形状,直接写出结果,不用说明理由.
五.菱形的判定
10.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定平行四边形ABCD为菱形的是( )
A.∠AOB=∠BOC B.∠ABO=∠OBC C.AB=BC D.AC=BD
六.菱形的性质
11.如图,在菱形ABCD中,AE,AF分别垂直平分BC,CD,垂足分别为E,F,则∠EAF的度数是( )
A.30° B.45° C.60° D.90°
12.如图,已知点A的坐标是,2),点B的坐标是(﹣1,,菱形ABCD的对角线交于坐标原点O,则点D的坐标是 .
13.已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求∠BCD的度数.
七.菱形的判定与性质
14.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,以A为圆心,AB长为半径画弧交AD于F,若BF=12,AB=10,则AE的长为( )
A.16 B.15 C.14 D.13
15.如图, ABCD的对角线AC、BD相交于点O.AB=10,AC=12,BD=16.
(1)求证: ABCD是菱形;
(2)若点P是对角线BD上一动点(不与点B、D重合),PE⊥AB于点E,PF⊥AD于点F,PE+PF是否为定值?若是,求出这个定值;若不是,请说明理由.
八.正方形的判定
16.如图,两张对边平行且等宽的纸条交叉叠放在一起,重合部分构成的四边形ABCD是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
17.两条对角线相等且互相垂直平分的四边形是( )
A.平行四边形 B.矩形 C.菱形 D.正方形
18.如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF.
(1)求证:△EBF≌△ABC;
(2)求证:四边形AEFD是平行四边形;
(3)△ABC满足 时,四边形AEFD是正方形.
九.正方形的性质
19.如图,在正方形ABCD的外侧,作等边三角形CDE,连接AE.则∠DAE的度数是( )
A.15° B.20° C.12.5° D.10°
20.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A. B. C. D.2
21.如图,直线L1、L2、L3分别过正方形ABCD的三个顶点A、D、C,且相互平行,若L1、L2的距离为2,L2、L3的距离为4,则正方形的边长是( )
A. B. C. D.
22.如图所示,在正方形ABCD中,以AB为边向正方形外作等边三角形ABE,连接CE、BD交于点G,连接AG,那么∠AGD的度数是 度.
23.如图,正方形ABCD的边长为,O是对角线BD上一动点(点O与端点B,D不重合),OM⊥AD于点M,ON⊥AB于点N,连接MN,则MN长的最小值为 .
24.如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上且A(﹣3,0),B(2,b),则正方形ABCD的面积是( )
A.20 B.16 C.34 D.25
25.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.
(1)求证:BG=CE;
(2)求证:CE⊥BG;
(3)求:∠AME的度数.
26.如图,点P在正方形ABCD的对角线AC上,点E在边BC上,且PE=PB.
(1)求证:PE=PD;
(2)试探究BC2,EC2,PE2三者之间满足的等量关系,并证明你的结论.
27.如图,点E是正方形ABCD外一点,连接AE、BE和DE,过点A作AE垂线交DE于点P.若AE=AP=2,PB=6.下列结论:①△APD≌△AEB;②EB⊥ED;③点B到直线AE的距离为2;④S正方形ABCD=32+4.则正确结论的个数是( )
A.1 B.2 C.3 D.4
28.如图,已知四边形ABCD是正方形,对角线AC、BD相交于O.
(1)如图1,设E、F分别是AD、AB上的点,且∠EOF=90°,线段AF、BF和EF之间存在一定的数量关系.请你用等式直接写出这个数量关系;
(2)如图2,设E、F分别是AB上不同的两个点,且∠EOF=45°,请你用等式表示线段AE、BF和EF之间的数量关系,并证明.
29.如图①,正方形ABCD中,M是AB的中点,E是延长线上一点.MN⊥DM,且交∠CBE的平分线于N.
(1)若点F是AD的中点,求证:MD=MN;
(2)若将上述条件中的“M是AB的中点”改为“M是AB上的任意一点”,其它条件不变.如图②所示,则结论“MD=MN”是否成立.若成立,给出证明;若不成立,请说明理由.
30.如图,已知在△ABC中,∠A是钝角,以AB为边作正方形ABDE,使△ABC正方形ABDE分居在AB两侧,以AC为边作正方形ACFG,使△ABC正方形ACFG分居在AC两侧,BG与CE交于点M,连接AM.
(1)求证:BG=CE;
(2)求:∠AMC的度数;
(3)若BG=a,MG=b,ME=c,求:S△ABM:S△ACM(结果可用含有a,b,c的式子表示).
31.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
十.正方形的判定与性质
32.如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:①OA=OD;②AD⊥EF;③当∠A=90°时,四边形AEDF是正方形;④AE+DF=AF+DE.其中正确的是( )
A.②③ B.②④ C.①③④ D.②③
参考答案
一.直角三角形斜边上的中线
1.解:∵直角三角形斜边上的中线CD是6,
∴斜边AB长为:2×CD=6×2=12,
∴它的面积=×AB×CE=×12×5=30,
故选:D.
二.矩形的判定
2.解:∵OA=OB=OC=OD,
∴四边形ABCD是平行四边形,AC=BD,
∴平行四边形ABCD是矩形.
故选:B.
3.解:A、∵四边形ABCD是平行四边形,AB=AD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、由四边形ABCD是平行四边形,∠AOB=60°,不能判定平行四边形ABCD为矩形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,AC⊥BD,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵∠OBC=∠OCB,
∴OB=OC,
∴AC=BD,
∴平行四边形ABCD是矩形,故选项D符合题意;
故选:D.
三.矩形的性质
4.解:设矩形的长、宽分别为a、b,
∵矩形的对角线为1,面积为m,
∴a +b =1,ab=m,
∴a+b===,
∴矩形的周长为2(a+b)=2,
故选:C.
5.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠ADE,
又∵∠DEC=∠AED,
∴∠ADE=∠AED,
∴AE=AD=10,
在直角△ABE中,BE==8.
故选:B.
6.解:连接EC,如图,
∵四边形ABCD是矩形,
∴AO=OC.
∵EO⊥AC,
∴OE为线段AC的垂直平分线.
∴EC=AE.
设DE=x,则AE=12﹣x.
∴EC=12﹣x,
在Rt△ECD中,
∵EC2=DE2+DC2,
∴(12﹣x)2=x2+92.
解得:x=.
∴DE=.
故选:A.
7.解:∵四边形ABCD是矩形,AC、BD是矩形的对角线且相交于O,
∴OA=OB,
∴∠BAC=∠ABD,
∵∠DAE=3∠BAE,∠DAE+∠BAE=90°,
∴∠BAE=22.5°,∠DAE=67.5°.
∵在矩形ABCD,∠DAE+∠ADB=90°,∠ADB+∠ABD=90°,
∴∠ABD=∠DAE=67.5°,即∠BAC=∠ABD=67.5°,
∴∠EAC=∠BAC﹣∠BAE=67.5°﹣22.5°=45°,
故答案为:45°.
8.解:分两种情况:
①当EB=PC,BP=QC时,△BPE≌△CQP,
∵AB=20cm,AE=6cm,
∴EB=14cm,
∴PC=14cm,
∵BC=16cm,
∴BP=2cm,
∵点P从点B出发在线段BC上以2cm/s的速度向点C运动,
∴t=2÷2=1(s);
②当BP=CP,BE=QC时,△BEP≌△CQP,
由题意得:2t=16﹣2t,
解得:t=4(s),
故选:B.
四.矩形的判定与性质
9.(1)证明:∵AE⊥CE于E,AF⊥CF于F,
∴∠AEC=∠AFC=90°,
又∵CE、CF分别平分∠ACB与它的邻补角∠ACD,
∴∠BCE=∠ACE,∠ACF=∠DCF,
∴∠ACE+∠ACF=(∠BCE+∠ACE+∠ACF+∠DCF)=×180°=90°,
∴三个角为直角的四边形AECF为矩形.
(2)结论:MN∥BC且MN=BC.
证明:∵四边形AECF为矩形,
∴对角线相等且互相平分,
∴NE=NC,
∴∠NEC=∠ACE=∠BCE,
∴MN∥BC,
又∵AN=CN(矩形的对角线相等且互相平分),
∴N是AC的中点,
若M不是AB的中点,则可在AB取中点M1,连接M1N,
则M1N是△ABC的中位线,MN∥BC,
而MN∥BC,M1即为点M,
所以MN是△ABC的中位线(也可以用平行线等分线段定理,证明AM=BM)
∴MN=BC;
法二:延长MN至K,使NK=MN,
因为对角线互相平分,
所以AMCK是平行四边形,KC∥MA,KC=AM因为MN∥BC,
所以MBCK是平行四边形,MK=BC,
所以MN=BC
(3)解:△ABC是直角三角形(∠ACB=90°).
理由:∵四边形AECF是菱形,
∴AC⊥EF,
∵EF∥AC,
∴AC⊥CB,
∴∠ACB=90°.即△ABC是直角三角形.
五.菱形的判定
10.解:A、∵∠AOB=∠BOC,∠AOB+∠BOC=180°,
∴∠AOB=∠BOC=90°,
∴AC⊥BD,
∴平行四边形ABCD是菱形,故选项A不符合题意;
B、过O作OE⊥AB于E,OF⊥BC于F,如图所示:
∵∠ABO=∠OBC,
∴OE=OF,
∵四边形ABCD是平行四边形,
∴OA=OC,
∴△AOB的面积=△COB的面积,
又∵△AOB的面积=AB×OE,△COB的面积=BC×OF,
∴AB×OE=BC×OF,
∴AB=BC,
∴平行四边形ABCD是菱形,故选项B不符合题意;
C、∵平行四边形ABCD中,AB=BC,
∴平行四边形ABCD是菱形,故选项C不符合题意;
D、∵平行四边形ABCD中,AC=BD,
∴平行四边形ABCD是矩形,故选项D符合题意;
故选:D.
六.菱形的性质
11.解:连接AC,如图:
∵AE,AF分别垂直平分BC,CD,
∴AB=AC,AD=AC,∠AEC=∠AFC=90°,
又∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∴AB=AC=BC=AD=CD,
∴△ABC、△ACD是等边三角形,
∴∠B=∠ACB=∠ACD=60°,
∴∠BCD=120°,
∴在四边形AECF中,∠EAF=360°﹣90°﹣90°﹣120°=60°.
故选:C.
12.解:∵四边形ABCD为菱形,
∴OB=OD,
又∵点O为坐标原点,
∴点B和点D关于原点对称,
∵点B的坐标为(﹣1,﹣),
∴D点坐标为(1,),
故答案为:(1,).
13.解:(1)∵四边形ABCD是菱形,
∴AB∥CD,
∴∠1=∠ACD,
∵∠1=∠2,
∴∠ACD=∠2,
∴CM=DM,
∵ME⊥CD,
∴CE=DE=CD=1,
∴BC=CD=2;
(2)连接BD,
∵四边形ABCD是菱形,
∴CB=CD,∠ACB=∠ACD,
∵F为边BC的中点,
∴CF=CB,
∵CE=CD,
∴CE=CF,
在△MCF和△NCE中
∴△FCM≌△ECM(SAS),
∴∠CFM=∠CEM=90°,
∴DF⊥BC,
∴BD=CD,
∴BC=CD=BC,
∴△BCD是等边三角形,
∴∠BCD=60°.
七.菱形的判定与性质
14.解:连接EF,AE与BF交于点O,如图,
∵AO平分∠BAD,
∴∠1=∠2,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
同理:AF=BE,
又∵AF∥BE,
∴四边形ABEF是平行四边形,
∴四边形ABEF是菱形,
∴AE⊥BF,OB=OF=6,OA=OE,
在Rt△AOB中,由勾股定理得:OA===8,
∴AE=2OA=16.
故选:A.
15.(1)证明:∵四边形ABCD是平行四边形,AC=12,BD=16,AB=10,
∴AO=CO=AC=6,BO=DO=BD=8,
∵62+82=102,
∴AO2+BO2=AB2,
∴∠AOB=90°,
∴AC⊥BD,
∴ ABCD是菱形;
(2)解:是定值,
连接AP,过B作BH⊥DA于H,
∵四边形ABCD是菱形,
∴AB=AD=10,S△ABD=S菱形ABCD=×AC BD=×12×16=48,
∵S△ABD=S△ABO+S△ADO=AB PE+AD PF=AD(PE+PF)=AD BH,
∴PE+PF=BH,
∵S△ABD=AD BH=×10 BH=48,
∴BH=,
∴PE+PF=.
故PE+PF定值为.
八.正方形的判定
16.解:由图可知,过A点作AE⊥BC于E,AF⊥CD于F,
∵两条纸条宽度相等,
∴AE=AF.
∵AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
∵SABCD=BC×AE=CD AF.
又∵AE=AF,
∴BC=CD,
∴四边形ABCD为菱形.
故选:B.
17.解:根据正方形的判别方法知,两条对角线互相垂直平分的四边形是菱形,且相等又可判定为正方形,故选D.
18.(1)证明:∵△ABE、△BCF为等边三角形,
∴AB=BE=AE,BC=CF=FB,∠ABE=∠CBF=60°,
∴∠ABE﹣∠ABF=∠FBC﹣∠ABF,
即∠CBA=∠FBE,
在△EBF和△ABC中,
,
∴△EBF≌△ABC(SAS);
(2)证明:∵△EBF≌△ABC,
∴EF=AC,
又∵△ADC为等边三角形,
∴CD=AD=AC,
∴EF=AD=DC,
同理可得△ABC≌△DFC,
∴AB=AE=DF,
∴四边形AEFD是平行四边形;
(3)解:当AB=AC,∠BAC=150°时,四边形ADEF是正方形.
理由是:∵△ABE、△ACD为等边三角形,
∴AB=AE,AC=AD,∠EAB=∠DAC=60°,
∵AB=AC,
∴AE=AD,
∵四边形ADEF是平行四边形,
∴四边形ADEF是菱形,
∵∠BAC=150°,
∴∠EAD=360°﹣60°﹣60°﹣150°=90°,
∴平行四边形ADEF是正方形,
故答案为:AB=AC,∠BAC=150°.
九.正方形的性质
19.解:∵四边形ABCD是正方形,
∴∠ADC=90°,AD=DC,
∵△CDE是等边三角形,
∴DE=DC,∠EDC=60°,
∴∠ADE=90°+60°=150°,AD=ED,
∴∠DAE=∠DEA=(180°﹣∠ADE)=15°,
故选:A.
20.解:连接AC、CF,如图,
∵四边形ABCD和四边形CEFG都是正方形,
∴∠ACD=45°,∠FCG=45°,AC=BC=,CF=CE=3,
∴∠ACF=45°+45°=90°,
在Rt△ACF中,AF==2,
∵H是AF的中点,
∴CH=AF=.
故选:A.
21.解:如图,作CF⊥L2,垂足为F,AE⊥L2,垂足为E,
∴由同角的余角相等得,∠FCD=∠EDA,
又∵AD=CD,∠AED=∠CFD=90°,
∴△AED≌△DFC,
∴ED=CF=4,AE=2,
∴AD=.
故选:C.
22.解:∵四边形ABCD是正方形,
∴AB=BC=AD=CD,∠ABC=90°,∠ADG=∠CDG,∠ABD=45°,
∵GD=GD,
∴△ADG≌△CDG,
∴∠AGD=∠CGD,
∵∠CGD=∠EGB,
∴∠AGD=∠EGB,
∵△ABE是等边三角形,
∴AB=BE,∠ABE=60°,
∴BE=BC,∠EBC=150°,
∴∠BEC=∠ECB=15°,
∴∠BGE=180°﹣∠BEC﹣∠EBG=180°﹣15°﹣60°﹣45°=60°,
∴∠AGD=60°
故答案为60.
23.解:如图,连接AO,
∵四边形ABCD是正方形,
∴AB=AD=,BD=AB=2,∠DAB=90°,
又∵OM⊥AD,ON⊥AB,
∴四边形AMON是矩形,
∴AO=MN,
∵当AO⊥BD时,AO有最小值,
∴当AO⊥BD时,MN有最小值,
此时AB=AD,∠BAD=90°,AO⊥BD,
∴AO=BD=1,
∴MN的最小值为1,
故答案为:1.
24.解:作BM⊥x轴于M.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴在△DAO和△ABM中,
∴△DAO≌△ABM(AAS),
∴OA=BM,AM=OD,
∵A(﹣3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD==,
∴正方形ABCD的面积=34,
故选:C.
25.(1)证明:在正方形ABDE和ACFG中,AB=AE,AC=AG,∠BAE=∠CAG=90°,
∴∠BAE+∠BAC=∠CAG+∠BAC,
即∠CAE=∠BAG,
∵在△ABG和△AEC中,
,
∴△ABG≌△AEC(SAS),
∴BG=CE;
(2)证明:设BG、CE相交于点N,
∵△ABG≌△AEC,
∴∠ACE=∠AGB,
∵∠NCF+∠NGF=∠ACF+∠AGF=90°+90°=180°,
∴∠CNG=360°﹣(∠NCF+∠NGF+∠F)=360°﹣(180°+90°)=90°,
∴BG⊥CE;
(3)解:过A作BG,CE的垂线段交于点P,Q,
∵△ABG≌△AEC,
∴AP=AQ,
∴AM是角平分线,
∴∠AMC=45°,
∴∠AME=135°.
26.(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠ACB=∠ACD,
在△PBC和△PDC中,
,
∴△PBC≌△PDC(SAS),
∴PB=PD,
∵PE=PB,
∴PE=PD;
(2)解:BC2+EC2=2PE2,证明如下:
连接DE,如图所示:
∵四边形ABCD是正方形,
∴∠BCD=90°,BC=CD,
由(1)得:△PBC≌△PDC,
∴∠PBC=∠PDC,
∵PE=PB,
∴∠PBC=∠PEB,
∴∠PDC=∠PEB,
∵∠PEB+∠PEC=180°,
∴∠PDC+∠PEC=180°,
∴∠EPD=360°﹣(∠PDC+∠PEC)﹣∠BCD=360°﹣180°﹣90°=90°,
又∵PE=PD,
∴△PDE是等腰直角三角形,
∴DE2=PE2+PD2=2PE2,
在Rt△CDE中,由勾股定理得:CD2+EC2=DE2,
∴BC2+EC2=2PE2.
27.解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°.
∴∠DAP+∠BAP=90°.
又∠EAP+∠BAP=90°,
∴∠EAP=∠DAP.
又AE=AP,
∴△APD≌△AEB(SAS).
所以①正确;
∵AE=AP,∠EAP=90°,
∴∠APE=∠AEP=45°,
∴∠APD=180°﹣45°=135°.
∵△APD≌△AEB,
∴∠AEB=∠APD=135°,
∴∠BEP=135°﹣45°=90°,
即EB⊥ED,②正确;
在等腰Rt△AEP中,利用勾股定理可得EP==2,
在Rt△BEP中,利用勾股定理可得BE==2,
∵B点到直线AE的距离小于BE,所以点B到直线AE的距离为2是错误的,
所以③错误;
在△AEB中,∠AEB=135°,AE=2,BE=2,
如图所示,过点A作AH⊥BE交BE延长线于H点.
在等腰Rt△AHE中,可得AH=HE=AE=.
所以BH=+2.
在Rt△AHB中利用勾股定理可得AB2=BH2+AH2,
即AB2=(+2)2+()2=32+4,
所以S正方形ABCD=32+4.
所以④正确.
所以只有①和②、④的结论正确.
故选:C.
28.解:(1)EF2=AF2+BF2.
理由:如图1,∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBF=45°,AC⊥BD,
∴∠EOF=∠AOB=90°,
∴∠EOA=∠FOB,
在△EOA和△FOB中,
,
∴△EOA≌△FOB(ASA),
∴AE=BF,
在Rt△EAF中,EF2=AE2+AF2=AF2+BF2;
(2)在BC上取一点H,使得BH=AE.
∵四边形ABCD是正方形,
∴OA=OB,∠OAE=∠OBH,∠AOB=90°,
在△OAE和△OBH中,
∴△OAE≌△OBH(SAS),
∴AE=BH,∠AOE=∠BOH,OE=OH,
∵∠EOF=45°,
∴∠AOE+∠BOF=45°,
∴∠BOF+∠BOH=45°,
∴∠FOE=∠FOH=45°,
在△FOE和△FOH中 ,
,
∴△FOE≌△FOH(SAS),
∴EF=FH,
∵∠FBH=90°,
∴FH2=BF2+BH2,
∴EF2=BF2+AE2,
29.解:(1)如图,取AD的中点F,连接FM.
∵∠FDM+∠DMA=∠BMN+∠DMA=90°,
∴∠FDM=∠BMN,
∵AF=AD=AB=AM=MB=DF,
∵BN平分∠CBE,即∠NBE=∠CBE=45°,
又∵AM=AF,
∴∠AFM=45°,
∴∠DFM=∠MBN=135°.
∵DF=MB,
在△DFM和△MBN中
,
∴△DFM≌△MBN(ASA).
∴DM=MN.
(2)结论“DM=MN”仍成立.
证明如下:如图,在AD上截取AF'=AM,连接F'M.
∵DF'=AD﹣AF',MB=AB﹣AM,AD=AB,AF'=AM,
∴DF'=MB.
∵∠F'DM+∠DMA=∠BMN+∠DMA=90°,
∴∠F'DM=∠BMN.
又∠DF'M=∠MBN=135°,
在△DF'M和△MBN中
,
∴△DF'M≌△MBN(ASA).
∴DM=MN.
30.证明:(1)由题意画出图形,如下图,
∵四边形ABDE是正方形,
∴AB=AE,∠BAE=90°.
∵四边形ACFG是正方形,
∴AG=AC,∠GAC=90°.
∵∠BAG=∠BAE=∠EAG=90°+∠EAG,
∠EAC=∠GAC+∠EAG=90°+∠EAG,
∴∠BAG=∠EAG.
在△BAG和△EAC中,
,
∴△BAG≌△EAC(SAS).
∴BG=CE.
解:(2)∵△BAG≌△EAC,
∴∠BGA=∠ECA.
设EC与AG交于点N,
∵∠MNG=∠ANC,
∴∠GMN=∠CAN.
∵四边形ACFG是正方形,
∴∠GAC=90°,
∴∠GMC=90°.
∴∠BMC=90°.
连接GC,如图,
∵四边形ACFG是正方形,
∴∠AGC=45°.
∵∠GMC=∠GAC=90°,
∴A,M,G.C四点共圆.
∴∠AMC=∠AGC=45°.
解:(3)∵△BAG≌△EAC,
∴BG=EC=a,S△BAG=S△EAC.
∵,
,
∴S△ABM=S△BAG,S△ACM=S△EAC.
∴=.
31.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
十.正方形的判定与性质
32.解:如果OA=OD,则四边形AEDF是矩形,没有说∠A=90°,不符合题意,故①错误;
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,,
∴△AED≌△AFD(AAS),
∴AE=AF,DE=DF,
∴AE+DF=AF+DE,故④正确;
∵在△AEO和△AFO中,,
∴△AEO≌△AFO(SAS),
∴EO=FO,
又∵AE=AF,
∴AO是EF的中垂线,
∴AD⊥EF,故②正确;
∵当∠A=90°时,四边形AEDF的四个角都是直角,
∴四边形AEDF是矩形,
又∵DE=DF,
∴四边形AEDF是正方形,故③正确.
综上可得:正确的是:②③④,
故选:D.
