对数函数的图像和性质公开课
图片预览



文档简介
课件10张PPT。5.3 对数函数的图像和性质任中 魏我们把函数 叫作对数函数,其中值域是定义域是叫作对数函数的底数。1.对数函数的概念:2.指数函数 和对数函数
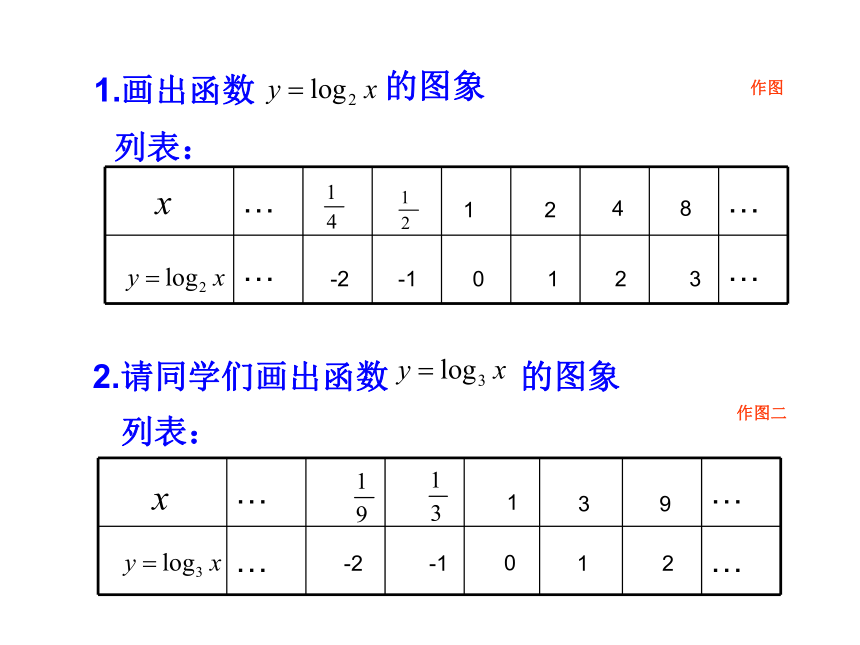
互为反函数。列表:3210-2-12.请同学们画出函数 的图象列表:-2-1012作图作图二图象特征
(1)图象在 轴的右侧;
当 时,图象在第四象限;
当 ,图象在第一象限;
(2)图象过点
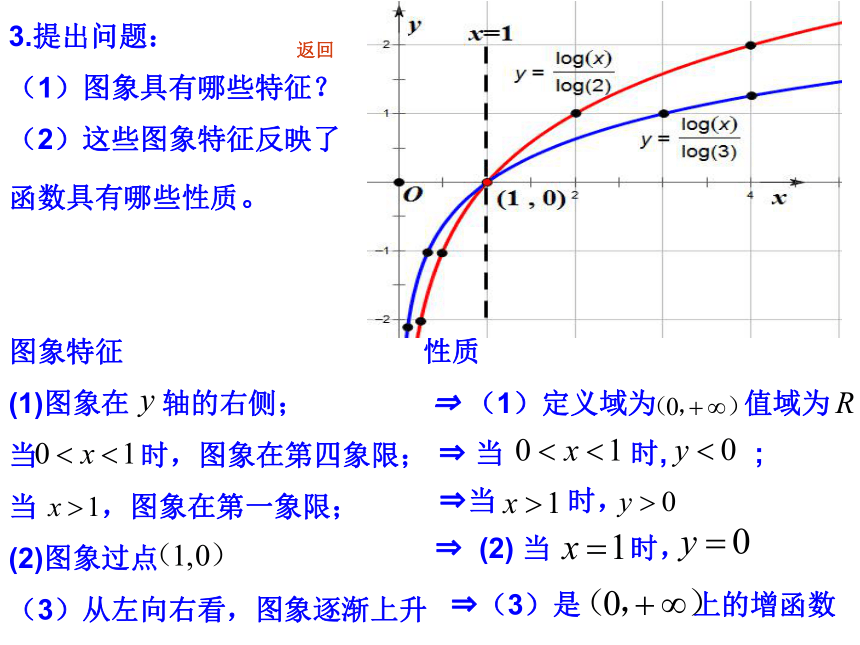
(3)从左向右看,图象逐渐上升3.提出问题:
(1)图象具有哪些特征?
(2)这些图象特征反映了函数具有哪些性质。 ?(3)是 上的增函数? (2) 当 时,性质
? (1)定义域为 值域为? 当 时, ;返回?当 时,(3)这两个函数的底数不同,图象有什么不同点?4.提出问题:
(1)当把底数换成4,5,6时,函数图象特征和 图象相同吗? (2)提出猜想:当底数 时,函数 具有哪些 特征和性质,并归纳。总结图象特征相同底数越大,在 时更靠近 轴,在 时更靠近 轴。图象概括:当底数 时,对数函数是 上的增函数,底数 越大,在 时更靠近 轴,在 时更靠近 轴。(4)总结归纳,当底数 时,底数的改变会对函数产生哪些影响?练习操作回回2练习1:试在同一坐标系画出 草图练习2:试在同一坐标系画出 草图下后练习5.在同一坐标系作出函数 图象,归纳总结出
当 时,函数 具有哪些特征和性质。6.提出问题:当底数 时,底数 的改变会对对数函数产生哪些影响?操作概括:当底数 时,对数函数是 上的减函数,底数 值越小,当 时,其图像越靠近 轴,
当 时,其图像越靠近 轴。总结解:5.例题:
例一.求下列函数的定义域:
(1) (2)例二.比较下列各题中两个数的大小
(1) (2)所以(1)因为 ,即所以定义域为(2)因为所以定义域为解:(1)函数 是增函数,因为所以因为(2)函数 是减函数6.观察在同一坐标系内函数 与函数 的图象,分析它们之间的关系。解:图象关于直线 对称
互为反函数。列表:3210-2-12.请同学们画出函数 的图象列表:-2-1012作图作图二图象特征
(1)图象在 轴的右侧;
当 时,图象在第四象限;
当 ,图象在第一象限;
(2)图象过点
(3)从左向右看,图象逐渐上升3.提出问题:
(1)图象具有哪些特征?
(2)这些图象特征反映了函数具有哪些性质。 ?(3)是 上的增函数? (2) 当 时,性质
? (1)定义域为 值域为? 当 时, ;返回?当 时,(3)这两个函数的底数不同,图象有什么不同点?4.提出问题:
(1)当把底数换成4,5,6时,函数图象特征和 图象相同吗? (2)提出猜想:当底数 时,函数 具有哪些 特征和性质,并归纳。总结图象特征相同底数越大,在 时更靠近 轴,在 时更靠近 轴。图象概括:当底数 时,对数函数是 上的增函数,底数 越大,在 时更靠近 轴,在 时更靠近 轴。(4)总结归纳,当底数 时,底数的改变会对函数产生哪些影响?练习操作回回2练习1:试在同一坐标系画出 草图练习2:试在同一坐标系画出 草图下后练习5.在同一坐标系作出函数 图象,归纳总结出
当 时,函数 具有哪些特征和性质。6.提出问题:当底数 时,底数 的改变会对对数函数产生哪些影响?操作概括:当底数 时,对数函数是 上的减函数,底数 值越小,当 时,其图像越靠近 轴,
当 时,其图像越靠近 轴。总结解:5.例题:
例一.求下列函数的定义域:
(1) (2)例二.比较下列各题中两个数的大小
(1) (2)所以(1)因为 ,即所以定义域为(2)因为所以定义域为解:(1)函数 是增函数,因为所以因为(2)函数 是减函数6.观察在同一坐标系内函数 与函数 的图象,分析它们之间的关系。解:图象关于直线 对称
