第二章 气体、固体和液体 全章复习(共15张ppt)
文档属性
| 名称 | 第二章 气体、固体和液体 全章复习(共15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 689.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第二章《气体、固体和液体》
全章复习
(1)体积V:容器的容积;
(2)压强p:微观解释、计算方式;
(3)温度T:热平衡、温标。
(1)玻意耳定律:表述、公式、p-V图及p- 图;
(2)盖-吕萨克定律:表述、公式、V-T图及V-t图;
(3)查理定律:表述、公式、p-T图及p-t图。
(1)单晶体:举例、特性,微观结构;
(2)多晶体:举例、特性,微观结构;
(3)非晶体:举例、特性。
气体、固体与液体
1.气体的状态参量
2.气体实验定律
3.固体
4.液体
(1)液体的表面张力:成因、方向、效果;
(2)浸润和不浸润:现象、成因;
(3)毛细现象:现象、成因、应用;
(4)液晶“三态”。
一、知识结构
1.体积 V:容器的容积。要用几何关系确定。
单位m3,L、mL等, 1L=103mL =10-3m3
2.压强 p:由大量气体分子对器壁的碰撞引起。
单位Pa(帕),1atm=1.01×105Pa=76cmHg
影响因素:温度(气体分子热运动的平均动能)、体积(分子数密度);
计算方法:根据动力学方程确定、根据连能管原理确定等。
3.热力学温度T :分子热运动平均动能的标志。
单位K(开) ,热学基本单位, T = t + 273 K,ΔT= Δt
测温原理:热平衡定律—若两个系统分别与第三个系统达到热平衡,那么这两个系统彼此之间也必定处于热平衡。
处于热平衡的两个系统必定具有相同的温度。
p2=40atm
V2=48mL
t2=941K(668oC)
气体溢出时,想象它的体积”增大”
二、应用与体会:描述气体状态的参量
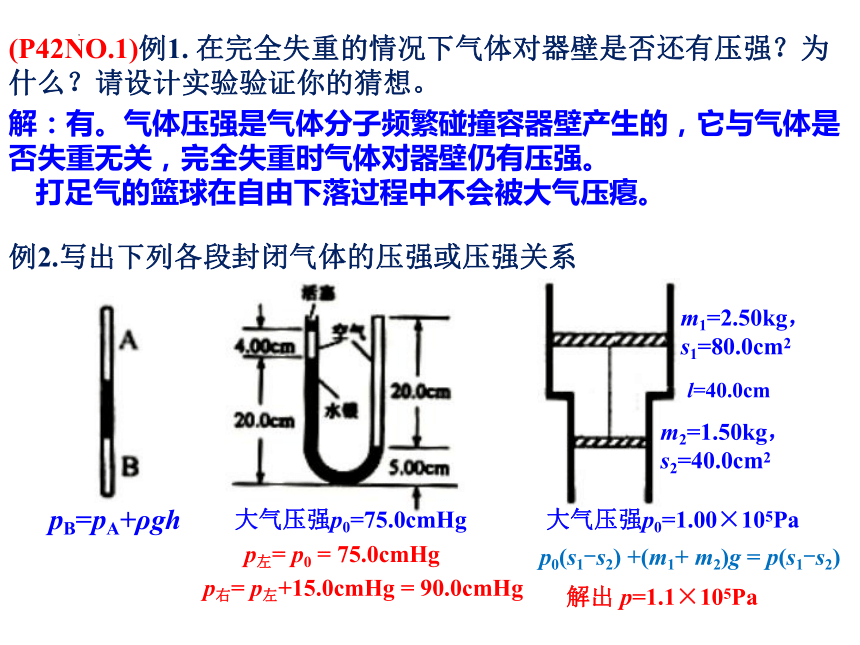
例2.写出下列各段封闭气体的压强或压强关系
大气压强p0=75.0cmHg
pB=pA+ρgh
(P42NO.1)例1. 在完全失重的情况下气体对器壁是否还有压强?为什么?请设计实验验证你的猜想。
大气压强p0=1.00×105Pa
m1=2.50kg,
s1=80.0cm2
m2=1.50kg,
s2=40.0cm2
l=40.0cm
解:有。气体压强是气体分子频繁碰撞容器壁产生的,它与气体是否失重无关,完全失重时气体对器壁仍有压强。
打足气的篮球在自由下落过程中不会被大气压瘪。
p左= p0 = 75.0cmHg
p右= p左+15.0cmHg = 90.0cmHg
p0(s1-s2) +(m1+ m2)g = p(s1-s2)
解出 p=1.1×105Pa
(P43NO.2)例3.超市中有一种“强力吸盘挂钩”如图所示。下图是它的工作原理示意图。使用时, 按住锁扣把吸盘紧压在墙上(图甲),吸盘中的空气被挤出一部分。然后要把锁扣扳下(图乙),让锁扣以盘盖为依托把吸盘向外拉出。在拉起吸盘的同时,锁扣对盘盖施加压力, 致使盘盖以很大的压力压住吸盘。为什么锁扣 扳下后,盘盖对吸盘会产生很大的压力?
解:扳下锁扣,外拉吸盘,其中气体体积变大、压强减小。
松手后吸盘内压强小于大气压,大气压使盘盖紧压到吸盘边缘,防止空气渗入。
1.气体实验定律
(1)玻意耳定律:某种气体的质量和温度一定时,p1V1=p2V2;
(2)查理定律:某种气体的质量和体积一定时, ;
(3)盖-吕萨克定律:某种气体的质量和压强一定时, 。
2.图像:等温线、等容线、等压线在不同图像上形态不同。
3.微观解释要点:
(1)温度是分子平均动能的标志;
(2)压强由分子热运动平均动能(T)、分子数密度(m、V) 决定。
二、应用与体会:气体实验定律及解释
(P29倒二段)例1. 试用分子动理论定性解释盖-吕萨克定律。
解:一定质量的某种理想气体,温度升高时,分子的平均动能增大;只有气体的体积同时增大,使分子的数密度减小,才能保持压强不变。这就是盖-吕萨克定律的微观解释。
(P25NO.1)例2. 在做“探究气体等温变化的规律”的实 验中,实验小组记录了一系列数据。但是,仅就以下表中的两组数据来看,小王和小李却有完全不同的看法:小王认为,这两组数据很好 地体现了 p 跟 V 成反比的规律,因为两组数据 p 和 V 的乘积几乎相等;小李却认为,如果把这两组数据在纵坐标轴为 p、横坐标轴为 的坐标系中描点,这两点连线的延长线将不经过坐标原点,因此这两组数据没有反映 p 跟 V 成 反比的规律。对此你有什么看法?
解:小李的说法正确。
因为数据变化量太小,即使实验误差很大,pV 乘积也不会有大的变化,看起来相等 。
应该比较Δp与ΔV 的数据,而作p- 图时,两点连线的斜率描述的就是变化量的关系。若图线不过原点则没有体现 p 跟 V 成反比的规律。
(P42NO.6)例3. 在一次科学晚会上,胡老师表演了一 个“马德堡半球实验”。他先取出两个在碗底各 焊接了铁钩的不锈钢碗,在一个碗里烧了一些纸,然后迅速把另一个碗扣上,再在碗的外面 浇水,使其冷却到环境温度。用两段绳子分别 钩着铁钩朝相反的方向拉,试图把两个碗拉开 。当两边的人各增加到 5 人时,才把碗拉开。已知碗口的直径为 20 cm,环境温度 为 15 ℃,实验过程中碗不变形,也不漏气,设 每人平均用力为 200 N。请你估算一下,两个不锈钢碗刚被扣上时,里面空气的温度是多少?
p
5F
p0
解:对一个碗受力平衡时,
p0S = pS + 5F
碗口圆面积 S=π
碗内气体等容变化,
p1=p0=1.00×105Pa,T1 = t +273K;
p2=p,T2 = (15 +273)K。
由查理定律,
代入数据解出 t =150.5 ℃
例4.如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0。开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K。现缓慢加热汽缸内气体,直至399.3 K。求:
(1)活塞刚离开B处时的温度TB;
(2)缸内气体最后的压强p;
(3)在图中画出整个过程的p-V图线。
p1=0.9p0
T0=297K
p2=p0
TB=
p3=p0
TA=
解:(1)等容过程,由查理定律有
解得TB=330K
(2)活塞刚到A温度TA,等压过程,由盖—吕萨克定律有
p=
T=399.3K
,解得TA=363K
因TA<399.3K,故气体还要做等容变化。
,解得p =1.1p0
(3)如图。
小结:用气体定律分析问题的一般步骤
(1)确定研究对象;
等质量的气体或活塞、液柱等封闭物。
(2)写出或表达气体的状态参量;
写数值或表达式,协调压强单位;分析几何关系和受力时要仔细。
(3)根据状态变化过程的特点,列出方程式;
准确建模:用哪个或联用多个气体定律列式。
(4) 求解未知量,审核结果。
联立方程:定律的、几何的、力学的等等。
分类 晶体
非晶体
单晶体 多晶体
实例 石英、云母、食盐 金属、蔗糖 玻璃、松香、橡胶
外形 规则 不规则
熔点 确定 不确定
物理性质 各向异性 各向同性
微观结构 原子规则排列 晶粒杂乱无章排列 原子不规则排列
联系 1.多晶体由单晶体组成; 2.同一原子可构成不同结构的晶体,如石墨和金刚石; 3.晶体和非晶体可相互转化,如石英晶体和石英玻璃。
二、应用与体会:固体的分类及特性比较
(P35NO.1)例1. 某人为了检验一块薄片物质是否为晶体, 做了一个实验。他以薄片的正中央O为坐标原 点,建立Oxy平面直角坐标系,在两个坐标轴 上分别取两点x1和y1,使x1和y1到O点的距离相等。在x1和y1上分别固定一个测温元件,再把一个针状热源放在O点,发现x1点和y1点的温度在缓慢升高,但两点温度的高低没有差异。 于是得出结论:这块薄片是非晶体。
请说明:以上结论科学吗?为什么?
解:不科学。该薄片不一定是晶体,也可能是多晶体。此外,两个特定方向的同性,并不能说明各个方向都同性。
位置 分子力特性 宏观表现
表面层 液体与气体接触的液体薄层 引力 表面张力。使液体表面收缩至最小。
附着层 液体与固体接触的液体薄层 引力或斥力 表面收缩时为不浸润;表面扩展时为浸润。
浸润液体在细管中上升、不浸润液体在细管中下降,称毛细现象。
(P41NO.4)例2.要想把凝固在衣料上的蜡迹去掉,可以把两层棉纸分别放在蜡迹处衣服的上面和下面,然后用热熨斗在棉纸上来回烫熨。为什么这样做可以去掉衣料上的蜡迹?
答:棉纸内有很多细小的孔道起着毛细管的作用,当蜡受热熔化成液体后,由于毛细现象,它们会被棉纸吸走。
二、应用与体会:液体的表面张力和毛细现象
总 结
1.气体实验定律的表述、公式、图像及微观解释
(1)正确理解(三个前提条件)、准确记忆(名称不乱、图形精准等);
(2)盖-吕萨克定律的微观解释(逻辑关系及措辞)。
2.主要问题类型
(1)压强的计算;
(2)实验定律的选用;
(3)气体状态的图像分析及转换;
(4)固体和液体的相关概念辨析。
第二章《气体、固体和液体》
全章复习
(1)体积V:容器的容积;
(2)压强p:微观解释、计算方式;
(3)温度T:热平衡、温标。
(1)玻意耳定律:表述、公式、p-V图及p- 图;
(2)盖-吕萨克定律:表述、公式、V-T图及V-t图;
(3)查理定律:表述、公式、p-T图及p-t图。
(1)单晶体:举例、特性,微观结构;
(2)多晶体:举例、特性,微观结构;
(3)非晶体:举例、特性。
气体、固体与液体
1.气体的状态参量
2.气体实验定律
3.固体
4.液体
(1)液体的表面张力:成因、方向、效果;
(2)浸润和不浸润:现象、成因;
(3)毛细现象:现象、成因、应用;
(4)液晶“三态”。
一、知识结构
1.体积 V:容器的容积。要用几何关系确定。
单位m3,L、mL等, 1L=103mL =10-3m3
2.压强 p:由大量气体分子对器壁的碰撞引起。
单位Pa(帕),1atm=1.01×105Pa=76cmHg
影响因素:温度(气体分子热运动的平均动能)、体积(分子数密度);
计算方法:根据动力学方程确定、根据连能管原理确定等。
3.热力学温度T :分子热运动平均动能的标志。
单位K(开) ,热学基本单位, T = t + 273 K,ΔT= Δt
测温原理:热平衡定律—若两个系统分别与第三个系统达到热平衡,那么这两个系统彼此之间也必定处于热平衡。
处于热平衡的两个系统必定具有相同的温度。
p2=40atm
V2=48mL
t2=941K(668oC)
气体溢出时,想象它的体积”增大”
二、应用与体会:描述气体状态的参量
例2.写出下列各段封闭气体的压强或压强关系
大气压强p0=75.0cmHg
pB=pA+ρgh
(P42NO.1)例1. 在完全失重的情况下气体对器壁是否还有压强?为什么?请设计实验验证你的猜想。
大气压强p0=1.00×105Pa
m1=2.50kg,
s1=80.0cm2
m2=1.50kg,
s2=40.0cm2
l=40.0cm
解:有。气体压强是气体分子频繁碰撞容器壁产生的,它与气体是否失重无关,完全失重时气体对器壁仍有压强。
打足气的篮球在自由下落过程中不会被大气压瘪。
p左= p0 = 75.0cmHg
p右= p左+15.0cmHg = 90.0cmHg
p0(s1-s2) +(m1+ m2)g = p(s1-s2)
解出 p=1.1×105Pa
(P43NO.2)例3.超市中有一种“强力吸盘挂钩”如图所示。下图是它的工作原理示意图。使用时, 按住锁扣把吸盘紧压在墙上(图甲),吸盘中的空气被挤出一部分。然后要把锁扣扳下(图乙),让锁扣以盘盖为依托把吸盘向外拉出。在拉起吸盘的同时,锁扣对盘盖施加压力, 致使盘盖以很大的压力压住吸盘。为什么锁扣 扳下后,盘盖对吸盘会产生很大的压力?
解:扳下锁扣,外拉吸盘,其中气体体积变大、压强减小。
松手后吸盘内压强小于大气压,大气压使盘盖紧压到吸盘边缘,防止空气渗入。
1.气体实验定律
(1)玻意耳定律:某种气体的质量和温度一定时,p1V1=p2V2;
(2)查理定律:某种气体的质量和体积一定时, ;
(3)盖-吕萨克定律:某种气体的质量和压强一定时, 。
2.图像:等温线、等容线、等压线在不同图像上形态不同。
3.微观解释要点:
(1)温度是分子平均动能的标志;
(2)压强由分子热运动平均动能(T)、分子数密度(m、V) 决定。
二、应用与体会:气体实验定律及解释
(P29倒二段)例1. 试用分子动理论定性解释盖-吕萨克定律。
解:一定质量的某种理想气体,温度升高时,分子的平均动能增大;只有气体的体积同时增大,使分子的数密度减小,才能保持压强不变。这就是盖-吕萨克定律的微观解释。
(P25NO.1)例2. 在做“探究气体等温变化的规律”的实 验中,实验小组记录了一系列数据。但是,仅就以下表中的两组数据来看,小王和小李却有完全不同的看法:小王认为,这两组数据很好 地体现了 p 跟 V 成反比的规律,因为两组数据 p 和 V 的乘积几乎相等;小李却认为,如果把这两组数据在纵坐标轴为 p、横坐标轴为 的坐标系中描点,这两点连线的延长线将不经过坐标原点,因此这两组数据没有反映 p 跟 V 成 反比的规律。对此你有什么看法?
解:小李的说法正确。
因为数据变化量太小,即使实验误差很大,pV 乘积也不会有大的变化,看起来相等 。
应该比较Δp与ΔV 的数据,而作p- 图时,两点连线的斜率描述的就是变化量的关系。若图线不过原点则没有体现 p 跟 V 成反比的规律。
(P42NO.6)例3. 在一次科学晚会上,胡老师表演了一 个“马德堡半球实验”。他先取出两个在碗底各 焊接了铁钩的不锈钢碗,在一个碗里烧了一些纸,然后迅速把另一个碗扣上,再在碗的外面 浇水,使其冷却到环境温度。用两段绳子分别 钩着铁钩朝相反的方向拉,试图把两个碗拉开 。当两边的人各增加到 5 人时,才把碗拉开。已知碗口的直径为 20 cm,环境温度 为 15 ℃,实验过程中碗不变形,也不漏气,设 每人平均用力为 200 N。请你估算一下,两个不锈钢碗刚被扣上时,里面空气的温度是多少?
p
5F
p0
解:对一个碗受力平衡时,
p0S = pS + 5F
碗口圆面积 S=π
碗内气体等容变化,
p1=p0=1.00×105Pa,T1 = t +273K;
p2=p,T2 = (15 +273)K。
由查理定律,
代入数据解出 t =150.5 ℃
例4.如图所示,水平放置的汽缸内壁光滑,活塞厚度不计,在A、B两处设有限制装置,使活塞只能在A、B之间运动,B左面汽缸的容积为V0,A、B之间的容积为0.1V0。开始时活塞在B处,缸内气体的压强为0.9p0(p0为大气压强),温度为297K。现缓慢加热汽缸内气体,直至399.3 K。求:
(1)活塞刚离开B处时的温度TB;
(2)缸内气体最后的压强p;
(3)在图中画出整个过程的p-V图线。
p1=0.9p0
T0=297K
p2=p0
TB=
p3=p0
TA=
解:(1)等容过程,由查理定律有
解得TB=330K
(2)活塞刚到A温度TA,等压过程,由盖—吕萨克定律有
p=
T=399.3K
,解得TA=363K
因TA<399.3K,故气体还要做等容变化。
,解得p =1.1p0
(3)如图。
小结:用气体定律分析问题的一般步骤
(1)确定研究对象;
等质量的气体或活塞、液柱等封闭物。
(2)写出或表达气体的状态参量;
写数值或表达式,协调压强单位;分析几何关系和受力时要仔细。
(3)根据状态变化过程的特点,列出方程式;
准确建模:用哪个或联用多个气体定律列式。
(4) 求解未知量,审核结果。
联立方程:定律的、几何的、力学的等等。
分类 晶体
非晶体
单晶体 多晶体
实例 石英、云母、食盐 金属、蔗糖 玻璃、松香、橡胶
外形 规则 不规则
熔点 确定 不确定
物理性质 各向异性 各向同性
微观结构 原子规则排列 晶粒杂乱无章排列 原子不规则排列
联系 1.多晶体由单晶体组成; 2.同一原子可构成不同结构的晶体,如石墨和金刚石; 3.晶体和非晶体可相互转化,如石英晶体和石英玻璃。
二、应用与体会:固体的分类及特性比较
(P35NO.1)例1. 某人为了检验一块薄片物质是否为晶体, 做了一个实验。他以薄片的正中央O为坐标原 点,建立Oxy平面直角坐标系,在两个坐标轴 上分别取两点x1和y1,使x1和y1到O点的距离相等。在x1和y1上分别固定一个测温元件,再把一个针状热源放在O点,发现x1点和y1点的温度在缓慢升高,但两点温度的高低没有差异。 于是得出结论:这块薄片是非晶体。
请说明:以上结论科学吗?为什么?
解:不科学。该薄片不一定是晶体,也可能是多晶体。此外,两个特定方向的同性,并不能说明各个方向都同性。
位置 分子力特性 宏观表现
表面层 液体与气体接触的液体薄层 引力 表面张力。使液体表面收缩至最小。
附着层 液体与固体接触的液体薄层 引力或斥力 表面收缩时为不浸润;表面扩展时为浸润。
浸润液体在细管中上升、不浸润液体在细管中下降,称毛细现象。
(P41NO.4)例2.要想把凝固在衣料上的蜡迹去掉,可以把两层棉纸分别放在蜡迹处衣服的上面和下面,然后用热熨斗在棉纸上来回烫熨。为什么这样做可以去掉衣料上的蜡迹?
答:棉纸内有很多细小的孔道起着毛细管的作用,当蜡受热熔化成液体后,由于毛细现象,它们会被棉纸吸走。
二、应用与体会:液体的表面张力和毛细现象
总 结
1.气体实验定律的表述、公式、图像及微观解释
(1)正确理解(三个前提条件)、准确记忆(名称不乱、图形精准等);
(2)盖-吕萨克定律的微观解释(逻辑关系及措辞)。
2.主要问题类型
(1)压强的计算;
(2)实验定律的选用;
(3)气体状态的图像分析及转换;
(4)固体和液体的相关概念辨析。
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
