北师大版七年级数学下册 5.3 简单轴对称图形 课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 5.3 简单轴对称图形 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
等腰三角形
学习目标
探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.
等腰三角形是生活中常见的图形.
(1)等腰三角形是轴对称图形吗?
如果是,请找出它的对称轴.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗?
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗?
底边上的高所在的直线呢?
(4)沿对称轴对折,你能发现等腰三角形的哪些特征?
说说你的理由.
D
A
B
C
想一想:
A
B
C
D
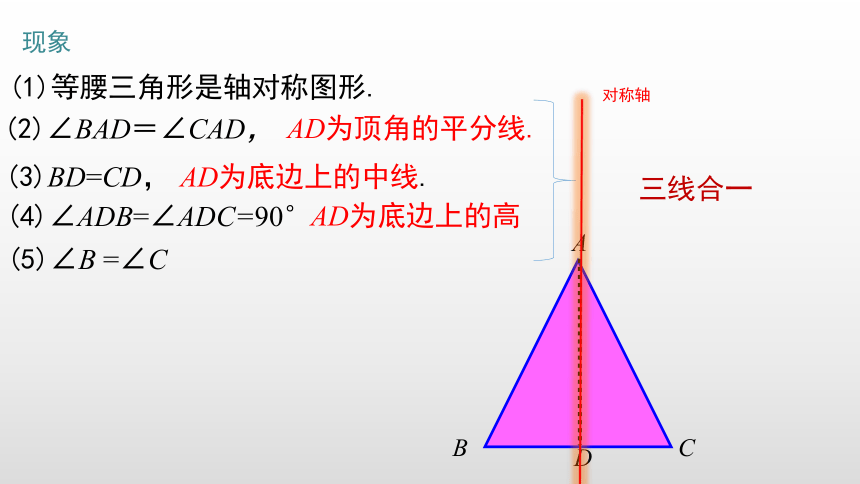
现象
(1)等腰三角形是轴对称图形.
(2)∠BAD=∠CAD,
(3)BD=CD,
(4)∠ADB=∠ADC=90°
(5)∠B =∠C
三线合一
AD为顶角的平分线.
AD为底边上的中线.
AD为底边上的高
对称轴
等腰三角形是轴对称图形.
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).所在的直线都是等腰三角形的对称轴.
归纳总结
等腰三角形的两个底角相等.
三线合一
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,在沿折痕剪开.
你有哪些办法可以得到一个等腰三角形?与同伴交流.
议一议
2.你能尝试用圆规吗?
1
墙上钉了一根木条,小明想检验这根木条是否水平. 他拿来一个如图所示的测平 仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点. 如果重锤过A
点,那么这根木条就
是水平的. 你能说明其
中的道理吗?
1、若等腰三角形的一个顶角为 40°,则它的另外两个内角为__________________
2、 若等腰三角形的一个底角为40°,则它的另外两个内角为______
70°,70° °
40°,100°
3、若等腰三角形的一个内角为 40°,则它的另外两个内角为__________________
4、 若等腰三角形的一个内角为120°,则它的另外两个内角为______
70°,70°或40°,100 °
30°,30°
一等腰三角形的两边长为2和4,则该等腰三角形的周长为________
一等腰三角形的两边长为3和4,则该等腰三角形的周长为________
10
10或11
如图,P,Q是△ABC边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数。
A
P
B
C
Q
开动脑筋
某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
请你出谋划策
)
)
)
对称点1
对称点2
对称点3
课后作业
见本课时练习
谢谢!
等腰三角形
学习目标
探索并掌握等腰三角形的轴对称性及其相关性质,能初步运用其解决有关问题.
等腰三角形是生活中常见的图形.
(1)等腰三角形是轴对称图形吗?
如果是,请找出它的对称轴.
(2)等腰三角形顶角平分线所在的直线是它的对称轴吗?
(3)等腰三角形底边上的中线所在的直线是它的对称轴吗?
底边上的高所在的直线呢?
(4)沿对称轴对折,你能发现等腰三角形的哪些特征?
说说你的理由.
D
A
B
C
想一想:
A
B
C
D
现象
(1)等腰三角形是轴对称图形.
(2)∠BAD=∠CAD,
(3)BD=CD,
(4)∠ADB=∠ADC=90°
(5)∠B =∠C
三线合一
AD为顶角的平分线.
AD为底边上的中线.
AD为底边上的高
对称轴
等腰三角形是轴对称图形.
等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”).所在的直线都是等腰三角形的对称轴.
归纳总结
等腰三角形的两个底角相等.
三线合一
等边三角形的性质:
1.等边三角形是轴对称图形。
2.等边三角形每个角的平分线和这个角的对 边上的中线、高线重合(“三线合一”),它们所在的直线都是等边三角形的对称轴。等边三角形共有三条对称轴。
3.等边三角形的各角都相等,都等于60°
1.按下面的步骤做一做:
(1)将长方形纸片对折
(2)然后沿对角线折叠,在沿折痕剪开.
你有哪些办法可以得到一个等腰三角形?与同伴交流.
议一议
2.你能尝试用圆规吗?
1
墙上钉了一根木条,小明想检验这根木条是否水平. 他拿来一个如图所示的测平 仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点. 如果重锤过A
点,那么这根木条就
是水平的. 你能说明其
中的道理吗?
1、若等腰三角形的一个顶角为 40°,则它的另外两个内角为__________________
2、 若等腰三角形的一个底角为40°,则它的另外两个内角为______
70°,70° °
40°,100°
3、若等腰三角形的一个内角为 40°,则它的另外两个内角为__________________
4、 若等腰三角形的一个内角为120°,则它的另外两个内角为______
70°,70°或40°,100 °
30°,30°
一等腰三角形的两边长为2和4,则该等腰三角形的周长为________
一等腰三角形的两边长为3和4,则该等腰三角形的周长为________
10
10或11
如图,P,Q是△ABC边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数。
A
P
B
C
Q
开动脑筋
某开发区新建了两片住宅区:A区、B区(如图).现在要从煤气主管道的一个地方建立一个接口,同时向这两个小区供气.请问,这个接口应建在哪,才能使得所用管道最短
A小区
B 小区
煤气主管道
请你出谋划策
)
)
)
对称点1
对称点2
对称点3
课后作业
见本课时练习
谢谢!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
