苏科版八年级数学下册 11.3 用反比例函数解决问题 课件(共15张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 11.3 用反比例函数解决问题 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 23:11:21 | ||
图片预览


文档简介
(共15张PPT)
11.3 用反比例函数解决问题
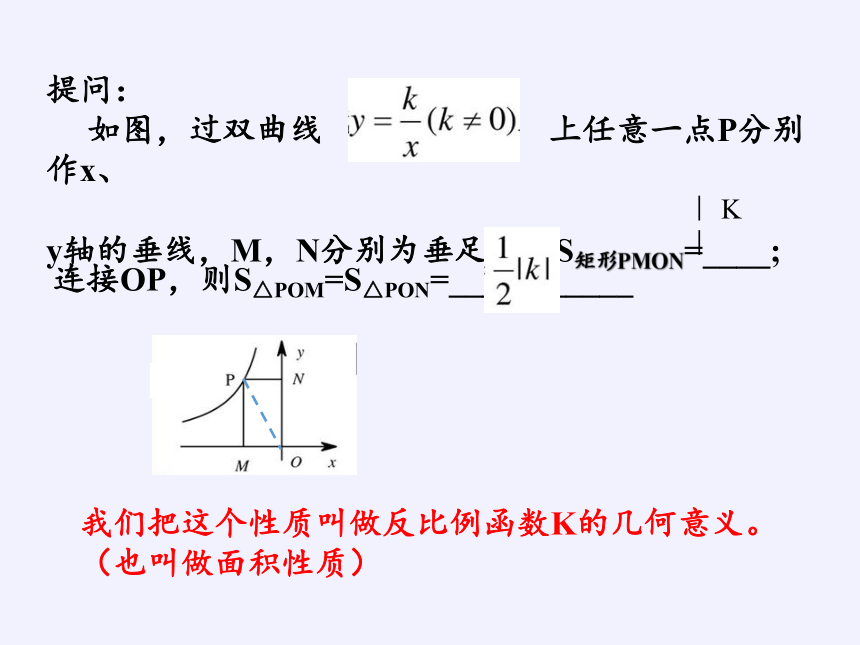
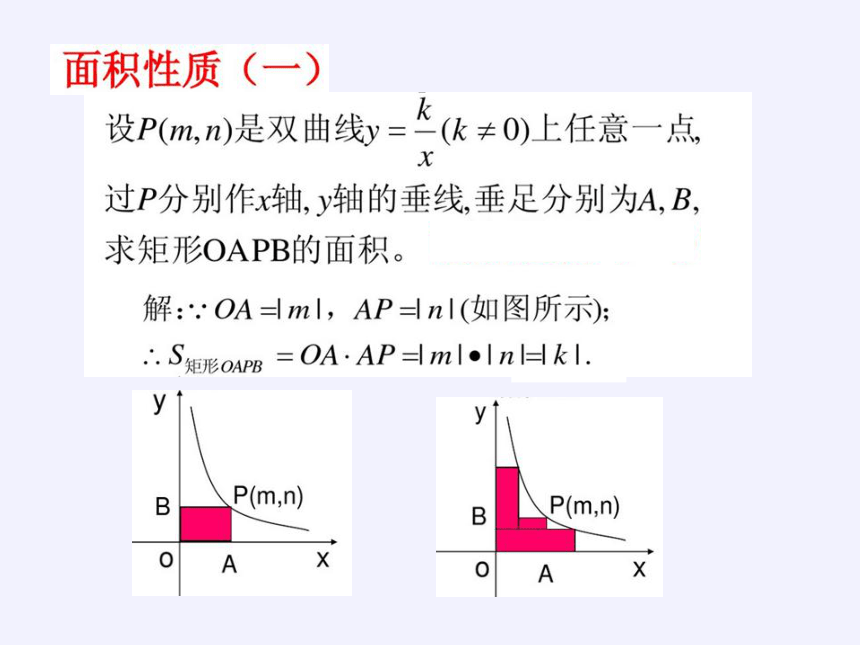
提问:
如图,过双曲线 上任意一点P分别作x、
y轴的垂线,M,N分别为垂足,则S矩形PMON=____;
︱ K ︱
连接OP,则S△POM=S△PON=___________
我们把这个性质叫做反比例函数K的几何意义。
(也叫做面积性质)
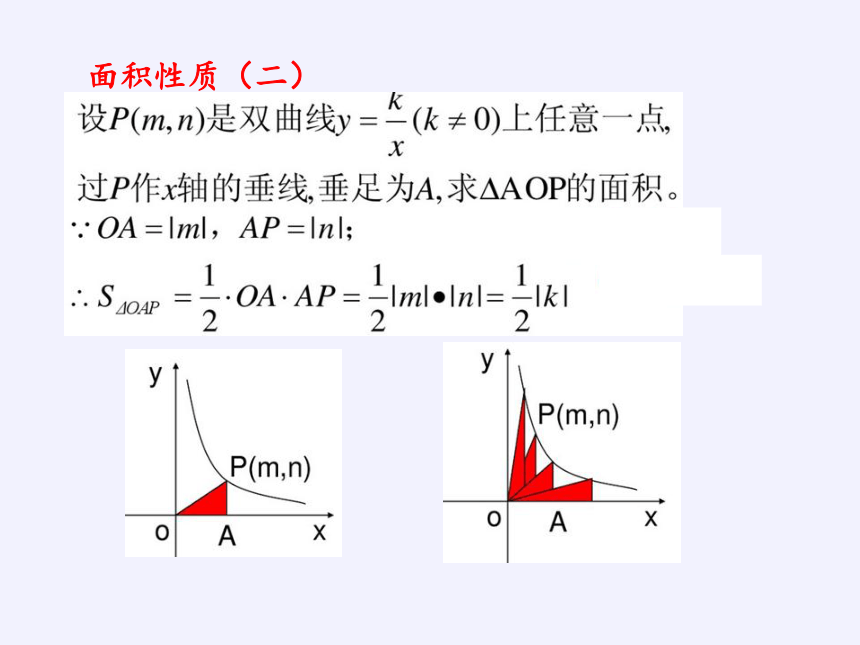
面积性质(二)
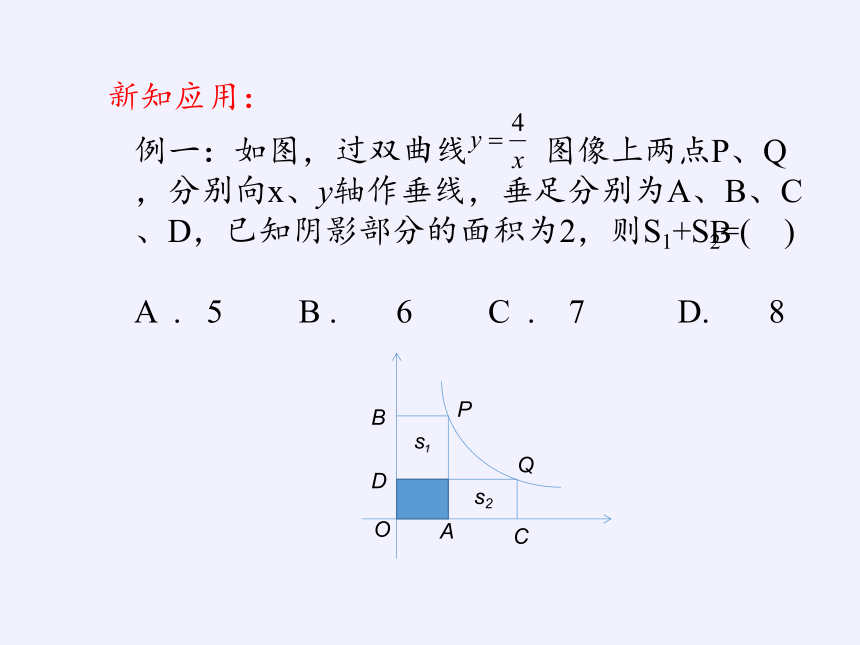
新知应用:
例一:如图,过双曲线 图像上两点P、Q,分别向x、y轴作垂线,垂足分别为A、B、C、D,已知阴影部分的面积为2,则S1+S2=( )
A . 5 B . 6 C . 7 D. 8
P
Q
A
C
O
D
B
s1
s2
B
新知应用:
例二:如图是反比例函数 和 (k1A.1 B.2 C.4 D.8
C
基础巩固:
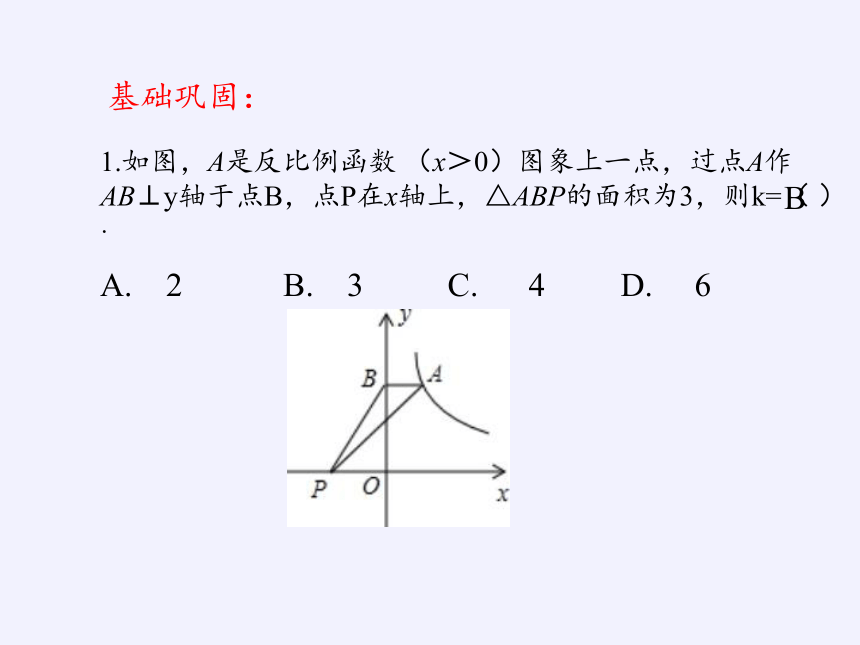
1.如图,A是反比例函数 (x>0)图象上一点,过点A作
AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则k=( ).
A. 2 B. 3 C. 4 D. 6
B
基础巩固:
2.如图,在反比例函数 的图象上,有点 ,它们的
横坐标依次为1,2,3,4.分别过这些点作 轴与 轴的
垂线,图中所构成的阴影部分的面积从左到右依次为
S1、S2、S3、S4,则 S1+S2+S3=( )
A. 3 B. 3.5 C. 2 D. 2.5
A
综合应用:
例三:如图,反比例函数 (x>0)的图象经过矩形
OABC对角线的交点M,分别于AB、BC交于点D、E,
若四边形ODBE的面积为12,则k的值为 ( )
A. 6 B. 4 C. 3 D. 2
B
综合应用:
3.如图,直线y=-2x+2与x轴y轴分别相交于点A、B,
四边形ABCD是正方形,曲线 在第一象限经过点D.则k=( )
A. 6 B. 4 C. 3 D. 2
A
综合应用:
4.如图,已知双曲线 (x>0)经过直角三角形OAB
斜边OB的中点D,与直角边AB相交于点C,若△OBC的面
积为3.则k的值为( ).
A
x
D
C
B
O
y
A. 5 B. 2 C. 3 D. 1
D
拓展延伸:
已知点A、B分别是 x轴、 y轴上的动点,点C、D是某个函数图像
上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形
时,称这个正方形为此函数图像的伴侣正方形。例如:如图(1),
正方形ABCD是一次函数 图像的其中一个伴侣正方形。若某函数
是反比例函数 如图(2)它的图像的伴侣正方形为
ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
y
x
A
B
O
D
C
D
y
O
x
2
课堂小结:
谈谈你本节课的收获:
再见!
拓展延伸:
一次函数y=ax+b的图像分别与x轴、y轴交于点M,N,与反比例函数 的图像相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C、E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F、D,AC与BD交于点K,连接CD.
(1)若点A、B在反比例函数 的图像的同一分支上,
如图1,试证明:①S四边形AEDK=S四边形CFBK;②AN=BM.
(2)若点A,B分别在反比例函数 的图像的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论.
谢 谢
11.3 用反比例函数解决问题
提问:
如图,过双曲线 上任意一点P分别作x、
y轴的垂线,M,N分别为垂足,则S矩形PMON=____;
︱ K ︱
连接OP,则S△POM=S△PON=___________
我们把这个性质叫做反比例函数K的几何意义。
(也叫做面积性质)
面积性质(二)
新知应用:
例一:如图,过双曲线 图像上两点P、Q,分别向x、y轴作垂线,垂足分别为A、B、C、D,已知阴影部分的面积为2,则S1+S2=( )
A . 5 B . 6 C . 7 D. 8
P
Q
A
C
O
D
B
s1
s2
B
新知应用:
例二:如图是反比例函数 和 (k1
C
基础巩固:
1.如图,A是反比例函数 (x>0)图象上一点,过点A作
AB⊥y轴于点B,点P在x轴上,△ABP的面积为3,则k=( ).
A. 2 B. 3 C. 4 D. 6
B
基础巩固:
2.如图,在反比例函数 的图象上,有点 ,它们的
横坐标依次为1,2,3,4.分别过这些点作 轴与 轴的
垂线,图中所构成的阴影部分的面积从左到右依次为
S1、S2、S3、S4,则 S1+S2+S3=( )
A. 3 B. 3.5 C. 2 D. 2.5
A
综合应用:
例三:如图,反比例函数 (x>0)的图象经过矩形
OABC对角线的交点M,分别于AB、BC交于点D、E,
若四边形ODBE的面积为12,则k的值为 ( )
A. 6 B. 4 C. 3 D. 2
B
综合应用:
3.如图,直线y=-2x+2与x轴y轴分别相交于点A、B,
四边形ABCD是正方形,曲线 在第一象限经过点D.则k=( )
A. 6 B. 4 C. 3 D. 2
A
综合应用:
4.如图,已知双曲线 (x>0)经过直角三角形OAB
斜边OB的中点D,与直角边AB相交于点C,若△OBC的面
积为3.则k的值为( ).
A
x
D
C
B
O
y
A. 5 B. 2 C. 3 D. 1
D
拓展延伸:
已知点A、B分别是 x轴、 y轴上的动点,点C、D是某个函数图像
上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形
时,称这个正方形为此函数图像的伴侣正方形。例如:如图(1),
正方形ABCD是一次函数 图像的其中一个伴侣正方形。若某函数
是反比例函数 如图(2)它的图像的伴侣正方形为
ABCD,点D(2,m)(m <2)在反比例函数图像上,求m的值及反比例函数解析式;
y
x
A
B
O
D
C
D
y
O
x
2
课堂小结:
谈谈你本节课的收获:
再见!
拓展延伸:
一次函数y=ax+b的图像分别与x轴、y轴交于点M,N,与反比例函数 的图像相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C、E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F、D,AC与BD交于点K,连接CD.
(1)若点A、B在反比例函数 的图像的同一分支上,
如图1,试证明:①S四边形AEDK=S四边形CFBK;②AN=BM.
(2)若点A,B分别在反比例函数 的图像的不同分支上,如图2,则AN与BM还相等吗?试证明你的结论.
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
