北师大版数学七年级下册专题课堂——巧用轴对称的性质解决问题课件(共21张PPT)
文档属性
| 名称 | 北师大版数学七年级下册专题课堂——巧用轴对称的性质解决问题课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
第五章 生活中的轴对称
专题课堂 巧用轴对称的性质解决问题
等腰三角形的性质
【例1】 如图所示,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.
解:∵AB=AC,AE平分∠BAC,∴AE⊥BC,即∠AEC=90°,∵∠ADC+∠EDC=180°,∠ADC=130°,∴∠EDC=50°,∴∠ECD=90°-50°=40°,又∵CD平分∠ACB,∴∠ACB=80°,∴∠B=∠ACB=80°,∠BAC=180°-80°×2=20°
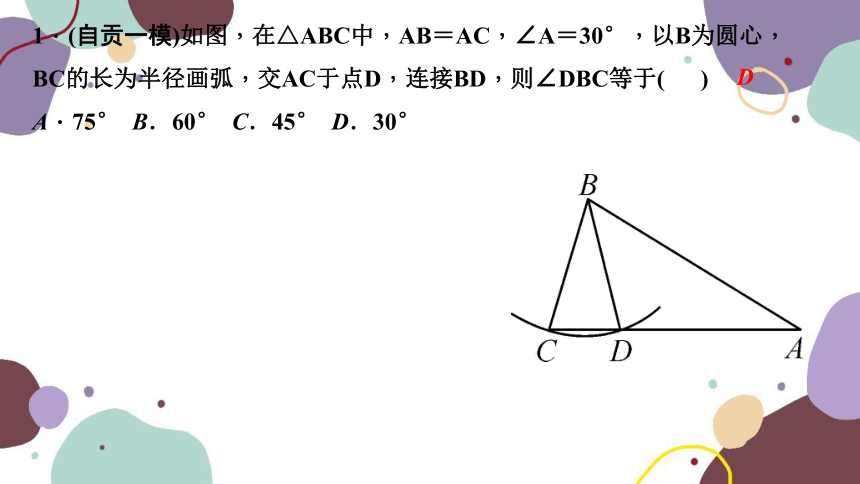
1.(自贡一模)如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠DBC等于( )
A.75° B.60° C.45° D.30°
D
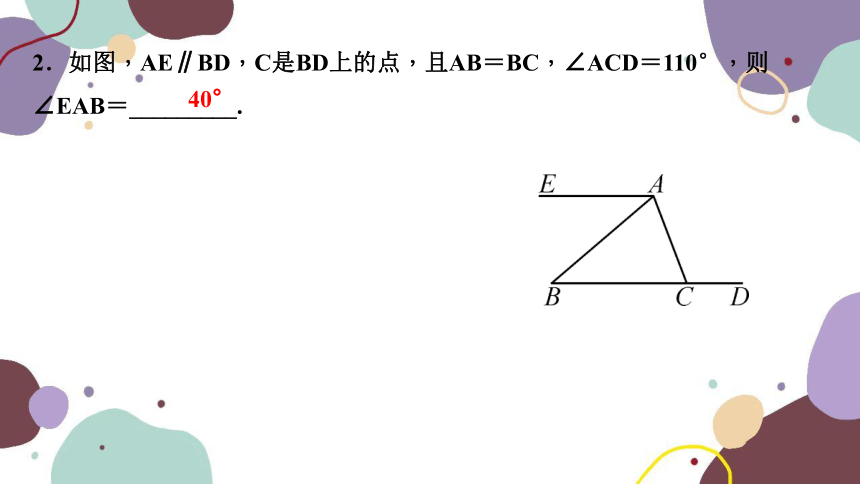
2.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=_________.
40°
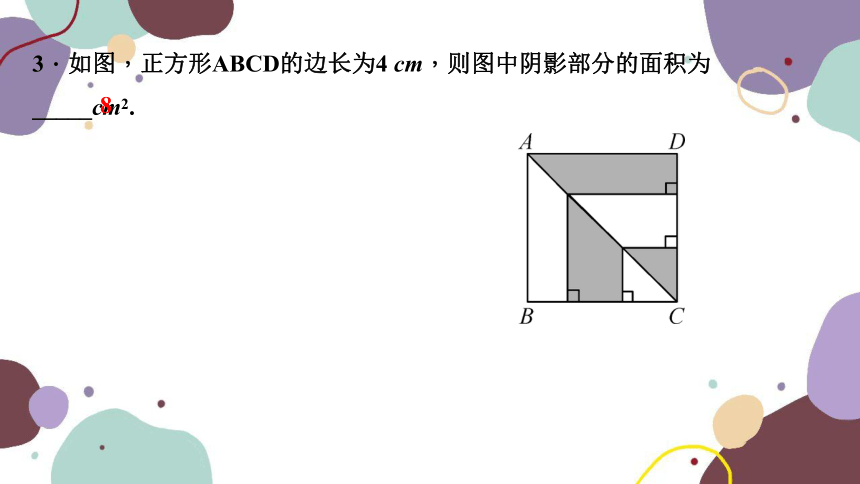
3.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为_____cm2.
8
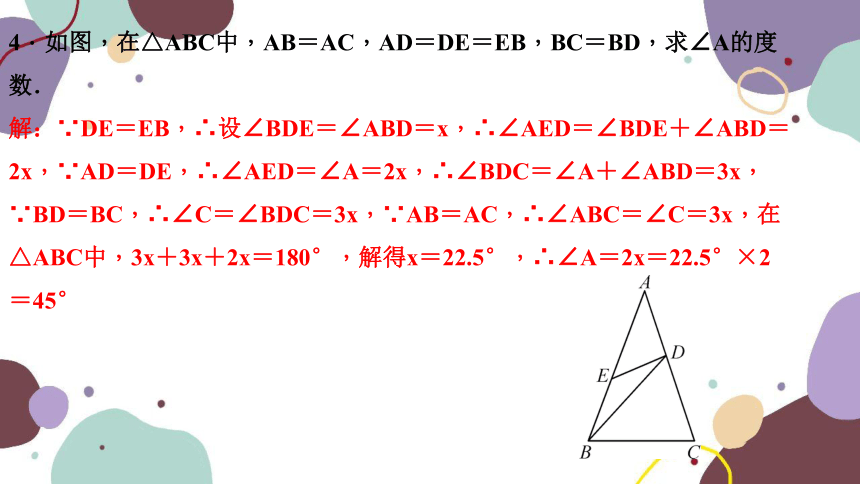
4.如图,在△ABC中,AB=AC,AD=DE=EB,BC=BD,求∠A的度数.
解:∵DE=EB,∴设∠BDE=∠ABD=x,∴∠AED=∠BDE+∠ABD=2x,∵AD=DE,∴∠AED=∠A=2x,∴∠BDC=∠A+∠ABD=3x,∵BD=BC,∴∠C=∠BDC=3x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,3x+3x+2x=180°,解得x=22.5°,∴∠A=2x=22.5°×2=45°
线段垂直平分线的性质
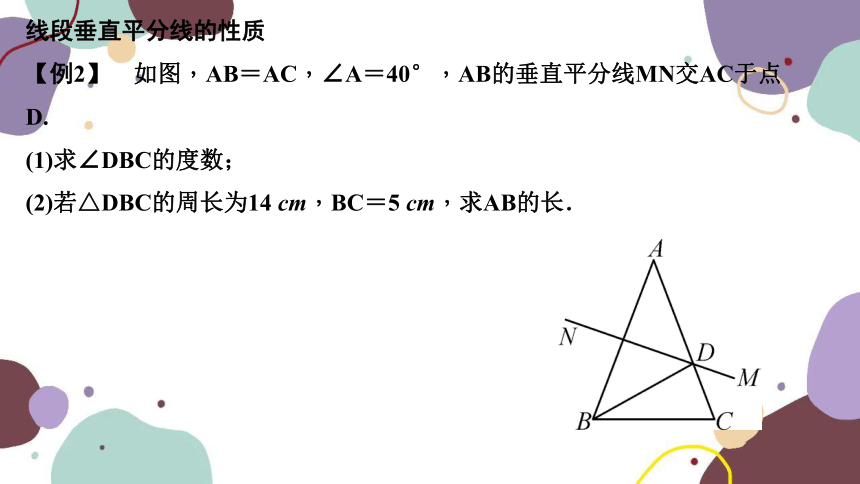
【例2】 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.
(1)求∠DBC的度数;
(2)若△DBC的周长为14 cm,BC=5 cm,求AB的长.
5.如图,在△ABC中,∠B=40°,AC的垂直平分线交AC于点D,交BC于点E,且∠EAB∶∠CAE=3∶1,则∠C等于_______.
28°
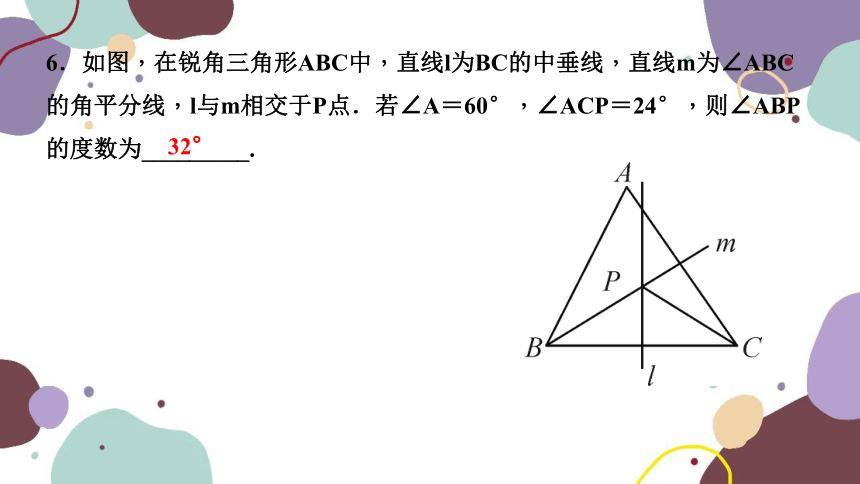
6.如图,在锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为_________.
32°
7.如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)若CE=4,△BDC的周长为18,求BD的长;
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
解:(1)∵MN垂直平分BC,∴DC=BD,CE=EB,又∵EC=4,∴BE=4,又∵△BDC的周长=18,∴BD+DC=10,∴BD=5
(2)∵∠ADM=60°,∴∠CDN=60°,又∵MN垂直平分BC,∴∠DEC=90°,∴∠C=30°,又∵∠C=∠DBC=30°,∠ABD=20°,∴∠ABC=50°,∴∠A=180°-∠C-∠ABC=100°
角平分线的性质
【例3】 如图,已知在Rt△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线.试说明:BC=2AB.
解:∵BD平分∠ABC,DA⊥AB,DE⊥BC,∴DA=DE,又∵∠DBA=∠DBE,∠A=∠DEB,
∴△ABD≌△EBD(AAS),
∴AB=BE,
∵DE是BC的垂直平分线,
∴BC=2BE=2AB
8.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5 B.PQ<5
C.PQ≥5 D.PQ>5
C
9.如图,在Rt△ABC中,∠ACB=90°,∠A=25°,D是AB上的一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于____________.
40°
10.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D.求证:
(1)ED=EC;
(2)∠ECD=∠EDC;
(3)射线OE与CD有什么关系?说明理由.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴EC=DE
(2)∵EC=DE,∴∠ECD=∠EDC
(3)OE是CD的垂直平分线.
理由:设OE,CD相交于点F.
∵∠ECD+∠OCF=∠EDC+∠ODF=90°,∠ECD=∠EDC,
∴∠ODF=∠OCF,∵∠DOF=∠COF,OF=OF.
∴△OCF≌△ODF,∴DF=CF,∠OFD=∠OFC=90°,∴OE是CD的垂直平分线
利用轴对称的性质解决路线最短问题
【例4】 如图,在铁路l的同侧有A,B两个工厂,要在铁路边修建一个货场C,货场应该建在什么地方,才能使A,B两厂到货场C距离之和最短?试画出图形.
解:如图所示,找到B点关于直线l的对称点B′,连接AB′交直线l于点C,则点C为所求货场位置
11.如图所示,牧童在A处放牧,其家在B处,A,B两点到河岸的距离分别AC和BD,且AC=BD.若点A到河岸CD中点M的距离为500 m,则牧童从A处牵牛到河边饮水再回家,最短路程为( )
A.7500 m B.1000 m
C.1500 m D.2000 m
B
12.如图,∠ABC内有一点P,在BA,BC边上各取一点P1,P2,求作△PP1P2,使△PP1P2的周长最小.
13.如图,已知牧马营地在P处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.
解:如图所示,最短路线为P→A→B→P
第五章 生活中的轴对称
专题课堂 巧用轴对称的性质解决问题
等腰三角形的性质
【例1】 如图所示,在△ABC中,AB=AC,∠BAC和∠ACB的平分线相交于点D,∠ADC=130°,求∠BAC的度数.
解:∵AB=AC,AE平分∠BAC,∴AE⊥BC,即∠AEC=90°,∵∠ADC+∠EDC=180°,∠ADC=130°,∴∠EDC=50°,∴∠ECD=90°-50°=40°,又∵CD平分∠ACB,∴∠ACB=80°,∴∠B=∠ACB=80°,∠BAC=180°-80°×2=20°
1.(自贡一模)如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径画弧,交AC于点D,连接BD,则∠DBC等于( )
A.75° B.60° C.45° D.30°
D
2.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=_________.
40°
3.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为_____cm2.
8
4.如图,在△ABC中,AB=AC,AD=DE=EB,BC=BD,求∠A的度数.
解:∵DE=EB,∴设∠BDE=∠ABD=x,∴∠AED=∠BDE+∠ABD=2x,∵AD=DE,∴∠AED=∠A=2x,∴∠BDC=∠A+∠ABD=3x,∵BD=BC,∴∠C=∠BDC=3x,∵AB=AC,∴∠ABC=∠C=3x,在△ABC中,3x+3x+2x=180°,解得x=22.5°,∴∠A=2x=22.5°×2=45°
线段垂直平分线的性质
【例2】 如图,AB=AC,∠A=40°,AB的垂直平分线MN交AC于点D.
(1)求∠DBC的度数;
(2)若△DBC的周长为14 cm,BC=5 cm,求AB的长.
5.如图,在△ABC中,∠B=40°,AC的垂直平分线交AC于点D,交BC于点E,且∠EAB∶∠CAE=3∶1,则∠C等于_______.
28°
6.如图,在锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠A=60°,∠ACP=24°,则∠ABP的度数为_________.
32°
7.如图,在△ABC中,BC边的垂直平分线交AC边于点D,连接BD.
(1)若CE=4,△BDC的周长为18,求BD的长;
(2)求∠ADM=60°,∠ABD=20°,求∠A的度数.
解:(1)∵MN垂直平分BC,∴DC=BD,CE=EB,又∵EC=4,∴BE=4,又∵△BDC的周长=18,∴BD+DC=10,∴BD=5
(2)∵∠ADM=60°,∴∠CDN=60°,又∵MN垂直平分BC,∴∠DEC=90°,∴∠C=30°,又∵∠C=∠DBC=30°,∠ABD=20°,∴∠ABC=50°,∴∠A=180°-∠C-∠ABC=100°
角平分线的性质
【例3】 如图,已知在Rt△ABC中,∠A=90°,BD是∠ABC的平分线,DE是BC的垂直平分线.试说明:BC=2AB.
解:∵BD平分∠ABC,DA⊥AB,DE⊥BC,∴DA=DE,又∵∠DBA=∠DBE,∠A=∠DEB,
∴△ABD≌△EBD(AAS),
∴AB=BE,
∵DE是BC的垂直平分线,
∴BC=2BE=2AB
8.点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )
A.PQ≤5 B.PQ<5
C.PQ≥5 D.PQ>5
C
9.如图,在Rt△ABC中,∠ACB=90°,∠A=25°,D是AB上的一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B′处,则∠ADB′等于____________.
40°
10.如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C,D.求证:
(1)ED=EC;
(2)∠ECD=∠EDC;
(3)射线OE与CD有什么关系?说明理由.
证明:(1)∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴EC=DE
(2)∵EC=DE,∴∠ECD=∠EDC
(3)OE是CD的垂直平分线.
理由:设OE,CD相交于点F.
∵∠ECD+∠OCF=∠EDC+∠ODF=90°,∠ECD=∠EDC,
∴∠ODF=∠OCF,∵∠DOF=∠COF,OF=OF.
∴△OCF≌△ODF,∴DF=CF,∠OFD=∠OFC=90°,∴OE是CD的垂直平分线
利用轴对称的性质解决路线最短问题
【例4】 如图,在铁路l的同侧有A,B两个工厂,要在铁路边修建一个货场C,货场应该建在什么地方,才能使A,B两厂到货场C距离之和最短?试画出图形.
解:如图所示,找到B点关于直线l的对称点B′,连接AB′交直线l于点C,则点C为所求货场位置
11.如图所示,牧童在A处放牧,其家在B处,A,B两点到河岸的距离分别AC和BD,且AC=BD.若点A到河岸CD中点M的距离为500 m,则牧童从A处牵牛到河边饮水再回家,最短路程为( )
A.7500 m B.1000 m
C.1500 m D.2000 m
B
12.如图,∠ABC内有一点P,在BA,BC边上各取一点P1,P2,求作△PP1P2,使△PP1P2的周长最小.
13.如图,已知牧马营地在P处,每天牧马人要赶着马群先到河边饮水,再带到草地吃草,然后回到营地,请你替牧马人设计出最短的放牧路线.
解:如图所示,最短路线为P→A→B→P
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
