人教版物理八年级下册同步提优训练 12.1杠杆 第3课时 杠杆的综合应用(有答案)
文档属性
| 名称 | 人教版物理八年级下册同步提优训练 12.1杠杆 第3课时 杠杆的综合应用(有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 211.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-28 13:09:03 | ||
图片预览


文档简介
第1节 杠杆
第3课时 杠杆的综合应用
1 单一杠杆类型的判断
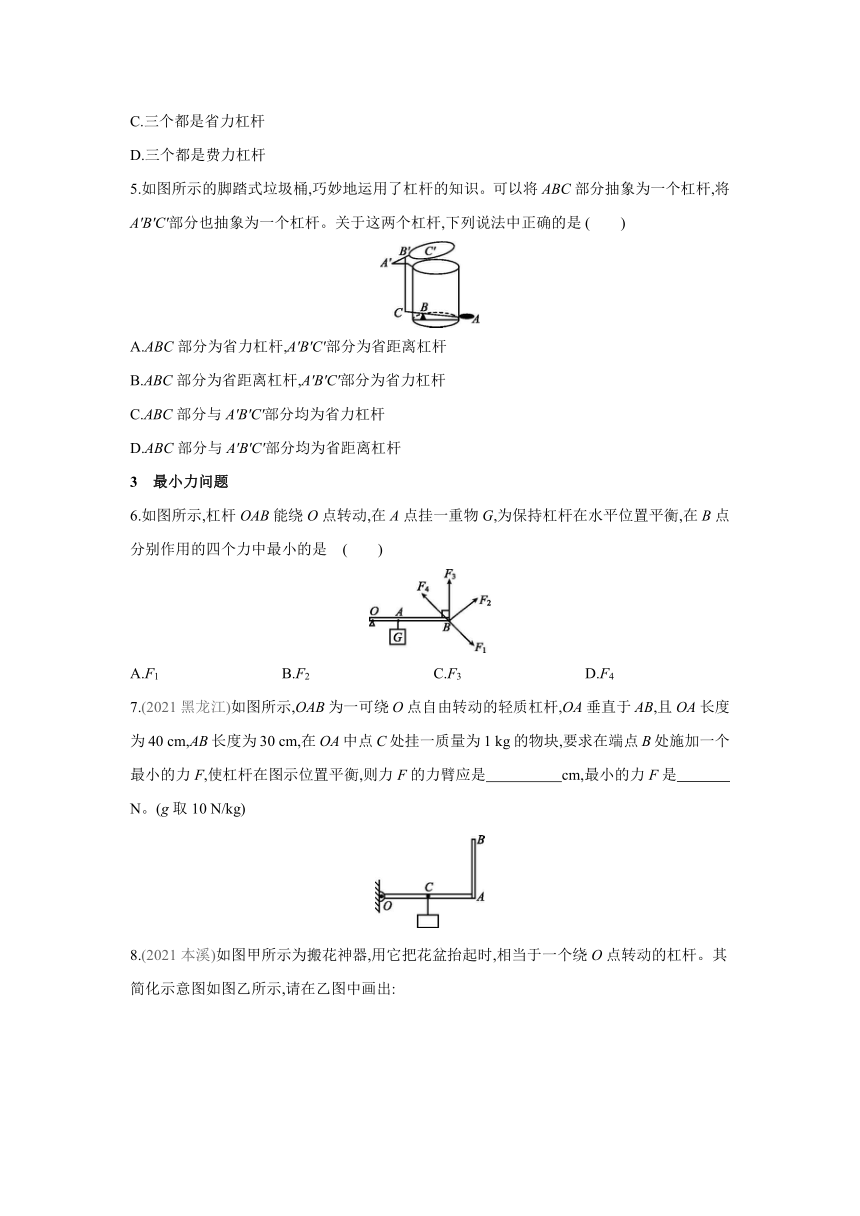
1.(2021深圳)如图所示杠杆中,属于费力杠杆的是 ( )
2.根据工作需要选择合适的工具是劳动者的基本技能。要剪断铁丝等较硬的物体,图中的四种剪刀应选择 ( )
3.踮脚是一项很好的有氧运动(如图所示),它简单易学,不受场地的限制,深受广大群众的喜爱,踮脚运动的基本模型是杠杆,下列分析正确的是 ( )
A.脚后跟是支点,是省力杠杆
B.脚后跟是支点,是费力杠杆
C.脚掌与地面接触的地方是支点,是省力杠杆
D.脚掌与地面接触的地方是支点,是费力杠杆
2 复合杠杆类型的判断
4.指甲刀是生活中常用的小工具,如图所示,它包含三个杠杆,下列关于这三个杠杆的说法正确的是 ( )
A.一个省力杠杆,两个费力杠杆
B.一个费力杠杆,两个省力杠杆
C.三个都是省力杠杆
D.三个都是费力杠杆
5.如图所示的脚踏式垃圾桶,巧妙地运用了杠杆的知识。可以将ABC部分抽象为一个杠杆,将A'B'C'部分也抽象为一个杠杆。关于这两个杠杆,下列说法中正确的是 ( )
A.ABC部分为省力杠杆,A'B'C'部分为省距离杠杆
B.ABC部分为省距离杠杆,A'B'C'部分为省力杠杆
C.ABC部分与A'B'C'部分均为省力杠杆
D.ABC部分与A'B'C'部分均为省距离杠杆
3 最小力问题
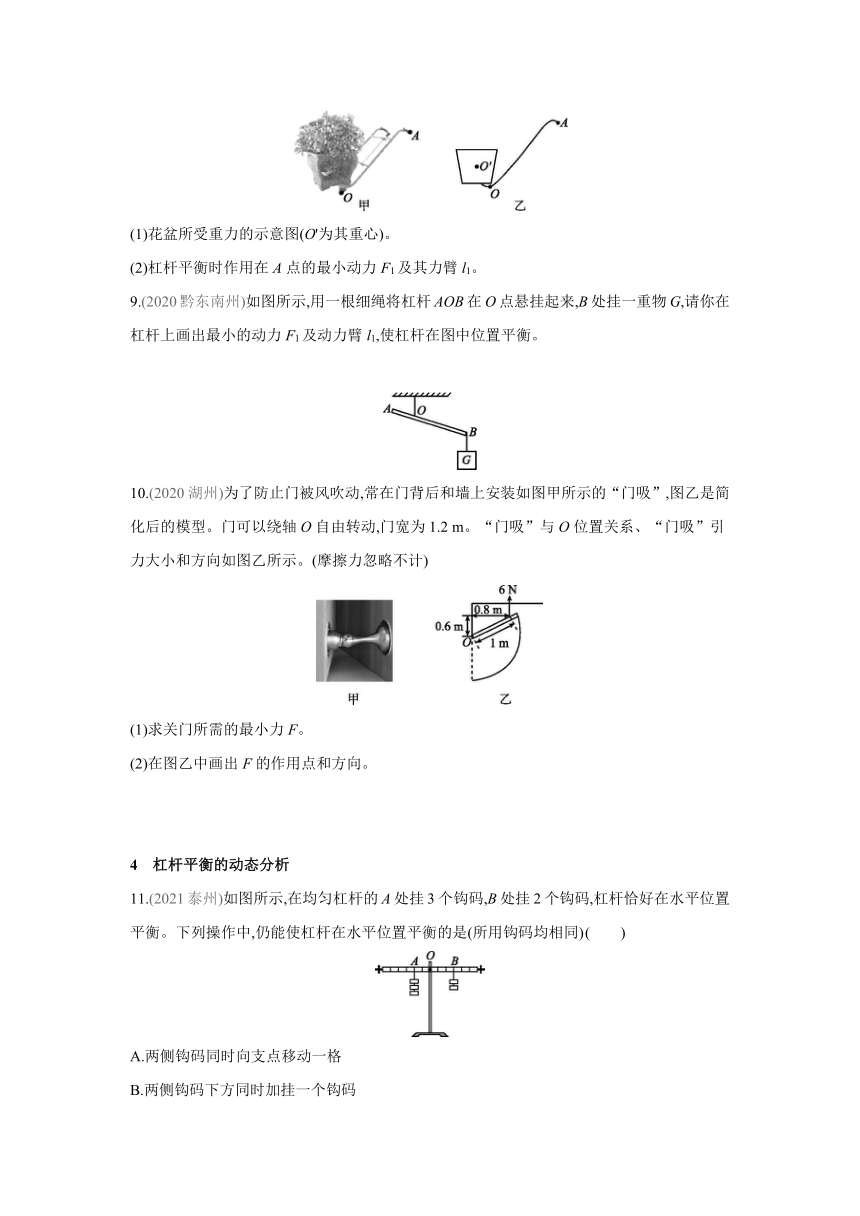
6.如图所示,杠杆OAB能绕O点转动,在A点挂一重物G,为保持杠杆在水平位置平衡,在B点分别作用的四个力中最小的是 ( )
A.F1 B.F2 C.F3 D.F4
7.(2021黑龙江)如图所示,OAB为一可绕O点自由转动的轻质杠杆,OA垂直于AB,且OA长度为40 cm,AB长度为30 cm,在OA中点C处挂一质量为1 kg的物块,要求在端点B处施加一个最小的力F,使杠杆在图示位置平衡,则力F的力臂应是 cm,最小的力F是 N。(g取10 N/kg)
8.(2021本溪)如图甲所示为搬花神器,用它把花盆抬起时,相当于一个绕O点转动的杠杆。其简化示意图如图乙所示,请在乙图中画出:
(1)花盆所受重力的示意图(O'为其重心)。
(2)杠杆平衡时作用在A点的最小动力F1及其力臂l1。
9.(2020黔东南州)如图所示,用一根细绳将杠杆AOB在O点悬挂起来,B处挂一重物G,请你在杠杆上画出最小的动力F1及动力臂l1,使杠杆在图中位置平衡。
10.(2020湖州)为了防止门被风吹动,常在门背后和墙上安装如图甲所示的“门吸”,图乙是简化后的模型。门可以绕轴O自由转动,门宽为1.2 m。“门吸”与O位置关系、“门吸”引力大小和方向如图乙所示。(摩擦力忽略不计)
(1)求关门所需的最小力F。
(2)在图乙中画出F的作用点和方向。
4 杠杆平衡的动态分析
11.(2021泰州)如图所示,在均匀杠杆的A处挂3个钩码,B处挂2个钩码,杠杆恰好在水平位置平衡。下列操作中,仍能使杠杆在水平位置平衡的是(所用钩码均相同) ( )
A.两侧钩码同时向支点移动一格
B.两侧钩码下方同时加挂一个钩码
C.左侧加挂一个钩码,右侧加挂两个钩码
D.左侧拿去一个钩码,右侧钩码向左移动一格
12.如图所示,杠杆在水平位置处于平衡状态,如果将物体A和B同时向靠近支点的方向移动相同的距离,下列判断正确的是 ( )
A.杠杆仍能平衡
B.杠杆不能平衡,左端下沉
C.杠杆不能平衡,右端下沉
D.无法判断杠杆的状态
13.(2020达州)一轻质不等臂杠杆AOB的左右两端分别吊着一实心铝块和铜块,此时杠杆在水平位置平衡。现将铝块、铜块同时浸没在水中,如图所示。已知ρ水=1.0×103 kg/m3,ρ铝=2.7×103 kg/m3,ρ铜=8.9×103 kg/m3,则下列判断正确的是 ( )
A.A端下降 B.B端下降
C.仍然平衡 D.无法判断
14.(2021新疆)如图所示,用剪刀将一张纸片缓慢地一刀剪断,在这个过程中阻力臂l阻和动力F动的变化情况是 ( )
A.l阻不变,F动变大
B.l阻不变,F动不变
C.l阻变大,F动变大
D.l阻变大,F动不变
15.如图所示,用一个始终水平向右的力F,把轻质杠杆OA从图示位置缓慢拉至水平位置的过程中,力F的大小将 ( )
A.变大 B.不变
C.变小 D.不能确定
16.如图所示,AB是能绕B点转动的轻质杠杆,在中点C处用绳子悬挂重为100 N的物体(不计绳重)。在A端施加竖直向上的拉力使杠杆在水平位置平衡,则拉力F= N。若保持拉力方向始终垂直于杠杆,将A端缓慢向上提升一小段距离,在提升的过程中,拉力F将
(选填“增大”“减小”或“不变”)。
17.一根粗细均匀的木棒,斜靠在竖直墙壁上。墙壁光滑,地面粗糙,木棒受到的重力为G,墙壁对木棒的弹力为F,如图所示,现让木棒的倾斜度变小一些至虚线所示位置,木棒仍能静止斜靠在墙上,则与原来相比,G ,F 。(均选填“变大”“变小”或“不变”)
18.用一根长为l、重为G0的均匀铁棒,插入一个边长为a、重为G的正方体物块的底部,在另一端施加一个向上的力,将物块撬起一个很小的角度,如图所示,图中的角度已被放大。若铁棒插入物块底部的长度为物块边长的三分之一,则要撬动物块,作用在铁棒最右端的力至少为( )
A.G0+ B.G0+
C.+ D.+
第1节 杠杆
第3课时 杠杆的综合应用
1.B 2.D
3.C 如图所示,踮脚时,脚掌与地面接触的地方是支点,小腿肌肉对脚的拉力向上,从图中可知动力臂大于阻力臂,是省力杠杆。
4.A
5.A 图中的ABC部分和A'B'C'部分都可以抽象为杠杆。ABC部分的B点为支点,A点为动力作用点,C点为阻力作用点,动力臂大于阻力臂,所以ABC部分为省力杠杆;A'B'C'部分的A'点为支点,B'点为动力作用点,C'点为阻力作用点,动力臂小于阻力臂,所以A'B'C'部分为省距离(费力)杠杆。
6.C 由杠杆平衡条件F1l1=F2l2可知,在阻力和阻力臂一定的情况下,动力臂越长,动力越小,F3对应的动力臂最长,所以F3最小。
7.50 4
在B点施加一个最小的力,则力臂应最长,当OB作为力臂时,动力臂是最大的,此时动力最小;OA=40 cm,AB=30 cm,根据勾股定理可知,OB==50 cm,OC=20 cm;根据杠杆的平衡条件可知:G×OC=F×OB,即mg×OC=F×OB,代入数据得:1 kg×10 N/kg×20 cm=F×50 cm,解得:F=4 N。
8.如图所示
9.如图所示
10.(1)由题知,关门的最大力臂为1.2 m,“门吸”引力的力臂为0.8 m。利用杠杆平衡条件可得,F×l门宽=F引力×l引力,即F×1.2 m=6 N×0.8 m,解得F=4 N。
(2)如图所示
11.D
12.C 原来杠杆在水平位置处于平衡状态,此时作用在杠杆上的力分别为物体A、B对杠杆的拉力,大小等于它们各自的重力,其对应的力臂分别为OC、OD(如图所示)。
根据杠杆的平衡条件可得:mAg×OC=mBg×OD,
由图示可知,OCmB。
当物体A、B同时向支点移动相同的距离ΔL时,两边的力臂都减小ΔL,此时左边的力和力臂的乘积为
mAg×(OC-ΔL)=mAg×OC-mAg×ΔL,
右边的力和力臂的乘积为
mBg×(OD-ΔL)=mBg×OD-mBg×ΔL,
由于mA>mB,所以mAg×ΔL>mBg×ΔL,
所以mAg×OC-mAg×ΔL因此杠杆将向悬挂B物体的一端即右端倾斜。
13.B 杠杆处于平衡状态,根据杠杆平衡条件得,
G铝×OA=G铜×OB,
ρ铝gV铝×OA=ρ铜gV铜×OB①,
因为ρ铝<ρ铜,
则V铝×OA>V铜×OB②,
现将铝块、铜块同时浸没在水中,由阿基米德原理得,
F浮=ρ水gV排=ρ水gV物,
故此时作用在杠杆左、右两端的力分别为
FA=ρ铝gV铝-ρ水gV铝,
FB=ρ铜gV铜-ρ水gV铜,
FA×OA-FB×OB=(ρ铝gV铝-ρ水gV铝)×OA-(ρ铜gV铜-ρ水gV铜)×OB=ρ铝gV铝×OA-ρ水gV铝×OA-ρ铜gV铜×OB+ρ水gV铜×OB,
由①知,FA×OA-FB×OB=ρ水gV铜×OB-ρ水gV铝×OA=ρ水g(V铜×OB-V铝×OA)③,
由②③知,FA×OA-FB×OB<0,
所以FA×OA14.C 剪刀的轴是支点,剪纸时阻力作用在纸和剪刀的接触点,用剪刀将一张纸片缓慢地一刀剪断的过程中,阻力F阻不变,动力臂l动不变,阻力臂l阻逐渐变大,由杠杆平衡条件:动力×动力臂=阻力×阻力臂可知,动力F动逐渐变大。
15.A 由题意可知:用一个始终水平向右的力F,把杠杆OA从图示位置缓慢拉至水平位置的过程中,阻力的大小(等于物体的重力G)不变,阻力臂变大,动力臂变小,根据杠杆平衡条件F1l1=F2l2可知,动力将变大。
16.50 减小 杠杆在水平位置保持平衡,由杠杆平衡条件F1l1=F2l2可得,拉力的大小:
F1=G=×100 N=50 N。
若将A端缓慢向上提升一小段距离,则阻力臂l2将变小,阻力G不变,即F2l2变小,因为拉力方向始终垂直于杠杆,所以动力臂l1不变,根据F1l1=F2l2可知,拉力F减小。
17.不变 变大
18.C 在阻力与阻力臂一定的情况下,由杠杆平衡条件可知,动力臂越大,动力越小,故当力F垂直于铁棒时,力F的力臂是铁棒的长度l,F的力臂最大,力F最小;铁棒重力的作用点在铁棒的重心,在铁棒的中点处,铁棒重力G0的力臂l2=,物体提供的阻力为,力臂l2'=;由杠杆平衡条件可得×+G0×=Fl,则F=+。
第3课时 杠杆的综合应用
1 单一杠杆类型的判断
1.(2021深圳)如图所示杠杆中,属于费力杠杆的是 ( )
2.根据工作需要选择合适的工具是劳动者的基本技能。要剪断铁丝等较硬的物体,图中的四种剪刀应选择 ( )
3.踮脚是一项很好的有氧运动(如图所示),它简单易学,不受场地的限制,深受广大群众的喜爱,踮脚运动的基本模型是杠杆,下列分析正确的是 ( )
A.脚后跟是支点,是省力杠杆
B.脚后跟是支点,是费力杠杆
C.脚掌与地面接触的地方是支点,是省力杠杆
D.脚掌与地面接触的地方是支点,是费力杠杆
2 复合杠杆类型的判断
4.指甲刀是生活中常用的小工具,如图所示,它包含三个杠杆,下列关于这三个杠杆的说法正确的是 ( )
A.一个省力杠杆,两个费力杠杆
B.一个费力杠杆,两个省力杠杆
C.三个都是省力杠杆
D.三个都是费力杠杆
5.如图所示的脚踏式垃圾桶,巧妙地运用了杠杆的知识。可以将ABC部分抽象为一个杠杆,将A'B'C'部分也抽象为一个杠杆。关于这两个杠杆,下列说法中正确的是 ( )
A.ABC部分为省力杠杆,A'B'C'部分为省距离杠杆
B.ABC部分为省距离杠杆,A'B'C'部分为省力杠杆
C.ABC部分与A'B'C'部分均为省力杠杆
D.ABC部分与A'B'C'部分均为省距离杠杆
3 最小力问题
6.如图所示,杠杆OAB能绕O点转动,在A点挂一重物G,为保持杠杆在水平位置平衡,在B点分别作用的四个力中最小的是 ( )
A.F1 B.F2 C.F3 D.F4
7.(2021黑龙江)如图所示,OAB为一可绕O点自由转动的轻质杠杆,OA垂直于AB,且OA长度为40 cm,AB长度为30 cm,在OA中点C处挂一质量为1 kg的物块,要求在端点B处施加一个最小的力F,使杠杆在图示位置平衡,则力F的力臂应是 cm,最小的力F是 N。(g取10 N/kg)
8.(2021本溪)如图甲所示为搬花神器,用它把花盆抬起时,相当于一个绕O点转动的杠杆。其简化示意图如图乙所示,请在乙图中画出:
(1)花盆所受重力的示意图(O'为其重心)。
(2)杠杆平衡时作用在A点的最小动力F1及其力臂l1。
9.(2020黔东南州)如图所示,用一根细绳将杠杆AOB在O点悬挂起来,B处挂一重物G,请你在杠杆上画出最小的动力F1及动力臂l1,使杠杆在图中位置平衡。
10.(2020湖州)为了防止门被风吹动,常在门背后和墙上安装如图甲所示的“门吸”,图乙是简化后的模型。门可以绕轴O自由转动,门宽为1.2 m。“门吸”与O位置关系、“门吸”引力大小和方向如图乙所示。(摩擦力忽略不计)
(1)求关门所需的最小力F。
(2)在图乙中画出F的作用点和方向。
4 杠杆平衡的动态分析
11.(2021泰州)如图所示,在均匀杠杆的A处挂3个钩码,B处挂2个钩码,杠杆恰好在水平位置平衡。下列操作中,仍能使杠杆在水平位置平衡的是(所用钩码均相同) ( )
A.两侧钩码同时向支点移动一格
B.两侧钩码下方同时加挂一个钩码
C.左侧加挂一个钩码,右侧加挂两个钩码
D.左侧拿去一个钩码,右侧钩码向左移动一格
12.如图所示,杠杆在水平位置处于平衡状态,如果将物体A和B同时向靠近支点的方向移动相同的距离,下列判断正确的是 ( )
A.杠杆仍能平衡
B.杠杆不能平衡,左端下沉
C.杠杆不能平衡,右端下沉
D.无法判断杠杆的状态
13.(2020达州)一轻质不等臂杠杆AOB的左右两端分别吊着一实心铝块和铜块,此时杠杆在水平位置平衡。现将铝块、铜块同时浸没在水中,如图所示。已知ρ水=1.0×103 kg/m3,ρ铝=2.7×103 kg/m3,ρ铜=8.9×103 kg/m3,则下列判断正确的是 ( )
A.A端下降 B.B端下降
C.仍然平衡 D.无法判断
14.(2021新疆)如图所示,用剪刀将一张纸片缓慢地一刀剪断,在这个过程中阻力臂l阻和动力F动的变化情况是 ( )
A.l阻不变,F动变大
B.l阻不变,F动不变
C.l阻变大,F动变大
D.l阻变大,F动不变
15.如图所示,用一个始终水平向右的力F,把轻质杠杆OA从图示位置缓慢拉至水平位置的过程中,力F的大小将 ( )
A.变大 B.不变
C.变小 D.不能确定
16.如图所示,AB是能绕B点转动的轻质杠杆,在中点C处用绳子悬挂重为100 N的物体(不计绳重)。在A端施加竖直向上的拉力使杠杆在水平位置平衡,则拉力F= N。若保持拉力方向始终垂直于杠杆,将A端缓慢向上提升一小段距离,在提升的过程中,拉力F将
(选填“增大”“减小”或“不变”)。
17.一根粗细均匀的木棒,斜靠在竖直墙壁上。墙壁光滑,地面粗糙,木棒受到的重力为G,墙壁对木棒的弹力为F,如图所示,现让木棒的倾斜度变小一些至虚线所示位置,木棒仍能静止斜靠在墙上,则与原来相比,G ,F 。(均选填“变大”“变小”或“不变”)
18.用一根长为l、重为G0的均匀铁棒,插入一个边长为a、重为G的正方体物块的底部,在另一端施加一个向上的力,将物块撬起一个很小的角度,如图所示,图中的角度已被放大。若铁棒插入物块底部的长度为物块边长的三分之一,则要撬动物块,作用在铁棒最右端的力至少为( )
A.G0+ B.G0+
C.+ D.+
第1节 杠杆
第3课时 杠杆的综合应用
1.B 2.D
3.C 如图所示,踮脚时,脚掌与地面接触的地方是支点,小腿肌肉对脚的拉力向上,从图中可知动力臂大于阻力臂,是省力杠杆。
4.A
5.A 图中的ABC部分和A'B'C'部分都可以抽象为杠杆。ABC部分的B点为支点,A点为动力作用点,C点为阻力作用点,动力臂大于阻力臂,所以ABC部分为省力杠杆;A'B'C'部分的A'点为支点,B'点为动力作用点,C'点为阻力作用点,动力臂小于阻力臂,所以A'B'C'部分为省距离(费力)杠杆。
6.C 由杠杆平衡条件F1l1=F2l2可知,在阻力和阻力臂一定的情况下,动力臂越长,动力越小,F3对应的动力臂最长,所以F3最小。
7.50 4
在B点施加一个最小的力,则力臂应最长,当OB作为力臂时,动力臂是最大的,此时动力最小;OA=40 cm,AB=30 cm,根据勾股定理可知,OB==50 cm,OC=20 cm;根据杠杆的平衡条件可知:G×OC=F×OB,即mg×OC=F×OB,代入数据得:1 kg×10 N/kg×20 cm=F×50 cm,解得:F=4 N。
8.如图所示
9.如图所示
10.(1)由题知,关门的最大力臂为1.2 m,“门吸”引力的力臂为0.8 m。利用杠杆平衡条件可得,F×l门宽=F引力×l引力,即F×1.2 m=6 N×0.8 m,解得F=4 N。
(2)如图所示
11.D
12.C 原来杠杆在水平位置处于平衡状态,此时作用在杠杆上的力分别为物体A、B对杠杆的拉力,大小等于它们各自的重力,其对应的力臂分别为OC、OD(如图所示)。
根据杠杆的平衡条件可得:mAg×OC=mBg×OD,
由图示可知,OC
当物体A、B同时向支点移动相同的距离ΔL时,两边的力臂都减小ΔL,此时左边的力和力臂的乘积为
mAg×(OC-ΔL)=mAg×OC-mAg×ΔL,
右边的力和力臂的乘积为
mBg×(OD-ΔL)=mBg×OD-mBg×ΔL,
由于mA>mB,所以mAg×ΔL>mBg×ΔL,
所以mAg×OC-mAg×ΔL
13.B 杠杆处于平衡状态,根据杠杆平衡条件得,
G铝×OA=G铜×OB,
ρ铝gV铝×OA=ρ铜gV铜×OB①,
因为ρ铝<ρ铜,
则V铝×OA>V铜×OB②,
现将铝块、铜块同时浸没在水中,由阿基米德原理得,
F浮=ρ水gV排=ρ水gV物,
故此时作用在杠杆左、右两端的力分别为
FA=ρ铝gV铝-ρ水gV铝,
FB=ρ铜gV铜-ρ水gV铜,
FA×OA-FB×OB=(ρ铝gV铝-ρ水gV铝)×OA-(ρ铜gV铜-ρ水gV铜)×OB=ρ铝gV铝×OA-ρ水gV铝×OA-ρ铜gV铜×OB+ρ水gV铜×OB,
由①知,FA×OA-FB×OB=ρ水gV铜×OB-ρ水gV铝×OA=ρ水g(V铜×OB-V铝×OA)③,
由②③知,FA×OA-FB×OB<0,
所以FA×OA
15.A 由题意可知:用一个始终水平向右的力F,把杠杆OA从图示位置缓慢拉至水平位置的过程中,阻力的大小(等于物体的重力G)不变,阻力臂变大,动力臂变小,根据杠杆平衡条件F1l1=F2l2可知,动力将变大。
16.50 减小 杠杆在水平位置保持平衡,由杠杆平衡条件F1l1=F2l2可得,拉力的大小:
F1=G=×100 N=50 N。
若将A端缓慢向上提升一小段距离,则阻力臂l2将变小,阻力G不变,即F2l2变小,因为拉力方向始终垂直于杠杆,所以动力臂l1不变,根据F1l1=F2l2可知,拉力F减小。
17.不变 变大
18.C 在阻力与阻力臂一定的情况下,由杠杆平衡条件可知,动力臂越大,动力越小,故当力F垂直于铁棒时,力F的力臂是铁棒的长度l,F的力臂最大,力F最小;铁棒重力的作用点在铁棒的重心,在铁棒的中点处,铁棒重力G0的力臂l2=,物体提供的阻力为,力臂l2'=;由杠杆平衡条件可得×+G0×=Fl,则F=+。
