人教版物理八年级下册同步提优训练 12.3机械效率 第2课时 机械效率的测量(有答案)
文档属性
| 名称 | 人教版物理八年级下册同步提优训练 12.3机械效率 第2课时 机械效率的测量(有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 176.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览


文档简介
第3节 机械效率
第2课时 机械效率的测量
1 测量滑轮组的机械效率
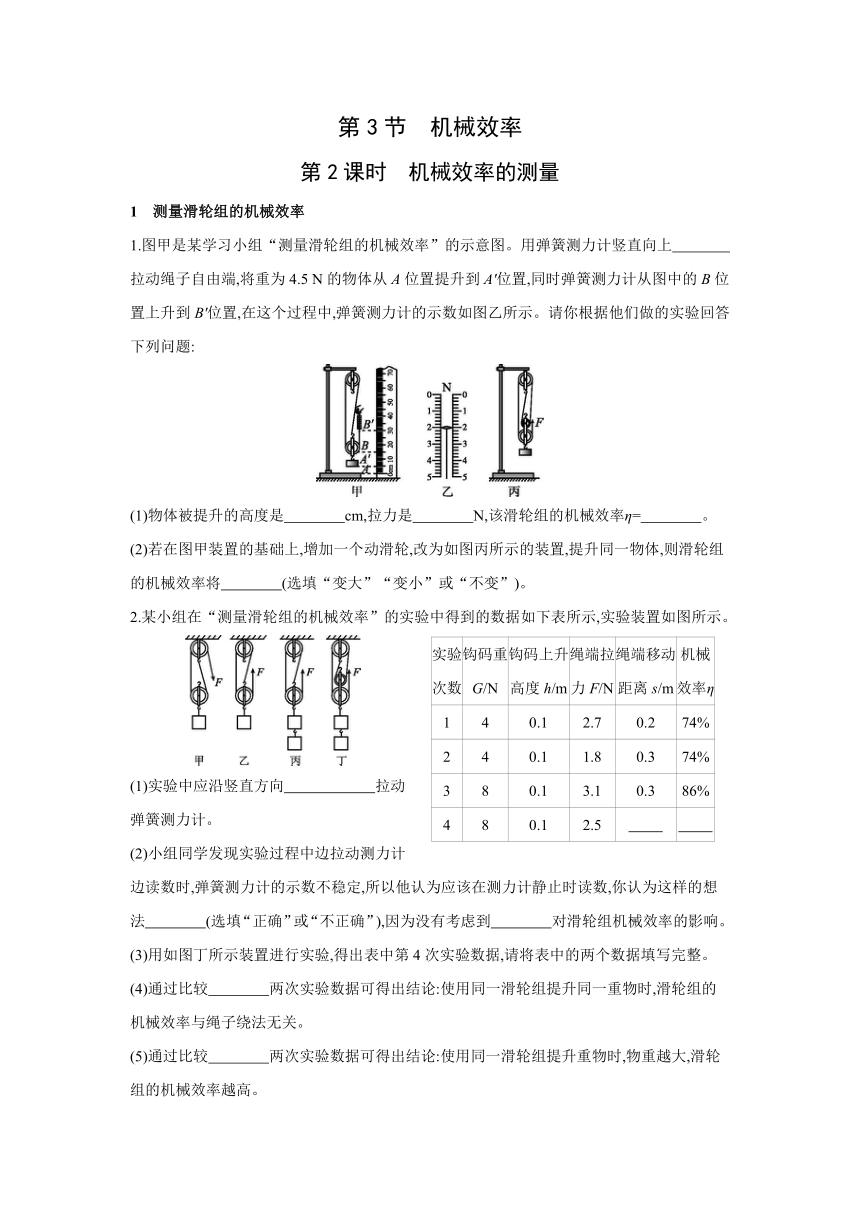
1.图甲是某学习小组“测量滑轮组的机械效率”的示意图。用弹簧测力计竖直向上 拉动绳子自由端,将重为4.5 N的物体从A位置提升到A'位置,同时弹簧测力计从图中的B位置上升到B'位置,在这个过程中,弹簧测力计的示数如图乙所示。请你根据他们做的实验回答下列问题:
(1)物体被提升的高度是 cm,拉力是 N,该滑轮组的机械效率η= 。
(2)若在图甲装置的基础上,增加一个动滑轮,改为如图丙所示的装置,提升同一物体,则滑轮组的机械效率将 (选填“变大”“变小”或“不变”)。
2.某小组在“测量滑轮组的机械效率”的实验中得到的数据如下表所示,实验装置如图所示。
实验 次数 钩码重 G/N 钩码上升 高度h/m 绳端拉 力F/N 绳端移动 距离s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5
(1)实验中应沿竖直方向 拉动弹簧测力计。
(2)小组同学发现实验过程中边拉动测力计边读数时,弹簧测力计的示数不稳定,所以他认为应该在测力计静止时读数,你认为这样的想法 (选填“正确”或“不正确”),因为没有考虑到 对滑轮组机械效率的影响。
(3)用如图丁所示装置进行实验,得出表中第4次实验数据,请将表中的两个数据填写完整。
(4)通过比较 两次实验数据可得出结论:使用同一滑轮组提升同一重物时,滑轮组的机械效率与绳子绕法无关。
(5)通过比较 两次实验数据可得出结论:使用同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高。
(6)通过比较3、4两次实验数据可得出结论:
。
2 机械效率的定性比较
3.分别使用定滑轮、动滑轮、两个定滑轮和两个动滑轮组成的滑轮组,匀速提升同一物体到同一高度处,其机械效率分别为η定、η动、η组(不计绳重和摩擦,设每个滑轮质量相等),则下列选项中正确的是 ( )
A.η组<η动<η定 B.η动<η定<η组
C.η定<η动<η组 D.η定<η组<η动
4.(2020甘孜州)某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮等重),在相同时间内把重物G提升相同高度,F1和F2的大小相等,不计绳重及摩擦,下列说法正确的是 ( )
A.力F1和F2做功的功率相同
B.力F1和F2做的总功相同
C.乙滑轮组更省力,两个滑轮组机械效率一样大
D.甲滑轮组的机械效率比乙滑轮组的机械效率高
5.(2021自贡)如图所示,将规格完全相同的滑轮用绳子绕成图中的甲、乙滑轮组。使用甲、乙滑轮组分别匀速提升重力为G1、G2的两物体,升高相同的高度。绳自由端施加的拉力大小分别为F1和F2,物重G1>G2,不计绳重和摩擦。则下列判断正确的是 ( )
A.拉力F1一定大于F2
B.乙滑轮组的机械效率较高
C.甲、乙滑轮组的有用功相同
D.甲的额外功与有用功的比值较小
3 测量斜面的机械效率
6.(2020河北)斜面是一种简单机械,在生活和生产中使用斜面的好处是可以省力,如: 。那么斜面的省力情况与哪些因素有关呢 (使用斜面的省力情况可以通过比较沿斜面的拉力F与物体的重力G的比值大小来判定,比值越小,越省力)
小明提出了如下猜想:
猜想1:与斜面的表面材料有关;
猜想2:与斜面的倾斜程度有关;
猜想3:与物体受到的重力大小有关。
实验序号 1 2 3 4 5 6
斜面倾角 θ θ θ θ θ1(θ1>θ) θ2(θ2>θ1)
斜面的表 面材料 木板 毛巾 木板 木板 木板 木板
物块重 G/N 2.0 2.0 4.0 6.0 2.0 2.0
沿斜面拉 力F/N 1.35 1.52 2.70 4.05 1.52 1.70
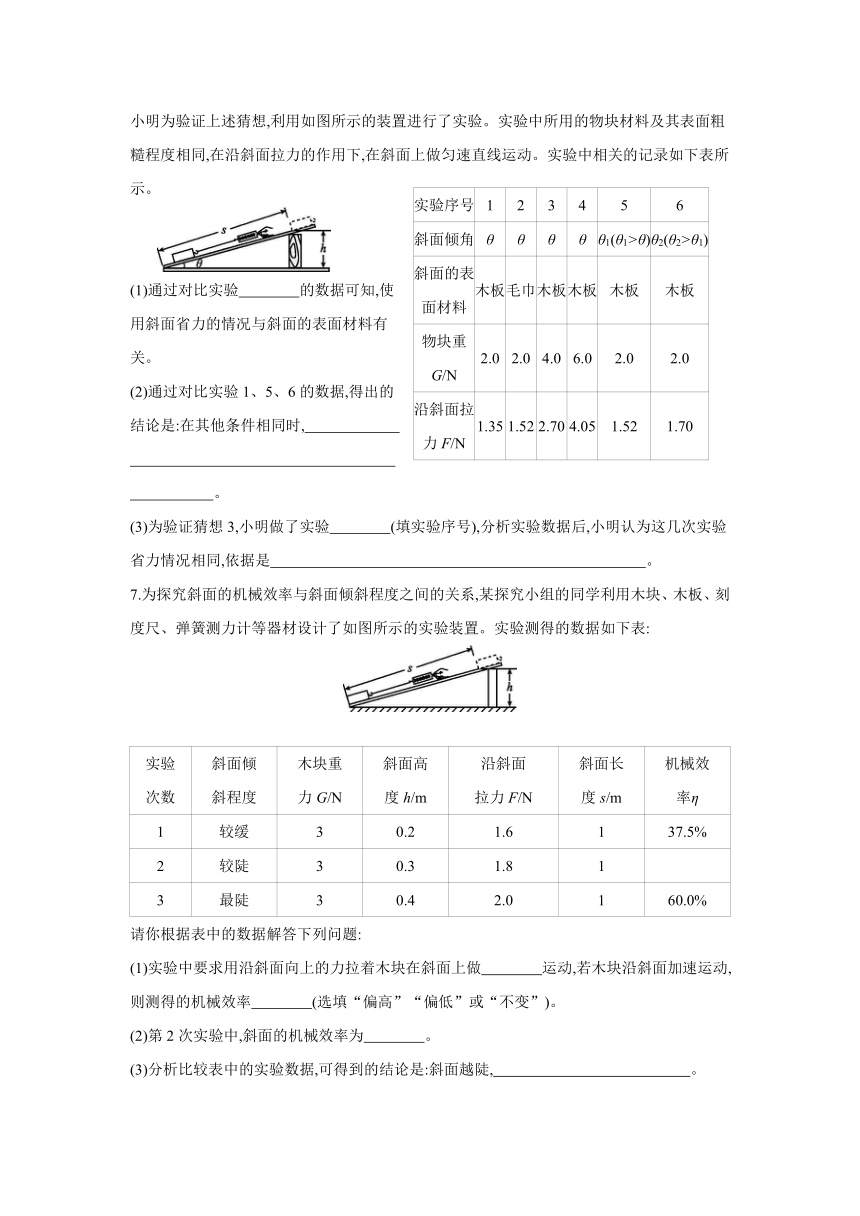
小明为验证上述猜想,利用如图所示的装置进行了实验。实验中所用的物块材料及其表面粗糙程度相同,在沿斜面拉力的作用下,在斜面上做匀速直线运动。实验中相关的记录如下表所示。
(1)通过对比实验 的数据可知,使用斜面省力的情况与斜面的表面材料有关。
(2)通过对比实验1、5、6的数据,得出的结论是:在其他条件相同时,
。
(3)为验证猜想3,小明做了实验 (填实验序号),分析实验数据后,小明认为这几次实验省力情况相同,依据是 。
7.为探究斜面的机械效率与斜面倾斜程度之间的关系,某探究小组的同学利用木块、木板、刻度尺、弹簧测力计等器材设计了如图所示的实验装置。实验测得的数据如下表:
实验 次数 斜面倾 斜程度 木块重 力G/N 斜面高 度h/m 沿斜面 拉力F/N 斜面长 度s/m 机械效 率η
1 较缓 3 0.2 1.6 1 37.5%
2 较陡 3 0.3 1.8 1
3 最陡 3 0.4 2.0 1 60.0%
请你根据表中的数据解答下列问题:
(1)实验中要求用沿斜面向上的力拉着木块在斜面上做 运动,若木块沿斜面加速运动,则测得的机械效率 (选填“偏高”“偏低”或“不变”)。
(2)第2次实验中,斜面的机械效率为 。
(3)分析比较表中的实验数据,可得到的结论是:斜面越陡, 。
(4)除了倾斜程度会影响斜面的机械效率,你还能猜想到斜面的 也会影响到斜面的机械效率,这样猜想的依据是 。
(5)当斜面长度一定时,斜面的机械效率η与斜面的高度h之间的关系大概如图中 所示。
4 测量杠杆的机械效率
8.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速缓慢地拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)图中弹簧测力计的示数F为 N,钩码总重G为1.0 N,钩码上升高度h为0.1 m,测力计移动的距离s为0.3 m,则杠杆的机械效率为 %。请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一名同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总 重G/N 钩码移 动距离 h/m 拉力 F/N 测力计 移动距 离s/m 机械效 率η
1 A点 1.5 0.10 0.7 0.30 71.4%
2 B点 2.0 0.15 1.2 0.30 83.3%
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重力有关,钩码越重,机械效率越高”的结论 答: 。
请简要说明两个理由:
① ;
② 。
第3节 机械效率
第2课时 机械效率的测量
1.匀速缓慢 (1)5.0 2 75% (2)变小
拉动弹簧测力计时,应沿竖直向上的方向匀速缓慢拉动绳子自由端。(1)物体上升的高度是5.0 cm;弹簧测力计的示数为2 N;该滑轮组的机械效率为η=====0.75=75%。(2)当被提升物重不变时,增加一个动滑轮,相当于在有用功不变的情况下增大了额外功,此时的机械效率会减小。
2.(1)匀速缓慢 (2)不正确 摩擦
(3)0.4 80% (4)1、2 (5)2、3
(6)使用不同滑轮组提升相同重物时,动滑轮越轻,滑轮组的机械效率越高(或使用不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率越低)
(1)实验中应沿竖直方向匀速缓慢拉动弹簧测力计。(2)在弹簧测力计静止时读数,由于轮与轴、绳与轮之间有摩擦,所以测力计示数偏小,这样的想法是不正确的。(3)图丁中,承担总重的绳子段数n=4,绳端移动距离s=nh=4×0.1 m=0.4 m,滑轮组的机械效率:η====0.8=80%。
3.A 匀速提升同一物体到同一高度处,由W有=Gh可知,三种情况下做的有用功相同;不计绳重和摩擦,所做的额外功:W额=G动h。使用定滑轮、动滑轮、滑轮组时,动滑轮的个数分别为0、1、2,则做的额外功:W额定4.D 由图知,甲滑轮组中承担物重的绳子段数为3,乙滑轮组中承担物重的绳子段数为4。若重物上升高度为h,则两滑轮组中绳端移动的距离分别为s甲=3h,s乙=4h;甲滑轮组中拉力做的总功为W甲总=F1×3h,乙滑轮组中拉力做的总功为W乙总=F2×4h,已知F1=F2,所以W甲总η乙,故C错误,D正确。
5.D 由图可知,甲、乙动滑轮上绳子的有效段数分别为3和2,且物重G1>G2,动滑轮重G动相同,由公式:F=(G+G动)可知:F1与F2的大小关系不能确定,故A错误;已知物体上升的高度h相同,且物重G1>G2,动滑轮重G动相同,由公式W有=Gh、W额=G动h可知,甲的有用功大于乙的有用功,两者的额外功相同,则甲的额外功与有用功的比值较小,故C错误、D正确;再由公式:η==可知:在额外功相同时,甲的有用功大,其效率就高,故B错误。
6.盘山公路 (1)1、2
(2)斜面的倾斜程度越小,提升物体越省力 (3)1、3、4 根据1、3、4的实验数据可知,物体的重力变为原来的几倍,拉力也变为原来的几倍,即沿斜面的拉力F与物体的重力G的比值大小相等
7.(1)匀速直线 偏低 (2)50%
(3)机械效率越高
(4)粗糙程度 斜面越粗糙,摩擦力越大,做的额外功越多,机械效率就越低 (5)C
8.(1)0.5 66.7
使用杠杆时需要克服杠杆自重(或克服摩擦力)做功
(2)不能 ①两次实验时钩码没有挂在同一位置
②仅根据一次对比实验所得的结论不可靠
(1)由图示可知,测力计的示数F为0.5 N。杠杆的机械效率为η===≈0.667=66.7%。使用该杠杆工作时,克服杠杆重力和摩擦力所做的功就是额外功。(2)第1次实验,钩码挂在A点,测出的机械效率为71.4%,第2次实验,钩码挂在B点,测出的机械效率为83.3%,因为钩码的悬挂点不同,并且只有一次对比数据,所以不能得出“杠杆的机械效率与所挂钩码的重力有关,钩码越重,机械效率越高”的结论。
第2课时 机械效率的测量
1 测量滑轮组的机械效率
1.图甲是某学习小组“测量滑轮组的机械效率”的示意图。用弹簧测力计竖直向上 拉动绳子自由端,将重为4.5 N的物体从A位置提升到A'位置,同时弹簧测力计从图中的B位置上升到B'位置,在这个过程中,弹簧测力计的示数如图乙所示。请你根据他们做的实验回答下列问题:
(1)物体被提升的高度是 cm,拉力是 N,该滑轮组的机械效率η= 。
(2)若在图甲装置的基础上,增加一个动滑轮,改为如图丙所示的装置,提升同一物体,则滑轮组的机械效率将 (选填“变大”“变小”或“不变”)。
2.某小组在“测量滑轮组的机械效率”的实验中得到的数据如下表所示,实验装置如图所示。
实验 次数 钩码重 G/N 钩码上升 高度h/m 绳端拉 力F/N 绳端移动 距离s/m 机械 效率η
1 4 0.1 2.7 0.2 74%
2 4 0.1 1.8 0.3 74%
3 8 0.1 3.1 0.3 86%
4 8 0.1 2.5
(1)实验中应沿竖直方向 拉动弹簧测力计。
(2)小组同学发现实验过程中边拉动测力计边读数时,弹簧测力计的示数不稳定,所以他认为应该在测力计静止时读数,你认为这样的想法 (选填“正确”或“不正确”),因为没有考虑到 对滑轮组机械效率的影响。
(3)用如图丁所示装置进行实验,得出表中第4次实验数据,请将表中的两个数据填写完整。
(4)通过比较 两次实验数据可得出结论:使用同一滑轮组提升同一重物时,滑轮组的机械效率与绳子绕法无关。
(5)通过比较 两次实验数据可得出结论:使用同一滑轮组提升重物时,物重越大,滑轮组的机械效率越高。
(6)通过比较3、4两次实验数据可得出结论:
。
2 机械效率的定性比较
3.分别使用定滑轮、动滑轮、两个定滑轮和两个动滑轮组成的滑轮组,匀速提升同一物体到同一高度处,其机械效率分别为η定、η动、η组(不计绳重和摩擦,设每个滑轮质量相等),则下列选项中正确的是 ( )
A.η组<η动<η定 B.η动<η定<η组
C.η定<η动<η组 D.η定<η组<η动
4.(2020甘孜州)某实验小组分别用如图所示的甲、乙两个滑轮组(每个滑轮等重),在相同时间内把重物G提升相同高度,F1和F2的大小相等,不计绳重及摩擦,下列说法正确的是 ( )
A.力F1和F2做功的功率相同
B.力F1和F2做的总功相同
C.乙滑轮组更省力,两个滑轮组机械效率一样大
D.甲滑轮组的机械效率比乙滑轮组的机械效率高
5.(2021自贡)如图所示,将规格完全相同的滑轮用绳子绕成图中的甲、乙滑轮组。使用甲、乙滑轮组分别匀速提升重力为G1、G2的两物体,升高相同的高度。绳自由端施加的拉力大小分别为F1和F2,物重G1>G2,不计绳重和摩擦。则下列判断正确的是 ( )
A.拉力F1一定大于F2
B.乙滑轮组的机械效率较高
C.甲、乙滑轮组的有用功相同
D.甲的额外功与有用功的比值较小
3 测量斜面的机械效率
6.(2020河北)斜面是一种简单机械,在生活和生产中使用斜面的好处是可以省力,如: 。那么斜面的省力情况与哪些因素有关呢 (使用斜面的省力情况可以通过比较沿斜面的拉力F与物体的重力G的比值大小来判定,比值越小,越省力)
小明提出了如下猜想:
猜想1:与斜面的表面材料有关;
猜想2:与斜面的倾斜程度有关;
猜想3:与物体受到的重力大小有关。
实验序号 1 2 3 4 5 6
斜面倾角 θ θ θ θ θ1(θ1>θ) θ2(θ2>θ1)
斜面的表 面材料 木板 毛巾 木板 木板 木板 木板
物块重 G/N 2.0 2.0 4.0 6.0 2.0 2.0
沿斜面拉 力F/N 1.35 1.52 2.70 4.05 1.52 1.70
小明为验证上述猜想,利用如图所示的装置进行了实验。实验中所用的物块材料及其表面粗糙程度相同,在沿斜面拉力的作用下,在斜面上做匀速直线运动。实验中相关的记录如下表所示。
(1)通过对比实验 的数据可知,使用斜面省力的情况与斜面的表面材料有关。
(2)通过对比实验1、5、6的数据,得出的结论是:在其他条件相同时,
。
(3)为验证猜想3,小明做了实验 (填实验序号),分析实验数据后,小明认为这几次实验省力情况相同,依据是 。
7.为探究斜面的机械效率与斜面倾斜程度之间的关系,某探究小组的同学利用木块、木板、刻度尺、弹簧测力计等器材设计了如图所示的实验装置。实验测得的数据如下表:
实验 次数 斜面倾 斜程度 木块重 力G/N 斜面高 度h/m 沿斜面 拉力F/N 斜面长 度s/m 机械效 率η
1 较缓 3 0.2 1.6 1 37.5%
2 较陡 3 0.3 1.8 1
3 最陡 3 0.4 2.0 1 60.0%
请你根据表中的数据解答下列问题:
(1)实验中要求用沿斜面向上的力拉着木块在斜面上做 运动,若木块沿斜面加速运动,则测得的机械效率 (选填“偏高”“偏低”或“不变”)。
(2)第2次实验中,斜面的机械效率为 。
(3)分析比较表中的实验数据,可得到的结论是:斜面越陡, 。
(4)除了倾斜程度会影响斜面的机械效率,你还能猜想到斜面的 也会影响到斜面的机械效率,这样猜想的依据是 。
(5)当斜面长度一定时,斜面的机械效率η与斜面的高度h之间的关系大概如图中 所示。
4 测量杠杆的机械效率
8.用如图所示的实验装置测量杠杆的机械效率。实验时,竖直向上匀速缓慢地拉动弹簧测力计,使挂在较长杠杆下面的钩码缓缓上升。
(1)图中弹簧测力计的示数F为 N,钩码总重G为1.0 N,钩码上升高度h为0.1 m,测力计移动的距离s为0.3 m,则杠杆的机械效率为 %。请写出使用该杠杆做额外功的一个原因: 。
(2)为了进一步研究杠杆的机械效率与哪些因素有关,一名同学用该实验装置,先后将钩码挂在A、B两点,测量并计算得到下表所示的两组数据:
次数 钩码 悬挂点 钩码总 重G/N 钩码移 动距离 h/m 拉力 F/N 测力计 移动距 离s/m 机械效 率η
1 A点 1.5 0.10 0.7 0.30 71.4%
2 B点 2.0 0.15 1.2 0.30 83.3%
根据表中数据,能否得出“杠杆的机械效率与所挂钩码的重力有关,钩码越重,机械效率越高”的结论 答: 。
请简要说明两个理由:
① ;
② 。
第3节 机械效率
第2课时 机械效率的测量
1.匀速缓慢 (1)5.0 2 75% (2)变小
拉动弹簧测力计时,应沿竖直向上的方向匀速缓慢拉动绳子自由端。(1)物体上升的高度是5.0 cm;弹簧测力计的示数为2 N;该滑轮组的机械效率为η=====0.75=75%。(2)当被提升物重不变时,增加一个动滑轮,相当于在有用功不变的情况下增大了额外功,此时的机械效率会减小。
2.(1)匀速缓慢 (2)不正确 摩擦
(3)0.4 80% (4)1、2 (5)2、3
(6)使用不同滑轮组提升相同重物时,动滑轮越轻,滑轮组的机械效率越高(或使用不同滑轮组提升相同重物时,动滑轮越重,滑轮组的机械效率越低)
(1)实验中应沿竖直方向匀速缓慢拉动弹簧测力计。(2)在弹簧测力计静止时读数,由于轮与轴、绳与轮之间有摩擦,所以测力计示数偏小,这样的想法是不正确的。(3)图丁中,承担总重的绳子段数n=4,绳端移动距离s=nh=4×0.1 m=0.4 m,滑轮组的机械效率:η====0.8=80%。
3.A 匀速提升同一物体到同一高度处,由W有=Gh可知,三种情况下做的有用功相同;不计绳重和摩擦,所做的额外功:W额=G动h。使用定滑轮、动滑轮、滑轮组时,动滑轮的个数分别为0、1、2,则做的额外功:W额定
5.D 由图可知,甲、乙动滑轮上绳子的有效段数分别为3和2,且物重G1>G2,动滑轮重G动相同,由公式:F=(G+G动)可知:F1与F2的大小关系不能确定,故A错误;已知物体上升的高度h相同,且物重G1>G2,动滑轮重G动相同,由公式W有=Gh、W额=G动h可知,甲的有用功大于乙的有用功,两者的额外功相同,则甲的额外功与有用功的比值较小,故C错误、D正确;再由公式:η==可知:在额外功相同时,甲的有用功大,其效率就高,故B错误。
6.盘山公路 (1)1、2
(2)斜面的倾斜程度越小,提升物体越省力 (3)1、3、4 根据1、3、4的实验数据可知,物体的重力变为原来的几倍,拉力也变为原来的几倍,即沿斜面的拉力F与物体的重力G的比值大小相等
7.(1)匀速直线 偏低 (2)50%
(3)机械效率越高
(4)粗糙程度 斜面越粗糙,摩擦力越大,做的额外功越多,机械效率就越低 (5)C
8.(1)0.5 66.7
使用杠杆时需要克服杠杆自重(或克服摩擦力)做功
(2)不能 ①两次实验时钩码没有挂在同一位置
②仅根据一次对比实验所得的结论不可靠
(1)由图示可知,测力计的示数F为0.5 N。杠杆的机械效率为η===≈0.667=66.7%。使用该杠杆工作时,克服杠杆重力和摩擦力所做的功就是额外功。(2)第1次实验,钩码挂在A点,测出的机械效率为71.4%,第2次实验,钩码挂在B点,测出的机械效率为83.3%,因为钩码的悬挂点不同,并且只有一次对比数据,所以不能得出“杠杆的机械效率与所挂钩码的重力有关,钩码越重,机械效率越高”的结论。
