2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2.4组合数课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 15:03:08 | ||
图片预览





文档简介
(共18张PPT)
6.2.4 组合数
1.组合的定义
2.判断一个计数问题是排列问题还是组合问题的方法:
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
复习引入
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,并用符号 表示.
“一个组合”是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数”是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,它是一个非零自然数.
探究新知
组合数的定义和表示:
例如,从3个不同元素中取出2个元素的组合数,表示为 ,
从4个不同元素中取出3个元素的组合数,表示为 .
组合与组合数的区别:
探究新知
前面已经提到,组合与排列有关系,我们能否利用这种关系,由排列数 来求组合数 呢?
?
探究
回顾:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
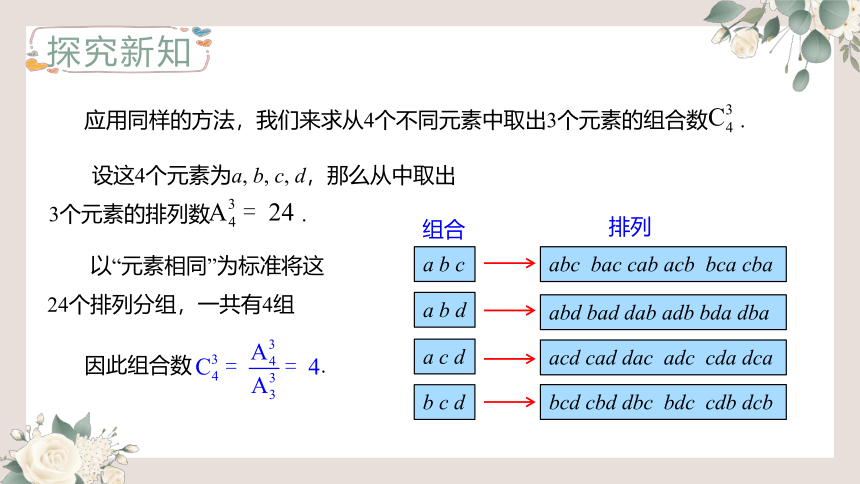
应用同样的方法,我们来求从4个不同元素中取出3个元素的组合数 .
组合
a b c
a b d
a c d
b c d
排列
abc bac cab acb bca cba
abd bad dab adb bda dba
acd cad dac adc cda dca
bcd cbd dbc bdc cdb dcb
探究新知
设这4个元素为a, b, c, d,那么从中取出3个元素的排列数 .
因此组合数 .
以“元素相同”为标准将这24个排列分组,一共有4组
探究新知
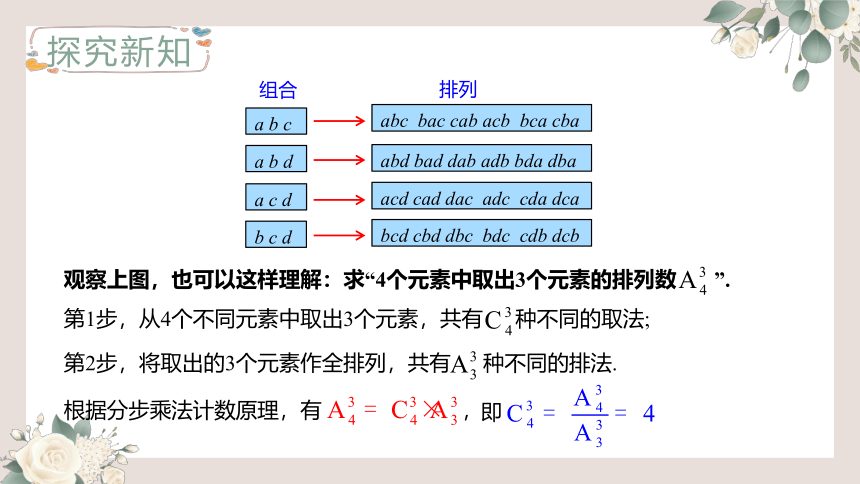
观察上图,也可以这样理解:求“4个元素中取出3个元素的排列数 ”.
第1步,从4个不同元素中取出3个元素,共有 种不同的取法;
第2步,将取出的3个元素作全排列,共有 种不同的排法.
根据分步乘法计数原理,有 ,
即
组合
a b c
a b d
a c d
b c d
排列
abc bac cab acb bca cba
abd bad dab adb bda dba
acd cad dac adc cda dca
bcd cbd dbc bdc cdb dcb
同样地,求“从n个不同元素中取出m个元素的排列数 ”,可以看作由以下两个步骤得到:
第1步,从n个不同元素中取出m个元素,共有 种不同的取法;
第2步,将取出的m个元素作全排列,共有 种不同的排法.
根据分步乘法计数原理,有
因此,
探究新知
因为 ,所以上面的组合数公式还可以写成
这里n,m∈N* ,并且m≤n. 这个公式叫做组合数公式.
规定
例1 计算: (1) ; (2) ; (3) ; (4) .
解:
典例分析
追问: 分别观察例中(1)与(2), (3)与(4)的结果,你有什么发现和猜想?
证明:
直观解释:
该性质反映了组合数的对称性. 其组合意义是从n个不同的元素中任取m个元素的组合与任取(n-m)个元素的组合是一一对应(一种取法对应一种剩法).
因为从n个不同元素中取出m个元素后,就剩下(n-m)个元素,因此从n个不同元素中取出m个元素的方法,与从n个不同元素中取出(n-m)个元素的方法是一一对应的,因此取法是一样多的,就是说从n个不同元素中取出m个元素的每一个组合,都对应着从n个不同元素中取出(n-m)个元素的唯一的一个组合,反过来也一样. 即从n个不同元素中取出m个元素的组合数 等于从n个不同元素中取出(n-m)个元素的组合数 ,也就是 .
探究新知
证明:
直观解释:
该性质也可以根据组合数的定义与分类加法计数原理直接得出,在确定从(n+1)个不同元素中取m个元素的方法时,对于某一元素,只存在着取与不取两种可能.
如果取这一元素,则需从剩下的n个元素中再取出(m-1)个元素,所以共有 种取法;如果不取这一元素,则需从剩下的n个元素中再取出m个元素,所以共有 种取法. 由分类加法计数原理,得 .
探究新知
小试牛刀
1.计算:
解:
(1)每个小组有多少种选法
(2)如果还要从选出的同学中指定1名作替补,那么每小组有多少种选法
(3)如果还要将选出的同学分别指定为第一、二、三、四辩手,那么每小组有多少种选法
例2 班上每个小组有12名同学,现要从每个小组选4名同学代表本组与其他小组进行辩论赛.
典例分析
解答组合问题的关键是用好组合的定义和两个基本原理, 只选不排,合理分类、分步.
1.一位教练的足球队共有17名初级学员, 他们中以前没有一人参加过比赛, 按照足球比赛规则, 比赛时一个足球队的上场队员是11人. 问:
(1)这位教练从这17名学员中可以形成多少种学员上场方案
(2)如果在选出11名上场队员时, 还要确定其中的守门员, 那么教练员有多少种方式做这件事情
巩固练习
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,
所以抽法种数为
典例分析
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
例3 在100件产品中,有98件合格品,2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
例3 在100件产品中,有98件合格品,2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
典例分析
方法2: 抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
解:(3)方法1:从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
“至少”“至多”的问题,通常用分类法或间接法求解
变式:把(3)中的“至少”改为“至多”, 则抽法有多少种
(4)如果物理和化学都没被选,那么共有多少种不同的选法
(5)如果物理、化学和生物至少有2门被选,那么共有多少种不同的选法
1.有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门考试成绩.
(1)一共有多少种不同的选法
(2)如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3)如果物理和化学至少有1门被选,那么共有多少种不同的选法
巩固练习
2.按下列条件, 从12人中选出5人, 有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;
课堂练习
课堂小结
1.组合数的定义和表示
把从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,并用符号 表示.
2.组合数的公式
3.组合数的性质
6.2.4 组合数
1.组合的定义
2.判断一个计数问题是排列问题还是组合问题的方法:
排列问题
组合问题
若交换某两个元素的位置对结果有影响,则是排列问题,即排列问题与选取的顺序有关.
若交换任意两个元素的位置对结果没有影响,则是组合问题,即组合问题与选取的顺序无关.
一般地,从n个不同元素中取出m(m≤n)个元素作为一组,叫做从n个不同元素中取出m个元素的一个组合(combination).
复习引入
从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,并用符号 表示.
“一个组合”是指“从n个不同元素中取出m(m≤n)个元素合成一组”,它不是一个数;
“组合数”是指“从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数”,它是一个非零自然数.
探究新知
组合数的定义和表示:
例如,从3个不同元素中取出2个元素的组合数,表示为 ,
从4个不同元素中取出3个元素的组合数,表示为 .
组合与组合数的区别:
探究新知
前面已经提到,组合与排列有关系,我们能否利用这种关系,由排列数 来求组合数 呢?
?
探究
回顾:从甲、乙、丙3名同学中选出2名参加一项活动,有多少种不同的选法?
组合
甲乙
甲丙
乙丙
甲乙,乙甲
甲丙,丙甲
乙丙,丙乙
排列
应用同样的方法,我们来求从4个不同元素中取出3个元素的组合数 .
组合
a b c
a b d
a c d
b c d
排列
abc bac cab acb bca cba
abd bad dab adb bda dba
acd cad dac adc cda dca
bcd cbd dbc bdc cdb dcb
探究新知
设这4个元素为a, b, c, d,那么从中取出3个元素的排列数 .
因此组合数 .
以“元素相同”为标准将这24个排列分组,一共有4组
探究新知
观察上图,也可以这样理解:求“4个元素中取出3个元素的排列数 ”.
第1步,从4个不同元素中取出3个元素,共有 种不同的取法;
第2步,将取出的3个元素作全排列,共有 种不同的排法.
根据分步乘法计数原理,有 ,
即
组合
a b c
a b d
a c d
b c d
排列
abc bac cab acb bca cba
abd bad dab adb bda dba
acd cad dac adc cda dca
bcd cbd dbc bdc cdb dcb
同样地,求“从n个不同元素中取出m个元素的排列数 ”,可以看作由以下两个步骤得到:
第1步,从n个不同元素中取出m个元素,共有 种不同的取法;
第2步,将取出的m个元素作全排列,共有 种不同的排法.
根据分步乘法计数原理,有
因此,
探究新知
因为 ,所以上面的组合数公式还可以写成
这里n,m∈N* ,并且m≤n. 这个公式叫做组合数公式.
规定
例1 计算: (1) ; (2) ; (3) ; (4) .
解:
典例分析
追问: 分别观察例中(1)与(2), (3)与(4)的结果,你有什么发现和猜想?
证明:
直观解释:
该性质反映了组合数的对称性. 其组合意义是从n个不同的元素中任取m个元素的组合与任取(n-m)个元素的组合是一一对应(一种取法对应一种剩法).
因为从n个不同元素中取出m个元素后,就剩下(n-m)个元素,因此从n个不同元素中取出m个元素的方法,与从n个不同元素中取出(n-m)个元素的方法是一一对应的,因此取法是一样多的,就是说从n个不同元素中取出m个元素的每一个组合,都对应着从n个不同元素中取出(n-m)个元素的唯一的一个组合,反过来也一样. 即从n个不同元素中取出m个元素的组合数 等于从n个不同元素中取出(n-m)个元素的组合数 ,也就是 .
探究新知
证明:
直观解释:
该性质也可以根据组合数的定义与分类加法计数原理直接得出,在确定从(n+1)个不同元素中取m个元素的方法时,对于某一元素,只存在着取与不取两种可能.
如果取这一元素,则需从剩下的n个元素中再取出(m-1)个元素,所以共有 种取法;如果不取这一元素,则需从剩下的n个元素中再取出m个元素,所以共有 种取法. 由分类加法计数原理,得 .
探究新知
小试牛刀
1.计算:
解:
(1)每个小组有多少种选法
(2)如果还要从选出的同学中指定1名作替补,那么每小组有多少种选法
(3)如果还要将选出的同学分别指定为第一、二、三、四辩手,那么每小组有多少种选法
例2 班上每个小组有12名同学,现要从每个小组选4名同学代表本组与其他小组进行辩论赛.
典例分析
解答组合问题的关键是用好组合的定义和两个基本原理, 只选不排,合理分类、分步.
1.一位教练的足球队共有17名初级学员, 他们中以前没有一人参加过比赛, 按照足球比赛规则, 比赛时一个足球队的上场队员是11人. 问:
(1)这位教练从这17名学员中可以形成多少种学员上场方案
(2)如果在选出11名上场队员时, 还要确定其中的守门员, 那么教练员有多少种方式做这件事情
巩固练习
解:(1)所有的不同抽法种数,就是从100件产品中抽出3件的组合数,
所以抽法种数为
典例分析
(2) 从2件次品中抽出1件的抽法有 种,从98件合格品中抽出2件的抽法有 种,因此抽出的3件中恰好有1件次品的抽法种数为
例3 在100件产品中,有98件合格品,2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
例3 在100件产品中,有98件合格品,2件次品. 从这100件产品中任意抽出3件.
(1)有多少种不同的抽法?
(2)抽出的3件中恰好有1件是次品的抽法有多少种?
(3)抽出的3件中至少有1件是次品的抽法有多少种?
典例分析
方法2: 抽出的3件中至少有1件是次品的抽法种数,就是从100件产品中抽出3件的抽法种数减去3件都是合格品的抽法种数,即
解:(3)方法1:从100件产品抽出的3件中至少有1件是次品,包括有1件次品和有2件次品两种情况,因此根据分类加法计数原理,抽出的3件中至少有1件是次品的抽法种数为
“至少”“至多”的问题,通常用分类法或间接法求解
变式:把(3)中的“至少”改为“至多”, 则抽法有多少种
(4)如果物理和化学都没被选,那么共有多少种不同的选法
(5)如果物理、化学和生物至少有2门被选,那么共有多少种不同的选法
1.有政治、历史、地理、物理、化学、生物这6门学科的学业水平考试成绩,现要从中选3门考试成绩.
(1)一共有多少种不同的选法
(2)如果物理和化学恰有1门被选,那么共有多少种不同的选法
(3)如果物理和化学至少有1门被选,那么共有多少种不同的选法
巩固练习
2.按下列条件, 从12人中选出5人, 有多少种不同选法?
(1)甲、乙、丙三人必须当选;
(2)甲、乙、丙三人不能当选;
(3)甲必须当选,乙、丙不能当选;
(4)甲、乙、丙三人只有一人当选;
(5)甲、乙、丙三人至多2人当选;
(6)甲、乙、丙三人至少1人当选;
课堂练习
课堂小结
1.组合数的定义和表示
把从n个不同元素中取出m(m≤n)个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,并用符号 表示.
2.组合数的公式
3.组合数的性质
