2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合之综合应用课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.2排列组合之综合应用课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
6.2 排列组合的综合应用
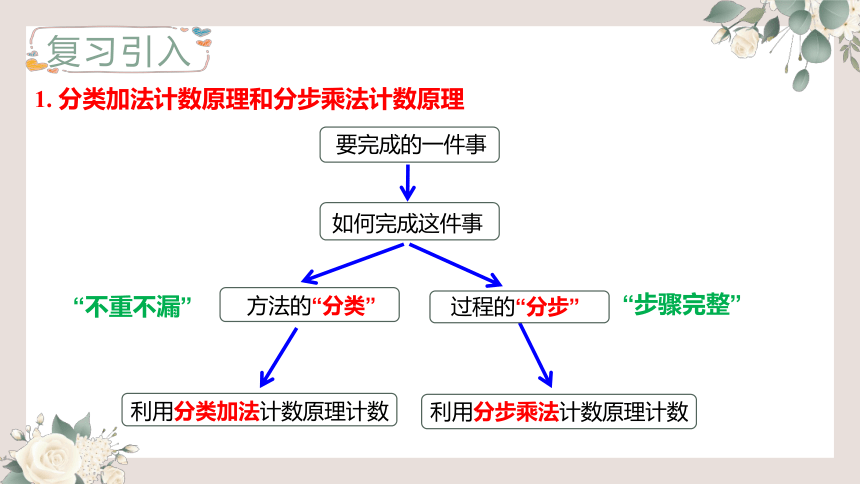
1. 分类加法计数原理和分步乘法计数原理
要完成的一件事
如何完成这件事
方法的“分类”
利用分类加法计数原理计数
利用分步乘法计数原理计数
过程的“分步”
“不重不漏”
“步骤完整”
复习引入
2.排列数、组合数的公式及性质
类型 排列数 组合数
公式
性质
备注 n,m∈N* 且m≤n
题型一:排列问题
例1 有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排,多少种不同的排法?
(2)全体排成一排,甲不站排头也不站排尾,多少种不同的排法?
(3)若三个女生要站在一起,有多少种不同的排法?
(4)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
(5)若三个女生互不相邻,有多少种不同的排法?
(6)男生、女生相间排列,有多少种不同的排法?
(7) 全体排成一排,甲必须排在乙前面,有多少种不同的排法?
(8) 全体排成一排,甲、乙、丙的先后顺序不可以改变,有多少种不同的排法?
典例分析
(1)选5人排成一排,多少种不同的排法?
(2)全体排成一排,甲不站排头也不站排尾,多少种不同的排法?
典例分析
解: (1)从7人中选5人排列,有
(2)(特殊元素优先法)先排甲,有5种方法,其余6人有 种排列方法,共有
(特殊位置优先法)首尾位置可安排另6人中的两人,有 种排法,其他有 种排法,共有
对于有限制条件的排列问题, 常常使用“直接法”(主要为“特殊位置法”和“特殊元素法”)或者“间接法”, 即优先考虑限制条件.
“定位”问题,优先法
捆绑法
解: (3)将三个女孩看作一人与四个男孩排队,有 种排法,而三个女孩之间有 种排法,所以不同的排法共有: 种.
(3)若三个女生要站在一起,有多少种不同的排法?
典例分析
(4)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
解:(4)将三个女孩看作一人,将四个男孩也看作一人,有 种排法,而三个女孩之间有 种排法,四个男孩之间有 种排法,共有: 种.
对于相邻问题, 常常先将要相邻的元素捆绑在一起, 视作为一个元素, 与其余元素全排列, 再松绑后它们之间进行全排列.
“相邻”问题,捆绑法
典例分析
(5)若三个女生互不相邻,有多少种不同的排法?
解: (5)先把四个男孩排成一排有 种排法,在每一排列中有五个空位(包括两端),再把三个女孩插入空位中有 种方法,所以共有: (种)排法.
插空法
典例分析
(6)男生、女生相间排列,有多少种不同的排法?
解:(6)先把四个男孩排成一排有 种排法,在每一排列中有三个空位(不包括两端),再把三个女孩插入空位中有 种方法,共有: (种).
插空法
对于不相邻问题, 先将其余元素全排列, 再将这些不相邻的元素插入空位中, 这种方法就是插空法.
“相隔”问题,插空法
典例分析
(7) 全体排成一排,甲必须排在乙前面,有多少种不同的排法?
(8) 全体排成一排,甲、乙、丙的先后顺序不可以改变,有多少种不同的排法?
解:(7)先不考虑顺序,将全体进行全排列,有 种排法,而甲、乙两人的全排列有 种方法,共有: (种).
典例分析
(8)先不考虑顺序,将全体进行全排列,有 种排法,而甲、乙、丙三人的全排列有 种方法,共有: (种).
“定序”问题,除序法
对于定序问题,可先不考虑顺序限制,全排列后,再除以定序元素的全排列.
直接法
优先法
捆绑法
插空法
定序问题除法处理
间接法
求解排列问题的6种主要方法
方法归纳
把符合条件的排列数直接列式计算
优先安排特殊元素或特殊位置
把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
对于定序问题,可先不考虑顺序限制,全排列后,再除以定序元素的全排列
正难则反、等价转化的方法
题型二:组合问题
例2 某市工商局对35种商品进行抽样检查,已知其中有15种假货. 现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
典例分析
解: (1)从余下的34种商品中选取2种,有 (种)取法.
(2)从余下的34种商品中选取3种,有 (种)取法.
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
典例分析
解:(3)从20种真货中选取1种,从15种真货中选取2种,
有 (种)取法.
(4)选取2种假货有 种,选取3种假货有 种,共有 种取法.
(5)选取3种商品的取法为 ,“选取3种假货”有 种取法,至多有2种假货在内的取法有 种.
组合问题的2类题型及求解方法
1.“含有”或“不含有”某些元素的组合题型:
(1)“含”,则先将这些元素取出,再由另外的元素补足;
(2)“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
2.“至少”或“至多”含有几个元素的组合题型:
解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.
用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
方法归纳
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(1)分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
(4) 分为三份,一份一本,一份两本,一份三本;
(5) 分为三份,每份两本;
(6) 分为三份,一份四本,一份一本,一份一本;
(7) 分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8) 分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9) 分给甲、乙、丙三人,每人至少一本.
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(1)分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(4) 分为三份,一份一本,一份两本,一份三本;
(5) 分为三份,每份两本;
(6) 分为三份,一份四本,一份一本,一份一本;
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(7) 分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8) 分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9) 分给甲、乙、丙三人,每人至少一本.
典例分析
1.完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法 计数原理解题.
2.部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.需要除以相同的组的“全排列”,保证没有重复.
3.非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象.
解题思想:先分组、后分配
分组分配问题
方法归纳
课堂小结
1.求解排列问题的6种主要方法
①直接法;②优先法;③捆绑法;
④插空法;⑤除序法;⑥间接法
2.组合问题的2类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型;
(2)“至少”或“至多”含有几个元素的组合题型.
3.分组分配问题
(1)完全平均分组:①只分组无分配;②分组且分配;
(2)部分平均分组;
(3)非平均分组.
6.2 排列组合的综合应用
1. 分类加法计数原理和分步乘法计数原理
要完成的一件事
如何完成这件事
方法的“分类”
利用分类加法计数原理计数
利用分步乘法计数原理计数
过程的“分步”
“不重不漏”
“步骤完整”
复习引入
2.排列数、组合数的公式及性质
类型 排列数 组合数
公式
性质
备注 n,m∈N* 且m≤n
题型一:排列问题
例1 有3名女生、4名男生,在下列不同条件下,求不同的排列方法总数.
(1)选5人排成一排,多少种不同的排法?
(2)全体排成一排,甲不站排头也不站排尾,多少种不同的排法?
(3)若三个女生要站在一起,有多少种不同的排法?
(4)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
(5)若三个女生互不相邻,有多少种不同的排法?
(6)男生、女生相间排列,有多少种不同的排法?
(7) 全体排成一排,甲必须排在乙前面,有多少种不同的排法?
(8) 全体排成一排,甲、乙、丙的先后顺序不可以改变,有多少种不同的排法?
典例分析
(1)选5人排成一排,多少种不同的排法?
(2)全体排成一排,甲不站排头也不站排尾,多少种不同的排法?
典例分析
解: (1)从7人中选5人排列,有
(2)(特殊元素优先法)先排甲,有5种方法,其余6人有 种排列方法,共有
(特殊位置优先法)首尾位置可安排另6人中的两人,有 种排法,其他有 种排法,共有
对于有限制条件的排列问题, 常常使用“直接法”(主要为“特殊位置法”和“特殊元素法”)或者“间接法”, 即优先考虑限制条件.
“定位”问题,优先法
捆绑法
解: (3)将三个女孩看作一人与四个男孩排队,有 种排法,而三个女孩之间有 种排法,所以不同的排法共有: 种.
(3)若三个女生要站在一起,有多少种不同的排法?
典例分析
(4)若三个女生要站在一起,四个男生也要站在一起,有多少种不同的排法?
解:(4)将三个女孩看作一人,将四个男孩也看作一人,有 种排法,而三个女孩之间有 种排法,四个男孩之间有 种排法,共有: 种.
对于相邻问题, 常常先将要相邻的元素捆绑在一起, 视作为一个元素, 与其余元素全排列, 再松绑后它们之间进行全排列.
“相邻”问题,捆绑法
典例分析
(5)若三个女生互不相邻,有多少种不同的排法?
解: (5)先把四个男孩排成一排有 种排法,在每一排列中有五个空位(包括两端),再把三个女孩插入空位中有 种方法,所以共有: (种)排法.
插空法
典例分析
(6)男生、女生相间排列,有多少种不同的排法?
解:(6)先把四个男孩排成一排有 种排法,在每一排列中有三个空位(不包括两端),再把三个女孩插入空位中有 种方法,共有: (种).
插空法
对于不相邻问题, 先将其余元素全排列, 再将这些不相邻的元素插入空位中, 这种方法就是插空法.
“相隔”问题,插空法
典例分析
(7) 全体排成一排,甲必须排在乙前面,有多少种不同的排法?
(8) 全体排成一排,甲、乙、丙的先后顺序不可以改变,有多少种不同的排法?
解:(7)先不考虑顺序,将全体进行全排列,有 种排法,而甲、乙两人的全排列有 种方法,共有: (种).
典例分析
(8)先不考虑顺序,将全体进行全排列,有 种排法,而甲、乙、丙三人的全排列有 种方法,共有: (种).
“定序”问题,除序法
对于定序问题,可先不考虑顺序限制,全排列后,再除以定序元素的全排列.
直接法
优先法
捆绑法
插空法
定序问题除法处理
间接法
求解排列问题的6种主要方法
方法归纳
把符合条件的排列数直接列式计算
优先安排特殊元素或特殊位置
把相邻元素看作一个整体与其他元素一起排列,同时注意捆绑元素的内部排列
对不相邻问题,先考虑不受限制的元素的排列,再将不相邻的元素插在前面元素排列的空当中
对于定序问题,可先不考虑顺序限制,全排列后,再除以定序元素的全排列
正难则反、等价转化的方法
题型二:组合问题
例2 某市工商局对35种商品进行抽样检查,已知其中有15种假货. 现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同取法有多少种?
(2)其中某一种假货不能在内,不同取法有多少种?
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
典例分析
解: (1)从余下的34种商品中选取2种,有 (种)取法.
(2)从余下的34种商品中选取3种,有 (种)取法.
(3)恰有2种假货在内,不同取法有多少种?
(4)至少有2种假货在内,不同取法有多少种?
(5)至多有2种假货在内,不同取法有多少种?
典例分析
解:(3)从20种真货中选取1种,从15种真货中选取2种,
有 (种)取法.
(4)选取2种假货有 种,选取3种假货有 种,共有 种取法.
(5)选取3种商品的取法为 ,“选取3种假货”有 种取法,至多有2种假货在内的取法有 种.
组合问题的2类题型及求解方法
1.“含有”或“不含有”某些元素的组合题型:
(1)“含”,则先将这些元素取出,再由另外的元素补足;
(2)“不含”,则先将这些元素剔除,再从剩下的元素中去选取.
2.“至少”或“至多”含有几个元素的组合题型:
解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解.
用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.
方法归纳
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(1)分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
(4) 分为三份,一份一本,一份两本,一份三本;
(5) 分为三份,每份两本;
(6) 分为三份,一份四本,一份一本,一份一本;
(7) 分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8) 分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9) 分给甲、乙、丙三人,每人至少一本.
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(1)分给甲、乙、丙三人,甲得一本,乙得两本,丙得三本;
(2) 分给甲、乙、丙三人,每人两本;
(3) 分给甲、乙、丙三人,甲得四本,乙得一本,丙得一本;
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(4) 分为三份,一份一本,一份两本,一份三本;
(5) 分为三份,每份两本;
(6) 分为三份,一份四本,一份一本,一份一本;
典例分析
题型三:分组分配问题
例3 六本不同的书,按下列要求各有多少种不同的分法?
(7) 分给甲、乙、丙三人,一人一本,一人两本,一人三本;
(8) 分给甲、乙、丙三人,一人得四本,另外两个人每个人得一本;
(9) 分给甲、乙、丙三人,每人至少一本.
典例分析
1.完全平均分组:在分组时,每组元素的个数都相等.
①只分组无分配时,需要除以这几组的“全排列”,以确保消去重复;
②分组且分配时,一种方法是先分组再分配;另一种方法是可以用分步乘法 计数原理解题.
2.部分平均分组:在分组时,每组的个数是不均等的,而是有一部分个数相同.需要除以相同的组的“全排列”,保证没有重复.
3.非平均分组:每组所要分的元素个数是不相同的.这种分组不考虑重复现象.
解题思想:先分组、后分配
分组分配问题
方法归纳
课堂小结
1.求解排列问题的6种主要方法
①直接法;②优先法;③捆绑法;
④插空法;⑤除序法;⑥间接法
2.组合问题的2类题型及求解方法
(1)“含有”或“不含有”某些元素的组合题型;
(2)“至少”或“至多”含有几个元素的组合题型.
3.分组分配问题
(1)完全平均分组:①只分组无分配;②分组且分配;
(2)部分平均分组;
(3)非平均分组.
