2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.1二项式定理课件 (共15张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册6.3.1二项式定理课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
6.3.1 二项式定理
创设情境
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
杨辉是中国南宋末年数学家、 教育家。“杨辉三角”出现 在杨辉编著的《详解九章算 法》一书中,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪. 在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角. 杨辉三角的发现要比欧洲早500年左右.
探究新知
杨辉三角的这七行数字表达的是什么内容,其内涵是什么?
?
探究
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
此表是一张二项式系数表,第一行数字对应(a+b)0展开式,第二行数字对应(a+b)1展开式,那么第n行数字对应什么?
(a+b)0
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
(a+b)1
探究新知
在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
?
探究
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
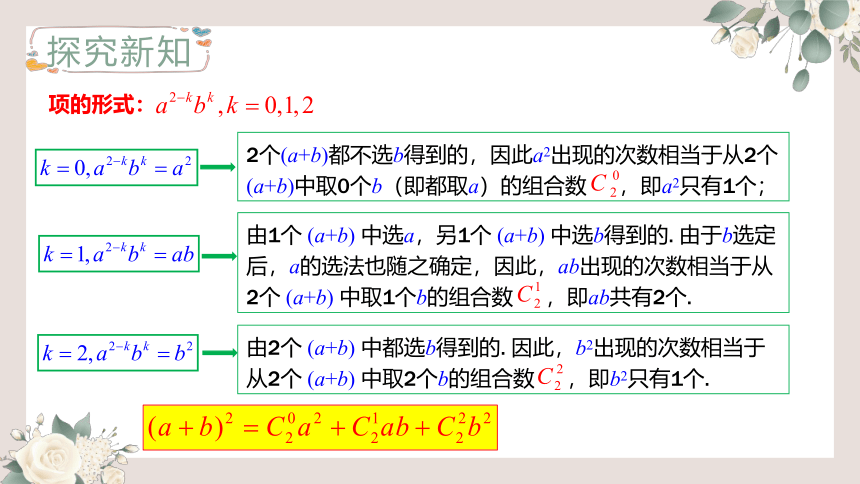
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
探究新知
探究新知
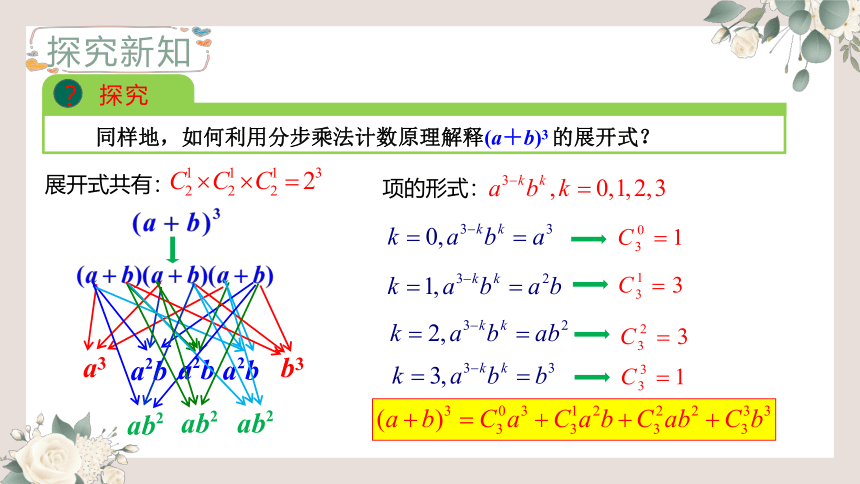
同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
?
探究
a3
a2b
a2b
a2b
b3
ab2
ab2
ab2
展开式共有:
项的形式:
a4
a3b
ab3
b4
a2b2
探究新知
根据你发现的规律,你能写出(a+b)4 的展开式吗?
?
探究
解:
(项的结构)
探究新知
进一步地,你能写出(a+b)n 的展开式吗?
?
探究
(项的系数)
概念形成
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
在二项式定理中,若设a=1, b=x,则得到公式
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
例1
求 的展开式.
解:
典例分析
求 的展开式.
变式1:
解:
典例分析
例1 (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例3
典例分析
解:
1.求 (2a+3b)6 的展开式的第3项.
巩固练习
2.求 的展开式的第r+1项.
解:
3.在 (x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是 .
-15
1.二项式定理
2.二项展开式的通项
3.二项式系数:
课堂小结
6.3.1 二项式定理
创设情境
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
杨辉是中国南宋末年数学家、 教育家。“杨辉三角”出现 在杨辉编著的《详解九章算 法》一书中,且我国北宋数学家贾宪(约公元11世纪)已经用过它,这表明我国发现这个表不晚于11世纪. 在欧洲,这个表被认为是法国数学家物理学家帕斯卡首先发现的,他们把这个表叫做帕斯卡三角. 杨辉三角的发现要比欧洲早500年左右.
探究新知
杨辉三角的这七行数字表达的是什么内容,其内涵是什么?
?
探究
一
一 一
一 二 一
一 三 三 一
一 四 六 四 一
一 五 十 十 五 一
一 六 十五 二十 十五 六 一
此表是一张二项式系数表,第一行数字对应(a+b)0展开式,第二行数字对应(a+b)1展开式,那么第n行数字对应什么?
(a+b)0
(a+b)2
(a+b)3
(a+b)4
(a+b)5
(a+b)6
(a+b)1
探究新知
在初中,我们用多项式乘法法则得到了(a+b)2 的展开式,如何利用分步乘法计数原理解释上述展开过程?
?
探究
(a+b)2=(a+b)(a+b)
=a×a+a×b+b×a+b×b
=a2+2ab+b2
从上述过程可以看到,(a+b)2是2个(a+b)相乘,根据多项式乘法法则,每个(a+b)在相乘时有两种选择,选a或选b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
于是,由分步乘法计数原理,在合并同类项之前,(a+b)2的展开式共有2×2=22项,而且每一项都是a2-k×bk (k=0,1,2)的形式.
项的形式:
2个(a+b)都不选b得到的,因此a2出现的次数相当于从2个(a+b)中取0个b(即都取a)的组合数 ,即a2只有1个;
由1个 (a+b) 中选a,另1个 (a+b) 中选b得到的. 由于b选定后,a的选法也随之确定,因此,ab出现的次数相当于从2个 (a+b) 中取1个b的组合数 ,即ab共有2个.
由2个 (a+b) 中都选b得到的. 因此,b2出现的次数相当于从2个 (a+b) 中取2个b的组合数 ,即b2只有1个.
探究新知
探究新知
同样地,如何利用分步乘法计数原理解释(a+b)3 的展开式?
?
探究
a3
a2b
a2b
a2b
b3
ab2
ab2
ab2
展开式共有:
项的形式:
a4
a3b
ab3
b4
a2b2
探究新知
根据你发现的规律,你能写出(a+b)4 的展开式吗?
?
探究
解:
(项的结构)
探究新知
进一步地,你能写出(a+b)n 的展开式吗?
?
探究
(项的系数)
概念形成
上述公式叫做二项式定理,右边的多项式叫做 (a+b)n 的二项展开式,其中各项的系数 叫做二项式系数.
式中 的叫做二项展开式的通项,用 表示,即通项为展开式的第 项:
在二项式定理中,若设a=1, b=x,则得到公式
字母a按降幂排列,次数由n 递减到0;
字母b按升幂排列,次数由0递增到n.
例1
求 的展开式.
解:
典例分析
求 的展开式.
变式1:
解:
典例分析
例1 (1)求 (1+2x)7 的展开式的第4项;
(2)求 (1+2x)7 的展开式的第4项的系数;
(3)求 (1+2x)7 的展开式的第4项的二项式系数.
解:
(1)
(2)求 (1+2x)7 的展开式的第4项的系数为280.
(3)求 (1+2x)7 的展开式的第4项的二项式系数为 .
解:
的展开式的通项为
根据题意,得
因此, x2的系数是
求 的展开式中 x2 的系数.
例3
典例分析
解:
1.求 (2a+3b)6 的展开式的第3项.
巩固练习
2.求 的展开式的第r+1项.
解:
3.在 (x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含x4的项的系数是 .
-15
1.二项式定理
2.二项展开式的通项
3.二项式系数:
课堂小结
