北师大版数学七年级下册 6.3 第4课时 概率的简单应用 课件(共16张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 6.3 第4课时 概率的简单应用 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 370.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览

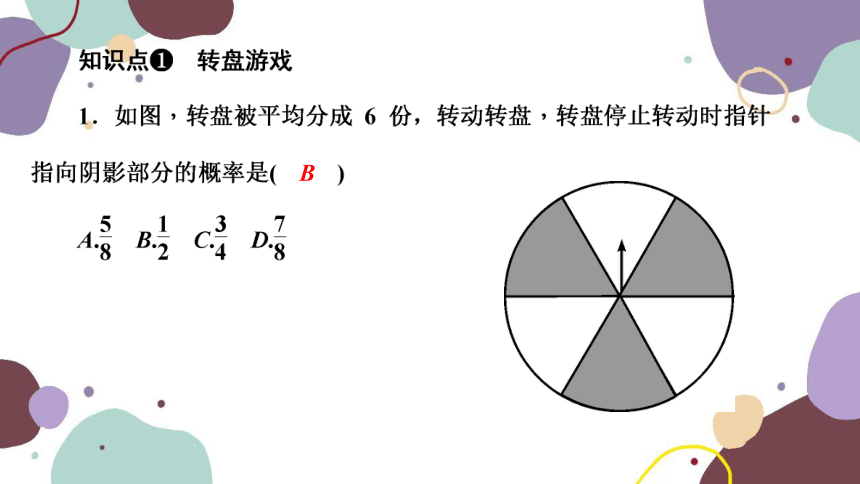




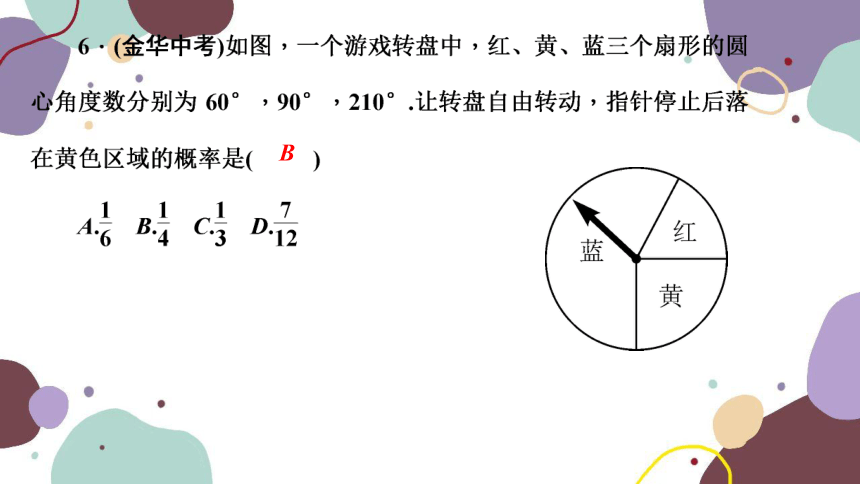
文档简介
(共16张PPT)
第六章 概率初步
6.3 等可能事件的概率
第4课时 概率的简单应用
B
D
3.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A,B,C,D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为______
4.如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动1次,求指针一次落在白色区域、落在黑色区域的概率.
B
B
D
11.飞镖随机地掷在下面的靶子上(图中圆的半径平分半圆).
12.如图是芳芳设计的自由转动的转盘,上面写有10个有理数.想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得整数;
(3)转得绝对值小于6的数.
13.如图,转盘被等分成六个扇形区域,并在上面依次写上数字:1,2,3,4,5,6.转盘指针的位置固定,转动转盘后任其自由停止.
(1)当停止转动时,指针指向奇数区域的概率是多少?
(2)请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为 ,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)
14.永辉超市进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 特等奖 一等奖 二等奖 三等奖
圆心角 1° 36° 53° 150°
促销公告:凡购买我商场商品均有可能获得下列大奖
特等奖:彩电一台
一等奖:自行车一辆
二等奖:圆珠笔一支
三等奖:卡通画一张
(1)获得圆珠笔的概率是多少?
(2)不获奖的概率是多少?
(3)如果不用转盘,请设计一种等效试验方案.(要求写清楚替代工具和实验规则)
(3)可采用“抓阄”或“抽签”等方法替代.在一个不透明的箱子里放进360个除标号不同外,其他均一样的乒乓球,其中一个标“特”,36个标“1”,53个标“2”,150个标“3”,其余不标数字,摸出标有哪个奖次的乒乓球,则获相应等级的奖品
第六章 概率初步
6.3 等可能事件的概率
第4课时 概率的简单应用
B
D
3.如图,把一个圆形转盘按1∶2∶3∶4的比例分成A,B,C,D四个扇形区域,自由转动转盘,停止后指针落在B区域的概率为______
4.如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.让转盘自由转动1次,求指针一次落在白色区域、落在黑色区域的概率.
B
B
D
11.飞镖随机地掷在下面的靶子上(图中圆的半径平分半圆).
12.如图是芳芳设计的自由转动的转盘,上面写有10个有理数.想想看,转得下列各数的概率是多少?
(1)转得正数;
(2)转得整数;
(3)转得绝对值小于6的数.
13.如图,转盘被等分成六个扇形区域,并在上面依次写上数字:1,2,3,4,5,6.转盘指针的位置固定,转动转盘后任其自由停止.
(1)当停止转动时,指针指向奇数区域的概率是多少?
(2)请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为 ,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)
14.永辉超市进行有奖促销活动.活动规则:购买500元商品就可以获得一次转转盘的机会(转盘分为5个扇形区域,分别是特等奖、一等奖、二等奖、三等奖、不获奖),转盘指针停在哪个获奖区域就可以获得该区域相应等级奖品一件.商场工作人员在制作转盘时,将获奖扇形区域圆心角分配如下表:
奖次 特等奖 一等奖 二等奖 三等奖
圆心角 1° 36° 53° 150°
促销公告:凡购买我商场商品均有可能获得下列大奖
特等奖:彩电一台
一等奖:自行车一辆
二等奖:圆珠笔一支
三等奖:卡通画一张
(1)获得圆珠笔的概率是多少?
(2)不获奖的概率是多少?
(3)如果不用转盘,请设计一种等效试验方案.(要求写清楚替代工具和实验规则)
(3)可采用“抓阄”或“抽签”等方法替代.在一个不透明的箱子里放进360个除标号不同外,其他均一样的乒乓球,其中一个标“特”,36个标“1”,53个标“2”,150个标“3”,其余不标数字,摸出标有哪个奖次的乒乓球,则获相应等级的奖品
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
