第7章相交线与平行线选择、填空题练习(河北地区专用)2021-2022学年下学期河北省各地冀教版七年级数学期中复习(Word版含解析)
文档属性
| 名称 | 第7章相交线与平行线选择、填空题练习(河北地区专用)2021-2022学年下学期河北省各地冀教版七年级数学期中复习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 700.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览


文档简介
第7章 相交线与平行线选择、填空题
一、单选题
1.(2021·河北张家口·七年级期中)如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
2.(2021·河北秦皇岛·七年级期中)如图,直线与相交于点,,若,则的度数为( ).
A. B. C. D.
3.(2021·河北沧州·七年级期中)如图,田地A的旁边有一条小河l,要想把小河里的水引到田地A处,为了省时省力需要作AB⊥l,垂足为B,沿AB挖水沟,则水沟最短,理由是( )
A.点到直线的距离 B.两点确定一条直线
C.垂线段最短 D.两点之间,线段最短
4.(2021·河北保定·七年级期中)如图,三条直线相交于点.若,,则的补角等于( )
A.150° B.34° C.56° D.146°
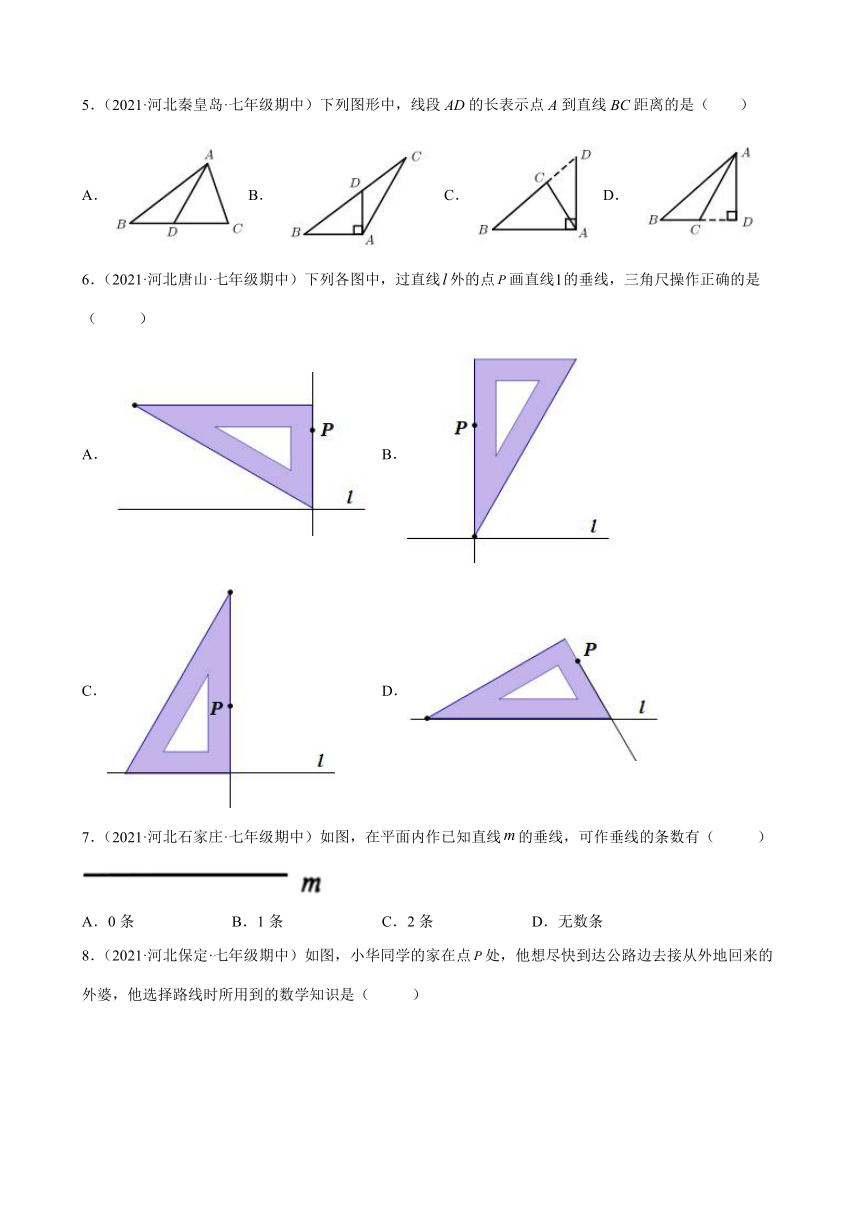
5.(2021·河北秦皇岛·七年级期中)下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B.C.D.
6.(2021·河北唐山·七年级期中)下列各图中,过直线外的点画直线的垂线,三角尺操作正确的是( )
A. B.
C. D.
7.(2021·河北石家庄·七年级期中)如图,在平面内作已知直线的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
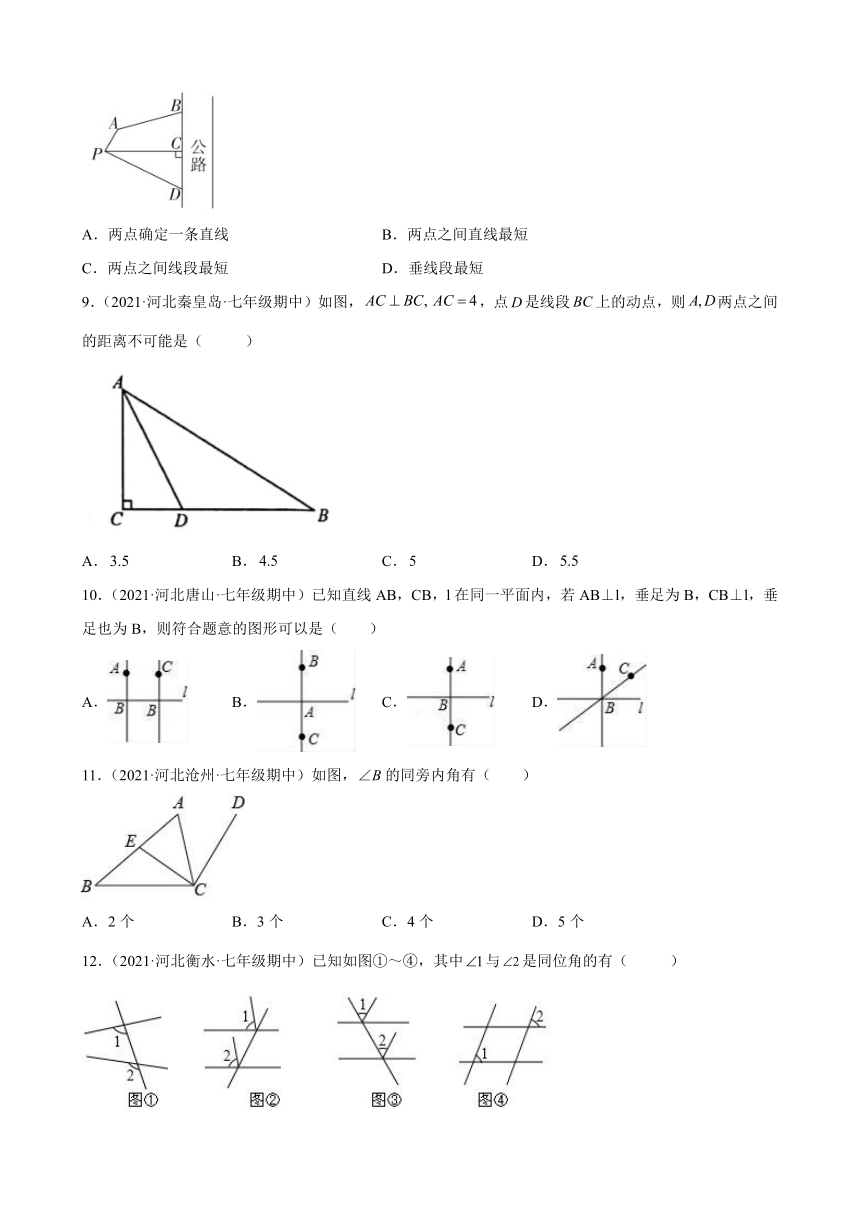
8.(2021·河北保定·七年级期中)如图,小华同学的家在点处,他想尽快到达公路边去接从外地回来的外婆,他选择路线时所用到的数学知识是( )
A.两点确定一条直线 B.两点之间直线最短
C.两点之间线段最短 D.垂线段最短
9.(2021·河北秦皇岛·七年级期中)如图,,点是线段上的动点,则两点之间的距离不可能是( )
A. B. C. D.
10.(2021·河北唐山·七年级期中)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A. B. C. D.
11.(2021·河北沧州·七年级期中)如图,∠B的同旁内角有( )
A.2个 B.3个 C.4个 D.5个
12.(2021·河北衡水·七年级期中)已知如图①~④,其中与是同位角的有( )
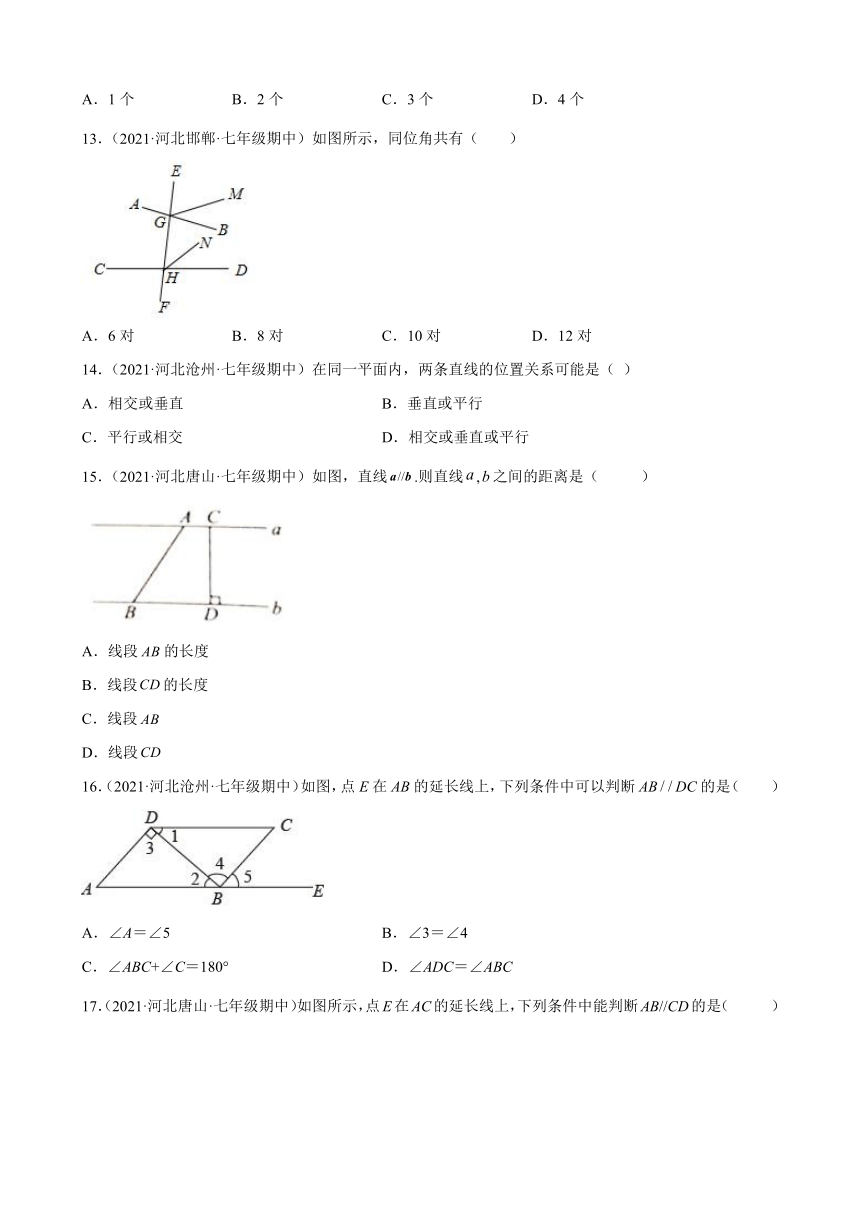
A.1个 B.2个 C.3个 D.4个
13.(2021·河北邯郸·七年级期中)如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
14.(2021·河北沧州·七年级期中)在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.相交或垂直或平行
15.(2021·河北唐山·七年级期中)如图,直线.则直线,之间的距离是( )
A.线段的长度
B.线段的长度
C.线段
D.线段
16.(2021·河北沧州·七年级期中)如图,点E在AB的延长线上,下列条件中可以判断ABDC的是( )
A.∠A=∠5 B.∠3=∠4
C.∠ABC+∠C=180° D.∠ADC=∠ABC
17.(2021·河北唐山·七年级期中)如图所示,点E在AC的延长线上,下列条件中能判断AB//CD的是( )
A. B. C. D.
18.(2021·河北唐山·七年级期中)如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
19.(2021·河北张家口·七年级期中)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
20.(2021·河北邢台·七年级期中)如图,把三根木条钉在一起,使之可以在连接点M,N处自由旋转,若,,则如何旋转木条才能使它与木条平行.
小明说:把木条绕点M逆时针旋转10°;
小刚说:把木条绕点M顺时针旋转170°.
以下说法正确的是( )
A.小明的操作正确,小刚的操作错误 B.小明的操作错误,小刚的操作正确
C.小明和小刚的操作都正确 D.小明和小刚的操作都错误
21.(2021·河北沧州·七年级期中)如图,把三角尺的直角顶点放在直尺的一边上,若∠2=58°,则∠1的度数为( )
A.58° B.48° C.42° D.32°
22.(2021·河北保定·七年级期中)如图,下列推理正确的是( )
A.∵AB∥CD,∴∠B=∠DCE(两直线平行,同位角相等)
B.∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行)
C.∵AD∥BC,∴∠3=∠4(内错角相等,两直线平行)
D.∵∠B+∠BCD=180°,∴AD∥BC(同旁内角互补,两直线平行)
23.(2021·河北张家口·七年级期中)如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.125° B.130° C.135° D.145°
24.(2021·河北·香河县第九中学八年级期中)一副三角板如图方式摆放,点D在直线上,且,则的度数是( )
A. B. C. D.
25.(2021·河北保定·七年级期中)把一副直角三角尺按如图方式摆放,点与点重合,边与边都在直线上,若直线,且经过点,则( )
A. B. C. D.
26.(2021·河北唐山·七年级期中)如图,AB∥CD,AC⊥BC,CE⊥AB于点E,则图中与∠1互余的角的个数是( )
A.1 B.2 C.3 D.5
27.(2021·河北沧州·七年级期中)如图,已知ABCD,∠ECA=120°,∠ECD=120°,∠A的度数是( )
A.30° B.45° C.60° D.65°
28.(2021·河北沧州·七年级期中)下列四个图中,∠1=∠2一定成立的是( )
A. B. C. D.
29.(2021·河北秦皇岛·七年级期中)将直尺和直角三角板按如图方式摆放(∠ACB为直角),已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
30.(2021·河北邯郸·七年级期中)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)相等的两个角是对顶角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
31.(2021·河北唐山·七年级期中)下列句子,是命题的是( )
A.美丽的天空 B.相等的角是对顶角
C.作线段AB=CD D.你喜欢运动吗?
32.(2021·河北·邯郸市第二十三中学九年级期中)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
33.(2021·河北秦皇岛·七年级期中)下列命题中是假命题的是( )
A.对顶角相等 B.同旁内角互补 C.两点确定一条直线 D.垂线段最短
34.(2021·河北张家口·七年级期中)有下列命题,其中假命题有( )
①内错角相等.
②在同一平面内,垂直于同一条直线的两直线平行.
③相等的角是对顶角.
④经过直线外一点,有且只有一条直线与已知直线平行.
A.①② B.①③ C.②④ D.③④
35.(2021·河北唐山·八年级期中)下列命题的逆命题是真命题的是( )
A.若,则 B.同位角相等,两直线平行
C.对顶角相等 D.若,,则
36.(2021·河北张家口·七年级期中)下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.同旁内角互补
37.(2021·河北唐山·七年级期中)如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
38.(2021·河北唐山·七年级期中)在下面的四幅图案中,能通过图案(1)平移得到的是( )
A. B. C. D.
39.(2021·河北沧州·七年级期中)四根火柴棒摆成如图所示的象形“口”字,平移此象形字火柴棒后,变成的象形文字正确的是( )
A. B. C. D.
40.(2021·河北唐山·八年级期中)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
41.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,若图形经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
A.向右平移4格,再向下平移4格
B.向右平移6格,再向下平移5格
C.向右平移4格,再向下平移3格
D.向右平移5格,再向下平移3格
42.(2021·河北秦皇岛·七年级期中)如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42 B.96 C.84 D.48
43.(2021·河北秦皇岛·七年级期中) 某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
二、填空题
44.(2021·河北张家口·七年级期中)如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOD=120°,则∠BOD=__________°.
45.(2021·河北邯郸·七年级期中)如图,直线AB与CD相交于点O,,若,则=______°.
46.(2021·河北张家口·七年级期中)如图,已知相交于点,,,则的度数是__________.
47.(2021·河北邯郸·七年级期中)如图,直线AB、CD相交于点O,若,则等于______________.
48.(2021·河北唐山·七年级期中)如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB=_______.
49.(2021·河北唐山·七年级期中)一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
50.(2021·河北邢台·七年级期中)如图,已知,,所以点三点共线的理由__________.
51.(2021·河北张家口·七年级期中)如图,一个宽度相等的纸条按如图所示方法折叠一下,则________度.
52.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,直线,则__________.
53.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,直线,被直线所截,,.若,则等于___________.
54.(2021·河北秦皇岛·七年级期中)将一副三角板如图放置,∠ECD=∠BAC=90°,使点A在DE上,BC//DE,则∠ACE的度数为_______.
55.(2021·河北秦皇岛·七年级期中)将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为_________________________________________________.
56.(2021·河北·青龙满族自治县教师发展中心八年级期中)请写出“两直线平行,同位角相等”的逆命题:_____________________________.
57.(2021·河北唐山·八年级期中)命题“全等三角形的对应角相等”的逆命题是_____命题.(填“真”或“假”)
58.(2021·河北张家口·七年级期中)若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠B=_____度.
59.(2021·河北唐山·八年级期中)如图,将沿方向平移至处.若,则=___.
60.(2021·河北沧州·七年级期中)如图,在三角形ABC中,∠C=90°,AC+BC=31,AB=25,则内部五个小直角三角形周长的和为_______.
61.(2021·河北唐山·七年级期中)边长为4的等边与等边互相重合,将沿直线L向左平移m个单位长度,将向右也平移m个单位长度,若,则m=________;若C、E是线段BF的三等分点时,m=________.
62.(2021·河北唐山·七年级期中)某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯.已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面如图所示,则购买地毯至少需要___________元.
试卷第1页,共3页
参考答案:
1.C
【解析】
根据对顶角的定义,可得答案.
A、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故A选项错误;
B、∠1与∠2没有公共顶点,不是对顶角,故B选项错误;
C、∠1与∠2的两边互为反向延长线,是对顶角,故C选项正确;
D、∠1与∠2的两边不是互为反向延长线,不是对顶角,故D选项错误.
故选:C.
【点睛】
本题考查了对顶角,利用∠1的两边与∠2的两边互为反向延长线是解题的关键.
2.C
【解析】
试题分析::∵∠AOE=140°,∠AOE和∠2是邻补角,
∴∠2=180°-140°=40°,
∵∠1=∠2,∴∠BOD=2∠2=80°,
又∵∠BOD和∠AOC是对顶角
∴∠AOC=∠BOD=80°.
故选C.
考点:1.邻补角2.对顶角.
3.C
【解析】
根据垂线段最短即可得.
解:于点,
沿挖水沟,则水沟最短,理由是垂线段最短,
故选:C.
【点睛】
本题考查了垂线段最短,掌握理解垂线段最短是解题关键.
4.D
【解析】
根据垂线的定义求出∠3,然后利用对顶角相等和补角的定义解答.
解:∵CO⊥AB,∠1=56°,
∴∠3=90° ∠1=90° 56°=34°,
∴∠2=∠3=34°,
∴的补角等于146°,
故选:D.
【点睛】
本题考查了垂线的定义,对顶角相等的性质以及补角的定义,是基础题,掌握两个角的和为180°,则称这两个角互补,是解题的关键.
5.D
【解析】
根据点到直线的距离定义逐项判断即可.
解:A中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
B中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
C中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
D中的AD⊥BC,所以线段AD的长是点A到直线BC距离,故此选项正确,
故选:D.
【点睛】
本题考查点到直线的距离定义,熟知点到直线的距离定义是解答的关键.
6.C
【解析】
根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线即可;
根据分析可得C的画法正确;
故答案选C.
【点睛】
本题主要考查了垂线的作法,准确理解是解题的关键.
7.D
【解析】
在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.
在同一平面内,画已知直线的垂线,可以画无数条;
故选:D.
【点睛】
此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.
8.D
【解析】
根据垂线段的性质解答即可.
解:小华同学应选择→路线,因为垂线段最短,
故选:D.
【点睛】
本题考查了垂线段的性质,解题的关键是掌握垂线段的性质.
9.A
【解析】
根据垂线段最短可得AD≥4,进而可得答案.
解:∵AC=4,AC⊥BC于点C,
∴,
故选:A.
【点睛】
本题主要考查了垂线段的性质,解题的关键是掌握垂线段最短.
10.C
【解析】
试题分析:根据题意画出图形即可.
解:根据题意可得图形,
故选C.
点评:此题主要考查了垂线,关键是掌握垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
11.D
【解析】
根据同旁内角的定义(两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角叫做同旁内角)即可得.
解:的同旁内角有,共5个,
故选:D.
【点睛】
本题考查了同旁内角,熟记定义是解题关键.
12.B
【解析】
根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角可得答案.
解:图①中∠1与∠2是同位角,
图②中∠1与∠2不是同位角,
图③中∠1与∠2是同位角,
图④中∠1与∠2不是同位角,
故选:B.
【点睛】
此题主要考查了同位角,关键是掌握同位角的边构成“F“形.
13.C
【解析】
根据同位角的定义,进行分析求解即可得到答案.
解:如图所示
由AB、CD、EF组成的“三线八角”中同位角有四对;
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选C.
【点睛】
本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
14.C
【解析】
根据两条直线有一个交点的直线是相交线,没有交点的直线是平行线,可得答案.
在同一平面内,两条直线有一个交点,两条直线相交;在同一平面内,两条直线没有交点,两条直线平行,故C正确;
故选:C.
【点睛】
本题主要考查了同一平面内,两条直线的位置关系,注意垂直是相交的一种特殊情况,不能单独作为一类.
15.B
【解析】
根据平行线间的距离的定义,可得答案.
解:∵直线a∥b,CD⊥b,
∴直线a,b之间距离是线段CD的长度,
故选B.
【点睛】
本题考查了平行线间的距离,熟知平行线间的距离的定义是解题关键.
16.C
【解析】
根据平行线的判定逐项判断即可得.
A、由可得,则此项不符合题意;
B、由可得,则此项不符合题意;
C、由可得,则此项符合题意;
D、由不能判断,则此项不符题意;
故选:C.
【点睛】
本题考查了平行线的判定,熟练掌握平行线的判定方法是解题关键.
17.B
【解析】
根据平行线的判定逐项判断即可.
解:A、∵∠3=∠4,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意;
B、∵∠1=∠2,
∴AB∥CD,此选项符合题意;
C、∵,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意;
D、∵,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意,
故选:B.
【点睛】
本题考查平行线的判定,熟练掌握平行线的判定是解答的关键.
18.C
【解析】
根据平行线的判定定理判断即可.
∵,∴a∥b,∴A选项不符合题意;
∵,∴a∥b,∴B选项不符合题意;
∵,∴a∥b,∴D选项不符合题意;
∵,无法判断a∥b,∴C选项符合题意;
故选C.
【点睛】
本题考查了平行线的判定定理,熟记平行线判定定理是解题的关键.
19.B
【解析】
根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意得:两次拐的方向不相同,但角度相等.
解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
因此,第一次与第二次拐的方向不相同,角度要相同,
故只有B选项符合,
故选B.
【点睛】
此题主要考查了平行线的性质,注意要想两次拐弯后,仍在原来的方向上平行前进,则拐的方向应相反,角度应相等.
20.C
【解析】
根据小明小刚的描述,两种操作的结果都能使∠1=60°,可得结果.
解:根据小明的操作,把木条绕点M逆时针旋转10°,则,根据同位角相等,两直线平行,故;根据小刚的操作,如解图,把木条绕点M顺时针旋转170°,则,即.同理可得,.因此,小明和小刚的操作都正确.
故选C.
【点睛】
本题考查了平行线的判定,同位角相等,两直线平行.
错因分析 容易题.失分的原因是:1.没有掌握平行线的判定,其中同位角或内错角相等、同旁内角互补,两直线平行.2.没有掌握旋转的基本性质.
21.D
【解析】
如图(见解析),先根据平行线的性质可得,再根据平角的定义即可得.
解:如图,由题意得:,
,
又,
,
,
故选:D.
【点睛】
本题考查了平行线的性质、平角的定义等知识点,熟练掌握平行线的性质是解题关键.
22.A
【解析】
根据平行线的判定与性质逐一进行判断推理即可.
解:∵AB//CD,∴∠B=∠DCE(两直线平行,同位角相等),故A正确;
∵∠1=∠2,∴AB//CD(内错角相等,两直线平行),故B错误;
∵AD//BC,∴∠3=∠4(两直线平行,内错角相等),故C错误;
∵∠B+∠BCD=180°,∴AB//CD(同旁内角互补,两直线平行),故D错误.
故选:A.
【点晴】
考查了平行线的判定与性质,解题关键是仔细观察图形灵活运用平行线的判定与性质进行推理.
23.C
【解析】
根据两直线平行,同位角相等可得∠3=∠2,再根据邻补角的定义解答.
如图,
∵a∥b,∠2=45°,
∴∠3=∠2=45°,
∴∠1=180° ∠3=135°,
故选:C.
【点睛】
本题考查了平行线的性质,解题的关键是掌握平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
24.A
【解析】
根据三角板自带角的度数以及平行的性质可得.
解:∵AB∥EF,
∴∠ADE=∠DAB=∠DAC+∠CAB=45°+30°=75°,
又∵∠ADC=90°,
∴∠CDF=180°-∠ADC-∠ADE=15°
故选 A.
【点睛】
本题考查了三角板的认识和平行线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
25.D
【解析】
根据题意易得,然后根据平角的定义可得,进而根据平行线的性质可求解.
解:由题意得:,
∵,
∴,
∵,
∴;
故选D.
【点睛】
本题主要考查平行线的性质,熟练掌握平行线的性质是解题的关键.
26.C
【解析】
由AB∥CD得∠1=∠2,∠B=∠3,根据平行线的推论得EC⊥CD,再由余角的性质得∠1与∠ACE、∠B、∠3三个角互余,进而即可得到答案.
解:如图所示:
∵AB∥CD,
∴∠1=∠2,
又∵EC⊥AB,
∴EC⊥CD,
∴∠2+∠ACE=90°,
∴∠1+∠ACE=90°,
∴∠1与∠ACE互余;
又∵AC⊥BC,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
又∵∠1=∠CAB,
∴∠1+∠B=90°,
∴∠1与∠B互余;
又∵AB∥CD,
∴∠B=∠3,
∴∠1+∠3=90°,
∴∠1与∠3互余,
综合所述,图中与∠1互余的角的个数为3,
故选:C.
【点睛】
本题综合考查了平行线的性质,垂直的定义,对顶角的性质,余角的性质等相关知识点,重点掌握平行线的性质,难点是找余角的个数时不重不漏.
27.C
【解析】
先求出,再根据平行线的性质即可得.
解:,
,
,
,
故选:C.
【点睛】
本题考查了平行线的性质等知识点,熟练掌握平行线的性质是解题关键.
28.D
【解析】
根据平行线的性质、对顶角相等即可得.
A、当两个角的两边互相平行时,一定成立,则此项不符题意;
B、如图,当时,一定成立,则此项不符题意;
C、如图,,当时,一定成立,则此项不符题意;
D、由对顶角相等得:一定成立,则此项符合题意;
故选:D.
【点睛】
本题考查了平行线的性质、对顶角相等,熟练掌握对顶角相等是解题关键.
29.C
【解析】
试题分析:先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.∵∠1+∠3=90°,
∠1=30°,∴∠3=60°. ∵直尺的两边互相平行, ∴∠2=∠3=60°.
考点:平行线的性质
30.B
【解析】
(1)根据平行线的性质进行判断即可;
(2)根据对顶角的概念进行判断即可;
(3)根据平行公理的推论进行判断即可;
(4)根据垂线段的概念进行判断即可.
解:(1)只有两条平行线被第三条直线所截,同位角才相等,故此说法错误;
(2)相等的角不一定是对顶角,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,故此说法错误;
(3)假设它与另一条平行,根据平行于同一直线的两直线平行可得它与第一条也平行,这与已知条件相矛盾,故平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,此说法正确;
(4)从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故此说法错误.
故正确的说法有1个.
故选B.
【点睛】
本题主要考查了平行线的性质,对顶角的概念,平行公理的推论及垂线段的概念,熟记这些定理及概念是解决此题的关键.
31.B
【解析】
判断事物的语句叫命题,根据命题的定义逐一进行判断即可得到答案.
解:A、美丽的天空,是描叙性语言,它不是命题,所以A选项不符合题意;
B、相等的角是对顶角是命题,所以B选项符合题意;
C、作线段AB=CD,是描叙性语言,它不是命题,所以C选项不符合题意;
D、你喜欢运动吗?,是疑问句,没有对事物作出判断,它不是命题,所以D选项不符合题意.
故选:B.
【点睛】
本题考查了命题的定义,掌握根据命题的定义进行命题的判断是解题的关键.
32.A
【解析】
反证法的第一步就是假设命题反面成立
用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”,第一步应先假设∠B≥90°;
故选:A
【点睛】
本题考查反正法的步骤:1、假设命题反面成立;2、从假设出发,经过推理得出和反面命题矛盾,或者与定义、公理、定理矛盾;3、得出假设命题不成立是错误的,即所求证命题成立
33.B
【解析】
根据平行线的性质、对顶角的性质、直线的概念、垂线段的性质定理判断.
A、对顶角相等,本选项说法是真命题;
B、两直线平行,同旁内角才互补,故本选项说法是假命题;
C、两点确定一条直线,本选项说法是真命题;
D、垂线段最短,本选项说法是真命题;
故选:B.
【点睛】
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
34.B
【解析】
利用平行线的性质、对顶角的定义及平行公理分别判断后即可确定正确的选项.
①两直线平行,内错角相等,故原命题错误,是假命题,符合题意.
②在同一平面内,垂直于同一条直线的两直线平行,正确,是真命题,不符合题意.
③相等的角不一定是对顶角,故原命题错误,是假命题,符合题意.
④经过直线外一点,有且只有一条直线与已知直线平行,正确,是真命题,不符合题意.
故选:B.
【点睛】
本题考查命题与定理的知识,解题的关键是了解平行线的性质、对顶角的定义以及平行公理.
35.B
【解析】
分别写出原命题的逆命题,然后判断真假即可.
解:A、若,则的逆命题是若,则,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若,,则的逆命题是若,则,,逆命题是假命题,不符合题意;
故选:B.
【点睛】
本题考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题,难度不大.
36.D
【解析】
根据线段、对顶角、补角、平行线的性质判断即可.
解:A、两点之间,线段最短,是真命题;
B、对顶角相等,是真命题;
C、直角的补角仍然是直角,是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补,是假命题;
故选:D.
【点睛】
此题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
37.A
【解析】
观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE,进而可得答案.
解:根据平移的性质,
易得平移的距离=BE=8-5=3cm,
故选:A.
【点睛】
本题考查平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,本题关键要找到平移的对应点.
38.C
【解析】
平移前后形状与大小没有改变,并且对应点的连线平行且相等的图形即可.
解:A、对应点的连线相交,不能通过平移得到,不符合题意;
B、对应点的连线相交,不能通过平移得到,不符合题意;
C、可通过平移得到,符合题意;
D、对应点的连线相交,不能通过平移得到,不符合题意;
故选:C.
【点睛】
本题考查了平移变换,解题的关键是熟练掌握平移变换的性质,属于中考常考题型.
39.C
【解析】
根据火柴头的方向、平移的定义即可得.
解:此象形字火柴棒中,有两根火柴头朝向左,一根火柴头朝向上,一根火柴头朝向下,
因为平移不改变火柴头的朝向,
所以观察四个选项可知,只有选项C符合,
故选:C.
【点睛】
本题考查了平移,掌握理解平移的概念是解题关键.
40.A
【解析】
解:根据网格结构,观察点对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,
所以,平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选A.
41.A
【解析】
根据图形A与下方图形中空白部分的位置解答即可.
解:由图可知,正确的平移方式是向右平移4格,再向下平移4格.
故选A.
【点睛】
本题考查平移特征,掌握平移特征是解题关键.
42.D
【解析】
根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S四边形ODFC=S梯形ABEO,根据梯形的面积公式即可求解。
由平移的性质知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE) BE=×(10+6)×6=48.
故选D.
【点睛】
本题考查平移的性质,平移前后两个图形大小,形状完全相同,图形上的每个点都平移了相同的距离,对应点之间的距离就是平移的距离.
43.D
【解析】
试题分析:
解:由图形可得出:甲所用铁丝的长度为:2a+2b,
乙所用铁丝的长度为:2a+2b,
丙所用铁丝的长度为:2a+2b,
故三种方案所用铁丝一样长.
故选D.
考点:生活中的平移现象
44.30
【解析】
先利用补角的定义求出∠EOC=60°,再根据角平分线的性质计算.
解:∵∠EOD=120°,
∴∠EOC=60°(邻补角定义).
∵OA平分∠EOC,
∴∠AOC=∠EOC=30°(角平分线定义),
∴∠BOD=30°(对顶角相等).
故答案为:30.
【点睛】
本题考查由角平分线的定义,结合补角的性质,易求该角的度数.
45.35°
【解析】
先根据垂直的定义和角的和差求出∠BOD的度数,再根据对顶角相等的性质解答即可.
解:∵,
∴∠BOM=90°,
∵,
∴∠BOD=90°-55°=35°,
∴∠AOC=∠BOD=35°,
故答案为:35.
【点睛】
本题考查了垂直的定义、对顶角的性质和角的和差计算,属于基础题目,熟练掌握基本知识是解题的关键.
46.
【解析】
依据、、相交于点,,,即可得到,再根据对顶角相等,即可得出.
解:、、相交于点,,,
,
又与是对顶角,
,
故答案为:.
【点睛】
本题考查了对顶角相等的性质,平角的定义,解题的关键是准确识图.
47.130°
【解析】
根据对顶角相等可得∠1=∠2,再求出∠1,然后根据邻补角的定义列式计算即可得.
解:由对顶角相等可得,∠1=∠2,
∵∠1+∠2=100°,
∴∠1=50°,
∴∠BOC=180° ∠1=180° 50°=130°
故答案为:130°
【点睛】
本题考查对顶角、邻补角,关键是熟记对顶角的性质和邻补角的定义.
48.128°##128度
【解析】
根据垂直的定义得出∠AOE=90°,最后根据∠COB=∠AOD=∠AOE +∠EOD进行求解.
∵OE⊥AB,∠EOD=38°,
∴∠AOE=90°,
∴∠COB=∠AOD=∠AOE +∠EOD=90°+38°=128°,
故答案为:128°.
【点睛】
本题考查垂直的定义,对顶角的性质,熟练掌握对顶角相等是解题的关键.
49.270°
【解析】
过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
【点睛】
本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
50.平行公理的推论
【解析】
根据平行公理的推论即可得.
平行公理的推论:平行于同一条直线的两条直线互相平行
则点三点共线
故答案为:平行公理的推论.
【点睛】
本题考查了平行公理的推论,熟记平行公理的推论是解题关键.
51.65
【解析】
根据两直线平行内错角相等,以及折叠关系列出方程求解则可.
解:如图,由题意可知,
AB∥CD,
∴∠1+∠2=130°,
由折叠可知,∠1=∠2,
∴2∠1=130°,
解得∠1=65°.
故答案为:65.
【点睛】
本题考查了平行线的性质和折叠的知识,题目比较灵活,难度一般.
52.
【解析】
过点C作CD∥a,则CD∥b,利用平行线的性质求解即可
如图,过点C作CD∥a,
∵直线,
∴CD∥b,
∴∠ACD=30°,∠DCB=50°,
∴∠ACB=∠ACD+∠DCB =30°+50°=80°,
故答案为:80°.
【点睛】
本题考查了平行线的判定,平行线的性质,角的和,熟练构造平行线辅助线,活用平行线的判定与性质是解题的关键.
53.
【解析】
由a∥b得,,由∠3+∠1+∠2=180°及已知,可求得∠1的度数,从而可得结果.
∵a∥b
∴
∵∠3+∠1+∠2=180°,,
∴
∴
故答案为:
【点睛】
本题考查了平行线的性质.
54.15°
【解析】
根据两直线平行,内错角相等求出∠BCE=∠E=30°,然后求出∠ACE的度数.
∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACE=∠ACB ∠BCE=45° 30°=15°,
故答案为:15°.
【点睛】
本题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.
55.如果两条直线平行于同一条直线,那么这两条直线平行
【解析】
命题由题设和结论两部分组成,通常写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.
命题可以改写为:如果两条直线平行于同一条直线,那么这两条直线平行.
故答案为:如果两条直线平行于同一条直线,那么这两条直线平行
【点睛】
任何一个命题都可以写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.在改写过程中,不能简单地把题设部分、结论部分分别塞在“如果”、“那么”后面,要适当增减词语,保证句子通顺而不改变原意.
56.如果同位角相等,那么两直线平行
【解析】
命题是由题设和结论两部分组成的,把原命题的题设作结论,原命题的结论作题设,这样就将原命题变成了它的逆命题.
解:原命题是:两直线平行,同位角相等.
改成如果…那么…的形式为:如果两直线平行,那么同位角相等.
∴逆命题为:如果同位角相等,那么两直线平行,
故答案为:如果同位角相等,那么两直线平行.
【点睛】
本题是一道命题与定理的概念试题,考查了命题的组成,原命题与逆命题的关系.
57.假
【解析】
首先分清题设是:两个三角形全等,结论是:对应角相等,把题设与结论互换即可得到逆命题,然后判断正误即可.
解:“全等三角形的对应角相等”的题设是:两个三角形全等,结论是:对应角相等,因而逆命题是:对应角相等的三角形全等.是一个假命题.
故答案为:假.
【点睛】
本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
58.55或20
【解析】
根据平行线性质得出∠A+∠B=180°①,∠A=∠B②,求出∠A=3∠B﹣40°③,把③分别代入①②求出即可.
解:∵∠A与∠B的两边分别平行,
∴∠A+∠B=180°①,∠A=∠B②,
∵∠A比∠B的3倍少40°,
∴∠A=3∠B﹣40°③,
把③代入①得:3∠B﹣40°+∠B=180°,
∠B=55°,
把③代入②得:3∠B﹣40°=∠B,
∠B=20°,
故答案为:55或20.
【点睛】
本题考查平行线的性质,解题的关键是掌握由∠A和∠B的两边分别平行,即可得∠A =∠B或∠A+∠B=180° ,注意分类讨论思想的应用.
59.3
【解析】
根据平移的性质得到,再用得到的长,从而得到的长.
解:∵沿方向平移至处,
∴,
∵,
∴,
∴,
∴,
故答案为3.
【点睛】
本题考查了平移的性质,解题的关键是掌握把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
60.56
【解析】
先根据平移的性质可得内部五个小直角三角形的直角边的和等于,再根据三角形的周长公式即可得.
解:由题意得:内部五个小直角三角形的直角边的和等于,
则内部五个小直角三角形周长的和为,
故答案为:56.
【点睛】
本题考查了平移的性质等知识点,熟练掌握平移的性质是解题关键.
61. 5 1或4
【解析】
由平移的性质可知,可得m的值;若C、E是线段BF的三等分点时,
将沿直线L向左平移m个单位长度,将向右也平移m个单位长度,两个三角形完全不重叠时,由平移的性质可知,可得m的值;两个三角形部分重叠时,,,可得m值.
解:由平移的性质可知;
如图,两个三角形完全不重叠时,因为C、E是线段BF的三等分点,所以,由平移的性质可知,所以;
如图,两个三角形部分重叠时,因为C、E是线段BF的三等分点,,
综上所述,m的值为1或4.
故答案为(1)5 (2) 1或4
【点睛】
本题考查了平移的性质,熟练掌握平移的距离即为对应点所连线段的长度这一性质是解题的关键.
62.512
【解析】
根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为5.5米,2.5米,
∴地毯的长度为2.5+5.5=8米,地毯的面积为8×2=16平方米,
∴买地毯至少需要16×32=512元.
故答案为:512
【点睛】
本题考查了平移的应用,解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
答案第1页,共2页
一、单选题
1.(2021·河北张家口·七年级期中)如图,∠1与∠2构成对顶角的是( )
A. B.
C. D.
2.(2021·河北秦皇岛·七年级期中)如图,直线与相交于点,,若,则的度数为( ).
A. B. C. D.
3.(2021·河北沧州·七年级期中)如图,田地A的旁边有一条小河l,要想把小河里的水引到田地A处,为了省时省力需要作AB⊥l,垂足为B,沿AB挖水沟,则水沟最短,理由是( )
A.点到直线的距离 B.两点确定一条直线
C.垂线段最短 D.两点之间,线段最短
4.(2021·河北保定·七年级期中)如图,三条直线相交于点.若,,则的补角等于( )
A.150° B.34° C.56° D.146°
5.(2021·河北秦皇岛·七年级期中)下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.B.C.D.
6.(2021·河北唐山·七年级期中)下列各图中,过直线外的点画直线的垂线,三角尺操作正确的是( )
A. B.
C. D.
7.(2021·河北石家庄·七年级期中)如图,在平面内作已知直线的垂线,可作垂线的条数有( )
A.0条 B.1条 C.2条 D.无数条
8.(2021·河北保定·七年级期中)如图,小华同学的家在点处,他想尽快到达公路边去接从外地回来的外婆,他选择路线时所用到的数学知识是( )
A.两点确定一条直线 B.两点之间直线最短
C.两点之间线段最短 D.垂线段最短
9.(2021·河北秦皇岛·七年级期中)如图,,点是线段上的动点,则两点之间的距离不可能是( )
A. B. C. D.
10.(2021·河北唐山·七年级期中)已知直线AB,CB,l在同一平面内,若AB⊥l,垂足为B,CB⊥l,垂足也为B,则符合题意的图形可以是( )
A. B. C. D.
11.(2021·河北沧州·七年级期中)如图,∠B的同旁内角有( )
A.2个 B.3个 C.4个 D.5个
12.(2021·河北衡水·七年级期中)已知如图①~④,其中与是同位角的有( )
A.1个 B.2个 C.3个 D.4个
13.(2021·河北邯郸·七年级期中)如图所示,同位角共有( )
A.6对 B.8对 C.10对 D.12对
14.(2021·河北沧州·七年级期中)在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.相交或垂直或平行
15.(2021·河北唐山·七年级期中)如图,直线.则直线,之间的距离是( )
A.线段的长度
B.线段的长度
C.线段
D.线段
16.(2021·河北沧州·七年级期中)如图,点E在AB的延长线上,下列条件中可以判断ABDC的是( )
A.∠A=∠5 B.∠3=∠4
C.∠ABC+∠C=180° D.∠ADC=∠ABC
17.(2021·河北唐山·七年级期中)如图所示,点E在AC的延长线上,下列条件中能判断AB//CD的是( )
A. B. C. D.
18.(2021·河北唐山·七年级期中)如图,在下列条件中,不能判定直线与平行的是( )
A. B. C. D.
19.(2021·河北张家口·七年级期中)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的度数是( )
A.第一次右拐50°,第二次左拐130° B.第一次左拐50°,第二次右拐50°
C.第一次左拐50°,第二次左拐130° D.第一次右拐50°,第二次右拐50°
20.(2021·河北邢台·七年级期中)如图,把三根木条钉在一起,使之可以在连接点M,N处自由旋转,若,,则如何旋转木条才能使它与木条平行.
小明说:把木条绕点M逆时针旋转10°;
小刚说:把木条绕点M顺时针旋转170°.
以下说法正确的是( )
A.小明的操作正确,小刚的操作错误 B.小明的操作错误,小刚的操作正确
C.小明和小刚的操作都正确 D.小明和小刚的操作都错误
21.(2021·河北沧州·七年级期中)如图,把三角尺的直角顶点放在直尺的一边上,若∠2=58°,则∠1的度数为( )
A.58° B.48° C.42° D.32°
22.(2021·河北保定·七年级期中)如图,下列推理正确的是( )
A.∵AB∥CD,∴∠B=∠DCE(两直线平行,同位角相等)
B.∵∠1=∠2,∴AD∥BC(内错角相等,两直线平行)
C.∵AD∥BC,∴∠3=∠4(内错角相等,两直线平行)
D.∵∠B+∠BCD=180°,∴AD∥BC(同旁内角互补,两直线平行)
23.(2021·河北张家口·七年级期中)如图,直线a,b被直线c所截,a∥b,若∠2=45°,则∠1等于( )
A.125° B.130° C.135° D.145°
24.(2021·河北·香河县第九中学八年级期中)一副三角板如图方式摆放,点D在直线上,且,则的度数是( )
A. B. C. D.
25.(2021·河北保定·七年级期中)把一副直角三角尺按如图方式摆放,点与点重合,边与边都在直线上,若直线,且经过点,则( )
A. B. C. D.
26.(2021·河北唐山·七年级期中)如图,AB∥CD,AC⊥BC,CE⊥AB于点E,则图中与∠1互余的角的个数是( )
A.1 B.2 C.3 D.5
27.(2021·河北沧州·七年级期中)如图,已知ABCD,∠ECA=120°,∠ECD=120°,∠A的度数是( )
A.30° B.45° C.60° D.65°
28.(2021·河北沧州·七年级期中)下列四个图中,∠1=∠2一定成立的是( )
A. B. C. D.
29.(2021·河北秦皇岛·七年级期中)将直尺和直角三角板按如图方式摆放(∠ACB为直角),已知∠1=30°,则∠2的大小是( )
A.30° B.45° C.60° D.65°
30.(2021·河北邯郸·七年级期中)给出下列说法:
(1)两条直线被第三条直线所截,同位角相等;
(2)相等的两个角是对顶角;
(3)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交;
(4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离;
其中正确的有( )
A.0个 B.1个 C.2个 D.3个
31.(2021·河北唐山·七年级期中)下列句子,是命题的是( )
A.美丽的天空 B.相等的角是对顶角
C.作线段AB=CD D.你喜欢运动吗?
32.(2021·河北·邯郸市第二十三中学九年级期中)用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”第一步应先假设( )
A.∠B≥90° B.∠B>90° C.∠B<90° D.AB≠AC
33.(2021·河北秦皇岛·七年级期中)下列命题中是假命题的是( )
A.对顶角相等 B.同旁内角互补 C.两点确定一条直线 D.垂线段最短
34.(2021·河北张家口·七年级期中)有下列命题,其中假命题有( )
①内错角相等.
②在同一平面内,垂直于同一条直线的两直线平行.
③相等的角是对顶角.
④经过直线外一点,有且只有一条直线与已知直线平行.
A.①② B.①③ C.②④ D.③④
35.(2021·河北唐山·八年级期中)下列命题的逆命题是真命题的是( )
A.若,则 B.同位角相等,两直线平行
C.对顶角相等 D.若,,则
36.(2021·河北张家口·七年级期中)下列命题中,是假命题的是( )
A.两点之间,线段最短 B.对顶角相等
C.直角的补角仍然是直角 D.同旁内角互补
37.(2021·河北唐山·七年级期中)如图,沿射线方向平移到(点E在线段上),如果,,那么平移距离为( )
A.3cm B.5cm C.8cm D.13cm
38.(2021·河北唐山·七年级期中)在下面的四幅图案中,能通过图案(1)平移得到的是( )
A. B. C. D.
39.(2021·河北沧州·七年级期中)四根火柴棒摆成如图所示的象形“口”字,平移此象形字火柴棒后,变成的象形文字正确的是( )
A. B. C. D.
40.(2021·河北唐山·八年级期中)如图,在10×6的网格中,每个小方格的边长都是1个单位,将△ABC平移到△DEF的位置,下面正确的平移步骤是( )
A.先把△ABC向左平移5个单位,再向下平移2个单位
B.先把△ABC向右平移5个单位,再向下平移2个单位
C.先把△ABC向左平移5个单位,再向上平移2个单位
D.先把△ABC向右平移5个单位,再向上平移2个单位
41.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,若图形经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
A.向右平移4格,再向下平移4格
B.向右平移6格,再向下平移5格
C.向右平移4格,再向下平移3格
D.向右平移5格,再向下平移3格
42.(2021·河北秦皇岛·七年级期中)如图,将△ABC沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42 B.96 C.84 D.48
43.(2021·河北秦皇岛·七年级期中) 某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是( )
A.甲种方案所用铁丝最长 B.乙种方案所用铁丝最长
C.丙种方案所用铁丝最长 D.三种方案所用铁丝一样长
二、填空题
44.(2021·河北张家口·七年级期中)如图,直线AB,CD相交于点O,OA平分∠EOC,∠EOD=120°,则∠BOD=__________°.
45.(2021·河北邯郸·七年级期中)如图,直线AB与CD相交于点O,,若,则=______°.
46.(2021·河北张家口·七年级期中)如图,已知相交于点,,,则的度数是__________.
47.(2021·河北邯郸·七年级期中)如图,直线AB、CD相交于点O,若,则等于______________.
48.(2021·河北唐山·七年级期中)如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB=_______.
49.(2021·河北唐山·七年级期中)一大门的栏杆如图所示,BA垂直地面AE于点A,CD平行于地面AE,则∠ABC+∠BCD=_____.
50.(2021·河北邢台·七年级期中)如图,已知,,所以点三点共线的理由__________.
51.(2021·河北张家口·七年级期中)如图,一个宽度相等的纸条按如图所示方法折叠一下,则________度.
52.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,直线,则__________.
53.(2021·河北·曲阳县教育和体育局教研室七年级期中)如图,直线,被直线所截,,.若,则等于___________.
54.(2021·河北秦皇岛·七年级期中)将一副三角板如图放置,∠ECD=∠BAC=90°,使点A在DE上,BC//DE,则∠ACE的度数为_______.
55.(2021·河北秦皇岛·七年级期中)将“平行于同一条直线的两条直线平行”改写成“如果……那么……”的形式为_________________________________________________.
56.(2021·河北·青龙满族自治县教师发展中心八年级期中)请写出“两直线平行,同位角相等”的逆命题:_____________________________.
57.(2021·河北唐山·八年级期中)命题“全等三角形的对应角相等”的逆命题是_____命题.(填“真”或“假”)
58.(2021·河北张家口·七年级期中)若∠A与∠B的两边分别平行,且∠A比∠B的3倍少40°,则∠B=_____度.
59.(2021·河北唐山·八年级期中)如图,将沿方向平移至处.若,则=___.
60.(2021·河北沧州·七年级期中)如图,在三角形ABC中,∠C=90°,AC+BC=31,AB=25,则内部五个小直角三角形周长的和为_______.
61.(2021·河北唐山·七年级期中)边长为4的等边与等边互相重合,将沿直线L向左平移m个单位长度,将向右也平移m个单位长度,若,则m=________;若C、E是线段BF的三等分点时,m=________.
62.(2021·河北唐山·七年级期中)某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯.已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面如图所示,则购买地毯至少需要___________元.
试卷第1页,共3页
参考答案:
1.C
【解析】
根据对顶角的定义,可得答案.
A、∠1与∠2有一条边在同一条直线上,另一条边不在同一条直线上,不是对顶角,故A选项错误;
B、∠1与∠2没有公共顶点,不是对顶角,故B选项错误;
C、∠1与∠2的两边互为反向延长线,是对顶角,故C选项正确;
D、∠1与∠2的两边不是互为反向延长线,不是对顶角,故D选项错误.
故选:C.
【点睛】
本题考查了对顶角,利用∠1的两边与∠2的两边互为反向延长线是解题的关键.
2.C
【解析】
试题分析::∵∠AOE=140°,∠AOE和∠2是邻补角,
∴∠2=180°-140°=40°,
∵∠1=∠2,∴∠BOD=2∠2=80°,
又∵∠BOD和∠AOC是对顶角
∴∠AOC=∠BOD=80°.
故选C.
考点:1.邻补角2.对顶角.
3.C
【解析】
根据垂线段最短即可得.
解:于点,
沿挖水沟,则水沟最短,理由是垂线段最短,
故选:C.
【点睛】
本题考查了垂线段最短,掌握理解垂线段最短是解题关键.
4.D
【解析】
根据垂线的定义求出∠3,然后利用对顶角相等和补角的定义解答.
解:∵CO⊥AB,∠1=56°,
∴∠3=90° ∠1=90° 56°=34°,
∴∠2=∠3=34°,
∴的补角等于146°,
故选:D.
【点睛】
本题考查了垂线的定义,对顶角相等的性质以及补角的定义,是基础题,掌握两个角的和为180°,则称这两个角互补,是解题的关键.
5.D
【解析】
根据点到直线的距离定义逐项判断即可.
解:A中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
B中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
C中的AD不垂直BC,所以线段AD的长不是点A到直线BC距离,故此选项错误;
D中的AD⊥BC,所以线段AD的长是点A到直线BC距离,故此选项正确,
故选:D.
【点睛】
本题考查点到直线的距离定义,熟知点到直线的距离定义是解答的关键.
6.C
【解析】
根据垂线的作法,用直角三角板的一条直角边与l重合,另一条直角边过点P后沿直角边画直线即可;
根据分析可得C的画法正确;
故答案选C.
【点睛】
本题主要考查了垂线的作法,准确理解是解题的关键.
7.D
【解析】
在同一平面内,过已知直线上的一点有且只有一条直线垂直于已知直线;但画已知直线的垂线,可以画无数条.
在同一平面内,画已知直线的垂线,可以画无数条;
故选:D.
【点睛】
此题主要考查在同一平面内,垂直于平行的特征,解题的关键是熟知垂直的定义.
8.D
【解析】
根据垂线段的性质解答即可.
解:小华同学应选择→路线,因为垂线段最短,
故选:D.
【点睛】
本题考查了垂线段的性质,解题的关键是掌握垂线段的性质.
9.A
【解析】
根据垂线段最短可得AD≥4,进而可得答案.
解:∵AC=4,AC⊥BC于点C,
∴,
故选:A.
【点睛】
本题主要考查了垂线段的性质,解题的关键是掌握垂线段最短.
10.C
【解析】
试题分析:根据题意画出图形即可.
解:根据题意可得图形,
故选C.
点评:此题主要考查了垂线,关键是掌握垂线的定义:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
11.D
【解析】
根据同旁内角的定义(两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角叫做同旁内角)即可得.
解:的同旁内角有,共5个,
故选:D.
【点睛】
本题考查了同旁内角,熟记定义是解题关键.
12.B
【解析】
根据同位角:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角可得答案.
解:图①中∠1与∠2是同位角,
图②中∠1与∠2不是同位角,
图③中∠1与∠2是同位角,
图④中∠1与∠2不是同位角,
故选:B.
【点睛】
此题主要考查了同位角,关键是掌握同位角的边构成“F“形.
13.C
【解析】
根据同位角的定义,进行分析求解即可得到答案.
解:如图所示
由AB、CD、EF组成的“三线八角”中同位角有四对;
射线GM和直线CD被直线EF所截,形成2对同位角;
射线GM和直线HN被直线EF所截,形成2对同位角;
射线HN和直线AB被直线EF所截,形成2对同位角.
则总共10对.
故选C.
【点睛】
本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.
14.C
【解析】
根据两条直线有一个交点的直线是相交线,没有交点的直线是平行线,可得答案.
在同一平面内,两条直线有一个交点,两条直线相交;在同一平面内,两条直线没有交点,两条直线平行,故C正确;
故选:C.
【点睛】
本题主要考查了同一平面内,两条直线的位置关系,注意垂直是相交的一种特殊情况,不能单独作为一类.
15.B
【解析】
根据平行线间的距离的定义,可得答案.
解:∵直线a∥b,CD⊥b,
∴直线a,b之间距离是线段CD的长度,
故选B.
【点睛】
本题考查了平行线间的距离,熟知平行线间的距离的定义是解题关键.
16.C
【解析】
根据平行线的判定逐项判断即可得.
A、由可得,则此项不符合题意;
B、由可得,则此项不符合题意;
C、由可得,则此项符合题意;
D、由不能判断,则此项不符题意;
故选:C.
【点睛】
本题考查了平行线的判定,熟练掌握平行线的判定方法是解题关键.
17.B
【解析】
根据平行线的判定逐项判断即可.
解:A、∵∠3=∠4,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意;
B、∵∠1=∠2,
∴AB∥CD,此选项符合题意;
C、∵,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意;
D、∵,
∴AC∥BD,不能判断AB∥CD,此选项不符合题意,
故选:B.
【点睛】
本题考查平行线的判定,熟练掌握平行线的判定是解答的关键.
18.C
【解析】
根据平行线的判定定理判断即可.
∵,∴a∥b,∴A选项不符合题意;
∵,∴a∥b,∴B选项不符合题意;
∵,∴a∥b,∴D选项不符合题意;
∵,无法判断a∥b,∴C选项符合题意;
故选C.
【点睛】
本题考查了平行线的判定定理,熟记平行线判定定理是解题的关键.
19.B
【解析】
根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意得:两次拐的方向不相同,但角度相等.
解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
因此,第一次与第二次拐的方向不相同,角度要相同,
故只有B选项符合,
故选B.
【点睛】
此题主要考查了平行线的性质,注意要想两次拐弯后,仍在原来的方向上平行前进,则拐的方向应相反,角度应相等.
20.C
【解析】
根据小明小刚的描述,两种操作的结果都能使∠1=60°,可得结果.
解:根据小明的操作,把木条绕点M逆时针旋转10°,则,根据同位角相等,两直线平行,故;根据小刚的操作,如解图,把木条绕点M顺时针旋转170°,则,即.同理可得,.因此,小明和小刚的操作都正确.
故选C.
【点睛】
本题考查了平行线的判定,同位角相等,两直线平行.
错因分析 容易题.失分的原因是:1.没有掌握平行线的判定,其中同位角或内错角相等、同旁内角互补,两直线平行.2.没有掌握旋转的基本性质.
21.D
【解析】
如图(见解析),先根据平行线的性质可得,再根据平角的定义即可得.
解:如图,由题意得:,
,
又,
,
,
故选:D.
【点睛】
本题考查了平行线的性质、平角的定义等知识点,熟练掌握平行线的性质是解题关键.
22.A
【解析】
根据平行线的判定与性质逐一进行判断推理即可.
解:∵AB//CD,∴∠B=∠DCE(两直线平行,同位角相等),故A正确;
∵∠1=∠2,∴AB//CD(内错角相等,两直线平行),故B错误;
∵AD//BC,∴∠3=∠4(两直线平行,内错角相等),故C错误;
∵∠B+∠BCD=180°,∴AB//CD(同旁内角互补,两直线平行),故D错误.
故选:A.
【点晴】
考查了平行线的判定与性质,解题关键是仔细观察图形灵活运用平行线的判定与性质进行推理.
23.C
【解析】
根据两直线平行,同位角相等可得∠3=∠2,再根据邻补角的定义解答.
如图,
∵a∥b,∠2=45°,
∴∠3=∠2=45°,
∴∠1=180° ∠3=135°,
故选:C.
【点睛】
本题考查了平行线的性质,解题的关键是掌握平行线性质定理
定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.
定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.
定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.
24.A
【解析】
根据三角板自带角的度数以及平行的性质可得.
解:∵AB∥EF,
∴∠ADE=∠DAB=∠DAC+∠CAB=45°+30°=75°,
又∵∠ADC=90°,
∴∠CDF=180°-∠ADC-∠ADE=15°
故选 A.
【点睛】
本题考查了三角板的认识和平行线的性质,解题的关键在于能够熟练掌握相关知识进行求解.
25.D
【解析】
根据题意易得,然后根据平角的定义可得,进而根据平行线的性质可求解.
解:由题意得:,
∵,
∴,
∵,
∴;
故选D.
【点睛】
本题主要考查平行线的性质,熟练掌握平行线的性质是解题的关键.
26.C
【解析】
由AB∥CD得∠1=∠2,∠B=∠3,根据平行线的推论得EC⊥CD,再由余角的性质得∠1与∠ACE、∠B、∠3三个角互余,进而即可得到答案.
解:如图所示:
∵AB∥CD,
∴∠1=∠2,
又∵EC⊥AB,
∴EC⊥CD,
∴∠2+∠ACE=90°,
∴∠1+∠ACE=90°,
∴∠1与∠ACE互余;
又∵AC⊥BC,
∴∠ACB=90°,
∴∠CAB+∠B=90°,
又∵∠1=∠CAB,
∴∠1+∠B=90°,
∴∠1与∠B互余;
又∵AB∥CD,
∴∠B=∠3,
∴∠1+∠3=90°,
∴∠1与∠3互余,
综合所述,图中与∠1互余的角的个数为3,
故选:C.
【点睛】
本题综合考查了平行线的性质,垂直的定义,对顶角的性质,余角的性质等相关知识点,重点掌握平行线的性质,难点是找余角的个数时不重不漏.
27.C
【解析】
先求出,再根据平行线的性质即可得.
解:,
,
,
,
故选:C.
【点睛】
本题考查了平行线的性质等知识点,熟练掌握平行线的性质是解题关键.
28.D
【解析】
根据平行线的性质、对顶角相等即可得.
A、当两个角的两边互相平行时,一定成立,则此项不符题意;
B、如图,当时,一定成立,则此项不符题意;
C、如图,,当时,一定成立,则此项不符题意;
D、由对顶角相等得:一定成立,则此项符合题意;
故选:D.
【点睛】
本题考查了平行线的性质、对顶角相等,熟练掌握对顶角相等是解题关键.
29.C
【解析】
试题分析:先根据两角互余的性质求出∠3的度数,再由平行线的性质即可得出结论.∵∠1+∠3=90°,
∠1=30°,∴∠3=60°. ∵直尺的两边互相平行, ∴∠2=∠3=60°.
考点:平行线的性质
30.B
【解析】
(1)根据平行线的性质进行判断即可;
(2)根据对顶角的概念进行判断即可;
(3)根据平行公理的推论进行判断即可;
(4)根据垂线段的概念进行判断即可.
解:(1)只有两条平行线被第三条直线所截,同位角才相等,故此说法错误;
(2)相等的角不一定是对顶角,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,故此说法错误;
(3)假设它与另一条平行,根据平行于同一直线的两直线平行可得它与第一条也平行,这与已知条件相矛盾,故平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交,此说法正确;
(4)从直线外一点到这条直线的垂线段的长度,叫做这点到直线的距离,故此说法错误.
故正确的说法有1个.
故选B.
【点睛】
本题主要考查了平行线的性质,对顶角的概念,平行公理的推论及垂线段的概念,熟记这些定理及概念是解决此题的关键.
31.B
【解析】
判断事物的语句叫命题,根据命题的定义逐一进行判断即可得到答案.
解:A、美丽的天空,是描叙性语言,它不是命题,所以A选项不符合题意;
B、相等的角是对顶角是命题,所以B选项符合题意;
C、作线段AB=CD,是描叙性语言,它不是命题,所以C选项不符合题意;
D、你喜欢运动吗?,是疑问句,没有对事物作出判断,它不是命题,所以D选项不符合题意.
故选:B.
【点睛】
本题考查了命题的定义,掌握根据命题的定义进行命题的判断是解题的关键.
32.A
【解析】
反证法的第一步就是假设命题反面成立
用反证法证明命题:“已知△ABC,AB=AC,求证:∠B<90°.”,第一步应先假设∠B≥90°;
故选:A
【点睛】
本题考查反正法的步骤:1、假设命题反面成立;2、从假设出发,经过推理得出和反面命题矛盾,或者与定义、公理、定理矛盾;3、得出假设命题不成立是错误的,即所求证命题成立
33.B
【解析】
根据平行线的性质、对顶角的性质、直线的概念、垂线段的性质定理判断.
A、对顶角相等,本选项说法是真命题;
B、两直线平行,同旁内角才互补,故本选项说法是假命题;
C、两点确定一条直线,本选项说法是真命题;
D、垂线段最短,本选项说法是真命题;
故选:B.
【点睛】
本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
34.B
【解析】
利用平行线的性质、对顶角的定义及平行公理分别判断后即可确定正确的选项.
①两直线平行,内错角相等,故原命题错误,是假命题,符合题意.
②在同一平面内,垂直于同一条直线的两直线平行,正确,是真命题,不符合题意.
③相等的角不一定是对顶角,故原命题错误,是假命题,符合题意.
④经过直线外一点,有且只有一条直线与已知直线平行,正确,是真命题,不符合题意.
故选:B.
【点睛】
本题考查命题与定理的知识,解题的关键是了解平行线的性质、对顶角的定义以及平行公理.
35.B
【解析】
分别写出原命题的逆命题,然后判断真假即可.
解:A、若,则的逆命题是若,则,逆命题是假命题,不符合题意;
B、同位角相等,两直线平行的逆命题是两直线平行,同位角相等,逆命题是真命题,符合题意;
C、对顶角相等的逆命题是相等的角是对顶角,逆命题是假命题,不符合题意;
D、若,,则的逆命题是若,则,,逆命题是假命题,不符合题意;
故选:B.
【点睛】
本题考查了命题与定理的知识,解题的关键是正确的写出一个命题的逆命题,难度不大.
36.D
【解析】
根据线段、对顶角、补角、平行线的性质判断即可.
解:A、两点之间,线段最短,是真命题;
B、对顶角相等,是真命题;
C、直角的补角仍然是直角,是真命题;
D、如果两直线不平行,同旁内角不互补,所以同旁内角互补,是假命题;
故选:D.
【点睛】
此题考查了命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
37.A
【解析】
观察图象,发现平移前后,B、E对应,C、F对应,根据平移的性质,易得平移的距离=BE,进而可得答案.
解:根据平移的性质,
易得平移的距离=BE=8-5=3cm,
故选:A.
【点睛】
本题考查平移的性质,经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等,本题关键要找到平移的对应点.
38.C
【解析】
平移前后形状与大小没有改变,并且对应点的连线平行且相等的图形即可.
解:A、对应点的连线相交,不能通过平移得到,不符合题意;
B、对应点的连线相交,不能通过平移得到,不符合题意;
C、可通过平移得到,符合题意;
D、对应点的连线相交,不能通过平移得到,不符合题意;
故选:C.
【点睛】
本题考查了平移变换,解题的关键是熟练掌握平移变换的性质,属于中考常考题型.
39.C
【解析】
根据火柴头的方向、平移的定义即可得.
解:此象形字火柴棒中,有两根火柴头朝向左,一根火柴头朝向上,一根火柴头朝向下,
因为平移不改变火柴头的朝向,
所以观察四个选项可知,只有选项C符合,
故选:C.
【点睛】
本题考查了平移,掌握理解平移的概念是解题关键.
40.A
【解析】
解:根据网格结构,观察点对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,
所以,平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选A.
41.A
【解析】
根据图形A与下方图形中空白部分的位置解答即可.
解:由图可知,正确的平移方式是向右平移4格,再向下平移4格.
故选A.
【点睛】
本题考查平移特征,掌握平移特征是解题关键.
42.D
【解析】
根据平移的性质得出BE=6,DE=AB=10,则OE=6,则阴影部分面积=S四边形ODFC=S梯形ABEO,根据梯形的面积公式即可求解。
由平移的性质知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∴S四边形ODFC=S梯形ABEO=(AB+OE) BE=×(10+6)×6=48.
故选D.
【点睛】
本题考查平移的性质,平移前后两个图形大小,形状完全相同,图形上的每个点都平移了相同的距离,对应点之间的距离就是平移的距离.
43.D
【解析】
试题分析:
解:由图形可得出:甲所用铁丝的长度为:2a+2b,
乙所用铁丝的长度为:2a+2b,
丙所用铁丝的长度为:2a+2b,
故三种方案所用铁丝一样长.
故选D.
考点:生活中的平移现象
44.30
【解析】
先利用补角的定义求出∠EOC=60°,再根据角平分线的性质计算.
解:∵∠EOD=120°,
∴∠EOC=60°(邻补角定义).
∵OA平分∠EOC,
∴∠AOC=∠EOC=30°(角平分线定义),
∴∠BOD=30°(对顶角相等).
故答案为:30.
【点睛】
本题考查由角平分线的定义,结合补角的性质,易求该角的度数.
45.35°
【解析】
先根据垂直的定义和角的和差求出∠BOD的度数,再根据对顶角相等的性质解答即可.
解:∵,
∴∠BOM=90°,
∵,
∴∠BOD=90°-55°=35°,
∴∠AOC=∠BOD=35°,
故答案为:35.
【点睛】
本题考查了垂直的定义、对顶角的性质和角的和差计算,属于基础题目,熟练掌握基本知识是解题的关键.
46.
【解析】
依据、、相交于点,,,即可得到,再根据对顶角相等,即可得出.
解:、、相交于点,,,
,
又与是对顶角,
,
故答案为:.
【点睛】
本题考查了对顶角相等的性质,平角的定义,解题的关键是准确识图.
47.130°
【解析】
根据对顶角相等可得∠1=∠2,再求出∠1,然后根据邻补角的定义列式计算即可得.
解:由对顶角相等可得,∠1=∠2,
∵∠1+∠2=100°,
∴∠1=50°,
∴∠BOC=180° ∠1=180° 50°=130°
故答案为:130°
【点睛】
本题考查对顶角、邻补角,关键是熟记对顶角的性质和邻补角的定义.
48.128°##128度
【解析】
根据垂直的定义得出∠AOE=90°,最后根据∠COB=∠AOD=∠AOE +∠EOD进行求解.
∵OE⊥AB,∠EOD=38°,
∴∠AOE=90°,
∴∠COB=∠AOD=∠AOE +∠EOD=90°+38°=128°,
故答案为:128°.
【点睛】
本题考查垂直的定义,对顶角的性质,熟练掌握对顶角相等是解题的关键.
49.270°
【解析】
过B作BF∥AE,则CD∥BF∥AE.根据平行线的性质即可求解.
过B作BF∥AE,
∵CD∥ AE,
则CD∥BF∥AE,
∴∠BCD+∠1=180°,
又∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∴∠ABC+∠BCD=90°+180°=270°.
故答案为:270.
【点睛】
本题主要考查了平行线的性质,两直线平行,同旁内角互补.正确作出辅助线是解题的关键.
50.平行公理的推论
【解析】
根据平行公理的推论即可得.
平行公理的推论:平行于同一条直线的两条直线互相平行
则点三点共线
故答案为:平行公理的推论.
【点睛】
本题考查了平行公理的推论,熟记平行公理的推论是解题关键.
51.65
【解析】
根据两直线平行内错角相等,以及折叠关系列出方程求解则可.
解:如图,由题意可知,
AB∥CD,
∴∠1+∠2=130°,
由折叠可知,∠1=∠2,
∴2∠1=130°,
解得∠1=65°.
故答案为:65.
【点睛】
本题考查了平行线的性质和折叠的知识,题目比较灵活,难度一般.
52.
【解析】
过点C作CD∥a,则CD∥b,利用平行线的性质求解即可
如图,过点C作CD∥a,
∵直线,
∴CD∥b,
∴∠ACD=30°,∠DCB=50°,
∴∠ACB=∠ACD+∠DCB =30°+50°=80°,
故答案为:80°.
【点睛】
本题考查了平行线的判定,平行线的性质,角的和,熟练构造平行线辅助线,活用平行线的判定与性质是解题的关键.
53.
【解析】
由a∥b得,,由∠3+∠1+∠2=180°及已知,可求得∠1的度数,从而可得结果.
∵a∥b
∴
∵∠3+∠1+∠2=180°,,
∴
∴
故答案为:
【点睛】
本题考查了平行线的性质.
54.15°
【解析】
根据两直线平行,内错角相等求出∠BCE=∠E=30°,然后求出∠ACE的度数.
∵BC∥DE,
∴∠BCE=∠E=30°,
∴∠ACE=∠ACB ∠BCE=45° 30°=15°,
故答案为:15°.
【点睛】
本题主要考查了平行线的性质,关键是掌握两直线平行,内错角相等.
55.如果两条直线平行于同一条直线,那么这两条直线平行
【解析】
命题由题设和结论两部分组成,通常写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.
命题可以改写为:如果两条直线平行于同一条直线,那么这两条直线平行.
故答案为:如果两条直线平行于同一条直线,那么这两条直线平行
【点睛】
任何一个命题都可以写成“如果…那么…”的形式.“如果”后面接题设,“那么”后面接结论.在改写过程中,不能简单地把题设部分、结论部分分别塞在“如果”、“那么”后面,要适当增减词语,保证句子通顺而不改变原意.
56.如果同位角相等,那么两直线平行
【解析】
命题是由题设和结论两部分组成的,把原命题的题设作结论,原命题的结论作题设,这样就将原命题变成了它的逆命题.
解:原命题是:两直线平行,同位角相等.
改成如果…那么…的形式为:如果两直线平行,那么同位角相等.
∴逆命题为:如果同位角相等,那么两直线平行,
故答案为:如果同位角相等,那么两直线平行.
【点睛】
本题是一道命题与定理的概念试题,考查了命题的组成,原命题与逆命题的关系.
57.假
【解析】
首先分清题设是:两个三角形全等,结论是:对应角相等,把题设与结论互换即可得到逆命题,然后判断正误即可.
解:“全等三角形的对应角相等”的题设是:两个三角形全等,结论是:对应角相等,因而逆命题是:对应角相等的三角形全等.是一个假命题.
故答案为:假.
【点睛】
本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.
58.55或20
【解析】
根据平行线性质得出∠A+∠B=180°①,∠A=∠B②,求出∠A=3∠B﹣40°③,把③分别代入①②求出即可.
解:∵∠A与∠B的两边分别平行,
∴∠A+∠B=180°①,∠A=∠B②,
∵∠A比∠B的3倍少40°,
∴∠A=3∠B﹣40°③,
把③代入①得:3∠B﹣40°+∠B=180°,
∠B=55°,
把③代入②得:3∠B﹣40°=∠B,
∠B=20°,
故答案为:55或20.
【点睛】
本题考查平行线的性质,解题的关键是掌握由∠A和∠B的两边分别平行,即可得∠A =∠B或∠A+∠B=180° ,注意分类讨论思想的应用.
59.3
【解析】
根据平移的性质得到,再用得到的长,从而得到的长.
解:∵沿方向平移至处,
∴,
∵,
∴,
∴,
∴,
故答案为3.
【点睛】
本题考查了平移的性质,解题的关键是掌握把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.
60.56
【解析】
先根据平移的性质可得内部五个小直角三角形的直角边的和等于,再根据三角形的周长公式即可得.
解:由题意得:内部五个小直角三角形的直角边的和等于,
则内部五个小直角三角形周长的和为,
故答案为:56.
【点睛】
本题考查了平移的性质等知识点,熟练掌握平移的性质是解题关键.
61. 5 1或4
【解析】
由平移的性质可知,可得m的值;若C、E是线段BF的三等分点时,
将沿直线L向左平移m个单位长度,将向右也平移m个单位长度,两个三角形完全不重叠时,由平移的性质可知,可得m的值;两个三角形部分重叠时,,,可得m值.
解:由平移的性质可知;
如图,两个三角形完全不重叠时,因为C、E是线段BF的三等分点,所以,由平移的性质可知,所以;
如图,两个三角形部分重叠时,因为C、E是线段BF的三等分点,,
综上所述,m的值为1或4.
故答案为(1)5 (2) 1或4
【点睛】
本题考查了平移的性质,熟练掌握平移的距离即为对应点所连线段的长度这一性质是解题的关键.
62.512
【解析】
根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.
解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为5.5米,2.5米,
∴地毯的长度为2.5+5.5=8米,地毯的面积为8×2=16平方米,
∴买地毯至少需要16×32=512元.
故答案为:512
【点睛】
本题考查了平移的应用,解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.
答案第1页,共2页
同课章节目录
