第8章整式的乘法解答题练习(河北地区专用)2021-2022学年下学期河北省各地冀教版七年级数学期中复习(Word版含解析)
文档属性
| 名称 | 第8章整式的乘法解答题练习(河北地区专用)2021-2022学年下学期河北省各地冀教版七年级数学期中复习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 725.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览


文档简介
第8章 整式的乘法解答题
1.(2021·河北唐山·七年级期中)计算:
(1)2-2+(3721﹣4568)0
(2)(-x2)3+(-3x2)2 x2
2.(2021·河北保定·七年级期中)计算或化简:
(1);
(2);
(3).
3.(2021·河北保定·七年级期中)计算:
(1) (2)
(3) (4)
(5)先化简,再求值,其中,.
4.(2021·河北保定·七年级期中)先化简,再求值:,其中,.
5.(2021·河北唐山·七年级期中)计算:(1);
(2).
6.(2021·河北邯郸·七年级期中)运用整式乘法公式计算
(1)899901
(2)-124122
7.(2021·河北邯郸·七年级期中)(1)
(2)
8.(2021·河北秦皇岛·七年级期中)计算:
(1)(2a+5b)(2a-5b)-(a-3b)2.
(2)利用乘法公式进行简便计算:
9.(2021·河北石家庄·七年级期中)(1)
(2)
(3)解方程组
10.(2021·河北·石家庄市栾城区教育局教研室七年级期中)(1)解方程组.
(2)计算.
11.(2021·河北秦皇岛·七年级期中)计算
(1)
(2)
(3)求的值,其中x=2.
12.(2021·河北·曲阳县教育和体育局教研室七年级期中)计算:(1);
(2);
(3)先化简,再求值:,其中.
13.(2021·河北·石家庄市栾城区教育局教研室七年级期中)先化简,再求值:,其中.
14.(2021·河北邢台·七年级期中)化简:.
15.(2021·河北邯郸·七年级期中)计算:
(1)
(2)
16.(2021·河北石家庄·七年级期中)已知x2﹣3x=1,求代数式(x﹣1)(3x+1)﹣(x+2)2﹣4的值.
17.(2021·河北衡水·七年级期中)已知,求代数式的值.
18.(2021·河北唐山·七年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
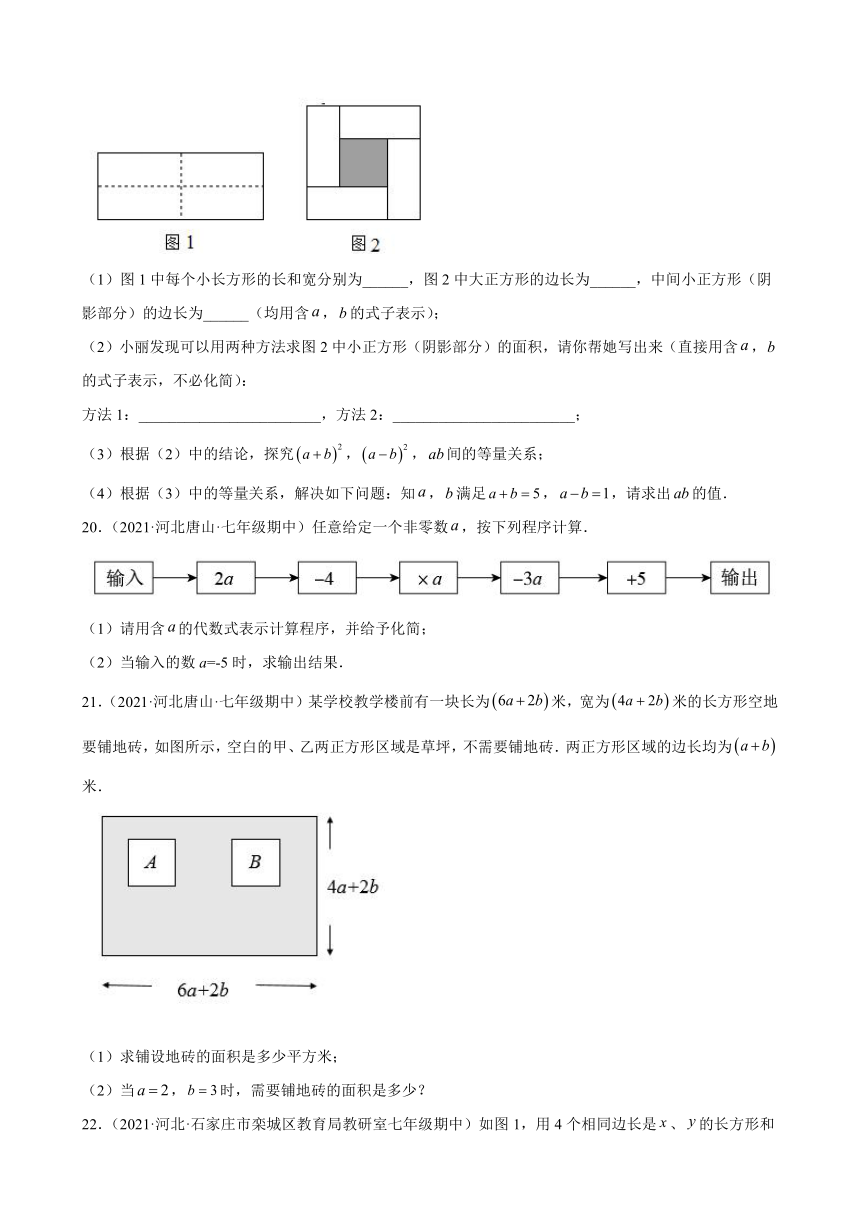
19.(2021·河北保定·七年级期中)学完整式的乘法公式后,爱思考的小丽同学为了探究公式之间的联系,她把一个长为,宽为的长方形沿图1中虚线用剪刀平均分成四个小长方形,然后拼成一个大正方形(如图2).请你根据小丽的操作回答下列问题:
(1)图1中每个小长方形的长和宽分别为______,图2中大正方形的边长为______,中间小正方形(阴影部分)的边长为______(均用含,的式子表示);
(2)小丽发现可以用两种方法求图2中小正方形(阴影部分)的面积,请你帮她写出来(直接用含,的式子表示,不必化简):
方法1:________________________,方法2:________________________;
(3)根据(2)中的结论,探究,,间的等量关系;
(4)根据(3)中的等量关系,解决如下问题:知,满足,,请求出的值.
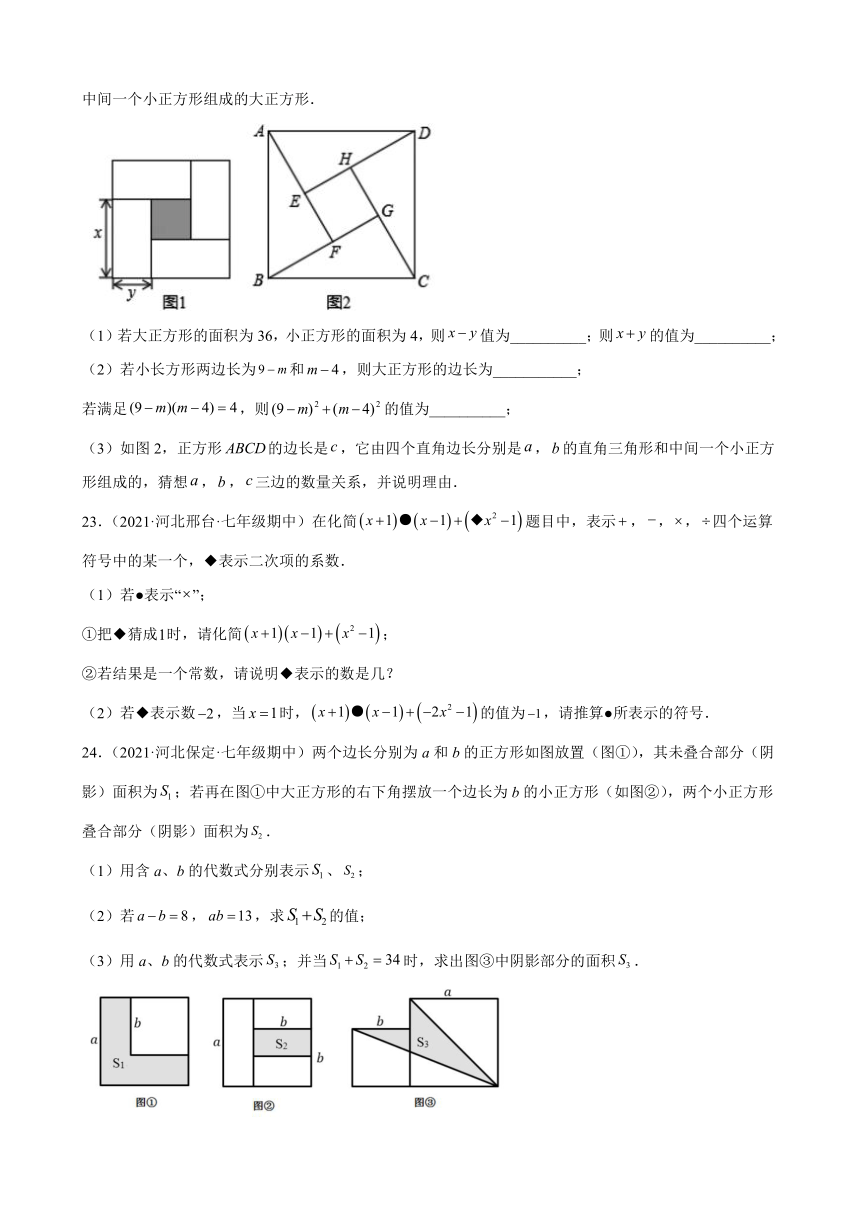
20.(2021·河北唐山·七年级期中)任意给定一个非零数,按下列程序计算.
(1)请用含的代数式表示计算程序,并给予化简;
(2)当输入的数a=-5时,求输出结果.
21.(2021·河北唐山·七年级期中)某学校教学楼前有一块长为米,宽为米的长方形空地要铺地砖,如图所示,空白的甲、乙两正方形区域是草坪,不需要铺地砖.两正方形区域的边长均为米.
(1)求铺设地砖的面积是多少平方米;
(2)当,时,需要铺地砖的面积是多少?
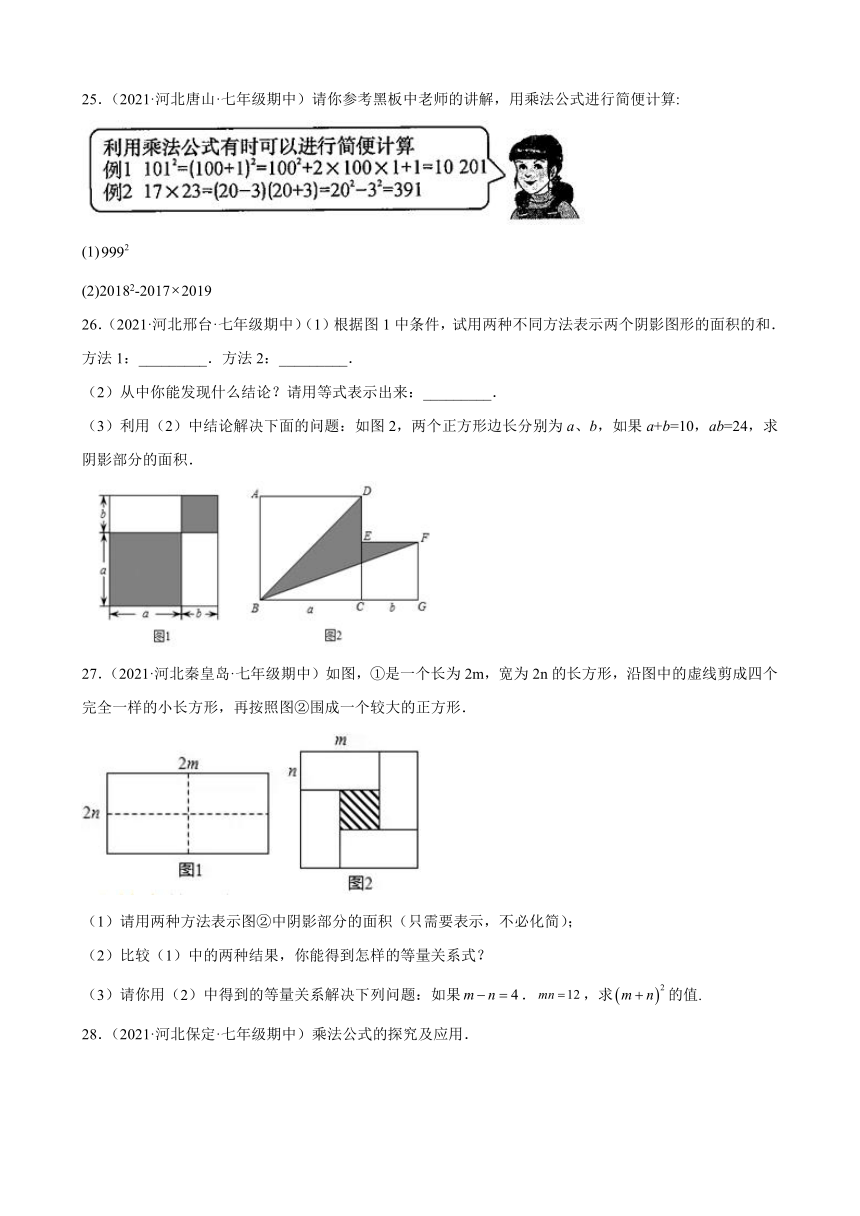
22.(2021·河北·石家庄市栾城区教育局教研室七年级期中)如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为__________;则的值为__________;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
23.(2021·河北邢台·七年级期中)在化简题目中,表示,,,四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“”;
①把◆猜成时,请化简;
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数,当时,的值为,请推算●所表示的符号.
24.(2021·河北保定·七年级期中)两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为;若再在图①中大正方形的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为.
(1)用含a、b的代数式分别表示、;
(2)若,,求的值;
(3)用a、b的代数式表示;并当时,求出图③中阴影部分的面积.
25.(2021·河北唐山·七年级期中)请你参考黑板中老师的讲解,用乘法公式进行简便计算:
(1)
(2)20182-20172019
26.(2021·河北邢台·七年级期中)(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:_________.方法2:_________.
(2)从中你能发现什么结论?请用等式表示出来:_________.
(3)利用(2)中结论解决下面的问题:如图2,两个正方形边长分别为a、b,如果a+b=10,ab=24,求阴影部分的面积.
27.(2021·河北秦皇岛·七年级期中)如图,①是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全一样的小长方形,再按照图②围成一个较大的正方形.
(1)请用两种方法表示图②中阴影部分的面积(只需要表示,不必化简);
(2)比较(1)中的两种结果,你能得到怎样的等量关系式?
(3)请你用(2)中得到的等量关系解决下列问题:如果.,求的值.
28.(2021·河北保定·七年级期中)乘法公式的探究及应用.
(1)如图 1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式)
(3)比较图 1,图 2 的阴影部分面积,可以得到乘法公式 (用式子表达)
(4)应用所得的公式计算:(1﹣ )(1﹣)(1﹣)…(1﹣)(1﹣)
29.(2021·河北唐山·七年级期中)一个长方形的长为2xcm,宽比长少4cm,若将长方形的长和宽都扩大3cm.
(1)求扩大后长方形的面积是多少?(用含x的代数式表示)
(2)若,求扩大后长方形的面积是多少?
30.(2021·河北邯郸·七年级期中)如图,在图(1)中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图(2)的方式拼成一个长方形
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.
31.(2021·河北唐山·七年级期中)欢欢与乐乐两人共同计算,欢欢抄错为,得到的结果为;乐乐抄错为,得到的结果为.
式子中的a、b的值各是多少?
请计算出原题的正确答案.
32.(2021·河北·曲阳县教育和体育局教研室七年级期中)电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段 第二时段
完成列数 2 5
分数 634 898
操作次数 66 102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
33.(2021·河北衡水·七年级期中)发现 任意五个连续整数的平方和是5的倍数.
验证 (1)(–1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
试卷第1页,共3页
参考答案:
1.(1);(2)8x6
【解析】
(1)先算负整数指数幂和零指数幂,再算加法,即可求解;
(2)先算幂的乘方和积的乘方,进而即可求解.
【详解】
解:(1)原式=+1
=;
(2)原式=-x6+9x4 x2
=-x6+9x6
=8x6.
【点睛】
本题主要考查实数的混合运算以及整式的运算,掌握负整数指数幂和零指数幂的性质以及幂的乘方和积的乘方法则,是解题的关键.
2.(1)-4;(2);(3)
【解析】
(1)根据负指数幂及零次幂可直接进行求解;
(2)根据积的乘方、单项式除以单项式及整式的乘法可直接进行求解;
(3)根据多项式乘多项式可进行求解.
【详解】
解:(1)原式=;
(2)原式=;
(3)原式=.
【点睛】
本题主要考查负指数幂、零次幂、分式的运算、多项式乘多项式及单项式除单项式,熟练掌握负指数幂、零次幂、分式的运算、多项式乘多项式及单项式除单项式是解题的关键.
3.(1);(2);(3);(4);(5),
【解析】
(1)根据平方差公式即可求解;
(2)根据单项式的除法法则即可求解;
(3)先算零指数幂和负整数指数幂,再算乘法,即可求解;
(4)先算单项式的乘除法,再合并同类项即可求解;
(5)先化简括号内的整式,再算整式的除法,最后代入求值,即可.
【详解】
解:(1)原式=
=;
(2)原式=
=;
(3)原式=
=;
(4)原式=
=
=;
(5)原式=
=
=
=,
当,时,原式=.
【点睛】
本题主要考查实数的混合运算,整式的化简求值,零指数幂和负整数指数幂的性质,熟练掌握整式的混合运算法则和乘法公式,是解题的关键.
4.,0
【解析】
先对整式进行化简,然后再把x、y的值代入求解即可.
【详解】
解:原式=
=
=,
把,代入得:
原式=.
【点睛】
本题主要考查整式的化简求值,熟练掌握整式的运算是解题的关键.
5.(1);(2).
【解析】
(1)根据积的乘方、单项式乘单项式和同底数幂的除法可以解答本题;
(2)根据完全平方公式、平方差公式可以解答本题.
【详解】
解:(1)
;
(2)
.
【点睛】
本题考查了整式的混合运算,涉及到积的乘方、同底数幂的除法、乘法公式等,解答本题的关键是明确它们各自的计算方法.
6.(1)809999;(2)1
【解析】
(1)利用平方差公式求解即可;
(2)先利用平方差公式计算,进而即可求解.
【详解】
(1)899901
=(900-1)(900+1)
=-1
=810000-1
=809999;
(2)-124122
=-(123+1)(123-1)
=-
=1.
【点睛】
本题考查了运用整式乘法公式计算,掌握整式的乘法公式是解题的关键.
7.(1);(2)
【解析】
(1)根据整式的乘法对式子进行运算即可;
(2)根据整式的除法对式子进行运算即可.
【详解】
(1)解:
(2)解:
【点睛】
此题主要考查了整式的乘除运算,熟练掌握整式乘除的运算法则是解题的关键.
8.(1)3a2+6ab-34b2;(2)-1
【解析】
(1)根据平方差公式和完全平方公式展开化简可以解答本题;
(2)根据平方差公式可以解答本题;
【详解】
(1)(2a+5b)(2a-5b)-(a-3b)2
=4a2-25b2-a2+6ab-9b2
=3a2+6ab-34b2
(2)
=
=
=-1.
【点睛】
本题考查整式的混合运算,解题的关键是明确平方差和完全平方公式的计算方法.
9.(1)2;(2)-a3b6 ;(3)
【解析】
(1)先计算乘方,负指数幂,零指数幂,然后再计算加减即可;
(2)根据积的乘方法则计算,在算单项式与单项式相乘法则计算,最后合并同类项即可;
(3)先标号,由①得x=8-3y③,利用代入消元法解方程组即可.
【详解】
(1)解:,
=-1+4-1,
=2;
(2)解:,
=8a3b6-9ab2×a2b4,
=8a3b6-9a3b6,
=-a3b6;
(3)解:,
由 ①得x=8-3y③,
把③代入②得:,
解得:,
把代入③得:.
∴原方程组的解是.
【点睛】
本题考查实数运算,乘方,负指数幂,零指数幂,整式的幂指数混合运算,解得乘方,单项式乘单项式,合并同类项,二元一次方程组解法,掌握实数运算,乘方,负指数幂,零指数幂,整式的幂指数混合运算,解得乘方,单项式乘单项式,合并同类项,二元一次方程组解法是解题关键.
10.(1);(2)
【解析】
(1)利用求解二元一次方程组的代入消元法求解即可;
(2)利用积的乘方等于乘方的积以及幂的乘方进行化简,然后合并求值即可.
【详解】
解:(1),
把代入②,
得:,
解得:,
把代入①得:,
故原方程组的解为:.
(2)解:原式
.
【点睛】
本题主要考查解二元一次方程组、积的乘方以及幂的乘方的运算,熟练掌握方法以及积的乘方的运用是解题关键.
11.(1) (2) (3) ,-14;
【解析】
(1)先将原式运用平方差公式进行展开,继而利用提公因式法进行计算即可;
(2)利用单项乘以多项式的运算法则进行计算即可;
(3)先将原式进行化简,再将x的值代入进行求解即可;
【详解】
(1)原式=
(2)原式=
(3)原式=
,
将 代入得:
【点睛】
本题考查了因式分解、单项式乘以多项式、整式的混合运算、多项式乘以多项式,正确掌握运算法则是解题的关键;
12.(1);(2);(3),-8
【解析】
(1)按照单项式的乘法法则计算即可;
(2)运用完全平方公式,平方差公式展开化简即可;
(3)运用乘法公式化简,后代入求值
【详解】
(1)
=
=;
(2)
=
=
(3)解:原式
.
当时,原式.
【点睛】
本题考查了整式的乘法,完全平方公式,平方差公式,化简求值,熟练运用整式的乘法法则,完全平方公式,平方差公式进行化简是解题的关键.
13.
【解析】
先根据完全平方公式和平方差公式进行化简,再将代入即可
【详解】
解:
当时,原式=6+10=16.
【点睛】
本题考查了整式的化简求值,熟练掌握运算法则和计算公式是解题的关键
14.
【解析】
直接利用同底数幂的乘法,除法,积的乘方,幂的乘方计算化简即可.
【详解】
解:原式=
=
【点睛】
本题主要考查整式的混合运算,熟练掌握同底数幂的乘除法,幂的乘方,积的乘方的运算法则是解题的关键.
15.(1)-4y-2;(2)-4mn
【解析】
(1)根据多项式的乘法法则展开后再合并同类项即可得到解答;
(2)根据平方差公式和完全平方公式展开后再合并同类项即可得到解答.
【详解】
(1)解:原式=(y3+2y2+y-2y2-4y-2)-(y3+y)
=y3+2y2+y- 2y2-4y-2-y3-y
=-4y-2
(2)原式=(m2-4n2)-(m2+4mn+4n2)+8n2
=m2-4n2-m2-4mn- 4n2+8n2
=-4mn
【点睛】
本题考查多项式的乘法,灵活运用多项式乘法法则和乘法公式计算是解题关键.
16.﹣7.
【解析】
原式利用整式的乘法公式和完全平方公式展开后化简,再把x2﹣3x=1整体代入求得数值即可.
【详解】
解:原式=3x2﹣2x﹣1﹣(x2+4x+4)﹣4
=3x2﹣2x﹣1﹣x2﹣4x﹣4﹣4
=2x2﹣6x﹣9.
∵x2﹣3x=1.
∴原式=2(x2﹣3x)﹣9=2﹣9=﹣7.
【点睛】
本题考查了整式的化简求值,属于基本题型,熟练掌握整式的混合运算法则是解题的关键.
17.12
【解析】
将代数式应用完全平方公式和平方差公式展开后合并同类项,将整体代入求值.
【详解】
解:∵,∴.
∴
.
18.(1)>;(2)<;(3)-4
【解析】
(1)根据同指数的幂底数越大幂越大,可得答案;
(2)根据幂的乘方,可得指数相同的幂,根据底数越大幂越大,可得答案;
(3)先根据积的乘方逆运算进行运算,再进行减法运算即可得出答案.
【详解】
解:(1)∵5>4,
∴>,
故答案为:>;
(2)∵233=(23)11=811,322=(32)11=911,
又∵8<9,
∴<.
(3)
【点睛】
本题考查了幂的乘方以及积的乘方,利用同指数的幂底数越大幂越大是解题关键.
19.(1)a、b,a+b,a-b;(2),;(3);(4)6
【解析】
(1)由“一个长为,宽为的长方形沿图1中虚线用剪刀平均分成四个小长方形”可得每个长方形的长和宽,然后根据图形可求解问题;
(2)根据图形及割补法可进行求解问题;
(3)由(2)可直接进行求解;
(4)由,可得,,然后根据(3)的关系式可进行求解.
【详解】
解:(1)由题意得:
图1中每个小长方形的长和宽分别为a、b,图2中大正方形的边长为a+b,中间小正方形(阴影部分)的边长为a-b;
故答案为a、b,a+b,a-b;
(2)方法1:利用大正方形的面积减去四个小长方形的面积=小正方形的面积,即为;
方法2:由(1)中小正方形的边长为a-b,然后根据正方形面积公式求解,即为;
故答案为,;
(3)由(2)中的结论可得,,间的等量关系为;
(4)∵,,
∴,,
由(3)可得,
∴,
∴.
【点睛】
本题主要考查完全平方公式的应用,熟练掌握完全平方公式是解题的关键.
20.(1)运算程序为,化简后的结果为;(2)当输入的数a=﹣5时,输出结果是.
【解析】
(1)根据图中的数据,可以写出相应的运算程序,然后化简即可;
(2)将a=﹣5代入化简后的式子即可解答本题.
【详解】
解:(1)由题意可得,
计算程序为:,
,
即运算程序为,化简后的结果为;
(2)当a=﹣5时,输出结果为:
,
即当输入的数a=﹣5时,输出结果是.
【点睛】
本题考查了单项式乘多项式,合并同类项,解答本题的关键是明确整式混合运算的计算方法.
21.(1)铺设地砖的面积是22a2+16ab+2b2平方米;(2)202平方米.
【解析】
(1)根据长方形的面积减去空白的面积表示出铺设地砖的面积即可;
(2)把a与b的值代入计算即可求出值.
【详解】
解:(1)根据题意得:铺设地砖的面积为:
(6a+2b)(4a+2b)-2(a+b)2
=24a2+20ab+4b2-2a2-4ab-2b2
=22a2+16ab+2b2(平方米);
(2)当a=2,b=3时,原式=88+96+18=202(平方米).
【点睛】
本题考查了完全平方式,以及多项式乘多项式,熟练掌握运算法则及公式是解本题的关键.
22.(1)2,6;(2)5,17;(3),理由见解析
【解析】
(1)大正方形的边长为x+y,小正方的边长为x-y,由面积可求出正方形的边长;
(2)小长方形两边之和为正方形的边长,再由完全平方公式求解即可;
(3)根据大、小正方形和4个直角三角形的面积之间的关系得出结论.
【详解】
解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴,,
又∵,
∴,,
故答案为:2,6;
(2)大正方形的边长为,
∵,
∴,
故答案为:5,17;
(3),,三边的数量关系为.
理由如下:由拼图可得,小正方形的边长为,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
,
即.
【点睛】
本题考查完全平方公式的几何背景,理清各个图形面积之间的关系是解决问题的关键,用代数式表示各个部分的面积是得出结论的前提.
23.(1)①;②-1;(2)●为+或-
【解析】
(1)①利用平方差公式计算后,再合并同类项可得结果;②利用平方差公式计算后,再合并同类项可得结果为,根据结果是一个常数,可得,从而可得
(2)将代入,由题意可得,即,从而可得●为+或-
【详解】
解:(1)①
②原式
若结果是一个常数
(2)
原式
●为+或-
【点睛】
本题(1)主要考查平方差公式的应用及合并同类项;(2)主要考查整式的混合运算,熟记运算法则是解决本题的关键
24.(1), ;(2)77;(3)17
【解析】
(1)由图中正方形和长方形的面积关系,可得答案;
(2)根据,将a-b=8,ab=13代入进行计算即可;
(3)根据和 ,可求得图 中阴影部分的面积 .
【详解】
解:(1)由图可得,, .
(2),
所以的值为77.
(3)由图可得:
所以图中阴影部分的面积为17.
【点睛】
本题考查了完全平方公式的几何背景,数形结合、恰当进行代数式变形是解答本题的关键.
25.(1)998001;(2)1
【解析】
(1)根据完全平方公式即可求出答案.
(2)根据平方差公式即可求出答案.
【详解】
解:(1)9992=(1000-1)2
=10002-2×1000×1+1
=1000000-2000+1
=998001;
(2)20182-2017×2019=20182-(2018-1)(2018+1)
=20182-20182+1
=1.
【点睛】
本题考查完全平方公式以及平方差公式,解题的关键是熟练运用乘法公式,本题属于基础题型.
26.(1),;(2);(3)
【解析】
(1)方法1:两个正方形面积之和,方法2:大正方形面积-两个小长方形面积;
(2)由题意可直接得到;
(3)由,化简成,的形式,再代入数据即可求阴影部分的面积.
【详解】
(1)由题意可得:
方法1: , 方法2:,
故答案为:,;
(2),
故答案为:;
(3)
,
∵,,
.
【点睛】
本题考查了完全平方公式的几何背景,用代数式表示图形的面积是本题的关键.
27.(1)方法一:(m+n)2 4mn,方法二:(m n)2;(2)(m+n)2 4mn=(m n)2;(3)64.
【解析】
(1)观察图形可确定:方法一:大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为:(m+n)2-4mn.方法二:图2中阴影部分为正方形,其边长为m-n,进而得中间阴影部分的面积为:(m-n)2;
(2)由第(1)题可知:两种方法表示同一块阴影部分面积,进而即可得到等量关系;
(3)由(2)得,将m-n=4,mn=12,代入(2)式,即可求解.
【详解】
(1)方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积为4mn,
∴中间阴影部分的面积为: (m+n)2 4mn.
方法二:∵中间阴影部分的小正方形边长为m n,
∴中间阴影部分的面积为:(m n)2;
(2)由第(1)小题的结果,可知:(m+n)2 4mn=(m n)2;
(3)∵,,
∴由(2)得:(m+n)2 4×12=42,即:(m+n)2=64.
【点睛】
本题主要考查完全平方公式与几何图形的联系,掌握几何图形面积的表示方法,是解题的关键.
28.(1)a2-b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a-b)=a2-b2;(4).
【解析】
(1)小题1:利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便计算.
【详解】
(1)利用正方形的面积公式可知:阴影部分的面积=a2-b2;
故答案为:a2-b2;
(2)由图可知矩形的宽是a-b,长是a+b,所以面积是(a+b)(a-b);
故答案为:a-b,a+b,(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2(等式两边不能交换位置);
故答案为:(a+b)(a-b)=a2-b2;
(4)(1﹣ )(1﹣)(1﹣)…(1﹣)(1﹣)
=(1-)(1+)(1-)(1+)(1-)(1+)…(1-)(1+)(1-)(1+)
=×
=
.
【点睛】
此题考查平方差公式,解题关键在于掌握两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式.
29.(1)扩大后长方形的面积是cm2;(2)21.
【解析】
(1)先表示出长方形的宽,再表示出扩大后的长和宽,求面积即可;(2)将代入(1)中结果计算即可.
【详解】
解:(1)=
答:扩大后长方形的面积是cm2;
(2)当时,原式
【点睛】
本题考查了整式乘法的实际应用,正确理解题意,表示出长方形的长和宽是解题的关键.
30.(1) 4a2+4ab+b2.(2) 5a2+8ab+3b2.
【解析】
(1)运用正方形面积公式,即可得到剪去正方形的面积;
(2)依据拼成的长方形的长为3a+2b+(2a+b)=5a+3b,宽为3a+2b-(2a+b)=a+b,即可得到其面积.
【详解】
(1)剪去正方形的面积为(2a+b)2=4a2+4ab+b2;
(2)∵拼成的长方形的长为3a+2b+(2a+b)=5a+3b,
宽为3a+2b-(2a+b)=a+b,
∴拼成的长方形的面积为(5a+3b)(a+b)=5a2+8ab+3b2.
【点睛】
本题主要考查平方差公式的几何意义,用两种方法表示阴影部分的面积是解决此类问题的关键.
31.(1),;(2)
【解析】
根据由于欢欢抄错了第一个多项式中的a符号,得出的结果为,可知,于是;再根据乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为,可知常数项是,可知,可得到,解关于的方程组即可求出a、b的值;
把a、b的值代入原式求出整式乘法的正确结果.
【详解】
根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为,
那么,
可得
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为,
可知
即,
可得,
解关于的方程组,可得,;
正确的式子:
【点睛】
本题主要是考查多项式的乘法,正确利用法则是正确解决问题的关键.
32.(1);(2)318
【解析】
(1)根据题意可得等量关系:①500分的基本分-操作66次扣66x分+完成2列加2y分=634分,②500分的基本操作基本分-操作102次扣102x分+完成5列加5y分=898分,根据等量关系列出方程求解即可;
(2)设共操作了a次,根据总列数得分-操作分=实际得分-基本分,列方程即可求解.
【详解】
解:(1)由题意得:
整理得:
解得:
(2)设他一共操作了a次,
则10×100-a×1=1 182-500,解得a=318.
答:他一共操作了318次.
33.验证(1)(–1)2+02+12+22+32的结果是5的3倍;(2)见解析;延伸任意三个连续整数的平方和被3除的余数是2,理由见解析.
【解析】
(1)直接计算这个算式的值;(2)先用代数式表示出这几个连续整数的平方和,再化简,根据代数式的形式作出结论.
【详解】
解:验证(1)∵=1+0+1+4+9=15=5×3,
∴结果是5的3倍.
(2).
∵n为整数,
∴这个和是5的倍数.
延伸 余数是2,理由:设中间的整数为n,被3除余2.
考点:完全平方公式,整式的加减.
答案第1页,共2页
1.(2021·河北唐山·七年级期中)计算:
(1)2-2+(3721﹣4568)0
(2)(-x2)3+(-3x2)2 x2
2.(2021·河北保定·七年级期中)计算或化简:
(1);
(2);
(3).
3.(2021·河北保定·七年级期中)计算:
(1) (2)
(3) (4)
(5)先化简,再求值,其中,.
4.(2021·河北保定·七年级期中)先化简,再求值:,其中,.
5.(2021·河北唐山·七年级期中)计算:(1);
(2).
6.(2021·河北邯郸·七年级期中)运用整式乘法公式计算
(1)899901
(2)-124122
7.(2021·河北邯郸·七年级期中)(1)
(2)
8.(2021·河北秦皇岛·七年级期中)计算:
(1)(2a+5b)(2a-5b)-(a-3b)2.
(2)利用乘法公式进行简便计算:
9.(2021·河北石家庄·七年级期中)(1)
(2)
(3)解方程组
10.(2021·河北·石家庄市栾城区教育局教研室七年级期中)(1)解方程组.
(2)计算.
11.(2021·河北秦皇岛·七年级期中)计算
(1)
(2)
(3)求的值,其中x=2.
12.(2021·河北·曲阳县教育和体育局教研室七年级期中)计算:(1);
(2);
(3)先化简,再求值:,其中.
13.(2021·河北·石家庄市栾城区教育局教研室七年级期中)先化简,再求值:,其中.
14.(2021·河北邢台·七年级期中)化简:.
15.(2021·河北邯郸·七年级期中)计算:
(1)
(2)
16.(2021·河北石家庄·七年级期中)已知x2﹣3x=1,求代数式(x﹣1)(3x+1)﹣(x+2)2﹣4的值.
17.(2021·河北衡水·七年级期中)已知,求代数式的值.
18.(2021·河北唐山·七年级期中)阅读:已知正整数a、b、c,显然,当同底数时,指数大的幂也大,若对于同指数,不同底数的两个幂和,当时,则有,根据上述材料,回答下列问题.
(1)比较大小:__________(填写>、<或=).
(2)比较与的大小(写出比较的具体过程).
(3)计算.
19.(2021·河北保定·七年级期中)学完整式的乘法公式后,爱思考的小丽同学为了探究公式之间的联系,她把一个长为,宽为的长方形沿图1中虚线用剪刀平均分成四个小长方形,然后拼成一个大正方形(如图2).请你根据小丽的操作回答下列问题:
(1)图1中每个小长方形的长和宽分别为______,图2中大正方形的边长为______,中间小正方形(阴影部分)的边长为______(均用含,的式子表示);
(2)小丽发现可以用两种方法求图2中小正方形(阴影部分)的面积,请你帮她写出来(直接用含,的式子表示,不必化简):
方法1:________________________,方法2:________________________;
(3)根据(2)中的结论,探究,,间的等量关系;
(4)根据(3)中的等量关系,解决如下问题:知,满足,,请求出的值.
20.(2021·河北唐山·七年级期中)任意给定一个非零数,按下列程序计算.
(1)请用含的代数式表示计算程序,并给予化简;
(2)当输入的数a=-5时,求输出结果.
21.(2021·河北唐山·七年级期中)某学校教学楼前有一块长为米,宽为米的长方形空地要铺地砖,如图所示,空白的甲、乙两正方形区域是草坪,不需要铺地砖.两正方形区域的边长均为米.
(1)求铺设地砖的面积是多少平方米;
(2)当,时,需要铺地砖的面积是多少?
22.(2021·河北·石家庄市栾城区教育局教研室七年级期中)如图1,用4个相同边长是、的长方形和中间一个小正方形组成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则值为__________;则的值为__________;
(2)若小长方形两边长为和,则大正方形的边长为___________;
若满足,则的值为__________;
(3)如图2,正方形的边长是,它由四个直角边长分别是,的直角三角形和中间一个小正方形组成的,猜想,,三边的数量关系,并说明理由.
23.(2021·河北邢台·七年级期中)在化简题目中,表示,,,四个运算符号中的某一个,◆表示二次项的系数.
(1)若●表示“”;
①把◆猜成时,请化简;
②若结果是一个常数,请说明◆表示的数是几?
(2)若◆表示数,当时,的值为,请推算●所表示的符号.
24.(2021·河北保定·七年级期中)两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为;若再在图①中大正方形的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为.
(1)用含a、b的代数式分别表示、;
(2)若,,求的值;
(3)用a、b的代数式表示;并当时,求出图③中阴影部分的面积.
25.(2021·河北唐山·七年级期中)请你参考黑板中老师的讲解,用乘法公式进行简便计算:
(1)
(2)20182-20172019
26.(2021·河北邢台·七年级期中)(1)根据图1中条件,试用两种不同方法表示两个阴影图形的面积的和.
方法1:_________.方法2:_________.
(2)从中你能发现什么结论?请用等式表示出来:_________.
(3)利用(2)中结论解决下面的问题:如图2,两个正方形边长分别为a、b,如果a+b=10,ab=24,求阴影部分的面积.
27.(2021·河北秦皇岛·七年级期中)如图,①是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全一样的小长方形,再按照图②围成一个较大的正方形.
(1)请用两种方法表示图②中阴影部分的面积(只需要表示,不必化简);
(2)比较(1)中的两种结果,你能得到怎样的等量关系式?
(3)请你用(2)中得到的等量关系解决下列问题:如果.,求的值.
28.(2021·河北保定·七年级期中)乘法公式的探究及应用.
(1)如图 1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式)
(3)比较图 1,图 2 的阴影部分面积,可以得到乘法公式 (用式子表达)
(4)应用所得的公式计算:(1﹣ )(1﹣)(1﹣)…(1﹣)(1﹣)
29.(2021·河北唐山·七年级期中)一个长方形的长为2xcm,宽比长少4cm,若将长方形的长和宽都扩大3cm.
(1)求扩大后长方形的面积是多少?(用含x的代数式表示)
(2)若,求扩大后长方形的面积是多少?
30.(2021·河北邯郸·七年级期中)如图,在图(1)中的正方形中剪去一个边长为2a+b的正方形,将剩余的部分按图(2)的方式拼成一个长方形
(1)求剪去正方形的面积;
(2)求拼成的长方形的长、宽以及它的面积.
31.(2021·河北唐山·七年级期中)欢欢与乐乐两人共同计算,欢欢抄错为,得到的结果为;乐乐抄错为,得到的结果为.
式子中的a、b的值各是多少?
请计算出原题的正确答案.
32.(2021·河北·曲阳县教育和体育局教研室七年级期中)电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段 第二时段
完成列数 2 5
分数 634 898
操作次数 66 102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
33.(2021·河北衡水·七年级期中)发现 任意五个连续整数的平方和是5的倍数.
验证 (1)(–1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
试卷第1页,共3页
参考答案:
1.(1);(2)8x6
【解析】
(1)先算负整数指数幂和零指数幂,再算加法,即可求解;
(2)先算幂的乘方和积的乘方,进而即可求解.
【详解】
解:(1)原式=+1
=;
(2)原式=-x6+9x4 x2
=-x6+9x6
=8x6.
【点睛】
本题主要考查实数的混合运算以及整式的运算,掌握负整数指数幂和零指数幂的性质以及幂的乘方和积的乘方法则,是解题的关键.
2.(1)-4;(2);(3)
【解析】
(1)根据负指数幂及零次幂可直接进行求解;
(2)根据积的乘方、单项式除以单项式及整式的乘法可直接进行求解;
(3)根据多项式乘多项式可进行求解.
【详解】
解:(1)原式=;
(2)原式=;
(3)原式=.
【点睛】
本题主要考查负指数幂、零次幂、分式的运算、多项式乘多项式及单项式除单项式,熟练掌握负指数幂、零次幂、分式的运算、多项式乘多项式及单项式除单项式是解题的关键.
3.(1);(2);(3);(4);(5),
【解析】
(1)根据平方差公式即可求解;
(2)根据单项式的除法法则即可求解;
(3)先算零指数幂和负整数指数幂,再算乘法,即可求解;
(4)先算单项式的乘除法,再合并同类项即可求解;
(5)先化简括号内的整式,再算整式的除法,最后代入求值,即可.
【详解】
解:(1)原式=
=;
(2)原式=
=;
(3)原式=
=;
(4)原式=
=
=;
(5)原式=
=
=
=,
当,时,原式=.
【点睛】
本题主要考查实数的混合运算,整式的化简求值,零指数幂和负整数指数幂的性质,熟练掌握整式的混合运算法则和乘法公式,是解题的关键.
4.,0
【解析】
先对整式进行化简,然后再把x、y的值代入求解即可.
【详解】
解:原式=
=
=,
把,代入得:
原式=.
【点睛】
本题主要考查整式的化简求值,熟练掌握整式的运算是解题的关键.
5.(1);(2).
【解析】
(1)根据积的乘方、单项式乘单项式和同底数幂的除法可以解答本题;
(2)根据完全平方公式、平方差公式可以解答本题.
【详解】
解:(1)
;
(2)
.
【点睛】
本题考查了整式的混合运算,涉及到积的乘方、同底数幂的除法、乘法公式等,解答本题的关键是明确它们各自的计算方法.
6.(1)809999;(2)1
【解析】
(1)利用平方差公式求解即可;
(2)先利用平方差公式计算,进而即可求解.
【详解】
(1)899901
=(900-1)(900+1)
=-1
=810000-1
=809999;
(2)-124122
=-(123+1)(123-1)
=-
=1.
【点睛】
本题考查了运用整式乘法公式计算,掌握整式的乘法公式是解题的关键.
7.(1);(2)
【解析】
(1)根据整式的乘法对式子进行运算即可;
(2)根据整式的除法对式子进行运算即可.
【详解】
(1)解:
(2)解:
【点睛】
此题主要考查了整式的乘除运算,熟练掌握整式乘除的运算法则是解题的关键.
8.(1)3a2+6ab-34b2;(2)-1
【解析】
(1)根据平方差公式和完全平方公式展开化简可以解答本题;
(2)根据平方差公式可以解答本题;
【详解】
(1)(2a+5b)(2a-5b)-(a-3b)2
=4a2-25b2-a2+6ab-9b2
=3a2+6ab-34b2
(2)
=
=
=-1.
【点睛】
本题考查整式的混合运算,解题的关键是明确平方差和完全平方公式的计算方法.
9.(1)2;(2)-a3b6 ;(3)
【解析】
(1)先计算乘方,负指数幂,零指数幂,然后再计算加减即可;
(2)根据积的乘方法则计算,在算单项式与单项式相乘法则计算,最后合并同类项即可;
(3)先标号,由①得x=8-3y③,利用代入消元法解方程组即可.
【详解】
(1)解:,
=-1+4-1,
=2;
(2)解:,
=8a3b6-9ab2×a2b4,
=8a3b6-9a3b6,
=-a3b6;
(3)解:,
由 ①得x=8-3y③,
把③代入②得:,
解得:,
把代入③得:.
∴原方程组的解是.
【点睛】
本题考查实数运算,乘方,负指数幂,零指数幂,整式的幂指数混合运算,解得乘方,单项式乘单项式,合并同类项,二元一次方程组解法,掌握实数运算,乘方,负指数幂,零指数幂,整式的幂指数混合运算,解得乘方,单项式乘单项式,合并同类项,二元一次方程组解法是解题关键.
10.(1);(2)
【解析】
(1)利用求解二元一次方程组的代入消元法求解即可;
(2)利用积的乘方等于乘方的积以及幂的乘方进行化简,然后合并求值即可.
【详解】
解:(1),
把代入②,
得:,
解得:,
把代入①得:,
故原方程组的解为:.
(2)解:原式
.
【点睛】
本题主要考查解二元一次方程组、积的乘方以及幂的乘方的运算,熟练掌握方法以及积的乘方的运用是解题关键.
11.(1) (2) (3) ,-14;
【解析】
(1)先将原式运用平方差公式进行展开,继而利用提公因式法进行计算即可;
(2)利用单项乘以多项式的运算法则进行计算即可;
(3)先将原式进行化简,再将x的值代入进行求解即可;
【详解】
(1)原式=
(2)原式=
(3)原式=
,
将 代入得:
【点睛】
本题考查了因式分解、单项式乘以多项式、整式的混合运算、多项式乘以多项式,正确掌握运算法则是解题的关键;
12.(1);(2);(3),-8
【解析】
(1)按照单项式的乘法法则计算即可;
(2)运用完全平方公式,平方差公式展开化简即可;
(3)运用乘法公式化简,后代入求值
【详解】
(1)
=
=;
(2)
=
=
(3)解:原式
.
当时,原式.
【点睛】
本题考查了整式的乘法,完全平方公式,平方差公式,化简求值,熟练运用整式的乘法法则,完全平方公式,平方差公式进行化简是解题的关键.
13.
【解析】
先根据完全平方公式和平方差公式进行化简,再将代入即可
【详解】
解:
当时,原式=6+10=16.
【点睛】
本题考查了整式的化简求值,熟练掌握运算法则和计算公式是解题的关键
14.
【解析】
直接利用同底数幂的乘法,除法,积的乘方,幂的乘方计算化简即可.
【详解】
解:原式=
=
【点睛】
本题主要考查整式的混合运算,熟练掌握同底数幂的乘除法,幂的乘方,积的乘方的运算法则是解题的关键.
15.(1)-4y-2;(2)-4mn
【解析】
(1)根据多项式的乘法法则展开后再合并同类项即可得到解答;
(2)根据平方差公式和完全平方公式展开后再合并同类项即可得到解答.
【详解】
(1)解:原式=(y3+2y2+y-2y2-4y-2)-(y3+y)
=y3+2y2+y- 2y2-4y-2-y3-y
=-4y-2
(2)原式=(m2-4n2)-(m2+4mn+4n2)+8n2
=m2-4n2-m2-4mn- 4n2+8n2
=-4mn
【点睛】
本题考查多项式的乘法,灵活运用多项式乘法法则和乘法公式计算是解题关键.
16.﹣7.
【解析】
原式利用整式的乘法公式和完全平方公式展开后化简,再把x2﹣3x=1整体代入求得数值即可.
【详解】
解:原式=3x2﹣2x﹣1﹣(x2+4x+4)﹣4
=3x2﹣2x﹣1﹣x2﹣4x﹣4﹣4
=2x2﹣6x﹣9.
∵x2﹣3x=1.
∴原式=2(x2﹣3x)﹣9=2﹣9=﹣7.
【点睛】
本题考查了整式的化简求值,属于基本题型,熟练掌握整式的混合运算法则是解题的关键.
17.12
【解析】
将代数式应用完全平方公式和平方差公式展开后合并同类项,将整体代入求值.
【详解】
解:∵,∴.
∴
.
18.(1)>;(2)<;(3)-4
【解析】
(1)根据同指数的幂底数越大幂越大,可得答案;
(2)根据幂的乘方,可得指数相同的幂,根据底数越大幂越大,可得答案;
(3)先根据积的乘方逆运算进行运算,再进行减法运算即可得出答案.
【详解】
解:(1)∵5>4,
∴>,
故答案为:>;
(2)∵233=(23)11=811,322=(32)11=911,
又∵8<9,
∴<.
(3)
【点睛】
本题考查了幂的乘方以及积的乘方,利用同指数的幂底数越大幂越大是解题关键.
19.(1)a、b,a+b,a-b;(2),;(3);(4)6
【解析】
(1)由“一个长为,宽为的长方形沿图1中虚线用剪刀平均分成四个小长方形”可得每个长方形的长和宽,然后根据图形可求解问题;
(2)根据图形及割补法可进行求解问题;
(3)由(2)可直接进行求解;
(4)由,可得,,然后根据(3)的关系式可进行求解.
【详解】
解:(1)由题意得:
图1中每个小长方形的长和宽分别为a、b,图2中大正方形的边长为a+b,中间小正方形(阴影部分)的边长为a-b;
故答案为a、b,a+b,a-b;
(2)方法1:利用大正方形的面积减去四个小长方形的面积=小正方形的面积,即为;
方法2:由(1)中小正方形的边长为a-b,然后根据正方形面积公式求解,即为;
故答案为,;
(3)由(2)中的结论可得,,间的等量关系为;
(4)∵,,
∴,,
由(3)可得,
∴,
∴.
【点睛】
本题主要考查完全平方公式的应用,熟练掌握完全平方公式是解题的关键.
20.(1)运算程序为,化简后的结果为;(2)当输入的数a=﹣5时,输出结果是.
【解析】
(1)根据图中的数据,可以写出相应的运算程序,然后化简即可;
(2)将a=﹣5代入化简后的式子即可解答本题.
【详解】
解:(1)由题意可得,
计算程序为:,
,
即运算程序为,化简后的结果为;
(2)当a=﹣5时,输出结果为:
,
即当输入的数a=﹣5时,输出结果是.
【点睛】
本题考查了单项式乘多项式,合并同类项,解答本题的关键是明确整式混合运算的计算方法.
21.(1)铺设地砖的面积是22a2+16ab+2b2平方米;(2)202平方米.
【解析】
(1)根据长方形的面积减去空白的面积表示出铺设地砖的面积即可;
(2)把a与b的值代入计算即可求出值.
【详解】
解:(1)根据题意得:铺设地砖的面积为:
(6a+2b)(4a+2b)-2(a+b)2
=24a2+20ab+4b2-2a2-4ab-2b2
=22a2+16ab+2b2(平方米);
(2)当a=2,b=3时,原式=88+96+18=202(平方米).
【点睛】
本题考查了完全平方式,以及多项式乘多项式,熟练掌握运算法则及公式是解本题的关键.
22.(1)2,6;(2)5,17;(3),理由见解析
【解析】
(1)大正方形的边长为x+y,小正方的边长为x-y,由面积可求出正方形的边长;
(2)小长方形两边之和为正方形的边长,再由完全平方公式求解即可;
(3)根据大、小正方形和4个直角三角形的面积之间的关系得出结论.
【详解】
解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴,,
又∵,
∴,,
故答案为:2,6;
(2)大正方形的边长为,
∵,
∴,
故答案为:5,17;
(3),,三边的数量关系为.
理由如下:由拼图可得,小正方形的边长为,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
,
即.
【点睛】
本题考查完全平方公式的几何背景,理清各个图形面积之间的关系是解决问题的关键,用代数式表示各个部分的面积是得出结论的前提.
23.(1)①;②-1;(2)●为+或-
【解析】
(1)①利用平方差公式计算后,再合并同类项可得结果;②利用平方差公式计算后,再合并同类项可得结果为,根据结果是一个常数,可得,从而可得
(2)将代入,由题意可得,即,从而可得●为+或-
【详解】
解:(1)①
②原式
若结果是一个常数
(2)
原式
●为+或-
【点睛】
本题(1)主要考查平方差公式的应用及合并同类项;(2)主要考查整式的混合运算,熟记运算法则是解决本题的关键
24.(1), ;(2)77;(3)17
【解析】
(1)由图中正方形和长方形的面积关系,可得答案;
(2)根据,将a-b=8,ab=13代入进行计算即可;
(3)根据和 ,可求得图 中阴影部分的面积 .
【详解】
解:(1)由图可得,, .
(2),
所以的值为77.
(3)由图可得:
所以图中阴影部分的面积为17.
【点睛】
本题考查了完全平方公式的几何背景,数形结合、恰当进行代数式变形是解答本题的关键.
25.(1)998001;(2)1
【解析】
(1)根据完全平方公式即可求出答案.
(2)根据平方差公式即可求出答案.
【详解】
解:(1)9992=(1000-1)2
=10002-2×1000×1+1
=1000000-2000+1
=998001;
(2)20182-2017×2019=20182-(2018-1)(2018+1)
=20182-20182+1
=1.
【点睛】
本题考查完全平方公式以及平方差公式,解题的关键是熟练运用乘法公式,本题属于基础题型.
26.(1),;(2);(3)
【解析】
(1)方法1:两个正方形面积之和,方法2:大正方形面积-两个小长方形面积;
(2)由题意可直接得到;
(3)由,化简成,的形式,再代入数据即可求阴影部分的面积.
【详解】
(1)由题意可得:
方法1: , 方法2:,
故答案为:,;
(2),
故答案为:;
(3)
,
∵,,
.
【点睛】
本题考查了完全平方公式的几何背景,用代数式表示图形的面积是本题的关键.
27.(1)方法一:(m+n)2 4mn,方法二:(m n)2;(2)(m+n)2 4mn=(m n)2;(3)64.
【解析】
(1)观察图形可确定:方法一:大正方形的面积为(m+n)2,四个小长方形的面积为4mn,中间阴影部分的面积为:(m+n)2-4mn.方法二:图2中阴影部分为正方形,其边长为m-n,进而得中间阴影部分的面积为:(m-n)2;
(2)由第(1)题可知:两种方法表示同一块阴影部分面积,进而即可得到等量关系;
(3)由(2)得,将m-n=4,mn=12,代入(2)式,即可求解.
【详解】
(1)方法一:∵大正方形的面积为(m+n)2,四个小长方形的面积为4mn,
∴中间阴影部分的面积为: (m+n)2 4mn.
方法二:∵中间阴影部分的小正方形边长为m n,
∴中间阴影部分的面积为:(m n)2;
(2)由第(1)小题的结果,可知:(m+n)2 4mn=(m n)2;
(3)∵,,
∴由(2)得:(m+n)2 4×12=42,即:(m+n)2=64.
【点睛】
本题主要考查完全平方公式与几何图形的联系,掌握几何图形面积的表示方法,是解题的关键.
28.(1)a2-b2;(2)a-b,a+b,(a+b)(a-b);(3)(a+b)(a-b)=a2-b2;(4).
【解析】
(1)小题1:利用正方形的面积公式就可求出;
(2)仔细观察图形就会知道长,宽,由面积公式就可求出面积;
(3)建立等式就可得出;
(4)利用平方差公式就可方便计算.
【详解】
(1)利用正方形的面积公式可知:阴影部分的面积=a2-b2;
故答案为:a2-b2;
(2)由图可知矩形的宽是a-b,长是a+b,所以面积是(a+b)(a-b);
故答案为:a-b,a+b,(a+b)(a-b);
(3)(a+b)(a-b)=a2-b2(等式两边不能交换位置);
故答案为:(a+b)(a-b)=a2-b2;
(4)(1﹣ )(1﹣)(1﹣)…(1﹣)(1﹣)
=(1-)(1+)(1-)(1+)(1-)(1+)…(1-)(1+)(1-)(1+)
=×
=
.
【点睛】
此题考查平方差公式,解题关键在于掌握两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做平方差公式.
29.(1)扩大后长方形的面积是cm2;(2)21.
【解析】
(1)先表示出长方形的宽,再表示出扩大后的长和宽,求面积即可;(2)将代入(1)中结果计算即可.
【详解】
解:(1)=
答:扩大后长方形的面积是cm2;
(2)当时,原式
【点睛】
本题考查了整式乘法的实际应用,正确理解题意,表示出长方形的长和宽是解题的关键.
30.(1) 4a2+4ab+b2.(2) 5a2+8ab+3b2.
【解析】
(1)运用正方形面积公式,即可得到剪去正方形的面积;
(2)依据拼成的长方形的长为3a+2b+(2a+b)=5a+3b,宽为3a+2b-(2a+b)=a+b,即可得到其面积.
【详解】
(1)剪去正方形的面积为(2a+b)2=4a2+4ab+b2;
(2)∵拼成的长方形的长为3a+2b+(2a+b)=5a+3b,
宽为3a+2b-(2a+b)=a+b,
∴拼成的长方形的面积为(5a+3b)(a+b)=5a2+8ab+3b2.
【点睛】
本题主要考查平方差公式的几何意义,用两种方法表示阴影部分的面积是解决此类问题的关键.
31.(1),;(2)
【解析】
根据由于欢欢抄错了第一个多项式中的a符号,得出的结果为,可知,于是;再根据乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为,可知常数项是,可知,可得到,解关于的方程组即可求出a、b的值;
把a、b的值代入原式求出整式乘法的正确结果.
【详解】
根据题意可知,由于欢欢抄错了第一个多项式中的a的符号,得到的结果为,
那么,
可得
乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为,
可知
即,
可得,
解关于的方程组,可得,;
正确的式子:
【点睛】
本题主要是考查多项式的乘法,正确利用法则是正确解决问题的关键.
32.(1);(2)318
【解析】
(1)根据题意可得等量关系:①500分的基本分-操作66次扣66x分+完成2列加2y分=634分,②500分的基本操作基本分-操作102次扣102x分+完成5列加5y分=898分,根据等量关系列出方程求解即可;
(2)设共操作了a次,根据总列数得分-操作分=实际得分-基本分,列方程即可求解.
【详解】
解:(1)由题意得:
整理得:
解得:
(2)设他一共操作了a次,
则10×100-a×1=1 182-500,解得a=318.
答:他一共操作了318次.
33.验证(1)(–1)2+02+12+22+32的结果是5的3倍;(2)见解析;延伸任意三个连续整数的平方和被3除的余数是2,理由见解析.
【解析】
(1)直接计算这个算式的值;(2)先用代数式表示出这几个连续整数的平方和,再化简,根据代数式的形式作出结论.
【详解】
解:验证(1)∵=1+0+1+4+9=15=5×3,
∴结果是5的3倍.
(2).
∵n为整数,
∴这个和是5的倍数.
延伸 余数是2,理由:设中间的整数为n,被3除余2.
考点:完全平方公式,整式的加减.
答案第1页,共2页
同课章节目录
