2021-2022学年苏科版九年级下册数学第6章图形的相似单元测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级下册数学第6章图形的相似单元测试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 236.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 23:34:40 | ||
图片预览



文档简介
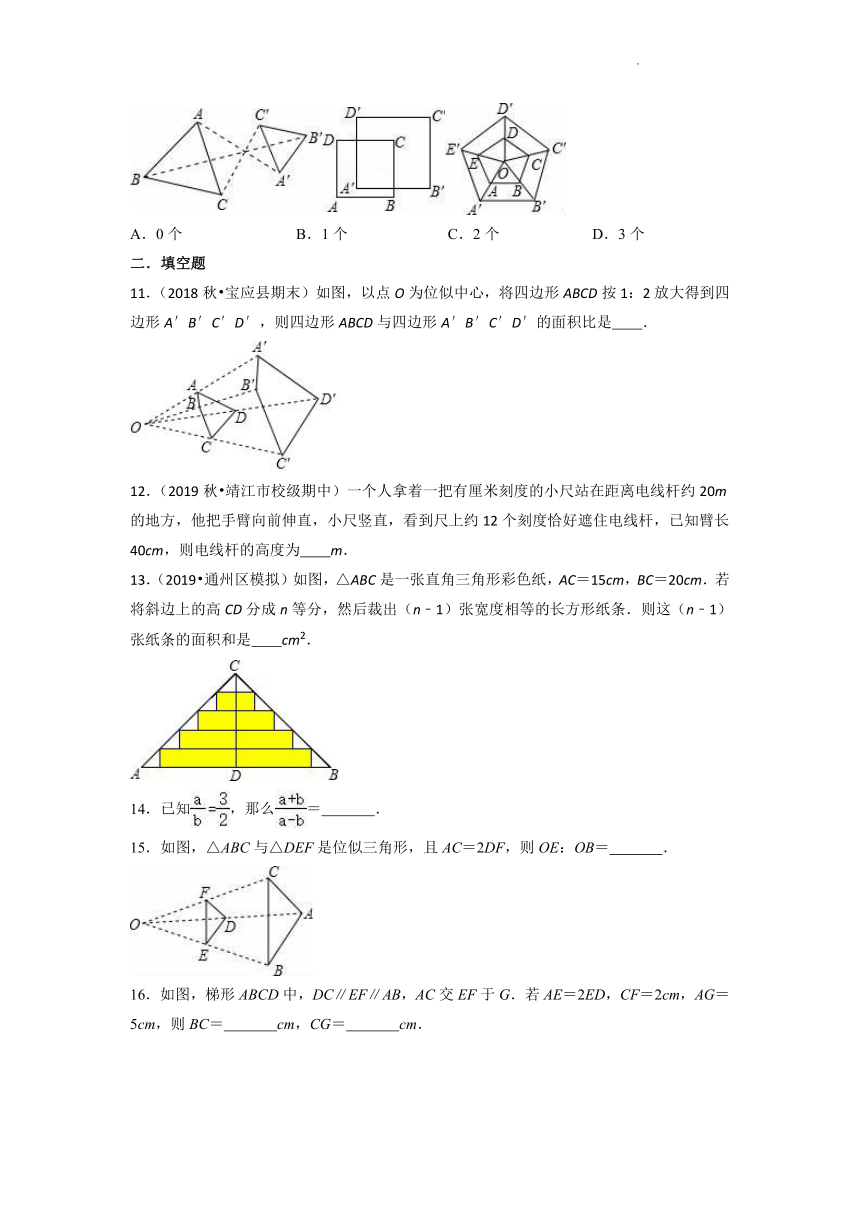
《第6章 图形的相似》单元测试题
一.选择题
1.已知mn=ef,则下列式子错误的是( )
A. B. C. D.
2.下列四条线段成比例得是( )
A.4、6、5、10 B.12、8、16、20 C.1、 D.、2
3.已知:如图,DE∥AC,DF∥AB,则下列比例式中正确的是( )
A. B. C. D.
4.下列四个三角形,与已知图构成相似的三角形是( )
A. B.
C. D.
5.如图,要使,需补充的条件不能是( )
A. B.
C. D.
6.如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边上的点F处,若AD=2,BC=6,则EF的值是( )
A.2 B. C. D.2
7.如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
8.在△ABC中,DE∥BC,且分△ABC为面积相等的两部分,则DE:BC的值为( )
A.1: B.1:2 C.1:3 D.:1
9.已知甲、乙两地图的比例尺分别为1:5000和1:20 000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2 B.2:5 C.1:4 D.4:1
10.下列3个图形中是位似图形的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
11.(2018秋 宝应县期末)如图,以点O为位似中心,将四边形ABCD按1:2放大得到四边形A′B′C′D′,则四边形ABCD与四边形A′B′C′D′的面积比是 .
12.(2019秋 靖江市校级期中)一个人拿着一把有厘米刻度的小尺站在距离电线杆约20m的地方,他把手臂向前伸直,小尺竖直,看到尺上约12个刻度恰好遮住电线杆,已知臂长40cm,则电线杆的高度为 m.
13.(2019 通州区模拟)如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD分成n等分,然后裁出(n﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是 cm2.
14.已知,那么= .
15.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE:OB= .
16.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC= cm,CG= cm.
17.如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是 .(用含k的式子表示)
18.如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= cm.
三.解答题
19.线段AB的长度为10cm,点P为其一个黄金分割点,求AP的长.
20.(2020秋 宝应县月考)如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
21.(2020 镇江模拟)如图所示,Rt△ABC中∠C=90°,∠A=60°,D、E分别为AC、BC的中点,以DE为直角边画出等腰直角三角形△DEF.
(1)证△CDE与△BEH相似;
(2)若DE=1,求AB的长.
22.(2019秋 东台市期末)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
23.在边长为1的正方形网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?由此,你还能找出图中相似的三角形吗?若能,请找出来,并说明理由.
24.如图:在△ABC中,AB=5,AC=4,P是AB上一点,且AP=3,若Q在AC上,试确定Q点的位置,使以A、P、Q为顶点的三角形与△ABC相似.
25.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
B 2.D 3.B 4.D 5.D 6.A 7.D8.A 9.C 10D
11.1:4.
12.6米.
13..
14.4:9.
15.解:∵△ABC与△DEF是位似三角形,
∴DF∥AC,EF∥BC
∴△OAC∽△ODF,OE:OB=OF:OC
∴OF:OC=DF:AC
∵AC=2DF
∴OE:OB=DF:AC=1:2.
故答案为:1:2.
16.6,2.5.
17.k2005(2+k).
18..
19.解:由于P为线段AB=10cm的黄金分割点,
则AP=10×=5﹣5或AP=10×=15﹣5.
故AP的长为:(5﹣5)cm或(15﹣5)cm.
20.解:(1)相似,等边三角形各角相等,各边成比例,故两这个三角形相似得到.
(2)相似,易知两三角形均为等腰直角三角形,
符合两组对应边的比相等且相应的夹角相等的两个三角形相似的判定.
21.解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴=,即=,
∴=,
解得:OC=5或x=﹣5 (舍去),
则EC=2OC=10,即⊙O直径的长是10.
22.解:∵x:y:z=3:5:7,
∴设x=3k、y=5k、z=7k,
则==.
23.解:AB==,BC=10,AC==,
AE=2,AD=,DE==,CE==,
BD==,
∴===,
===,
∴△ABC∽△ADE,△ABD∽△ACE.
24.解:∵∠A是公共角,
∴当AP:AB=AQ:AC时,△APQ∽△ABC,
即3:5=AQ:4,
解得:AQ=;
当AP:AC=AQ:AB时,△APQ∽△ACB,
即3:4=AQ:5,
解得:AQ=;
∴当AQ=或时,以A、P、Q为顶点的三角形与△ABC相似.
25.解:∵AD=2BD,S△ABC=6,
∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,
∴CG=DG,
∴BD=2EG,
∵AD=2BD,
∴AD=4EG.
设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG: S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2﹣=,
设S△FEG=x,则S四边形BEFD=﹣x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE﹣S四边形BEFD=3﹣(﹣x)=+x.
∵EG∥AD,
∴△FEG∽△FAD,
∴S△FEG:S△FAD=()2=,
∴S△FAD=16S△FEG=16x,
∴16x=+x,
解得x=,
∴S四边形BEFD=﹣x=﹣=.
一.选择题
1.已知mn=ef,则下列式子错误的是( )
A. B. C. D.
2.下列四条线段成比例得是( )
A.4、6、5、10 B.12、8、16、20 C.1、 D.、2
3.已知:如图,DE∥AC,DF∥AB,则下列比例式中正确的是( )
A. B. C. D.
4.下列四个三角形,与已知图构成相似的三角形是( )
A. B.
C. D.
5.如图,要使,需补充的条件不能是( )
A. B.
C. D.
6.如图,四边形ABCD中,AD∥BC,∠B=90°,E为AB上一点,分别以ED,EC为折痕将两个角(∠A,∠B)向内折起,点A,B恰好落在CD边上的点F处,若AD=2,BC=6,则EF的值是( )
A.2 B. C. D.2
7.如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是( )
A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
8.在△ABC中,DE∥BC,且分△ABC为面积相等的两部分,则DE:BC的值为( )
A.1: B.1:2 C.1:3 D.:1
9.已知甲、乙两地图的比例尺分别为1:5000和1:20 000,如果甲图上A、B两地的距离与乙图上C、D两地的距离恰好一样长,那么A、B两地的实际距离与C、D两地的实际距离之比为( )
A.5:2 B.2:5 C.1:4 D.4:1
10.下列3个图形中是位似图形的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题
11.(2018秋 宝应县期末)如图,以点O为位似中心,将四边形ABCD按1:2放大得到四边形A′B′C′D′,则四边形ABCD与四边形A′B′C′D′的面积比是 .
12.(2019秋 靖江市校级期中)一个人拿着一把有厘米刻度的小尺站在距离电线杆约20m的地方,他把手臂向前伸直,小尺竖直,看到尺上约12个刻度恰好遮住电线杆,已知臂长40cm,则电线杆的高度为 m.
13.(2019 通州区模拟)如图,△ABC是一张直角三角形彩色纸,AC=15cm,BC=20cm.若将斜边上的高CD分成n等分,然后裁出(n﹣1)张宽度相等的长方形纸条.则这(n﹣1)张纸条的面积和是 cm2.
14.已知,那么= .
15.如图,△ABC与△DEF是位似三角形,且AC=2DF,则OE:OB= .
16.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC= cm,CG= cm.
17.如图,顶角为36°的等腰三角形,其底边与腰的比是k,这样的三角形叫黄金三角形,已知腰长AB=1,△ABC为第一个黄金三角形,△BCD是第二个黄金三角形,△CDE是第三个黄金三角形,以此类推,第2006个黄金三角形的周长是 .(用含k的式子表示)
18.如图,在平行四边形ABCD中,AB=12cm,AD=5cm,E为AD的中点,在AB上取一点F,使△CBF∽△CDE,则AF= cm.
三.解答题
19.线段AB的长度为10cm,点P为其一个黄金分割点,求AP的长.
20.(2020秋 宝应县月考)如图,在△ABC中,CD⊥AB于D,BE⊥AC于E,试说明:
(1)△ABE∽△ACD;
(2)AD BC=DE AC.
21.(2020 镇江模拟)如图所示,Rt△ABC中∠C=90°,∠A=60°,D、E分别为AC、BC的中点,以DE为直角边画出等腰直角三角形△DEF.
(1)证△CDE与△BEH相似;
(2)若DE=1,求AB的长.
22.(2019秋 东台市期末)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB AD;
(2)求证:△AFD∽△CFE.
23.在边长为1的正方形网格中有A、B、C、D、E五个点,问△ABC与△ADE是否相似?为什么?由此,你还能找出图中相似的三角形吗?若能,请找出来,并说明理由.
24.如图:在△ABC中,AB=5,AC=4,P是AB上一点,且AP=3,若Q在AC上,试确定Q点的位置,使以A、P、Q为顶点的三角形与△ABC相似.
25.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
B 2.D 3.B 4.D 5.D 6.A 7.D8.A 9.C 10D
11.1:4.
12.6米.
13..
14.4:9.
15.解:∵△ABC与△DEF是位似三角形,
∴DF∥AC,EF∥BC
∴△OAC∽△ODF,OE:OB=OF:OC
∴OF:OC=DF:AC
∵AC=2DF
∴OE:OB=DF:AC=1:2.
故答案为:1:2.
16.6,2.5.
17.k2005(2+k).
18..
19.解:由于P为线段AB=10cm的黄金分割点,
则AP=10×=5﹣5或AP=10×=15﹣5.
故AP的长为:(5﹣5)cm或(15﹣5)cm.
20.解:(1)相似,等边三角形各角相等,各边成比例,故两这个三角形相似得到.
(2)相似,易知两三角形均为等腰直角三角形,
符合两组对应边的比相等且相应的夹角相等的两个三角形相似的判定.
21.解:延长PO到E,延长线与圆O交于点E,连接EB,AC.
∵PA=9,AB=7,
∴PB=16.
∵四边形ACEB为圆O的内接四边形,
∴∠ACP=∠E,又∠P=∠P,
∴△ACP∽△EBP,
∴=,即=,
∴=,
解得:OC=5或x=﹣5 (舍去),
则EC=2OC=10,即⊙O直径的长是10.
22.解:∵x:y:z=3:5:7,
∴设x=3k、y=5k、z=7k,
则==.
23.解:AB==,BC=10,AC==,
AE=2,AD=,DE==,CE==,
BD==,
∴===,
===,
∴△ABC∽△ADE,△ABD∽△ACE.
24.解:∵∠A是公共角,
∴当AP:AB=AQ:AC时,△APQ∽△ABC,
即3:5=AQ:4,
解得:AQ=;
当AP:AC=AQ:AB时,△APQ∽△ACB,
即3:4=AQ:5,
解得:AQ=;
∴当AQ=或时,以A、P、Q为顶点的三角形与△ABC相似.
25.解:∵AD=2BD,S△ABC=6,
∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,
∴CG=DG,
∴BD=2EG,
∵AD=2BD,
∴AD=4EG.
设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG: S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2﹣=,
设S△FEG=x,则S四边形BEFD=﹣x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE﹣S四边形BEFD=3﹣(﹣x)=+x.
∵EG∥AD,
∴△FEG∽△FAD,
∴S△FEG:S△FAD=()2=,
∴S△FAD=16S△FEG=16x,
∴16x=+x,
解得x=,
∴S四边形BEFD=﹣x=﹣=.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
