六年级数学下册课件-6.4 数学思考 人教版(共15张ppt)
文档属性
| 名称 | 六年级数学下册课件-6.4 数学思考 人教版(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 985.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
数学思考
师生握手:每2人握一次手,共握几次手?
怎么办呢?
握手实验或画点数数吧!
游戏挑战
学习目标
1.我能掌握“化繁为简、化难为易”的数学方法。
2.我能运用一定规律解决较复杂的数学问题。
3.提高归纳推理探索规律的能力。
并将两点连成一条线段
请同学们在纸上任意点上6个点
数一数你连成的线段有多少条
点数
增加 条数
总条 数
5个点连成线段的条数:1+2+3+4=10 (条)
6个点连成线段的条数:
8个点连成线段的条数:
12个点呢?20个点呢?请写出算式。
2
3
4
5
2
3
4
1
6
10
3
…
…
…
1+2+3+4+5=15 (条)
1+2+3+4+5+6+7=28(条)
1+2+3+4+5+6+7+8+9+10+11
1+2+3+4+5+6+…+18+19
2个点连成线段的条数:1(条)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
我的发现
n个点:
1+2+3+…+(n-1)
用点连线的规律:
从1开始的前(n-1)个连续自然数的和
(即从1开始加起,一直加到比点数少1的连续几个自然数的和)
我找到规律啦!
n个点最多能连成多少条线段?
101个点最多能连成多少条线段?
1+2+3+4+5+6+7+…+100
= 5050(条)
1+2+3+4+5+6+7+…+(n-1)
= n(n-1) ÷ 2(条)
=(1+100)×100÷2
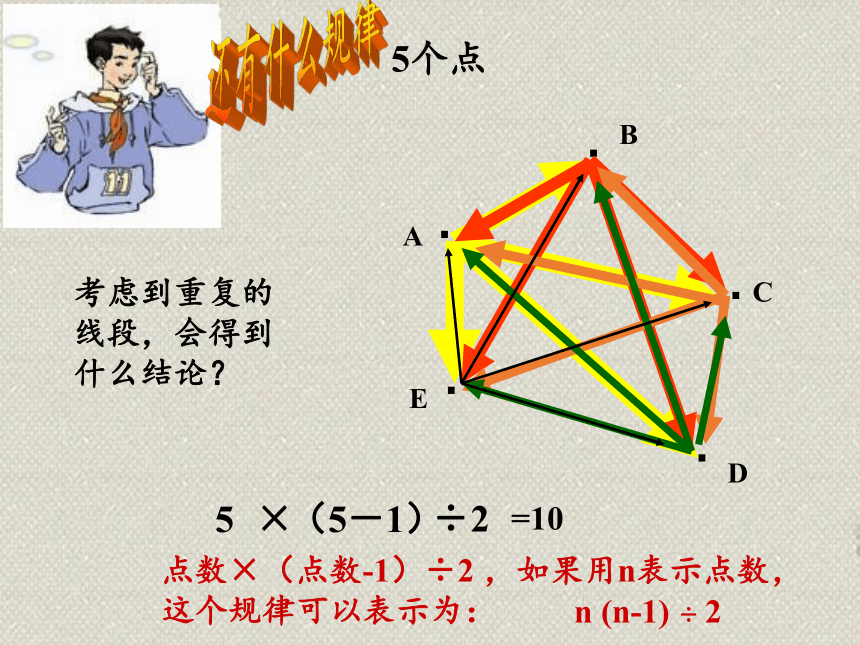
还有什么规律
考虑到重复的线段,会得到什么结论?
A
E
D
C
B
5
×
(5-1)
÷2
=10
5个点
点数×(点数-1)÷2 ,如果用n表示点数,这个规律可以表示为:
n (n-1) ÷ 2
师生(55人)握手:每2人握一次手,大家一共要握多少次手?
1+2+3+4+5+…+55=1540(次)
想一想:还有其它方法吗?
1.把下面的数列补充完整。
1,2,3,5,8,13,( )
3,6,10,15,21,( )
21
达标检测
2.摆一摆,找规律。
(1)第6个图形是什么图形?
(2)第7个图形需要用多少根小棒?第n个图形呢
(15根)
…
(2n+1根)
火眼金睛:我会辨
1.为迎接下五屯中心小学校园文化艺术节,节目筹备组15人到会议室开会。开会前,两两进行握手,问一共要握手多少次?
2.一个学习小组有15人。新年互送贺卡,若每两人之间互送一张,问一共可以送出贺卡多少张?
15×(15-1)÷2=105(次)
温馨提示:
数学思想方法可以h化繁为简、化难为易,
帮助我们解决问题。
小结:这节课你学到了什么?
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
拓展引申
(1)
3,9,11,17,20,_,_,36,41,…
+2 +3 +4 +5
(2)1,3,2,6,4,_,_,12,_,…
+3 + 3 +3 +3
×2 ×2 ×2 ×2
26
30
9
8
16
+6 +6 +6 +6
拓展引申
数字规律我最行
谢 谢
数学思考
师生握手:每2人握一次手,共握几次手?
怎么办呢?
握手实验或画点数数吧!
游戏挑战
学习目标
1.我能掌握“化繁为简、化难为易”的数学方法。
2.我能运用一定规律解决较复杂的数学问题。
3.提高归纳推理探索规律的能力。
并将两点连成一条线段
请同学们在纸上任意点上6个点
数一数你连成的线段有多少条
点数
增加 条数
总条 数
5个点连成线段的条数:1+2+3+4=10 (条)
6个点连成线段的条数:
8个点连成线段的条数:
12个点呢?20个点呢?请写出算式。
2
3
4
5
2
3
4
1
6
10
3
…
…
…
1+2+3+4+5=15 (条)
1+2+3+4+5+6+7=28(条)
1+2+3+4+5+6+7+8+9+10+11
1+2+3+4+5+6+…+18+19
2个点连成线段的条数:1(条)
3个点连成线段的条数:1+2=3(条)
4个点连成线段的条数:1+2+3=6(条)
我的发现
n个点:
1+2+3+…+(n-1)
用点连线的规律:
从1开始的前(n-1)个连续自然数的和
(即从1开始加起,一直加到比点数少1的连续几个自然数的和)
我找到规律啦!
n个点最多能连成多少条线段?
101个点最多能连成多少条线段?
1+2+3+4+5+6+7+…+100
= 5050(条)
1+2+3+4+5+6+7+…+(n-1)
= n(n-1) ÷ 2(条)
=(1+100)×100÷2
还有什么规律
考虑到重复的线段,会得到什么结论?
A
E
D
C
B
5
×
(5-1)
÷2
=10
5个点
点数×(点数-1)÷2 ,如果用n表示点数,这个规律可以表示为:
n (n-1) ÷ 2
师生(55人)握手:每2人握一次手,大家一共要握多少次手?
1+2+3+4+5+…+55=1540(次)
想一想:还有其它方法吗?
1.把下面的数列补充完整。
1,2,3,5,8,13,( )
3,6,10,15,21,( )
21
达标检测
2.摆一摆,找规律。
(1)第6个图形是什么图形?
(2)第7个图形需要用多少根小棒?第n个图形呢
(15根)
…
(2n+1根)
火眼金睛:我会辨
1.为迎接下五屯中心小学校园文化艺术节,节目筹备组15人到会议室开会。开会前,两两进行握手,问一共要握手多少次?
2.一个学习小组有15人。新年互送贺卡,若每两人之间互送一张,问一共可以送出贺卡多少张?
15×(15-1)÷2=105(次)
温馨提示:
数学思想方法可以h化繁为简、化难为易,
帮助我们解决问题。
小结:这节课你学到了什么?
多边形
边 数
3
4
5
6
内角和
180°
360°
540°
720°
(1)多边形内角和与它的边数有什么关系?
(2)一个九边形的内角和是多少度?
拓展引申
(1)
3,9,11,17,20,_,_,36,41,…
+2 +3 +4 +5
(2)1,3,2,6,4,_,_,12,_,…
+3 + 3 +3 +3
×2 ×2 ×2 ×2
26
30
9
8
16
+6 +6 +6 +6
拓展引申
数字规律我最行
谢 谢
