六年级数学下册课件-6.4 数学思考人教版(共21张PPT)
文档属性
| 名称 | 六年级数学下册课件-6.4 数学思考人教版(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
数学思考
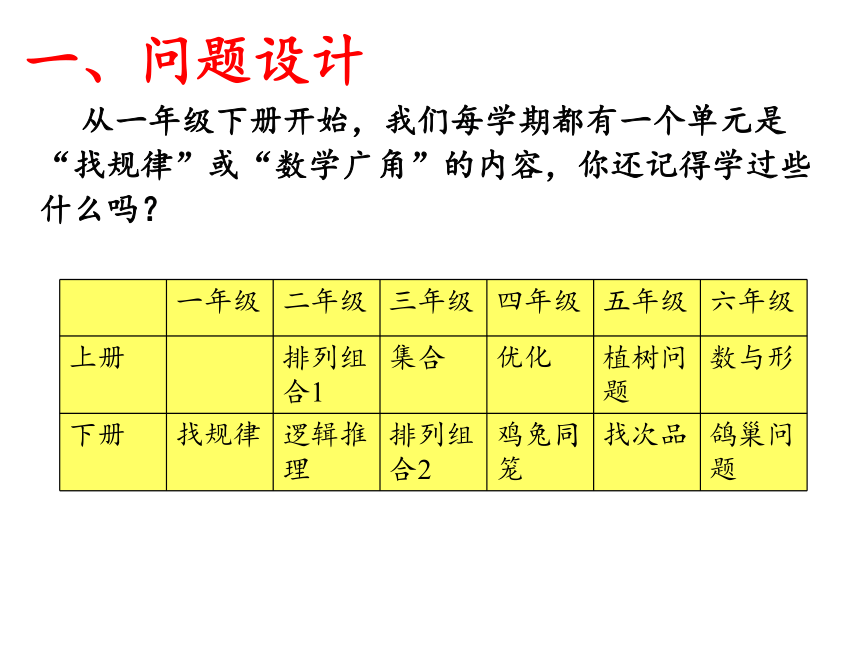
从一年级下册开始,我们每学期都有一个单元是“找规律”或“数学广角”的内容,你还记得学过些什么吗?
一年级 二年级 三年级 四年级 五年级 六年级
上册 排列组合1 集合 优化 植树问题 数与形
下册 找规律 逻辑推理 排列组合2 鸡兔同笼 找次品 鸽巢问题
一、问题设计
请你在纸上任意点上10个点,每2个点连成一条线段,一共能连成多少条线段?
一、问题设计
(五点连线)
(三点连线)
(两点连线)
(六点连线)
(七点连线)
(四点连线)
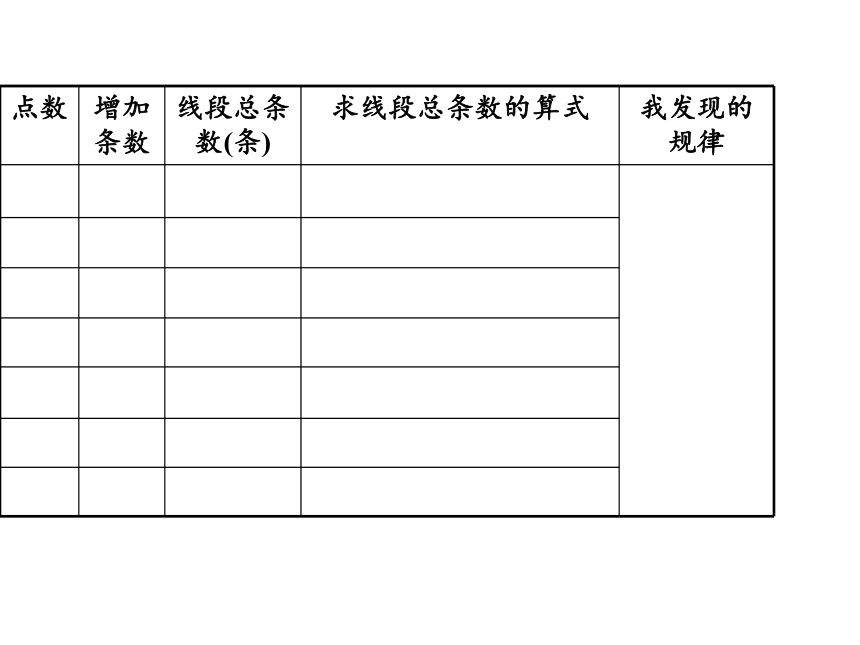
1、小组合作:先连,后填表。
二、互动设计
点数 增加条数 线段总条数(条) 求线段总条数的算式 我发现的规律
2、小组讨论:
(1)仔细观察,每次增加的线段条数和点数有什么关系?
(2)怎样根据点数求线段总数?有什么规律?
小组学习任务
2
A
B
1
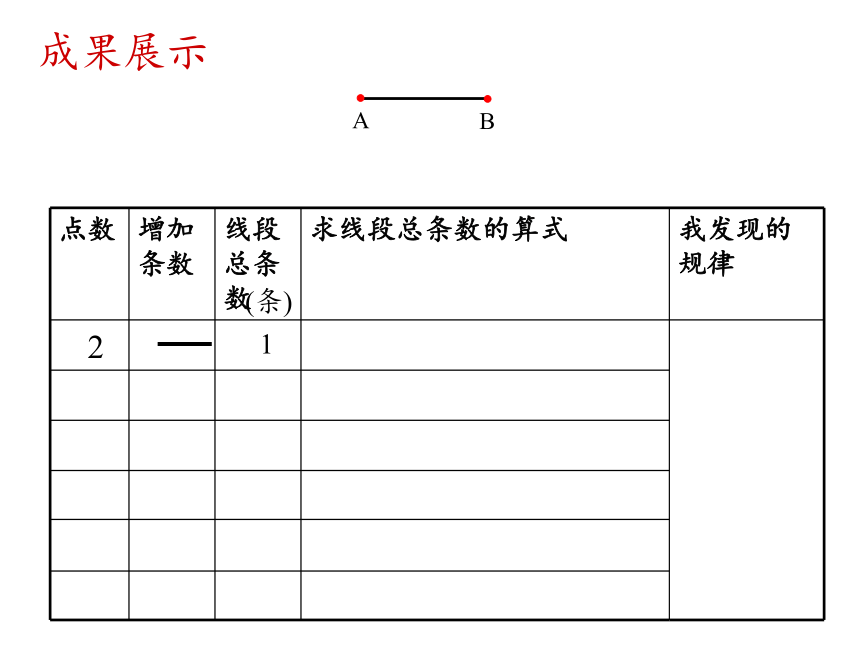
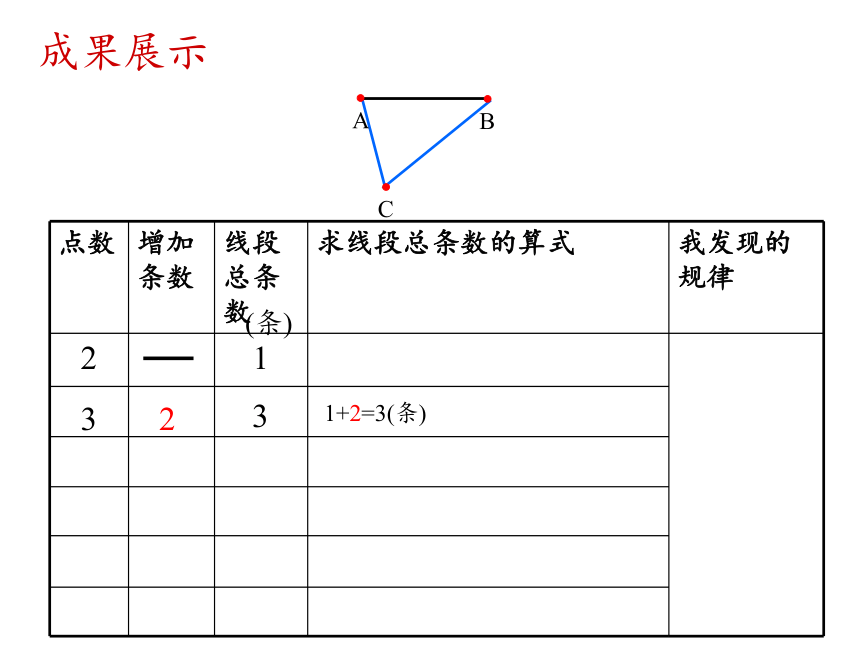
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
(条)
3
C
A
B
1+2=3(条)
2
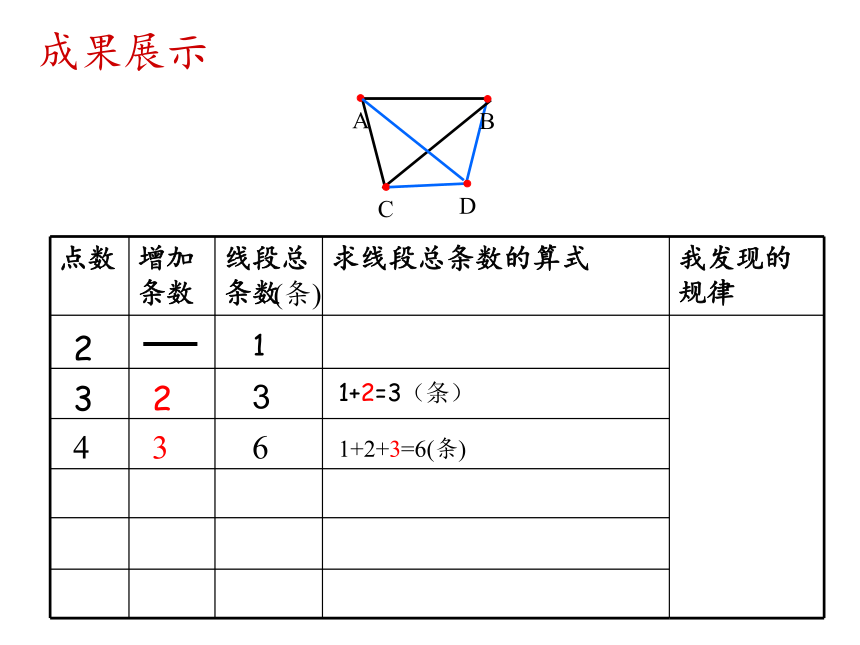
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
2 1
3
(条)
C
A
B
D
4
1+2+3=6(条)
3
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
2
1
3
1+2=3(条)
2
3
6
(条)
C
B
D
5
E
A
1+2+3+4=10(条)
4
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
10
2
1
3
1+2=3(条)
2
4
1+2+3=6(条)
3
3
6
(条)
C
D
6
A
B
E
F
1+2+3+4+5=15(条)
5
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
5
1+2+3+4=10(条)
4
2
1
3
1+2=3(条)
2
4
1+2+3=6(条)
3
15
3
10
6
(条)
7
C
D
E
F
1+2+3+4+5+6=21(条)
6
B
A
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
G
21
(条)
5
4
2
1
3
2
4
3
5
6
3
6
10
15
1+2+3+4=10(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4+5=15(条)
成果展示
5
4
2
1
3
2
4
3
5
6
1+2+3+4=10(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4+5=15(条)
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
… 7
1+2+3+4+5+6=21(条)
6
3
6
10
15
21
n
n-1
1+2+3+4+……+(n-1)
2
n (n-1)
点数是几,就从1开始,依次加到点数减1的那个数,所得的和就是总线段数。
(条)
请你在纸上任意点上10个点,每2个点连成一条线段,一共能连成多少条线段?
一、问题设计
1+2+3+……+8+9=
45(条)
根据规律,你知道12个点、20个点能连成多少条线段吗?请写出算式
12个点:
20个点:
1+2+3+……+10+11=66(条)
1+2+3+……+18+19=190(条)
三、达标练习设计
图中共有( )条线段。
10
1+2+3+4=10(条)
从大安北到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同的车票?
1+2+3+4+5+6+7+8+9=
8+2=10(个)
45(种)
答:要准备45种不同车票。
三、达标练习设计
完成教材103页的第2题。
三、达标练习设计
拓展延伸
……
1、摆n个八边形需要( )根小棒。
2、用2017根小棒可以摆( )个八边形。
7n+1
288
(2017-1) ÷7=288(个)
数学家华罗庚说过:“同学们,在解决数学难题时,我们要学会知难而“退”。要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。”
谢 谢
数学思考
从一年级下册开始,我们每学期都有一个单元是“找规律”或“数学广角”的内容,你还记得学过些什么吗?
一年级 二年级 三年级 四年级 五年级 六年级
上册 排列组合1 集合 优化 植树问题 数与形
下册 找规律 逻辑推理 排列组合2 鸡兔同笼 找次品 鸽巢问题
一、问题设计
请你在纸上任意点上10个点,每2个点连成一条线段,一共能连成多少条线段?
一、问题设计
(五点连线)
(三点连线)
(两点连线)
(六点连线)
(七点连线)
(四点连线)
1、小组合作:先连,后填表。
二、互动设计
点数 增加条数 线段总条数(条) 求线段总条数的算式 我发现的规律
2、小组讨论:
(1)仔细观察,每次增加的线段条数和点数有什么关系?
(2)怎样根据点数求线段总数?有什么规律?
小组学习任务
2
A
B
1
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
(条)
3
C
A
B
1+2=3(条)
2
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
2 1
3
(条)
C
A
B
D
4
1+2+3=6(条)
3
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
2
1
3
1+2=3(条)
2
3
6
(条)
C
B
D
5
E
A
1+2+3+4=10(条)
4
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
10
2
1
3
1+2=3(条)
2
4
1+2+3=6(条)
3
3
6
(条)
C
D
6
A
B
E
F
1+2+3+4+5=15(条)
5
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
5
1+2+3+4=10(条)
4
2
1
3
1+2=3(条)
2
4
1+2+3=6(条)
3
15
3
10
6
(条)
7
C
D
E
F
1+2+3+4+5+6=21(条)
6
B
A
成果展示
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
G
21
(条)
5
4
2
1
3
2
4
3
5
6
3
6
10
15
1+2+3+4=10(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4+5=15(条)
成果展示
5
4
2
1
3
2
4
3
5
6
1+2+3+4=10(条)
1+2=3(条)
1+2+3=6(条)
1+2+3+4+5=15(条)
点数 增加条数 线段总条数 求线段总条数的算式 我发现的规律
… 7
1+2+3+4+5+6=21(条)
6
3
6
10
15
21
n
n-1
1+2+3+4+……+(n-1)
2
n (n-1)
点数是几,就从1开始,依次加到点数减1的那个数,所得的和就是总线段数。
(条)
请你在纸上任意点上10个点,每2个点连成一条线段,一共能连成多少条线段?
一、问题设计
1+2+3+……+8+9=
45(条)
根据规律,你知道12个点、20个点能连成多少条线段吗?请写出算式
12个点:
20个点:
1+2+3+……+10+11=66(条)
1+2+3+……+18+19=190(条)
三、达标练习设计
图中共有( )条线段。
10
1+2+3+4=10(条)
从大安北到北京的某次快车中途要停靠8个大站,铁路局要为这次快车准备多少种不同的车票?
1+2+3+4+5+6+7+8+9=
8+2=10(个)
45(种)
答:要准备45种不同车票。
三、达标练习设计
完成教材103页的第2题。
三、达标练习设计
拓展延伸
……
1、摆n个八边形需要( )根小棒。
2、用2017根小棒可以摆( )个八边形。
7n+1
288
(2017-1) ÷7=288(个)
数学家华罗庚说过:“同学们,在解决数学难题时,我们要学会知难而“退”。要善于退,足够的退,退到最简单又不失关键的地方。那么,你就已经找到这道题的精髓了。”
谢 谢
