苏教版六年级数学下册7.1.11式与方程 课件 (共21张PPT)
文档属性
| 名称 | 苏教版六年级数学下册7.1.11式与方程 课件 (共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 16:43:19 | ||
图片预览







文档简介
(共21张PPT)
总复习
《式与方程》
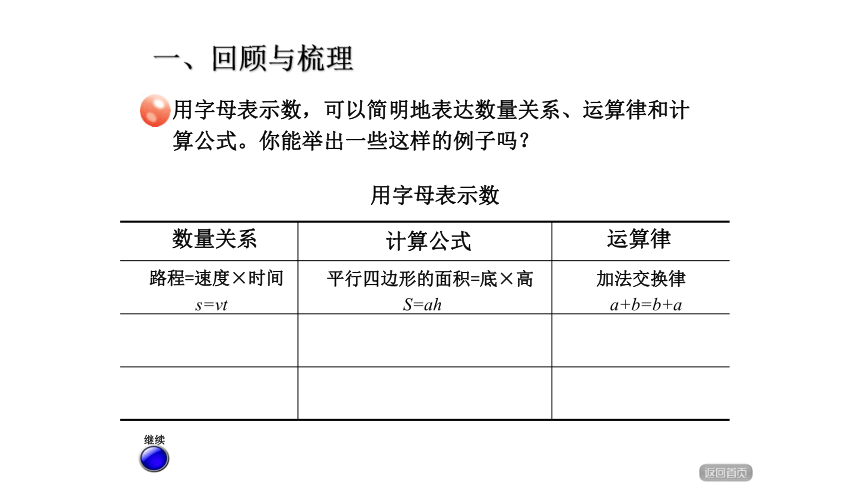
一、回顾与梳理
用字母表示数,可以简明地表达数量关系、运算律和计算公式。你能举出一些这样的例子吗?
数量关系
计算公式
运算律
s=vt
用字母表示数
S=ah
a+b=b+a
继续
路程=速度×时间
平行四边形的面积=底×高
加法交换律
练习
用含有字母的式子表示下面的数量
1、小敏原有a本故事书,捐献给灾区小朋友5本后,还剩( )本。
2、一辆公共汽车每小时行b千米,3小时共行( )千米。
3、一种贺卡的单价是a元,小英买5张这样的贺卡,用去( )元;
小明买5张这样的贺卡,付出10元,应找回( )元。
4、苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付( )元。
5、一个正方形的边长是a米,周长是 ( )米,面积是( )平方米。当a=3时,正方形的周长是( )米,面积是( )平方米。
5a
10-5a
a-5
3b
6.2a+4.5b
4a
a2
12
9
温馨提醒:
①在含有字母的式子里,数和字母中间的乘号 可以作“ ”,也可以省略不写。
②数字与字母相乘省略乘号时,一般把数写在字母的前面
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
④1和字母相乘,1省略不写。
(1) X+56 ( )
说出下面哪些是等式?哪些是方程?
(2)0.12M=24 ( )
(3)12×1.3=15.6 ( )
(4) ab=0 ( )
(5) X-2.5<11 ( )
(6) 6Y=0.12 ( )
(7) H+0.45>1 ( )
(8) 16+4X=0 ( )
√
√
√
√
√
表示相等的式子叫等式。
含有未知数的等式叫方程。
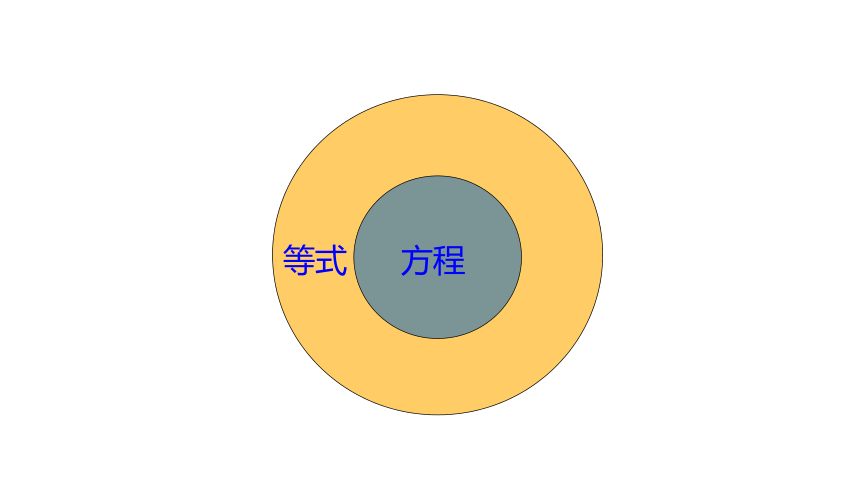
等式与方程有什么联系和区别?
方程一定是等式但等式不一定是方程。
等式
方程
等式的性质:
1.等式的两边同时加上(减去)同一个数,等式仍然成立。
2.等式的两边同时乘(除以)同一个数(0除外),等式仍然成立。
解方程
16+4χ = 40
30χ = 15
χ+3 = 15
χ- χ=
解方程
30χ = 15
16+4χ = 40
解:
30χ÷30 = 15÷30
16+4χ-16 = 40-16
χ= 0.5
4χ= 24
4χ÷4= 24÷4
解:
χ= 6
χ+3 = 15
χ+3-3 = 15-3
χ = 12
χ- χ=
解:
解:
( ) χ=
χ=
χ =
交流:
说一说列方程解应用题的步 骤。你认为哪一步最关键?
一般分5步:
1)根据题意,解设未知数为x .
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
现在能收看56
套电视节目。
比开通有线电视前的5倍少4套。
开通有线电视前只能收看多少套电视节目?
解:设开通有线电视前只能收看x套电视节目。
5x -4= 56
5x = 60
x = 12
答:开通有线电视前只能收看12套电视节目。
开通前收看套数×5-4=现在收看56套
填空
(1)学校原有图书7160本,又买来a本,现在共有图书( )本。
(2)有m吨煤,每次运6吨,需运( )次。
(3)每米花布13.6元,X米需要( )元。
( 4 )每小时行b千米,3小时行( )千米,7小时行( )千米。
7160+a
m÷6
13.6X
3b
7b
判断
(1)含有未知数的式子叫方程………… ( )
(2)n表示自然数,2n就可以表示偶数 ( )
(3)因为22=2×2,所以a2=a×2…… ( )
(4)56-X<0.7不是方程…………… ( )
(5)c +c=2c,a×a=2a。…………… ( )
×
√
×
√
×
a2表示2个a相乘
(6)所有的等式都是方程………… ( )
(7)5×b 可以记作b5 ………… ( )
(8)2a和a2的意义相同 …… ( )
(9)0.5X=0.7是方程不是等式…………… ( )
(10)方程的解和解方程是一样的……… ( )
×
×
×
×
×
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系
是:b=2a -10(b表示码数,a表示厘米数)。根据这个关系,
把下表填写完整。
18
23.5
40
b=2a -10(b表示码数,a表示厘米数)
2a-10=b
18×2-10
=36-10
=26
2a-10=b
23.5×2-10
=47-10
=37
2a-10=b
2a-10=40
2a=50
a=25
23.5
18
40
26
37
25
本节课我们复习了哪些式与方程的相关知识?
总复习
《式与方程》
一、回顾与梳理
用字母表示数,可以简明地表达数量关系、运算律和计算公式。你能举出一些这样的例子吗?
数量关系
计算公式
运算律
s=vt
用字母表示数
S=ah
a+b=b+a
继续
路程=速度×时间
平行四边形的面积=底×高
加法交换律
练习
用含有字母的式子表示下面的数量
1、小敏原有a本故事书,捐献给灾区小朋友5本后,还剩( )本。
2、一辆公共汽车每小时行b千米,3小时共行( )千米。
3、一种贺卡的单价是a元,小英买5张这样的贺卡,用去( )元;
小明买5张这样的贺卡,付出10元,应找回( )元。
4、苹果的单价是6.2元/千克,梨的单价是4.5元/千克。妈妈买了a千克苹果和b千克梨,一共要付( )元。
5、一个正方形的边长是a米,周长是 ( )米,面积是( )平方米。当a=3时,正方形的周长是( )米,面积是( )平方米。
5a
10-5a
a-5
3b
6.2a+4.5b
4a
a2
12
9
温馨提醒:
①在含有字母的式子里,数和字母中间的乘号 可以作“ ”,也可以省略不写。
②数字与字母相乘省略乘号时,一般把数写在字母的前面
③数与数之间的乘号不能省略。加号、减号、除号都不能省略。
④1和字母相乘,1省略不写。
(1) X+56 ( )
说出下面哪些是等式?哪些是方程?
(2)0.12M=24 ( )
(3)12×1.3=15.6 ( )
(4) ab=0 ( )
(5) X-2.5<11 ( )
(6) 6Y=0.12 ( )
(7) H+0.45>1 ( )
(8) 16+4X=0 ( )
√
√
√
√
√
表示相等的式子叫等式。
含有未知数的等式叫方程。
等式与方程有什么联系和区别?
方程一定是等式但等式不一定是方程。
等式
方程
等式的性质:
1.等式的两边同时加上(减去)同一个数,等式仍然成立。
2.等式的两边同时乘(除以)同一个数(0除外),等式仍然成立。
解方程
16+4χ = 40
30χ = 15
χ+3 = 15
χ- χ=
解方程
30χ = 15
16+4χ = 40
解:
30χ÷30 = 15÷30
16+4χ-16 = 40-16
χ= 0.5
4χ= 24
4χ÷4= 24÷4
解:
χ= 6
χ+3 = 15
χ+3-3 = 15-3
χ = 12
χ- χ=
解:
解:
( ) χ=
χ=
χ =
交流:
说一说列方程解应用题的步 骤。你认为哪一步最关键?
一般分5步:
1)根据题意,解设未知数为x .
2)找出具体的数量,列出等量关系式。
3)根据等量关系式,列出方程。
4)解方程
5)检验并答句。
现在能收看56
套电视节目。
比开通有线电视前的5倍少4套。
开通有线电视前只能收看多少套电视节目?
解:设开通有线电视前只能收看x套电视节目。
5x -4= 56
5x = 60
x = 12
答:开通有线电视前只能收看12套电视节目。
开通前收看套数×5-4=现在收看56套
填空
(1)学校原有图书7160本,又买来a本,现在共有图书( )本。
(2)有m吨煤,每次运6吨,需运( )次。
(3)每米花布13.6元,X米需要( )元。
( 4 )每小时行b千米,3小时行( )千米,7小时行( )千米。
7160+a
m÷6
13.6X
3b
7b
判断
(1)含有未知数的式子叫方程………… ( )
(2)n表示自然数,2n就可以表示偶数 ( )
(3)因为22=2×2,所以a2=a×2…… ( )
(4)56-X<0.7不是方程…………… ( )
(5)c +c=2c,a×a=2a。…………… ( )
×
√
×
√
×
a2表示2个a相乘
(6)所有的等式都是方程………… ( )
(7)5×b 可以记作b5 ………… ( )
(8)2a和a2的意义相同 …… ( )
(9)0.5X=0.7是方程不是等式…………… ( )
(10)方程的解和解方程是一样的……… ( )
×
×
×
×
×
使方程左右两边相等的未知数的值叫作方程的解。
求方程的解的过程叫作解方程。
鞋的尺码通常用“码”或“厘米”作单位,它们之间的关系
是:b=2a -10(b表示码数,a表示厘米数)。根据这个关系,
把下表填写完整。
18
23.5
40
b=2a -10(b表示码数,a表示厘米数)
2a-10=b
18×2-10
=36-10
=26
2a-10=b
23.5×2-10
=47-10
=37
2a-10=b
2a-10=40
2a=50
a=25
23.5
18
40
26
37
25
本节课我们复习了哪些式与方程的相关知识?
