2021-2022学年九年级数学苏科版下册第6章图形的相似单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学苏科版下册第6章图形的相似单元测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 215.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 23:38:30 | ||
图片预览



文档简介
《第6章 图形的相似》单元测试卷
一.选择题
1.如图,梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7 B.5:7 C.3:7 D.2:5
2已知线段a、b、c,其中c是a、b的比例中项,若a=9,b=4,则c长( )
A.18 B.5 C.6 D.±6
3.若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )
A.1 B.3 C. D.1或3
4.(2020 灌云县模拟)如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
5.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部 B.只能选在原图形的内部
C.只能选在原图形的边上 D.可以选择任意位置
6.在同一时刻,一竹竿高2m,影长3m,而一大楼的影长是45m,这个大楼的高是( )
A.15m B.67.5m C.20m D.30m
7.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4 B.4﹣4
C.﹣4+4 D.4﹣4或﹣4+4
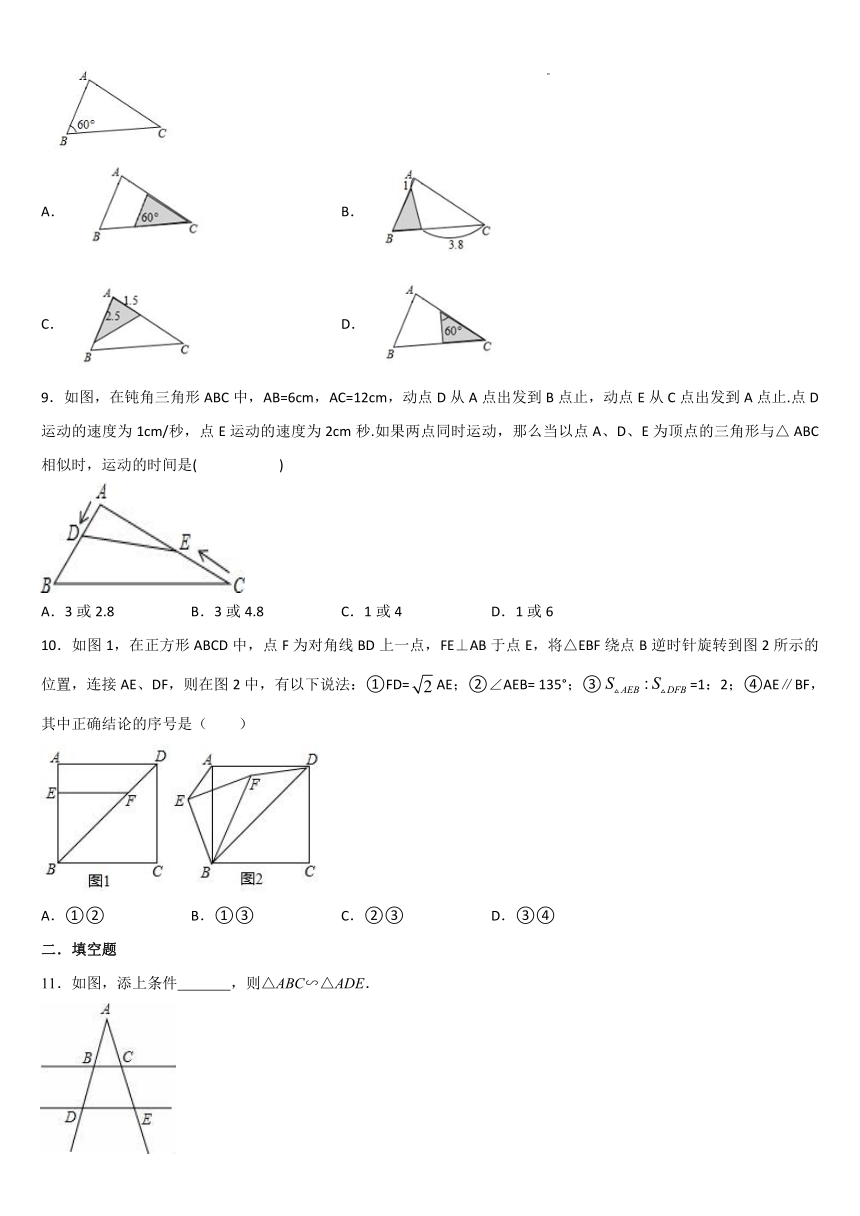
8.如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
9.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ ABC相似时,运动的时间是( )
A.3或2.8 B.3或4.8 C.1或4 D.1或6
10.如图1,在正方形ABCD中,点F为对角线BD上一点,FE⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE、DF,则在图2中,有以下说法:①FD=AE;②∠AEB= 135°;③=1:2;④AE∥BF,其中正确结论的序号是( )
A.①② B.①③ C.②③ D.③④
二.填空题
11.如图,添上条件 ,则△ABC∽△ADE.
12.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC= cm,CG= cm.
13.若线段AB上黄金分割点为C,且AC<BC,又AB的长为4cm,则CB的长为 cm.
14.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD= ,AC= .
15.已知坐标平面内,△ABC的各顶点坐标分别是A(0,1),B(2,﹣3),C(﹣2,0),△DEF各顶点坐标分别是D(0,2),E(4,﹣6),F(﹣4,0),则△ABC与△DEF的面积之比为 .
16.四个全等的直角三角形如图摆放成一个风车的形状,形成正方形ABCD和正方形IJKL.若BF平分∠ABK,AF:FK=5:3,风车周长为10+6,则四个直角三角形的面积和是___.
17.如图,在等边三角形中,点D,E分别在边上,把沿着翻折,使点A恰好落在边上的点P处.若的周长为4,的周长为5,则的值为________.
18.如图所示,在△ABC中,AB=8cm,BC=16 cm.点P从点A出发沿AB向点B以2 cm/s的速度运动,点Q从点B出发沿BC向点C以4 cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则_____________秒钟后△PBQ与△ABC相似?
三.解答题
19.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
20.已知==,求的值.
21如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
22.如图,已知=,试说明OB OD=OC OE.
23.如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究:
由于AB∥CD,得出S△ACD=S△CBD;同理S△CED=S△CFD;
所以===;
因为AC=CE,所以BD=DF.
(1)如果AD∥CF,你发现AC、CE、BD、DF之间存在怎样的关系并说明你的猜想的正确性;
(2)利用你发现的结论,请你通过画图把已知线段MN分成2:3两部分.
D2.C 3.A 4.C 5.D 6.D 7.B 8.C 9.B 10B
11.解:∵∠A=∠A∴当BC∥DE或∠ABC=∠ADE或时,△ABC∽△ADE.
12.6,2.5.
13.2﹣2.
14.5.
16.9
17.
18.0.8或2
19.(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF﹣PA=PD﹣PA=﹣1,
DM=AD﹣AM=2﹣(﹣1)=3﹣;
(2)证明:∵AM2=(﹣1)2=6﹣2,AD DM=2(3﹣)=6﹣2,
∴AM2=AD DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD DM,
∴═=,
∴点M是AD的黄金分割点.
20.DF=.
解:在Rt△ACB中,∵AB=2,BC=2,∠ACB=90°,
∴AC==4,
∵AD=DB,
∴CD=DA=DB=,
∴∠DCA=∠A,
∵∠CDB=∠CDE,∠FDE=∠FDA,
∴∠CDF=90°,
∴∠CDF=∠ACB,
∴△CDF∽△ACB,
∴=,
∴=,
∴DF=
21.(1),,;(2)是直角三角形.
解:(1)∵,
∴.
设,
则解得
又∵,
∴,解得.
∴,,.
(2)∵,
∴是直角三角形.
23.解:(1)两条直线被平行线所截,对应线段成比例.即:AC:CE=BD:DF.
(2)为了把MN分成2:3两部分,从M点出发作一条射线MT,与MN有适当的夹角.
MT上取AB两点.使MA=2单位,MB=5单位,(即MA:AB=2:3).
连接NB.过A作NB的平行线,与MN相交于P.则MP:PN=2:3.
一.选择题
1.如图,梯形ABCD中,AB∥CD∥EF,若AB=10,CD=3,EF=5,则CF:FB等于( )
A.2:7 B.5:7 C.3:7 D.2:5
2已知线段a、b、c,其中c是a、b的比例中项,若a=9,b=4,则c长( )
A.18 B.5 C.6 D.±6
3.若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )
A.1 B.3 C. D.1或3
4.(2020 灌云县模拟)如图,已知在△ABC中,P为AB上一点,连接CP,以下条件中不能判定△ACP∽△ABC的是( )
A.∠ACP=∠B B.∠APC=∠ACB C. D.
5.用作位似形的方法,可以将一个图形放大或缩小,位似中心( )
A.只能选在原图形的外部 B.只能选在原图形的内部
C.只能选在原图形的边上 D.可以选择任意位置
6.在同一时刻,一竹竿高2m,影长3m,而一大楼的影长是45m,这个大楼的高是( )
A.15m B.67.5m C.20m D.30m
7.如图,在△ABC中,AB=AC=8,∠A=36°,BD平分∠ABC交AC于点D,则AD=( )
A.4 B.4﹣4
C.﹣4+4 D.4﹣4或﹣4+4
8.如图,在中,,,,将沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.
C. D.
9.如图,在钝角三角形ABC中,AB=6cm,AC=12cm,动点D从A点出发到B点止,动点E从C点出发到A点止.点D运动的速度为1cm/秒,点E运动的速度为2cm秒.如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ ABC相似时,运动的时间是( )
A.3或2.8 B.3或4.8 C.1或4 D.1或6
10.如图1,在正方形ABCD中,点F为对角线BD上一点,FE⊥AB于点E,将△EBF绕点B逆时针旋转到图2所示的位置,连接AE、DF,则在图2中,有以下说法:①FD=AE;②∠AEB= 135°;③=1:2;④AE∥BF,其中正确结论的序号是( )
A.①② B.①③ C.②③ D.③④
二.填空题
11.如图,添上条件 ,则△ABC∽△ADE.
12.如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,AG=5cm,则BC= cm,CG= cm.
13.若线段AB上黄金分割点为C,且AC<BC,又AB的长为4cm,则CB的长为 cm.
14.在Rt△ABC中,AD是斜边上的高,若AB=,DC=2,则BD= ,AC= .
15.已知坐标平面内,△ABC的各顶点坐标分别是A(0,1),B(2,﹣3),C(﹣2,0),△DEF各顶点坐标分别是D(0,2),E(4,﹣6),F(﹣4,0),则△ABC与△DEF的面积之比为 .
16.四个全等的直角三角形如图摆放成一个风车的形状,形成正方形ABCD和正方形IJKL.若BF平分∠ABK,AF:FK=5:3,风车周长为10+6,则四个直角三角形的面积和是___.
17.如图,在等边三角形中,点D,E分别在边上,把沿着翻折,使点A恰好落在边上的点P处.若的周长为4,的周长为5,则的值为________.
18.如图所示,在△ABC中,AB=8cm,BC=16 cm.点P从点A出发沿AB向点B以2 cm/s的速度运动,点Q从点B出发沿BC向点C以4 cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则_____________秒钟后△PBQ与△ABC相似?
三.解答题
19.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.
(1)求AM,DM的长;
(2)求证:AM2=AD DM;
(3)根据(2)的结论你能找出图中的黄金分割点吗?
20.已知==,求的值.
21如图,AD是△ABC的中线,P是AD的中点,延长BP交AC于点F.
(1)试说明PB=3PF;
(2)若AC的长为12,求AF的长.
22.如图,已知=,试说明OB OD=OC OE.
23.如图所示,已知AB∥CD∥EF,AC=CE,某同学在探索DB与DF的关系时,进行了下列探究:
由于AB∥CD,得出S△ACD=S△CBD;同理S△CED=S△CFD;
所以===;
因为AC=CE,所以BD=DF.
(1)如果AD∥CF,你发现AC、CE、BD、DF之间存在怎样的关系并说明你的猜想的正确性;
(2)利用你发现的结论,请你通过画图把已知线段MN分成2:3两部分.
D2.C 3.A 4.C 5.D 6.D 7.B 8.C 9.B 10B
11.解:∵∠A=∠A∴当BC∥DE或∠ABC=∠ADE或时,△ABC∽△ADE.
12.6,2.5.
13.2﹣2.
14.5.
16.9
17.
18.0.8或2
19.(1)解:在Rt△APD中,PA=AB=1,AD=2,
∴PD==,
∴AM=AF=PF﹣PA=PD﹣PA=﹣1,
DM=AD﹣AM=2﹣(﹣1)=3﹣;
(2)证明:∵AM2=(﹣1)2=6﹣2,AD DM=2(3﹣)=6﹣2,
∴AM2=AD DM;
(3)点M是AD的黄金分割点.理由如下:
∵AM2=AD DM,
∴═=,
∴点M是AD的黄金分割点.
20.DF=.
解:在Rt△ACB中,∵AB=2,BC=2,∠ACB=90°,
∴AC==4,
∵AD=DB,
∴CD=DA=DB=,
∴∠DCA=∠A,
∵∠CDB=∠CDE,∠FDE=∠FDA,
∴∠CDF=90°,
∴∠CDF=∠ACB,
∴△CDF∽△ACB,
∴=,
∴=,
∴DF=
21.(1),,;(2)是直角三角形.
解:(1)∵,
∴.
设,
则解得
又∵,
∴,解得.
∴,,.
(2)∵,
∴是直角三角形.
23.解:(1)两条直线被平行线所截,对应线段成比例.即:AC:CE=BD:DF.
(2)为了把MN分成2:3两部分,从M点出发作一条射线MT,与MN有适当的夹角.
MT上取AB两点.使MA=2单位,MB=5单位,(即MA:AB=2:3).
连接NB.过A作NB的平行线,与MN相交于P.则MP:PN=2:3.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
