2021-2022学年苏科版数学九年级下册6.4探索三角形相似的条件课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级下册6.4探索三角形相似的条件课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 521.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 23:44:56 | ||
图片预览


文档简介
探索三角形相似的条件
一、单选题
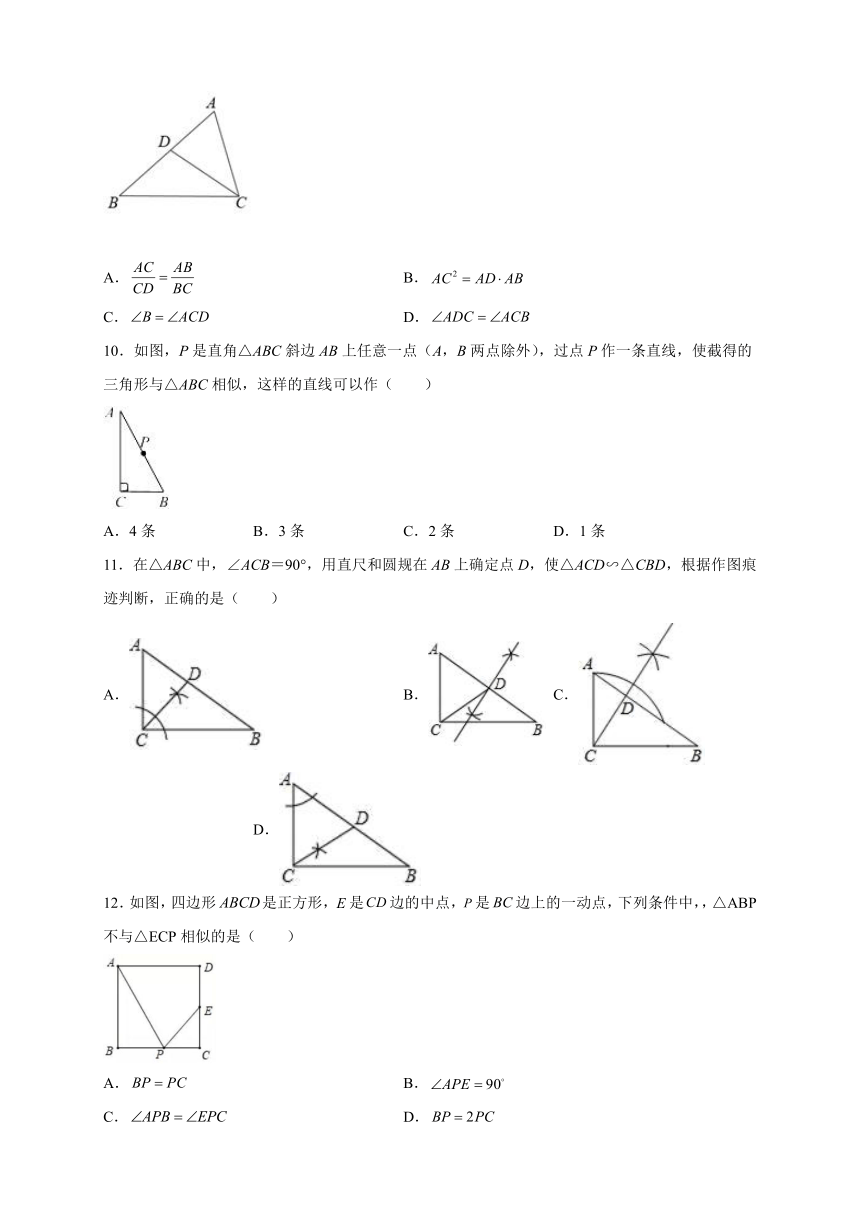
1.如图,在三角形纸片ABC中,,,,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.如图,甲、乙中各有两个三角形,其边长和角的度数如图上标注,则对甲、乙中两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有甲中两个三角形相似 D.只有乙中两个三角形相似
3.如图,下列不能判定与相似的是( )
A. B. C. D.
4.下列说法,其中正确的有( )
①各有一个角是60°的两个等腰三角形相似;
②各有一个角是80°的两个等腰三角形相似;
③各有一个角是100°的两个等腰三角形相似;
④两边成比例的两个等腰三角形相似.
A.1个 B.2个 C.3个 D.4个
5.如图,是平行四边形ABCD的对角线BD上一点,AM的延长线交BC于点,交DC的延长线于点,图中相似三角形有( )
A.6对 B.5对 C.4对 D.3对
6.如图,,,AE、FD分别交BC于点G、H,则图中的相似三角形共有( )
A.3对 B.4对 C.5对 D.6对
7.如图,在△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
8.如图,和中,,则添加下列条件后无法判定的是( )
A. B. C. D.
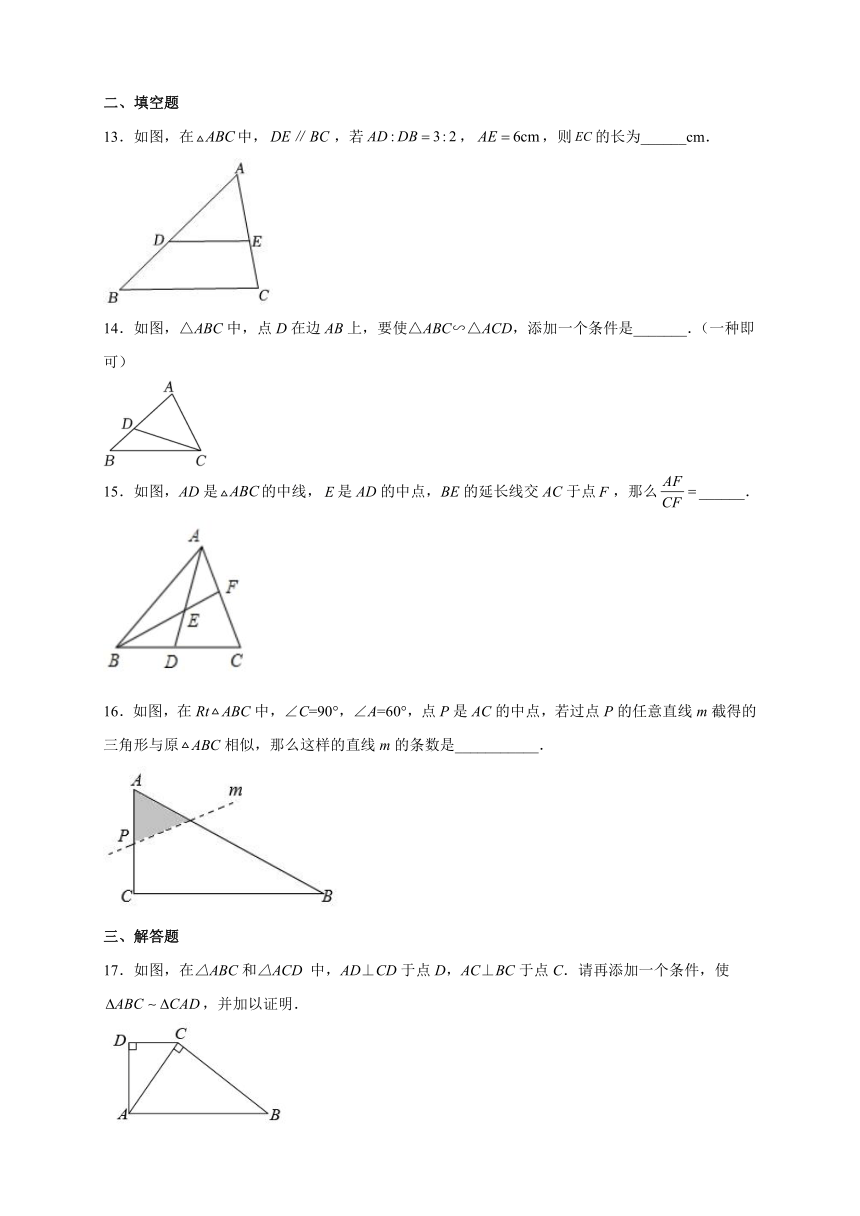
9.如图, 已知在 中, 点 在边 上, 那么下列条件中 不能判定 的是( )
A. B.
C. D.
10.如图,P是直角△ABC斜边AB上任意一点(A,B两点除外),过点P作一条直线,使截得的三角形与△ABC相似,这样的直线可以作( )
A.4条 B.3条 C.2条 D.1条
11.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )
A. B. C. D.
12.如图,四边形是正方形,是边的中点,是边上的一动点,下列条件中,,△ABP不与△ECP相似的是( )
A. B.
C. D.
二、填空题
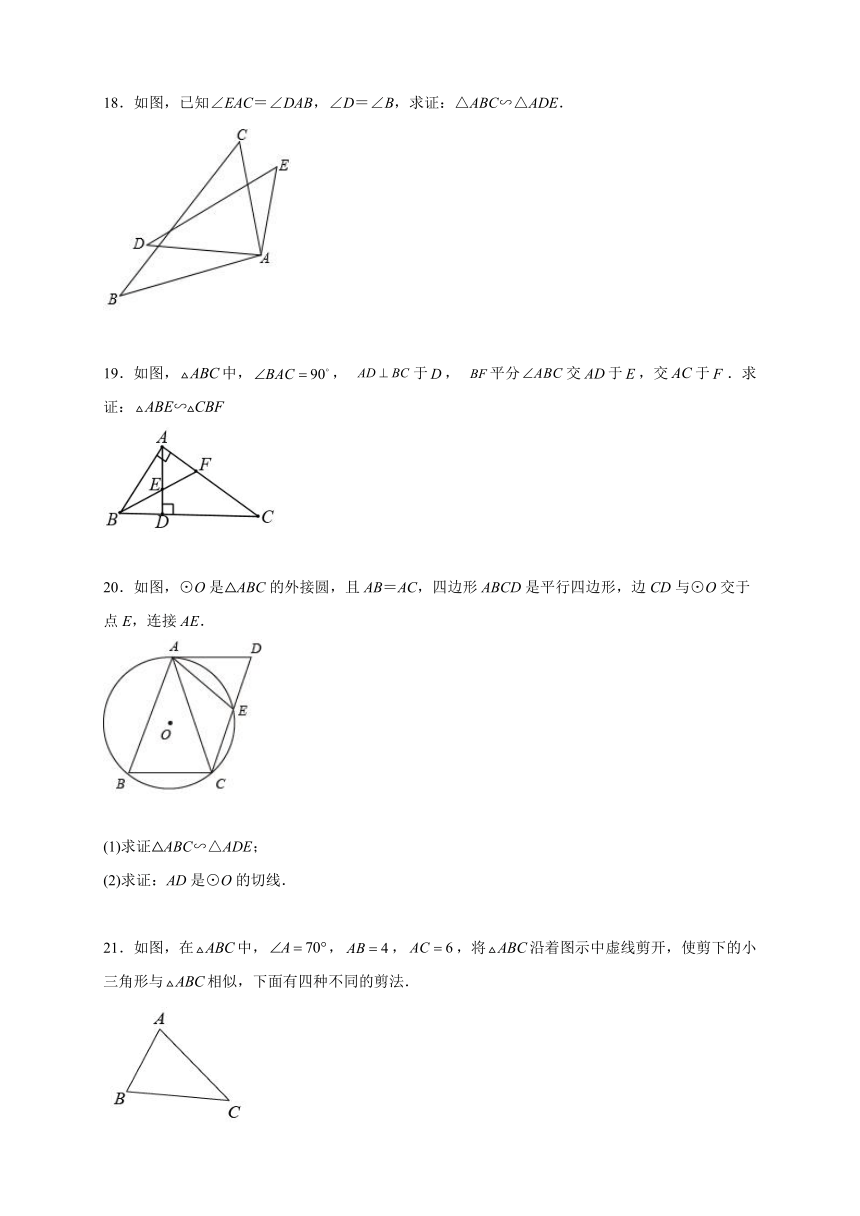
13.如图,在中,,若,,则的长为______cm.
14.如图,△ABC中,点D在边AB上,要使△ABC∽△ACD,添加一个条件是_______.(一种即可)
15.如图,AD是的中线,是AD的中点,BE的延长线交AC于点,那么______.
16.如图,在RtABC中,∠C=90°,∠A=60°,点P是AC的中点,若过点P的任意直线m截得的三角形与原ABC相似,那么这样的直线m的条数是___________.
三、解答题
17.如图,在△ABC和△ACD 中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使,并加以证明.
18.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
19.如图,中,, 于, 平分交于,交于.求证:
20.如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证△ABC∽△ADE;
(2)求证:AD是⊙O的切线.
21.如图,在中,,,,将沿着图示中虚线剪开,使剪下的小三角形与相似,下面有四种不同的剪法.
(1)请选择其中一种正确的剪法______(填序号);
(2)写出所选剪法中两个三角形相似的证明过程.
试卷第1页,共3页
参考答案:
1.B
解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为 ,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为 ,对应边,即:,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
2.C
解:∵甲中两个三角形的两个内角分别为75°、35°和70°、75°,
∴两个三角形的另一个内角的度数分别为70°和35°,
∴两个三角形的三个内角分别对应相等,
∴甲中两个三角形相似,
∵,
∴乙中两个三角形不相似,
∴只有甲中两个三角形相似,
故选:C.
3.A
解:虽然,但∠ABD≠∠C,
∴△ABD与△ACB不相似,
∴选项A符合;
∵,∠A=∠A,
∴△ABD∽△ACB,
∴选项B不符合;
∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴选项C不符合;
∵∠ADB=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴选项D不符合.
故选:A.
4.B
解:各有一个角是60°的两个等腰三角形都为等边三角形,它们相似,所以①正确;
顶角为80度的等腰三角形与底角为80度的等腰三角形不相似,所以②错误;
各有一个角是100°的两个等腰三角形的底角都为40度,它们相似,所以③正确;
两边成比例的两个等腰三角形不相似,所以④错误.
故选B.
5.A
解:∵四边形ABCD是平行四边形,
∴ , , ,
∵,
∴ ,
∵,
∴
∴,
则图中相似三角形有6对,它们分别是:,,,
故选:A.
6.D
解:∵,,
∴△BFH∽△BAG,
△BAG∽△CEG,
△BFH∽△CEG,
△BFH∽△CDH,
△CEG∽△CDH,
△CDH∽△BAG.
∴相似三角形共有6对.
故选C.
7.C
解:如图1,过点作于点,
,
,
,
,
,
在和中,,但或者,但,
则与不相似;
如图2,,
,
在和中,,
;
如图3和图4,剪下的阴影三角形均与有一组公共角,还有一组大小均为的相等的角,
所以图3和图4中,剪下的阴影三角形均与相似;
综上,满足剪下的阴影三角形与相似的个数是3个,
故选:C.
8.D
解:∵,,
∴ ,
故选项A不符合题意;
∵,,
∴,
故选项B不符合题意;
∵,,
∴,
故选项C不符合题意;
∵,但不一定相等,
∴不一定相似,
则添加条件后无法判定;
故选项D符合题意.
故选D.
9.A
解:而不一定相等,不能判断,故A符合题意;
,
而
故B不符合题意;
,
故C不符合题意;
,
故D不符合题意;
故选A
10.B
解:如图,过点P可作PE∥BC或PE″∥AC,
∴△APE∽△ABC、△PBE″∽△ABC;
过点P还可作PE′⊥AB,可得:∠EPA=∠C=90°,∠A=∠A
∴△APE∽△ACB;
∴满足这样条件的直线的作法共有3种.
故选:B
11.C
解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选C.
12.A
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=CD=BC,
∵E是CD的中点,
∴CE:CD=1:2,
即CE:AB=1:2,
A、∵BP=PC,
∴BP=PC=BC,
没办法判定△ABP与△ECP中各边成比例,故A错误;
B、∵∠APE=90°,
∴∠APB+∠CPE=90°,
∵∠BAP+∠APB=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE,故B正确;
C、∵∠APB=∠EPC,
∴△ABP∽△EPC,故C正确;
D、∵BP=2PC,
∴PC:BP=1:2,
∴PC:BP=CE:AB=1:2,
∴△ABP∽△PCE,故D正确.
故选:A.
13.4
解:∵,
∴.
∵,,
∴,
解得:.
故答案为:4.
14.∠ACD=∠B或∠ADC=∠ACB或.
解:∵∠CAD =∠BAC,
根据两对角对应相等的两个三角形相似,可添加∠ACD=∠B或∠ADC=∠ACB,
∵∠CAD =∠BAC,∠ACD =∠B;
∴△ACD∽△ABC.
∵∠CAD =∠BAC,∠ADC =∠ACB;
∴△ACD∽△ABC.
根据两边对应成比例,夹角相等的两个三角形相似,可添加,
∵,∠CAD =∠BAC,
∴△ACD∽△ABC.
∴当∠ACD=∠B或∠ADC=∠ACB或时,△ACD∽△ABC.
故答案为:∠ACD=∠B或∠ADC=∠ACB或.
15.##1:2
解:过D作BF的平行线,交AC边于G,如下图所示:
∵D为BC中点,DG∥BF,
∴∠CGD=∠CFB,
又∵∠C=∠C,
∴△CDG∽△CBF,
∴,即:CG=CF=FG,
又E为AD的中点,BE的延长线交AC于F,DG∥BF,
同理可得:△AEF∽△ADG,
∴,即:AF=AG=FG,
∴AF=FG=GC,
∴.
故答案为:.
16.4
解:∵是直角三角形,
∴只要创造出一个直角时,才能满足题目中的条件,有以下几种情况:
当时,可得相似三角形;
当时,可得相似三角形;
当时,可得相似三角形;
当时,可得相似三角形;
∴满足条件的直线m有4条;
故答案是4.
17.添加条件:AB//CD,证明见解析(答案不唯一)
解:添加条件:.
证明:∵,,
∴,
∵,
∴,
∴.
18.见解析
解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
19.见解析
解:∵△ABC中,∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴.
20.(1)见解析 (2)见解析
(1)
解:∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵四边形ABCE为⊙O的内接四边形,
∴∠B+∠AEC=180°.
∵∠AED+∠AEC=180°.
∴∠B=∠AED.
∵AB=AC,
∴AB=∠ACB
∴∠ACB=∠AED.
∴△ABC∽△ADE.
(2)
解:如图,连接AO并延长,交BC于点M,连接OB、OC.
∵AB=AC,OB=OC,
∴AM垂直平分BC.
∴∠AMC=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAO=90°.
∵点A在⊙O上,
∴AD是⊙O的切线.
21.(1)①,③ (2)证明见解析
(1)
解:①剪下的角与原三角形有两个对应角相等,故两三角形相似,所以①正确;
②由题,,,,虽然,但无法确定夹角相等, 也无法确定DE与BC的比值,故 ,不相似,所以②错误.
③由题,,,,
∴,;
即,
∵是公共角.
∴
故③正确
④在,角形中有,但是无法确定,无法确定所以④错误.
故选:①,③
(2)
解:①∵,
∴
根据相似三角形的判定:两角分别对应相等的三角形是相似三角形
∴.
解:③∵,,,,
∴,;
即,
∵是公共角.
∴
根据相似三角形的判定:两别对应成比例,夹角相等的两个三角形相似.
答案第1页,共2页
一、单选题
1.如图,在三角形纸片ABC中,,,,沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.如图,甲、乙中各有两个三角形,其边长和角的度数如图上标注,则对甲、乙中两个三角形,下列说法正确的是( )
A.都相似 B.都不相似
C.只有甲中两个三角形相似 D.只有乙中两个三角形相似
3.如图,下列不能判定与相似的是( )
A. B. C. D.
4.下列说法,其中正确的有( )
①各有一个角是60°的两个等腰三角形相似;
②各有一个角是80°的两个等腰三角形相似;
③各有一个角是100°的两个等腰三角形相似;
④两边成比例的两个等腰三角形相似.
A.1个 B.2个 C.3个 D.4个
5.如图,是平行四边形ABCD的对角线BD上一点,AM的延长线交BC于点,交DC的延长线于点,图中相似三角形有( )
A.6对 B.5对 C.4对 D.3对
6.如图,,,AE、FD分别交BC于点G、H,则图中的相似三角形共有( )
A.3对 B.4对 C.5对 D.6对
7.如图,在△ABC中,∠A=60°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,有如下几种剪法,其中满足剪下的阴影三角形与△ABC相似的个数有( )
A.1个 B.2个 C.3个 D.4个
8.如图,和中,,则添加下列条件后无法判定的是( )
A. B. C. D.
9.如图, 已知在 中, 点 在边 上, 那么下列条件中 不能判定 的是( )
A. B.
C. D.
10.如图,P是直角△ABC斜边AB上任意一点(A,B两点除外),过点P作一条直线,使截得的三角形与△ABC相似,这样的直线可以作( )
A.4条 B.3条 C.2条 D.1条
11.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )
A. B. C. D.
12.如图,四边形是正方形,是边的中点,是边上的一动点,下列条件中,,△ABP不与△ECP相似的是( )
A. B.
C. D.
二、填空题
13.如图,在中,,若,,则的长为______cm.
14.如图,△ABC中,点D在边AB上,要使△ABC∽△ACD,添加一个条件是_______.(一种即可)
15.如图,AD是的中线,是AD的中点,BE的延长线交AC于点,那么______.
16.如图,在RtABC中,∠C=90°,∠A=60°,点P是AC的中点,若过点P的任意直线m截得的三角形与原ABC相似,那么这样的直线m的条数是___________.
三、解答题
17.如图,在△ABC和△ACD 中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使,并加以证明.
18.如图,已知∠EAC=∠DAB,∠D=∠B,求证:△ABC∽△ADE.
19.如图,中,, 于, 平分交于,交于.求证:
20.如图,⊙O是△ABC的外接圆,且AB=AC,四边形ABCD是平行四边形,边CD与⊙O交于点E,连接AE.
(1)求证△ABC∽△ADE;
(2)求证:AD是⊙O的切线.
21.如图,在中,,,,将沿着图示中虚线剪开,使剪下的小三角形与相似,下面有四种不同的剪法.
(1)请选择其中一种正确的剪法______(填序号);
(2)写出所选剪法中两个三角形相似的证明过程.
试卷第1页,共3页
参考答案:
1.B
解:在三角形纸片ABC中,AB=9,AC=6,BC=12.
A.因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.因为 ,对应边,又∠A=∠A,故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
C.因为 ,对应边,即:,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、因为 ,对应边, ,故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:B.
2.C
解:∵甲中两个三角形的两个内角分别为75°、35°和70°、75°,
∴两个三角形的另一个内角的度数分别为70°和35°,
∴两个三角形的三个内角分别对应相等,
∴甲中两个三角形相似,
∵,
∴乙中两个三角形不相似,
∴只有甲中两个三角形相似,
故选:C.
3.A
解:虽然,但∠ABD≠∠C,
∴△ABD与△ACB不相似,
∴选项A符合;
∵,∠A=∠A,
∴△ABD∽△ACB,
∴选项B不符合;
∵∠ABD=∠C,∠A=∠A,
∴△ABD∽△ACB,
∴选项C不符合;
∵∠ADB=∠ABC,∠A=∠A,
∴△ABD∽△ACB,
∴选项D不符合.
故选:A.
4.B
解:各有一个角是60°的两个等腰三角形都为等边三角形,它们相似,所以①正确;
顶角为80度的等腰三角形与底角为80度的等腰三角形不相似,所以②错误;
各有一个角是100°的两个等腰三角形的底角都为40度,它们相似,所以③正确;
两边成比例的两个等腰三角形不相似,所以④错误.
故选B.
5.A
解:∵四边形ABCD是平行四边形,
∴ , , ,
∵,
∴ ,
∵,
∴
∴,
则图中相似三角形有6对,它们分别是:,,,
故选:A.
6.D
解:∵,,
∴△BFH∽△BAG,
△BAG∽△CEG,
△BFH∽△CEG,
△BFH∽△CDH,
△CEG∽△CDH,
△CDH∽△BAG.
∴相似三角形共有6对.
故选C.
7.C
解:如图1,过点作于点,
,
,
,
,
,
在和中,,但或者,但,
则与不相似;
如图2,,
,
在和中,,
;
如图3和图4,剪下的阴影三角形均与有一组公共角,还有一组大小均为的相等的角,
所以图3和图4中,剪下的阴影三角形均与相似;
综上,满足剪下的阴影三角形与相似的个数是3个,
故选:C.
8.D
解:∵,,
∴ ,
故选项A不符合题意;
∵,,
∴,
故选项B不符合题意;
∵,,
∴,
故选项C不符合题意;
∵,但不一定相等,
∴不一定相似,
则添加条件后无法判定;
故选项D符合题意.
故选D.
9.A
解:而不一定相等,不能判断,故A符合题意;
,
而
故B不符合题意;
,
故C不符合题意;
,
故D不符合题意;
故选A
10.B
解:如图,过点P可作PE∥BC或PE″∥AC,
∴△APE∽△ABC、△PBE″∽△ABC;
过点P还可作PE′⊥AB,可得:∠EPA=∠C=90°,∠A=∠A
∴△APE∽△ACB;
∴满足这样条件的直线的作法共有3种.
故选:B
11.C
解:当CD是AB的垂线时,△ACD∽△CBD.
∵CD⊥AB,
∴∠CDA=∠BDC=90°,
∵∠ACB=90°,
∴∠A+∠ACD=∠ACD+∠BCD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD.
根据作图痕迹可知,
A选项中,CD是∠ACB的角平分线,不符合题意;
B选项中,CD不与AB垂直,不符合题意;
C选项中,CD是AB的垂线,符合题意;
D选项中,CD不与AB垂直,不符合题意;
故选C.
12.A
解:∵四边形ABCD是正方形,
∴∠B=∠C=90°,AB=CD=BC,
∵E是CD的中点,
∴CE:CD=1:2,
即CE:AB=1:2,
A、∵BP=PC,
∴BP=PC=BC,
没办法判定△ABP与△ECP中各边成比例,故A错误;
B、∵∠APE=90°,
∴∠APB+∠CPE=90°,
∵∠BAP+∠APB=90°,
∴∠BAP=∠CPE,
∴△ABP∽△PCE,故B正确;
C、∵∠APB=∠EPC,
∴△ABP∽△EPC,故C正确;
D、∵BP=2PC,
∴PC:BP=1:2,
∴PC:BP=CE:AB=1:2,
∴△ABP∽△PCE,故D正确.
故选:A.
13.4
解:∵,
∴.
∵,,
∴,
解得:.
故答案为:4.
14.∠ACD=∠B或∠ADC=∠ACB或.
解:∵∠CAD =∠BAC,
根据两对角对应相等的两个三角形相似,可添加∠ACD=∠B或∠ADC=∠ACB,
∵∠CAD =∠BAC,∠ACD =∠B;
∴△ACD∽△ABC.
∵∠CAD =∠BAC,∠ADC =∠ACB;
∴△ACD∽△ABC.
根据两边对应成比例,夹角相等的两个三角形相似,可添加,
∵,∠CAD =∠BAC,
∴△ACD∽△ABC.
∴当∠ACD=∠B或∠ADC=∠ACB或时,△ACD∽△ABC.
故答案为:∠ACD=∠B或∠ADC=∠ACB或.
15.##1:2
解:过D作BF的平行线,交AC边于G,如下图所示:
∵D为BC中点,DG∥BF,
∴∠CGD=∠CFB,
又∵∠C=∠C,
∴△CDG∽△CBF,
∴,即:CG=CF=FG,
又E为AD的中点,BE的延长线交AC于F,DG∥BF,
同理可得:△AEF∽△ADG,
∴,即:AF=AG=FG,
∴AF=FG=GC,
∴.
故答案为:.
16.4
解:∵是直角三角形,
∴只要创造出一个直角时,才能满足题目中的条件,有以下几种情况:
当时,可得相似三角形;
当时,可得相似三角形;
当时,可得相似三角形;
当时,可得相似三角形;
∴满足条件的直线m有4条;
故答案是4.
17.添加条件:AB//CD,证明见解析(答案不唯一)
解:添加条件:.
证明:∵,,
∴,
∵,
∴,
∴.
18.见解析
解:∵∠EAC=∠DAB,
∴∠EAC+∠DAC=∠DAB+∠DAC,即∠BAC=∠DAE,
又∵∠B=∠D,
∴△ABC∽△ADE.
19.见解析
解:∵△ABC中,∠BAC=90°,
∴∠BAD+∠CAD=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠C+∠CAD=90°,
∴∠C=∠BAD,
∵FB平分∠ABC,
∴∠ABF=∠EBD,
∴.
20.(1)见解析 (2)见解析
(1)
解:∵四边形ABCD是平行四边形,
∴∠B=∠D.
∵四边形ABCE为⊙O的内接四边形,
∴∠B+∠AEC=180°.
∵∠AED+∠AEC=180°.
∴∠B=∠AED.
∵AB=AC,
∴AB=∠ACB
∴∠ACB=∠AED.
∴△ABC∽△ADE.
(2)
解:如图,连接AO并延长,交BC于点M,连接OB、OC.
∵AB=AC,OB=OC,
∴AM垂直平分BC.
∴∠AMC=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠DAO=90°.
∵点A在⊙O上,
∴AD是⊙O的切线.
21.(1)①,③ (2)证明见解析
(1)
解:①剪下的角与原三角形有两个对应角相等,故两三角形相似,所以①正确;
②由题,,,,虽然,但无法确定夹角相等, 也无法确定DE与BC的比值,故 ,不相似,所以②错误.
③由题,,,,
∴,;
即,
∵是公共角.
∴
故③正确
④在,角形中有,但是无法确定,无法确定所以④错误.
故选:①,③
(2)
解:①∵,
∴
根据相似三角形的判定:两角分别对应相等的三角形是相似三角形
∴.
解:③∵,,,,
∴,;
即,
∵是公共角.
∴
根据相似三角形的判定:两别对应成比例,夹角相等的两个三角形相似.
答案第1页,共2页
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
