2021-2022学年人教版(五四制)九年级数学下册34.2解直角三角形及其应用课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(五四制)九年级数学下册34.2解直角三角形及其应用课后提升(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 882.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览




文档简介
解直角三角形及其应用
一、单选题
1.某斜坡的坡度,则该斜坡的坡角为( )
A.75° B.60° C.45° D.30°
2.如图,⊙A经过平面直角坐标系的原点O,交轴于点B(-4,0),交轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是( )
A. B. C. D.
3.如图,从一热气球的探测器A点,看一栋高楼顶部的仰角为55°,看这栋高楼底部的俯角为35°,若热气球与高楼的水平距离为35m,则这栋高楼度大约是( )(考数据:sin55°≈,cos55°≈,tan55°≈)
A.74米 B.80米 C.84米 D.98米
4.如图,是电杆的一根拉线,测得米,,则拉线的长为( )
A.米 B.米 C.米 D.米
5.如图,在离铁塔BC底部30米的D处,用测角仪从点A处测得塔顶B的仰角为α=30°,测角仪高AD为1.5米,则铁塔的高BC为( )
A.16.5米 B.(10+1.5)米
C.(15+1.5)米 D.(15+1.5)米
6.如图,将两个含30°角的直角三角板拼接在一起,点E为AD的中点,连接BE交AC于点F,则的值是( ).
A. B. C. D.
7.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
A.5 B. C.10﹣ D.15﹣
8.如图,是一水库大坝横断面的一部分,坝高,迎水斜坡,斜坡的坡角为,则的值为( )
A. B. C. D.
9.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑2m到A′时,梯脚B滑到B′,A′B′与地面的夹角为β,若tanα=,BB′=2m,则cosβ=( )
A. B. C. D.
10.如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.5米处,若国旗随国歌声冉冉升起,并在国歌播放46秒结束时到达旗杆顶端,则国旗匀速上升的速度为( )米/秒.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.0.3 B.0.2 C.0.25 D.0.35
11.如图,一艘测量船在A处测得灯塔S在它的南偏东60°方向,测量船继续向正东航行30海里后到达B处,这时测得灯塔S在它的南偏西75°方向,则灯塔S离观测点A的距离是( )
A.15海里 B.(15﹣15)海里
C.(15﹣15)海里 D.15海里
12.鹅岭公园是重庆最早的私家园林,前身为礼园,是国家级AAA旅游景区,园内有一瞰胜楼,登上高楼能欣赏到重庆的优美景色.周末,李明同学游览鹅岭公园,如图,在点A观察到瞰胜楼楼底点C的仰角为12°,楼顶点D的仰角为13°,测得斜坡BC的坡面距离BC510米,斜坡BC的坡度.则瞰胜楼的高度CD是( )米.(参考数据:tan12°≈0.2,tan13°≈0.23)
A.30 B.32 C.34 D.36
二、填空题
13.如图、、在上,连接、、,若,劣弧的度数是,.则图中阴影部分的面积是 __.
14.定义:等腰三角形中底边与腰的比叫做顶角正对(sad),即在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.如图,若在△ABC中,AB=AC,sinB=,则sadA的值是______.
15.如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10,,反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为________.
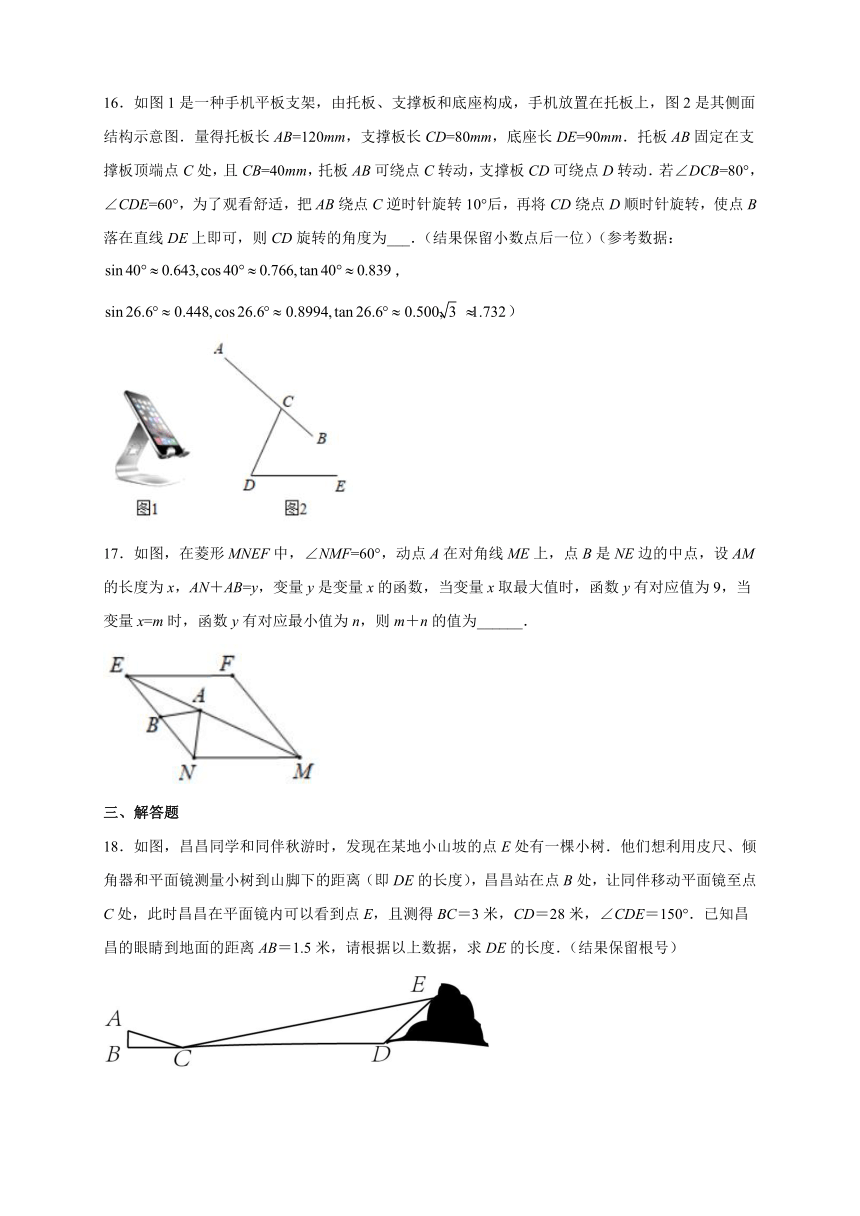
16.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长AB=120mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.若∠DCB=80°,∠CDE=60°,为了观看舒适,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,则CD旋转的角度为___.(结果保留小数点后一位)(参考数据:,)
17.如图,在菱形MNEF中,∠NMF=60°,动点A在对角线ME上,点B是NE边的中点,设AM的长度为x,AN+AB=y,变量y是变量x的函数,当变量x取最大值时,函数y有对应值为9,当变量x=m时,函数y有对应最小值为n,则m+n的值为______.
三、解答题
18.如图,昌昌同学和同伴秋游时,发现在某地小山坡的点E处有一棵小树.他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离(即DE的长度),昌昌站在点B处,让同伴移动平面镜至点C处,此时昌昌在平面镜内可以看到点E,且测得BC=3米,CD=28米,∠CDE=150°.已知昌昌的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
19.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,AB为体温监测有效识别区域的长度,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,站在点A处测得摄像头M的仰角为60°,求体温监测有效识别区域AB的长度.()结果精确到0.1米
20.郑州人民公园有一座摩天轮,天天很喜欢坐,某日天天突然想测量这座摩天轮的高度,于是他先走到摩天轮AB对面小山上的E点处,在E点测得摩天轮最高点A的仰角为34°,沿着坡度的山坡向下走了26米到达C处,再往前走了77米到达了B处,请帮天天算出摩天轮AB的高度.(参考数据:,,,结果精确到米)
21.钓鱼岛是我国固有领土,2021年4月26日,中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》,报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据.如图所示,点A是岛上最西端“西钓角”,点B是岛上最东端“东钓角”, AB长约3641米,点D是岛上的小黄鱼岛,且A、B、D三点共线.某日中国海监一艘执法船巡航到点C处时,恰好看到正北方的小黄鱼岛D,并测得∠ACD=70°,∠BCD=45°.根据以上数据,请求出此时执法船距离小黄鱼岛D的距离CD的值.(参考数据:tan70°≈2.75,sin70°≈0.94,cos70°≈0.34,结果精确到1米.)
22.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
试卷第1页,共3页
参考答案:
1.D
解:设该斜坡的坡角为α,
∵斜坡的坡度,
∴,
则=30°,
故选:D.
2.A
解:如图,连接BC,
∵∠BOC=90°,
∴BC是的直径,
∴点B,A,C三点共线.
∵B(-4,0),C(0,3),
∴OB=4,OC=3,
∴,
∴.
∵∠CDO=∠OBC,
∴.
故选:A.
3.A
解:过点A作AD⊥BC于D,
在Rt△ABD中,∠BAD=55°,AD=35m,tan∠BAD=,
∴BD=AD tan∠BAD≈35×=49(m),
在Rt△ACD中,∠ACD=90°﹣∠CAD=55°,AD=35m,tan∠ACD=,
∴CD=≈=25(m),
∴BC=BD+CD=49+25=74(m),
故选:A.
4.D
解:,
,
米,
米;
故选D.
5.B
解:如图所示,过点A作AE⊥BC,E为垂足,
则四边形ADCE为矩形,AE=30米,CE=AD=1.5米,
在中,,
∴(米),
∴米,
故选B.
6.D
解:在Rt△ABC中,∠BAC=30°,
设BC=x,则AB=x,AC=2x,
在Rt△ADC中,∠DAC=30°,
则CD=tan30°×AC=,
AD=2CD=,
∵E为AD的中点,连接CE,
∴CE=AE=,
∠EAC=∠ECA,
∴∠ECA=∠BAC,
又∵∠AFB=∠CFE,
∴△AFB∽△CFE,
∴,
故选:D.
7.D
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=10×tan60°=,
∵AB∥CF,
∴BM=BC×sin30°=×=,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=,
∴CD=CM﹣MD=15﹣.
故选:D.
8.B
解:过点A作AC⊥BD,垂足为C,
∵坝高h=60m,迎水斜坡AB=100m,
∴BC= =80(m),
则tanα= .
故选:B.
9.A
解:如图:
在Rt△ABC中,∠ACB=90°,tanα=,
∴可设AC=4x m,那么BC=3x m,
∴AB==5x m,
∴A′B′=AB=5x(m).
在Rt△A′B′C中,∠A′CB′=90°,A′C=(4x-2)m,B′C=(3x+2)m,
∴(4x-2)2+(3x+2)2=(5x)2,
解得:x=2,
∴A′C=6m,B′C=8m,A′B′=10m,
∴cosβ=.
故选:A.
10.C
解:在Rt△BCD中,BD=8米,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=8米,
在Rt△ACD中,CD=8米,∠ACD=37°,
∴AD=CD tan37°≈8×0.75=6(米),
∴旗杆AB的高为:AD+BD=6+8=14(米);
升旗时,国旗上升高度是:14﹣2.5=11.5(米),
∵耗时46s,
∴国旗匀速上升的速度为:=0.25(米/秒),
故选:C.
11.B
解:过S作SC⊥AB于C,在AB上截取CD=AC,
∴AS=DS,
∴∠CDS=∠CAS=30°,
∵∠ABS=15°,
∴∠DSB=15°,
∴SD=BD,
设CS=x海里,
在Rt△ASC中,∠CAS=30°,
∴AC=x(海里),AS=DS=BD=2x(海里),
∵AB=30海里,
∴x+x+2x=30,
解得:x=,
∴AS=(15﹣15)海里.
故选:B.
12.D
解:由斜坡BC的坡度,设、,
在中,
,
由求得,
∴米、米,
在中,
(米),
在中,
(米),
则(米).
故选:D.
13.##
解:,劣弧的度数是,
,,,
,
,
,
,
解得:,
阴影部分的面积
,
故答案为:.
14.
解:过点作,垂足为.
,,
.
,
设,,
则.
.
.
故答案为:.
15.####
解:∵斜边AO=10,sin∠AOB,
∴sin∠AOB,
∴AB=6,
∴OB8,
∴A点坐标为(﹣8,﹣6),
而C点为OA的中点,
∴C点坐标为(﹣4,﹣3),
又∵反比例函数y的图象经过点C,
∴k=(﹣4)×(﹣3)=12,即反比例函数的解析式为y,
∵D点在反比例函数的图象上,且它的横坐标为﹣8,
∴当x=﹣8,y,
∴D点坐标为(8,),
∴BD的长为.
故答案为:
16.33.4°
解:如图所示:
由题意可知:
∠DCB=80°+10°=90°,
在Rt△DCB中,DC=80mm,CB=40mm,
∴tan∠CDB= ,
∴∠CDB≈26.6°,
∴CD旋转的角度约为:60°-26.6°=33.4°,
故答案为:33.4°.
17.
解:如图,连接AF,FN,
∵点B是NE边的中点,
∴BN=EB=EN,
∵动点A在对角线ME上,
∴当点A与点E重合时,AM有最大值,
∴y=EN+EB=9,
∴EB=3,EN=6,
∵四边形ABCD是菱形,∠NMF=60°,
∴EF=EN=6,∠FEN=60°,∠NEM=30°,点F与点N关于EM对称,
∴△EFN是等边三角形,
∵y=AN+AB=AF+AB=BF,
∴当点A,点F,点B共线时,y有最小值,
此时,,,
∴,
∴,
故答案为:.
18.的长为米
解:过E作于F,
∵,
∴,
设为米,则米,米,
∵,,
∴,
∴即,
解得,
∴(米) .
∴的长度为米.
19.6.9米.
解:过D作DF⊥ME于F,
∵AC与BD都是小明身高,
∴AC∥BD,且AC=BD,∠DBA=90°
∴四边形DBAC为矩形,
∴AB=CD,CD∥AB,
∴DF∥BE,BD∥FE,∠DBE=90°,
∴四边形DBEF为矩形,
∴FE=BD=1.5米,
∴MF=ME-EF=7.5-1.5=6米,
在Rt△MFC中tan60°=,
∴米,
在Rt△MFD中,tan30°=
∴米,
∴CD=DF-CF=≈4×1.73=6.92≈6.9米,
∴AB=6.9米.
20.摩天轮的高度约为78米.
解:过点E作的延长线于点F,作于点H,
在中,
,
,
, (米),
,
解得(米),
(米),
(米),(米).
在中,
,
(米),
(米).
答:摩天轮的高度约为78米.
21.执法船距离小黄鱼岛D的距离CD约为971米.
解:设CD=x米,
Rt△ACD中,tan∠ACD=,
∴AD=2.75x米,
Rt△BCD中,∠BCD=45°,
∴BD=CD=x米,
∴2.75x+x=3641,
解得x≈971,
答:执法船距离小黄鱼岛D的距离CD约为971米.
22.(1)篮板底部支架HE与支架AF所成的角∠FHE的度数为45°
(2)篮板底部点E到地面的距离是(+)米
解:(1)
在Rt△EFH中,cos∠FHE= ,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)
延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB= ,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°= ,
∴EM=EG+GM= ,
答:篮板底部点E到地面的距离是()米.
答案第1页,共2页
一、单选题
1.某斜坡的坡度,则该斜坡的坡角为( )
A.75° B.60° C.45° D.30°
2.如图,⊙A经过平面直角坐标系的原点O,交轴于点B(-4,0),交轴于点C(0,3),点D为第二象限内圆上一点.则∠CDO的正弦值是( )
A. B. C. D.
3.如图,从一热气球的探测器A点,看一栋高楼顶部的仰角为55°,看这栋高楼底部的俯角为35°,若热气球与高楼的水平距离为35m,则这栋高楼度大约是( )(考数据:sin55°≈,cos55°≈,tan55°≈)
A.74米 B.80米 C.84米 D.98米
4.如图,是电杆的一根拉线,测得米,,则拉线的长为( )
A.米 B.米 C.米 D.米
5.如图,在离铁塔BC底部30米的D处,用测角仪从点A处测得塔顶B的仰角为α=30°,测角仪高AD为1.5米,则铁塔的高BC为( )
A.16.5米 B.(10+1.5)米
C.(15+1.5)米 D.(15+1.5)米
6.如图,将两个含30°角的直角三角板拼接在一起,点E为AD的中点,连接BE交AC于点F,则的值是( ).
A. B. C. D.
7.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是( )
A.5 B. C.10﹣ D.15﹣
8.如图,是一水库大坝横断面的一部分,坝高,迎水斜坡,斜坡的坡角为,则的值为( )
A. B. C. D.
9.如图,AB是斜靠在墙上的长梯,AB与地面夹角为α,当梯顶A下滑2m到A′时,梯脚B滑到B′,A′B′与地面的夹角为β,若tanα=,BB′=2m,则cosβ=( )
A. B. C. D.
10.如图,小东在教学楼距地面8米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.5米处,若国旗随国歌声冉冉升起,并在国歌播放46秒结束时到达旗杆顶端,则国旗匀速上升的速度为( )米/秒.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A.0.3 B.0.2 C.0.25 D.0.35
11.如图,一艘测量船在A处测得灯塔S在它的南偏东60°方向,测量船继续向正东航行30海里后到达B处,这时测得灯塔S在它的南偏西75°方向,则灯塔S离观测点A的距离是( )
A.15海里 B.(15﹣15)海里
C.(15﹣15)海里 D.15海里
12.鹅岭公园是重庆最早的私家园林,前身为礼园,是国家级AAA旅游景区,园内有一瞰胜楼,登上高楼能欣赏到重庆的优美景色.周末,李明同学游览鹅岭公园,如图,在点A观察到瞰胜楼楼底点C的仰角为12°,楼顶点D的仰角为13°,测得斜坡BC的坡面距离BC510米,斜坡BC的坡度.则瞰胜楼的高度CD是( )米.(参考数据:tan12°≈0.2,tan13°≈0.23)
A.30 B.32 C.34 D.36
二、填空题
13.如图、、在上,连接、、,若,劣弧的度数是,.则图中阴影部分的面积是 __.
14.定义:等腰三角形中底边与腰的比叫做顶角正对(sad),即在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=.如图,若在△ABC中,AB=AC,sinB=,则sadA的值是______.
15.如图,将Rt△ABO放置在直角坐标系中,OB边与x轴重合,AO=10,,反比例函数(x<0)的图象经过AO的中点C,且与AB交于点D,则BD的长为________.
16.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图.量得托板长AB=120mm,支撑板长CD=80mm,底座长DE=90mm.托板AB固定在支撑板顶端点C处,且CB=40mm,托板AB可绕点C转动,支撑板CD可绕点D转动.若∠DCB=80°,∠CDE=60°,为了观看舒适,把AB绕点C逆时针旋转10°后,再将CD绕点D顺时针旋转,使点B落在直线DE上即可,则CD旋转的角度为___.(结果保留小数点后一位)(参考数据:,)
17.如图,在菱形MNEF中,∠NMF=60°,动点A在对角线ME上,点B是NE边的中点,设AM的长度为x,AN+AB=y,变量y是变量x的函数,当变量x取最大值时,函数y有对应值为9,当变量x=m时,函数y有对应最小值为n,则m+n的值为______.
三、解答题
18.如图,昌昌同学和同伴秋游时,发现在某地小山坡的点E处有一棵小树.他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离(即DE的长度),昌昌站在点B处,让同伴移动平面镜至点C处,此时昌昌在平面镜内可以看到点E,且测得BC=3米,CD=28米,∠CDE=150°.已知昌昌的眼睛到地面的距离AB=1.5米,请根据以上数据,求DE的长度.(结果保留根号)
19.在疫情防控工作中,某学校在校门口的大门上方安装了一个人体测温摄像头.如图,学校大门高ME=7.5米,AB为体温监测有效识别区域的长度,小明身高BD=1.5米,他站在点B处测得摄像头M的仰角为30°,站在点A处测得摄像头M的仰角为60°,求体温监测有效识别区域AB的长度.()结果精确到0.1米
20.郑州人民公园有一座摩天轮,天天很喜欢坐,某日天天突然想测量这座摩天轮的高度,于是他先走到摩天轮AB对面小山上的E点处,在E点测得摩天轮最高点A的仰角为34°,沿着坡度的山坡向下走了26米到达C处,再往前走了77米到达了B处,请帮天天算出摩天轮AB的高度.(参考数据:,,,结果精确到米)
21.钓鱼岛是我国固有领土,2021年4月26日,中华人民共和国自然资源部在其官网上公布《钓鱼岛及其附属岛屿地形地貌调查报告》,报告公布了钓鱼岛及其附属岛屿的高分辨率海岛地形数据.如图所示,点A是岛上最西端“西钓角”,点B是岛上最东端“东钓角”, AB长约3641米,点D是岛上的小黄鱼岛,且A、B、D三点共线.某日中国海监一艘执法船巡航到点C处时,恰好看到正北方的小黄鱼岛D,并测得∠ACD=70°,∠BCD=45°.根据以上数据,请求出此时执法船距离小黄鱼岛D的距离CD的值.(参考数据:tan70°≈2.75,sin70°≈0.94,cos70°≈0.34,结果精确到1米.)
22.如图1,2分别是某款篮球架的实物图与示意图,已知AB⊥BC于点B,底座BC的长为1米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC,EF⊥EH于点E,已知AH长米,HF长米,HE长1米.
(1)求篮板底部支架HE与支架AF所成的角∠FHE的度数.
(2)求篮板底部点E到地面的距离.(结果保留根号)
试卷第1页,共3页
参考答案:
1.D
解:设该斜坡的坡角为α,
∵斜坡的坡度,
∴,
则=30°,
故选:D.
2.A
解:如图,连接BC,
∵∠BOC=90°,
∴BC是的直径,
∴点B,A,C三点共线.
∵B(-4,0),C(0,3),
∴OB=4,OC=3,
∴,
∴.
∵∠CDO=∠OBC,
∴.
故选:A.
3.A
解:过点A作AD⊥BC于D,
在Rt△ABD中,∠BAD=55°,AD=35m,tan∠BAD=,
∴BD=AD tan∠BAD≈35×=49(m),
在Rt△ACD中,∠ACD=90°﹣∠CAD=55°,AD=35m,tan∠ACD=,
∴CD=≈=25(m),
∴BC=BD+CD=49+25=74(m),
故选:A.
4.D
解:,
,
米,
米;
故选D.
5.B
解:如图所示,过点A作AE⊥BC,E为垂足,
则四边形ADCE为矩形,AE=30米,CE=AD=1.5米,
在中,,
∴(米),
∴米,
故选B.
6.D
解:在Rt△ABC中,∠BAC=30°,
设BC=x,则AB=x,AC=2x,
在Rt△ADC中,∠DAC=30°,
则CD=tan30°×AC=,
AD=2CD=,
∵E为AD的中点,连接CE,
∴CE=AE=,
∠EAC=∠ECA,
∴∠ECA=∠BAC,
又∵∠AFB=∠CFE,
∴△AFB∽△CFE,
∴,
故选:D.
7.D
解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=10×tan60°=,
∵AB∥CF,
∴BM=BC×sin30°=×=,
CM=BC×cos30°=15,
在△EFD中,∠F=90°,∠E=45°,
∴∠EDF=45°,
∴MD=BM=,
∴CD=CM﹣MD=15﹣.
故选:D.
8.B
解:过点A作AC⊥BD,垂足为C,
∵坝高h=60m,迎水斜坡AB=100m,
∴BC= =80(m),
则tanα= .
故选:B.
9.A
解:如图:
在Rt△ABC中,∠ACB=90°,tanα=,
∴可设AC=4x m,那么BC=3x m,
∴AB==5x m,
∴A′B′=AB=5x(m).
在Rt△A′B′C中,∠A′CB′=90°,A′C=(4x-2)m,B′C=(3x+2)m,
∴(4x-2)2+(3x+2)2=(5x)2,
解得:x=2,
∴A′C=6m,B′C=8m,A′B′=10m,
∴cosβ=.
故选:A.
10.C
解:在Rt△BCD中,BD=8米,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=8米,
在Rt△ACD中,CD=8米,∠ACD=37°,
∴AD=CD tan37°≈8×0.75=6(米),
∴旗杆AB的高为:AD+BD=6+8=14(米);
升旗时,国旗上升高度是:14﹣2.5=11.5(米),
∵耗时46s,
∴国旗匀速上升的速度为:=0.25(米/秒),
故选:C.
11.B
解:过S作SC⊥AB于C,在AB上截取CD=AC,
∴AS=DS,
∴∠CDS=∠CAS=30°,
∵∠ABS=15°,
∴∠DSB=15°,
∴SD=BD,
设CS=x海里,
在Rt△ASC中,∠CAS=30°,
∴AC=x(海里),AS=DS=BD=2x(海里),
∵AB=30海里,
∴x+x+2x=30,
解得:x=,
∴AS=(15﹣15)海里.
故选:B.
12.D
解:由斜坡BC的坡度,设、,
在中,
,
由求得,
∴米、米,
在中,
(米),
在中,
(米),
则(米).
故选:D.
13.##
解:,劣弧的度数是,
,,,
,
,
,
,
解得:,
阴影部分的面积
,
故答案为:.
14.
解:过点作,垂足为.
,,
.
,
设,,
则.
.
.
故答案为:.
15.####
解:∵斜边AO=10,sin∠AOB,
∴sin∠AOB,
∴AB=6,
∴OB8,
∴A点坐标为(﹣8,﹣6),
而C点为OA的中点,
∴C点坐标为(﹣4,﹣3),
又∵反比例函数y的图象经过点C,
∴k=(﹣4)×(﹣3)=12,即反比例函数的解析式为y,
∵D点在反比例函数的图象上,且它的横坐标为﹣8,
∴当x=﹣8,y,
∴D点坐标为(8,),
∴BD的长为.
故答案为:
16.33.4°
解:如图所示:
由题意可知:
∠DCB=80°+10°=90°,
在Rt△DCB中,DC=80mm,CB=40mm,
∴tan∠CDB= ,
∴∠CDB≈26.6°,
∴CD旋转的角度约为:60°-26.6°=33.4°,
故答案为:33.4°.
17.
解:如图,连接AF,FN,
∵点B是NE边的中点,
∴BN=EB=EN,
∵动点A在对角线ME上,
∴当点A与点E重合时,AM有最大值,
∴y=EN+EB=9,
∴EB=3,EN=6,
∵四边形ABCD是菱形,∠NMF=60°,
∴EF=EN=6,∠FEN=60°,∠NEM=30°,点F与点N关于EM对称,
∴△EFN是等边三角形,
∵y=AN+AB=AF+AB=BF,
∴当点A,点F,点B共线时,y有最小值,
此时,,,
∴,
∴,
故答案为:.
18.的长为米
解:过E作于F,
∵,
∴,
设为米,则米,米,
∵,,
∴,
∴即,
解得,
∴(米) .
∴的长度为米.
19.6.9米.
解:过D作DF⊥ME于F,
∵AC与BD都是小明身高,
∴AC∥BD,且AC=BD,∠DBA=90°
∴四边形DBAC为矩形,
∴AB=CD,CD∥AB,
∴DF∥BE,BD∥FE,∠DBE=90°,
∴四边形DBEF为矩形,
∴FE=BD=1.5米,
∴MF=ME-EF=7.5-1.5=6米,
在Rt△MFC中tan60°=,
∴米,
在Rt△MFD中,tan30°=
∴米,
∴CD=DF-CF=≈4×1.73=6.92≈6.9米,
∴AB=6.9米.
20.摩天轮的高度约为78米.
解:过点E作的延长线于点F,作于点H,
在中,
,
,
, (米),
,
解得(米),
(米),
(米),(米).
在中,
,
(米),
(米).
答:摩天轮的高度约为78米.
21.执法船距离小黄鱼岛D的距离CD约为971米.
解:设CD=x米,
Rt△ACD中,tan∠ACD=,
∴AD=2.75x米,
Rt△BCD中,∠BCD=45°,
∴BD=CD=x米,
∴2.75x+x=3641,
解得x≈971,
答:执法船距离小黄鱼岛D的距离CD约为971米.
22.(1)篮板底部支架HE与支架AF所成的角∠FHE的度数为45°
(2)篮板底部点E到地面的距离是(+)米
解:(1)
在Rt△EFH中,cos∠FHE= ,
∴∠FHE=45°,
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)
延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB= ,
∴AB=BCtan60°=1×=,
∴GM=AB=,
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°= ,
∴EM=EG+GM= ,
答:篮板底部点E到地面的距离是()米.
答案第1页,共2页
