2021-2022学年人教版(五四制)九年级数学下册34.1锐角三角函数课后提升(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版(五四制)九年级数学下册34.1锐角三角函数课后提升(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 616.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 00:00:00 | ||
图片预览




文档简介
锐角三角函数
一、单选题
1.如图,在中,,,,下列三角函数表示正确的是( )
A. B. C. D.
2.在直角中,已知,,求( )
A. B. C. D.
3.如图,中,,,则( )
A. B. C. D.
4.如图,△ABC是等边三角形,△BCD是等腰三角形,且BD=CD,过点D作AB的平行线交AC于点E,若AB=8,DE=6,则BD的长为( )
A.6 B. C. D.
5.在网格中的位置如图所示(每个小正方形边长为1),于D,下列四个选项中,错误的是( ).
A. B. C. D.
6.如图,在菱形ABCD中,O、E分别是AC、AD的中点,连接OE,若AB=10,AC=12,则tan∠AOE的值为( )
A. B. C. D.
7.如图,在⊙O中,弦的长是,弦的弦心距为6cm,是⊙O优弧上一点.则的度数为( )
A.60° B.45° C.30° D.80°
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
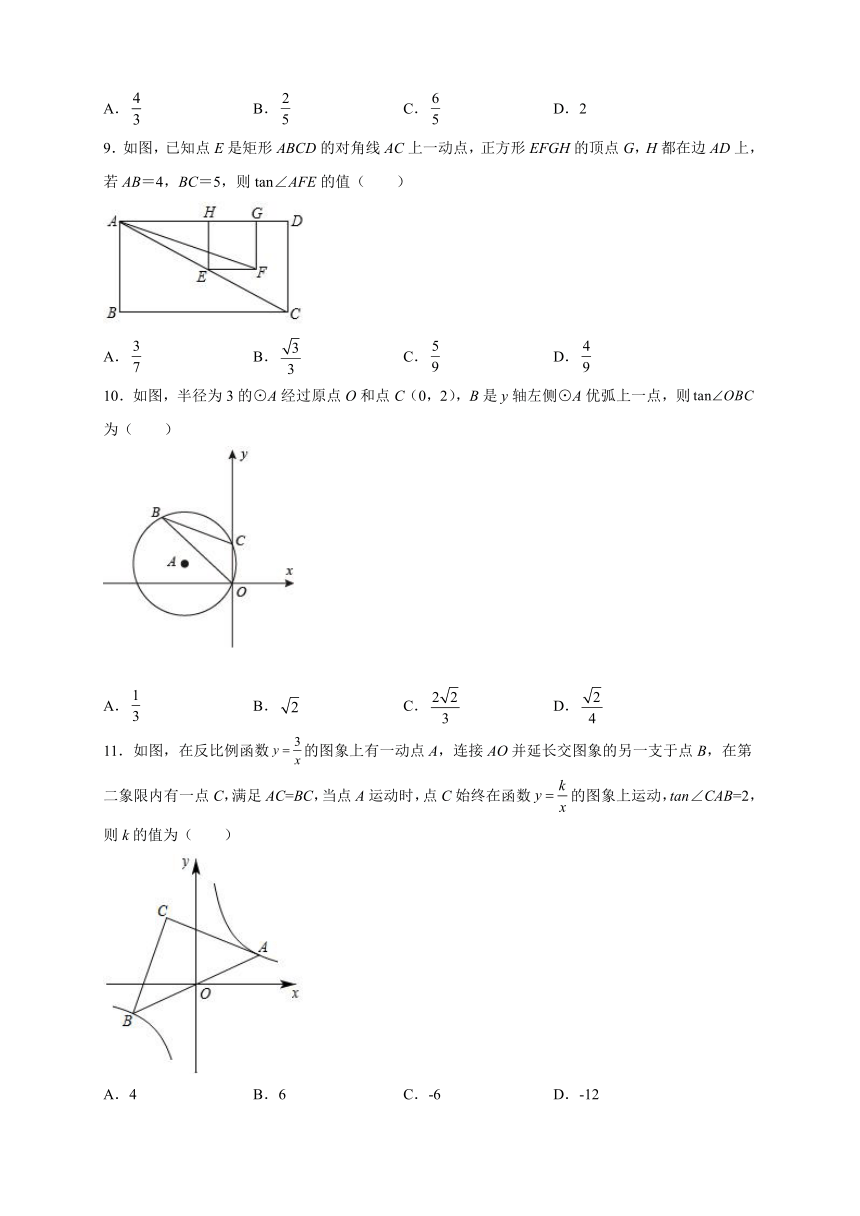
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
A. B. C. D.
10.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则为( )
A. B. C. D.
11.如图,在反比例函数的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数的图象上运动,tan∠CAB=2,则k的值为( )
A.4 B.6 C.-6 D.-12
12.如图,在△ABC中,∠ABC=90°,分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N,作直线MN交AC于点E,交BC于点F,若,则tan∠ACB的值为( )
A. B. C. D.
二、填空题
13.若,则锐角α为______度.
14.如图,4×4的正方形网格中,A、B、C、D为格点,连接AB、CD相交于点E,则tan∠AEC的值是 ___.
15.如图,平面直角坐标系中正方形ABCD,已知A(2,0),B(0,6),则sin∠COA=__.
16.如图,在菱形ABCD中,于点E,与BD交于点F,若,则和的面积比为______.
17.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=,则⊙O的直径长为_____.
三、解答题
18.计算:
(1);
(2).
19.如图,已知Rt△ABC中,∠BAC=90°,BC=6,AC=4,以A为圆心,AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的余弦值.
20.如图,点C在⊙O的直径AB的延长线上,点D是⊙O上一点,过C作EC⊥AC,交AD的延长线于E,连接DB,且CD=CE.
(1)求证:DC与⊙O相切.
(2)若AB=10,tan∠BDC=,求CE的长.
21.如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)若DC=6,tan∠P=,求BC的长.
22.如图1,四边形ABCD内接于,对角线 AC 是的直径,AB,DC 的延长线交于点E,.
(1)求证:是等腰三角形;
(2)如图2,若BD平分,求的值;
(3)如图1,若,,求y与x的函数关系式.
试卷第1页,共3页
参考答案:
1.B
解:,,
, 故选项A错误;
,故选项B正确;
, 故选项C错误;
, 故选项D错误;
故选:B.
2.C
解:如图,在RtABC中,
∵,
∴设a=k,c=3k,
由勾股定理得:
∴.
故选:C.
3.D
解:∵,
∴.
∴.
故选:D.
4.B
解:连接AD交BC于点O,取AC中点N,连接ON,如图,
∵△ABC是等边三角形,
∴AB=AC=BC=8,∠ABC=60°,
∵△BCD是等腰三角形,
∴BD=DC,
∴AD垂直平分BC,
∴BO=CO=4,
∵AN=CN,
∴ON=AB=4,,
∵,
∴,
∴,
∴,
∴OD=AO,
∴tan∠ABO=,即,
∴,
∴OD=,
在Rt△BOD中,
,
故选:B.
5.C
解:观察图象可知,△ADB是等腰直角三角形,BD=AD=2,CD=1,
∴AB==2,AC==,
∴sinα=cosα=,故选项A正确;
tanC==2,故选项B正确;
tanα=1,故选项D正确;
∵sinβ==,cosβ=,∴sinβ≠cosβ,故选项C错误.
故选:C.
6.D
解:如图,连接OD,
∵四边形ABCD为菱形,
∴AD=CD=AB=10.
∵O是AC的中点,
∴OD⊥AC,OA=OCAC=6,
由勾股定理得,OD,
∵O、E分别是AC、AD的中点,
∴OE是△ACD的中位线,
∴OE∥CD,
∴∠AOE=∠ACD,
∴tan∠AOE=tan∠ACD,
故选:D.
7.A
解:∵弦的长是,弦的弦心距OC为6cm,
∴OC⊥AB,AC=CB=AB=6(cm),OC=6cm,∠AOC=∠BOC,
,
∴∠AOC=∠BOC=60°,即∠AOB=120°,
∴∠AEB=∠AOB =60°,
故选:A.
8.C
解:延长AD、BC,两线交于O,
在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB-BC=4-2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,
由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴,
∴,
解得:DC=,
故选:C.
9.D
解:∵EH∥CD,
∴△AEH∽△ACD.
∴,
∵AB=CD=4,BC=AD=5,
∴=.
设EH=4x,则AH=5x,
∴HG=GF=4x.
∵EF∥AD,
∴∠AFE=∠FAG,
∴tan∠AFE=tan∠FAG==.
故选:D.
10.D
解:
解:如图所示,设与x轴的另一个交点为D,连接CD,
∵,
∴是的直径,在中,,,
∴,
∴,
由圆周角定理可知,,
∴,
故选:D.
11.D
解:连接OC,作CM⊥x轴于M,AN⊥x轴于N,如图,
∵A、B两点为反比例函数与正比例函数的两交点,
∴点A、点B关于原点对称,
∴OA=OB,
∵CA=CB,
∴OC⊥AB,
在Rt△AOC中,tan∠CAO==2,
∵∠COM+∠AON=90°,∠AON+∠OAN=90°,
∴∠COM=∠OAN,
∴Rt△OCM∽Rt△AON,
∴4,
而S△OAN=×|3|=,
∴S△CMO=6,
∵|k|=6,
而k<0,
∴k=-12.
故选:D.
12.D
解:连接AF.
由作图可知,MN垂直平分线段AC,
∴FA=FC,
∵BF:FC=3:5,
∴可以假设BF=3k,CF=AF=5k,
∵∠B=90°,
∴AB,
∴BC=BF+CF=8k,
∴tan∠ACB,
故选:D.
13.60
解:∵α为锐角,且cosα=0.5,
∴角α的度数为60°.
故答案为:60.
14.3
解:连接DB,连接格点D、F交AB于F,如图,
由网格图可知,DB=DC,DB⊥DC,∠AEC=∠BED,
∵DFAC,
∴,
∴,
∴tan∠AEC=tan∠BED=3.
故答案为:3.
15.##
解:如图,过点C作CE⊥y轴于E,
∵A(2,0),B(0,6),
∴OA=2,OB=6,
在正方形ABCD中,AB=BC,∠ABC=90°,
∵∠ABO+∠CBE=90°,∠BCE+∠CBE=90°,
∴∠ABO=∠BCE,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=2,CE=OB=6,
∴OE=OB+BE=6+2=8,
在Rt△OCE中,,
∵CE⊥y轴,x轴⊥y轴,
∴CE∥x轴,
∴∠OCE=∠COA,
∴sin∠COA=sin∠OCE.
故答案为:.
16.
解:于,
,
,
可以假设,,则,
四边形是菱形,
,,
,
,
.
故答案为:.
17.
解:延长AO交⊙O于点D,连接CD,
∵BA与⊙O相切,
∴DA⊥AB,
∴∠DAC+∠BAC=90°,
∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠DAC+∠D=90°,
∴∠D=∠BAC,
∵tan∠BAC=,
∴tanD=,即=,
∵AC=4,
∴CD=12,
由勾股定理得,AD===.
故答案为:.
18.(1) (2)
解:(1)
(2)
19.(1) (2)
解:(1)过点A作AH⊥BD于H,如图1所示:
∵Rt△ABC,∠BAC=90°,BC=6,AC=4,
∴AB===2,
∵AB AC=BC AH,
∴AH===,
∴BH===,
∵AH⊥BD,
∴BH=HD=,
∴BD=;
(2)过点D作DM⊥AC于M,如图2所示:
由(1)得:AH=,BD=,AB=2,
∴AD=AB=2,CD=BC﹣BD=6﹣=,
∵AH CD=DM AC,
∴DM===,
在Rt△ADM中,由勾股定理得:AM===,
∴cos∠DAC===.
20.(1)见解析 (2)
(1)
证明:连接OD,
∵CE⊥AC,
∴∠ACE=90°,
∴∠A+∠E=90°,
∵CD=CE,
∴∠E=∠CDE,
∴∠A+∠CDE=90°,
∵OA=OD,
∴∠A=∠ADO,
∴∠ADO+∠CDE=90°,
∴∠ODC=90°,
∴OD⊥DC,
∴DC与⊙O相切;
(2)
解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
又∵∠BDC+∠ODB=90°,
∴∠BDC=∠A,
∵∠BCD=∠ACD,
∴△BCD∽△DCA,
∴,
∵tan∠BDC=tan∠A=,
设CB=x,则CD=2x,
∴CD2=CB CA,
∴,
∴x=,
∴CD=CE=.
21.(1)见解析 (2)3
证明:(1)如图,连接OD,
∵PD是切线,
∴OD⊥PD,
∴∠ODP=90°,
∴∠ODB+∠PDB=90°.
∵CD⊥BC,
∴∠CDB+∠DBC=90°.
∵OB=OD,
∴∠ODB=∠OBD,
∴∠CDB=∠PDB,
∴DB平分∠PDC.
(2)作BE⊥PD,如图.
∵DB平分∠PDC,BC⊥CD,BE⊥PD,
∴BC=BE.
在Rt△PDC中,,
∴PC=8,
∴.
设BC=x,则BE=x,PB=8-x.
∵∠EPB=∠CPD,
∴,
∴,
即,
解得x=3.
所以BC的长为3.
22.(1)见解析 (2) (3)
解:(1)如图1,∵,
∴,
∵四边形ABCD内接于,
∴,
∵,
∴,;
(2)如图2,作于F,
设,
∵AC为直径,
∴,,,
由(1)得,
∵,∴,,
∵,
∴;
(3)如图1,过B作于F,
设,,由(1)知
∵,
∴,
,,
∵,
∴,
,,,
∵,
∴,
即,即,
∵,
∴
答案第1页,共2页
一、单选题
1.如图,在中,,,,下列三角函数表示正确的是( )
A. B. C. D.
2.在直角中,已知,,求( )
A. B. C. D.
3.如图,中,,,则( )
A. B. C. D.
4.如图,△ABC是等边三角形,△BCD是等腰三角形,且BD=CD,过点D作AB的平行线交AC于点E,若AB=8,DE=6,则BD的长为( )
A.6 B. C. D.
5.在网格中的位置如图所示(每个小正方形边长为1),于D,下列四个选项中,错误的是( ).
A. B. C. D.
6.如图,在菱形ABCD中,O、E分别是AC、AD的中点,连接OE,若AB=10,AC=12,则tan∠AOE的值为( )
A. B. C. D.
7.如图,在⊙O中,弦的长是,弦的弦心距为6cm,是⊙O优弧上一点.则的度数为( )
A.60° B.45° C.30° D.80°
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A. B. C. D.2
9.如图,已知点E是矩形ABCD的对角线AC上一动点,正方形EFGH的顶点G,H都在边AD上,若AB=4,BC=5,则tan∠AFE的值( )
A. B. C. D.
10.如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则为( )
A. B. C. D.
11.如图,在反比例函数的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数的图象上运动,tan∠CAB=2,则k的值为( )
A.4 B.6 C.-6 D.-12
12.如图,在△ABC中,∠ABC=90°,分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N,作直线MN交AC于点E,交BC于点F,若,则tan∠ACB的值为( )
A. B. C. D.
二、填空题
13.若,则锐角α为______度.
14.如图,4×4的正方形网格中,A、B、C、D为格点,连接AB、CD相交于点E,则tan∠AEC的值是 ___.
15.如图,平面直角坐标系中正方形ABCD,已知A(2,0),B(0,6),则sin∠COA=__.
16.如图,在菱形ABCD中,于点E,与BD交于点F,若,则和的面积比为______.
17.如图,OA、OC都是⊙O的半径,点B在OC的延长线上,BA与⊙O相切于点A,连接AC,若AC=4,tan∠BAC=,则⊙O的直径长为_____.
三、解答题
18.计算:
(1);
(2).
19.如图,已知Rt△ABC中,∠BAC=90°,BC=6,AC=4,以A为圆心,AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的余弦值.
20.如图,点C在⊙O的直径AB的延长线上,点D是⊙O上一点,过C作EC⊥AC,交AD的延长线于E,连接DB,且CD=CE.
(1)求证:DC与⊙O相切.
(2)若AB=10,tan∠BDC=,求CE的长.
21.如图,点D在⊙O上,过点D的切线交直径AB延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)若DC=6,tan∠P=,求BC的长.
22.如图1,四边形ABCD内接于,对角线 AC 是的直径,AB,DC 的延长线交于点E,.
(1)求证:是等腰三角形;
(2)如图2,若BD平分,求的值;
(3)如图1,若,,求y与x的函数关系式.
试卷第1页,共3页
参考答案:
1.B
解:,,
, 故选项A错误;
,故选项B正确;
, 故选项C错误;
, 故选项D错误;
故选:B.
2.C
解:如图,在RtABC中,
∵,
∴设a=k,c=3k,
由勾股定理得:
∴.
故选:C.
3.D
解:∵,
∴.
∴.
故选:D.
4.B
解:连接AD交BC于点O,取AC中点N,连接ON,如图,
∵△ABC是等边三角形,
∴AB=AC=BC=8,∠ABC=60°,
∵△BCD是等腰三角形,
∴BD=DC,
∴AD垂直平分BC,
∴BO=CO=4,
∵AN=CN,
∴ON=AB=4,,
∵,
∴,
∴,
∴,
∴OD=AO,
∴tan∠ABO=,即,
∴,
∴OD=,
在Rt△BOD中,
,
故选:B.
5.C
解:观察图象可知,△ADB是等腰直角三角形,BD=AD=2,CD=1,
∴AB==2,AC==,
∴sinα=cosα=,故选项A正确;
tanC==2,故选项B正确;
tanα=1,故选项D正确;
∵sinβ==,cosβ=,∴sinβ≠cosβ,故选项C错误.
故选:C.
6.D
解:如图,连接OD,
∵四边形ABCD为菱形,
∴AD=CD=AB=10.
∵O是AC的中点,
∴OD⊥AC,OA=OCAC=6,
由勾股定理得,OD,
∵O、E分别是AC、AD的中点,
∴OE是△ACD的中位线,
∴OE∥CD,
∴∠AOE=∠ACD,
∴tan∠AOE=tan∠ACD,
故选:D.
7.A
解:∵弦的长是,弦的弦心距OC为6cm,
∴OC⊥AB,AC=CB=AB=6(cm),OC=6cm,∠AOC=∠BOC,
,
∴∠AOC=∠BOC=60°,即∠AOB=120°,
∴∠AEB=∠AOB =60°,
故选:A.
8.C
解:延长AD、BC,两线交于O,
在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB-BC=4-2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,
由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴,
∴,
解得:DC=,
故选:C.
9.D
解:∵EH∥CD,
∴△AEH∽△ACD.
∴,
∵AB=CD=4,BC=AD=5,
∴=.
设EH=4x,则AH=5x,
∴HG=GF=4x.
∵EF∥AD,
∴∠AFE=∠FAG,
∴tan∠AFE=tan∠FAG==.
故选:D.
10.D
解:
解:如图所示,设与x轴的另一个交点为D,连接CD,
∵,
∴是的直径,在中,,,
∴,
∴,
由圆周角定理可知,,
∴,
故选:D.
11.D
解:连接OC,作CM⊥x轴于M,AN⊥x轴于N,如图,
∵A、B两点为反比例函数与正比例函数的两交点,
∴点A、点B关于原点对称,
∴OA=OB,
∵CA=CB,
∴OC⊥AB,
在Rt△AOC中,tan∠CAO==2,
∵∠COM+∠AON=90°,∠AON+∠OAN=90°,
∴∠COM=∠OAN,
∴Rt△OCM∽Rt△AON,
∴4,
而S△OAN=×|3|=,
∴S△CMO=6,
∵|k|=6,
而k<0,
∴k=-12.
故选:D.
12.D
解:连接AF.
由作图可知,MN垂直平分线段AC,
∴FA=FC,
∵BF:FC=3:5,
∴可以假设BF=3k,CF=AF=5k,
∵∠B=90°,
∴AB,
∴BC=BF+CF=8k,
∴tan∠ACB,
故选:D.
13.60
解:∵α为锐角,且cosα=0.5,
∴角α的度数为60°.
故答案为:60.
14.3
解:连接DB,连接格点D、F交AB于F,如图,
由网格图可知,DB=DC,DB⊥DC,∠AEC=∠BED,
∵DFAC,
∴,
∴,
∴tan∠AEC=tan∠BED=3.
故答案为:3.
15.##
解:如图,过点C作CE⊥y轴于E,
∵A(2,0),B(0,6),
∴OA=2,OB=6,
在正方形ABCD中,AB=BC,∠ABC=90°,
∵∠ABO+∠CBE=90°,∠BCE+∠CBE=90°,
∴∠ABO=∠BCE,
在△ABO和△BCE中,
,
∴△ABO≌△BCE(AAS),
∴OA=BE=2,CE=OB=6,
∴OE=OB+BE=6+2=8,
在Rt△OCE中,,
∵CE⊥y轴,x轴⊥y轴,
∴CE∥x轴,
∴∠OCE=∠COA,
∴sin∠COA=sin∠OCE.
故答案为:.
16.
解:于,
,
,
可以假设,,则,
四边形是菱形,
,,
,
,
.
故答案为:.
17.
解:延长AO交⊙O于点D,连接CD,
∵BA与⊙O相切,
∴DA⊥AB,
∴∠DAC+∠BAC=90°,
∵AD为⊙O的直径,
∴∠ACD=90°,
∴∠DAC+∠D=90°,
∴∠D=∠BAC,
∵tan∠BAC=,
∴tanD=,即=,
∵AC=4,
∴CD=12,
由勾股定理得,AD===.
故答案为:.
18.(1) (2)
解:(1)
(2)
19.(1) (2)
解:(1)过点A作AH⊥BD于H,如图1所示:
∵Rt△ABC,∠BAC=90°,BC=6,AC=4,
∴AB===2,
∵AB AC=BC AH,
∴AH===,
∴BH===,
∵AH⊥BD,
∴BH=HD=,
∴BD=;
(2)过点D作DM⊥AC于M,如图2所示:
由(1)得:AH=,BD=,AB=2,
∴AD=AB=2,CD=BC﹣BD=6﹣=,
∵AH CD=DM AC,
∴DM===,
在Rt△ADM中,由勾股定理得:AM===,
∴cos∠DAC===.
20.(1)见解析 (2)
(1)
证明:连接OD,
∵CE⊥AC,
∴∠ACE=90°,
∴∠A+∠E=90°,
∵CD=CE,
∴∠E=∠CDE,
∴∠A+∠CDE=90°,
∵OA=OD,
∴∠A=∠ADO,
∴∠ADO+∠CDE=90°,
∴∠ODC=90°,
∴OD⊥DC,
∴DC与⊙O相切;
(2)
解:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
又∵∠BDC+∠ODB=90°,
∴∠BDC=∠A,
∵∠BCD=∠ACD,
∴△BCD∽△DCA,
∴,
∵tan∠BDC=tan∠A=,
设CB=x,则CD=2x,
∴CD2=CB CA,
∴,
∴x=,
∴CD=CE=.
21.(1)见解析 (2)3
证明:(1)如图,连接OD,
∵PD是切线,
∴OD⊥PD,
∴∠ODP=90°,
∴∠ODB+∠PDB=90°.
∵CD⊥BC,
∴∠CDB+∠DBC=90°.
∵OB=OD,
∴∠ODB=∠OBD,
∴∠CDB=∠PDB,
∴DB平分∠PDC.
(2)作BE⊥PD,如图.
∵DB平分∠PDC,BC⊥CD,BE⊥PD,
∴BC=BE.
在Rt△PDC中,,
∴PC=8,
∴.
设BC=x,则BE=x,PB=8-x.
∵∠EPB=∠CPD,
∴,
∴,
即,
解得x=3.
所以BC的长为3.
22.(1)见解析 (2) (3)
解:(1)如图1,∵,
∴,
∵四边形ABCD内接于,
∴,
∵,
∴,;
(2)如图2,作于F,
设,
∵AC为直径,
∴,,,
由(1)得,
∵,∴,,
∵,
∴;
(3)如图1,过B作于F,
设,,由(1)知
∵,
∴,
,,
∵,
∴,
,,,
∵,
∴,
即,即,
∵,
∴
答案第1页,共2页
