2021-2022学年苏科版数学九年级下册6.7用相似三角形解决问题课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学九年级下册6.7用相似三角形解决问题课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 743.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-28 23:46:58 | ||
图片预览

文档简介
用相似三角形解决问题
一、单选题
1.如图,某班上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子DA恰好与甲影子CA在同一条直线上,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙两同学相距( )米.
A.1 B.2 C.3 D.5
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
3.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
4.如图,身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时,发现自己在地面上的影子CE的长是2米,则路灯AB的高为( )
A.5米 B.6.4米 C.8米 D.10米
5.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度,标杆与旗杆的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,、、三点共线,则旗杆的高度为( )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
7.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB的长为30cm,且与水平桌面垂直,灯臂AC的长为10cm,灯头的横截面CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点.若不考虑其他因素,则该台灯在桌面可照亮的宽度BD的长为( )
A.90cm B.100cm C. D.
8.如图所示,为了测量文昌塔AB的高度,数学兴趣小组根据光的反射定理(图中),把一面镜子放在点C处,然后观测者沿着直线BC后退到点D.这时恰好在镜子里看到塔顶A,此时量得,,观测者目高,则塔AB的高度为( )
A.35m B.36m C.37m D.38m
9.如图,已知零件的外径,现用一个交叉卡钳(两条尺长和相等,)量零件的内孔直径,若,量的,则零件的厚度为( )
A. B. C. D.
10.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
11.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为米的竹竿的影长为米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为米,一级台阶高为米,如图所示,若此时落在地面上的影长为米,则树高为( )
A.11.5米 B.11.75米 C.11.8米 D.12.25米
12.如图,一人站在两等高的路灯之间走动,为人在路灯照射下的影子,为人在路灯照射下的影子.当人从点走向点时两段影子之和的变化趋势是( )
A.先变长后变短 B.先变短后变长
C.不变 D.先变短后变长再变短
二、填空题
13.图,小刚在打网球时,球恰好能打过网,且落在离网5m的位置上,则他的球拍击球的高度是___m.
14.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为_____m.
15.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,足分别为,,,,,则栏杆端应下降的垂直距离为________.
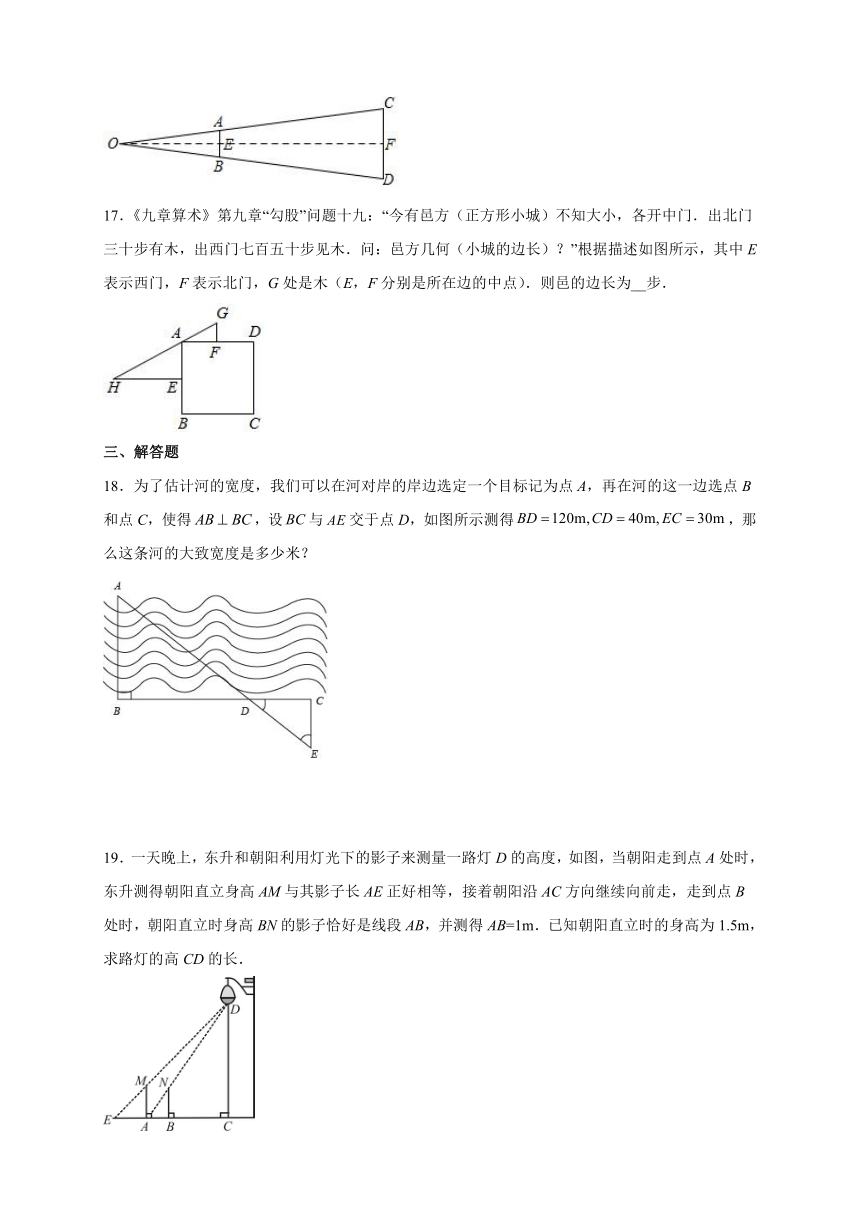
16.如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为______m.
17.《九章算术》第九章“勾股”问题十九:“今有邑方(正方形小城)不知大小,各开中门.出北门三十步有木,出西门七百五十步见木.问:邑方几何(小城的边长)?”根据描述如图所示,其中E表示西门,F表示北门,G处是木(E,F分别是所在边的中点).则邑的边长为__步.
三、解答题
18.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得,设与交于点D,如图所示测得,那么这条河的大致宽度是多少米?
19.一天晚上,东升和朝阳利用灯光下的影子来测量一路灯D的高度,如图,当朝阳走到点A处时,东升测得朝阳直立身高AM与其影子长AE正好相等,接着朝阳沿AC方向继续向前走,走到点B处时,朝阳直立时身高BN的影子恰好是线段AB,并测得AB=1m.已知朝阳直立时的身高为1.5m,求路灯的高CD的长.
20.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图,此时小亮的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直,已知装饰面的高度AD为0.66米.
(1)求证:;
(2)求装饰画顶部到墙壁的距离DC(精确到0.01米).
21.如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
22.如图,在Rt△ABC中,AC=3cm,BC=4cm,AB=5cm.动点E从点A出发,沿AB方向以1cm/s的速度向点B运动,同时动点F从点B出发,沿BC方向以1cm/s的速度向点C运动,连接CE,EF.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t(s)(0<t<4),请解答下列问题:
(1)当CE⊥AB时,求t的值;
(2)是否存在某一时刻t,使CE=CF,若存在,求出t的值;若不存在,请说明理由;
(3)设四边形AEFC的面积为ycm2,求y与t之间的关系式.
试卷第1页,共3页
参考答案:
1.A
解:设两个同学相距x米,
∵△ADE∽△ACB,
∴,
∴,
解得:x=1.
故选:A.
2.D
解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB//A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A′B′=6,
故选:D.
3.B
解:由题意得:
物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,
故选B
4.C
解:由题意知,CE=2米,CD=1.6米,BC=8米,CDAB,
则BE=BC+CE=10米,
∵CDAB,
∴△ECD∽△EBA
∴=,即=,
解得AB=8(米),即路灯的高AB为8米.
故选C.
5.A
解:设CD与EH交于点G
由题意得:EF=GD=BH=1.6,BD=EH=15,EG=DF=2
∴CG=CD-GD=1.4,
∵CD⊥FB,AB⊥FB,
∴CD∥AB,
∴△CGE∽△AHE,
∴,
即:,
∴AH=11.9,
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
故选:A.
6.C
解:由题意得:CB∥DF,
∴△ADF∽△ABC,
∴,
∵AD=3m,AB=5m,BC=b,
∴
∴DF=b ,
故选:C.
7.B
解:∵AC⊥AB,且AB=30cm,AC=10cm
∴由勾股定理得:
∵AC⊥AB,AB⊥BD
∴
∴∠ACB=∠CBD
∵∠CAB=∠ECF=90°
∴△BCD∽△CAB
∴
∴
故台灯在桌面可照亮的宽度BD的长为100cm.
故选B
8.B
解:∵入射角=反射角,
∴∠1=∠2,
∴∠ACB=90°-∠1=90°-∠2=∠ECD,
∵AB⊥BD,ED⊥BD,
∴∠ABC=∠EDC=90°,
∴△ABC∽△EDC,
∴
∵,, ,BC=BD-CD=94-4=90m,
∴,
解得m.
故选择B.
9.B
解:∵两条尺长AC和BD相等,OC=OD,
∴OA=OB,
∵OC:AC=1:3,
∴OC:OA=1:2,
∴OD:OB=OC:OA=1:2,
∵∠COD=∠AOB,
∴△AOB∽△COD,
∴CD:AB=OC:OA=1:2,
∵CD=10mm,
∴AB=20mm,
∴零件的厚度为mm.
故选:B
10.C
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
11.C
解:如图,根据题意可知EF=BC=4.4米,DE=0.2米,BE=FC=0.3米,则ED=4.6米,
∵同一时刻物高与影长成正比例,
∴AE:ED=1:0.4,即AE:4.6=1:0.4,
∴AE=11.5米,
∴AB=AE+EB=11.5+0.3=11.8米,
∴树的高度是11.8米,
故选C.
12.C
解:连接DF,已知CD=EF,CD⊥EG,EF⊥EG,
∴四边形CDFE为矩形.
∴DF∥GH,
∴
又AB∥CD,∴.
设=a,DF=b,
∴,
∴
∴
∴GH=,
∵a,b的长是定值不变,
∴当人从点走向点时两段影子之和不变.
故选:C.
13.2.4
解:∵DE∥BC,
∴△ADE∽△ACB,即,
则,
∴h=2.4m.
故答案为:2.4.
,
14.2.3
解:如图,过N点作于点D,
则四边形是矩形,
根据同一时刻木竿长和影子长的比是固定的,
∴,
∵,,,,
∴,
∴.
15.##m
解:,,
,
又,
,
则,
,,,
,
解得:,
栏杆端应下降的垂直距离为.
故答案为:.
16.200
解:∵AB∥CD,
∴△OAB∽△OCD,
∴,即,
∴.
故答案为:200.
17.300
解:设正方形城池的边长为x步,
由题意可得,Rt△AHE∽Rt△GAF,
∴=,
即,
解得,(不合题意,舍去),
答:正方形城池的边长为300步.
故答案为:300.
18.90m
解:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°
又∵∠ADB=∠EDC
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90(m),
即这条河的大致宽度是90m.
19.m
解:设长为m,
,,,,
,且为等腰直角三角形,
,
为等腰直角三角形,
m,m,
,
,,
,
,
,
解得:,
路灯的高度为m.
20.(1)证明见解析;(2)0.14米
解:(1)由题意可知∠DCA=∠BEA=∠CAB=90°
∵∠CAD+∠BAE=∠EBA+∠BAE
∴∠CAD=∠ABE
∴
(2)由(1)可得
其中AE=
则CD=.
21.3m
解:∵EO⊥BF,
∴∠FOE=90°,
∵AB⊥BF,CO⊥BF,
∴,
∴△ABD∽△COD,△ABF∽△EOF,
∴
∵OE=1m,CE=1.5m,OF=1.2m,OD=12m,
∴
整理得:
解得:AB=3.
答:围墙AB的高度是3m.
22.(1)t= (2)存在,,详解见解析 (3)
解:(1)当CE⊥AB时,可知∠AEC=90°,
∵AC=3,BC=4,AB=5,
∴△ABC的面积=×3×4=6,△ABC的面积=×5×CE,
∴×5×CE=6,
∴CE=,
在Rt△ACE中,AE=;
即t= ;
(2)过点C作CD⊥AB,垂足为D,
由题意可知AE=t,BF=t,
∵BC=4,
∴CF=4-t,
∵CE≥CD,即4-t≥,
∴t≤,
∴此时点E还未到D点,
由(1)可知CD=,
在Rt△CDE中,ED= ,
在Rt△ACD中,AD= ,
ED=AD-AE=,
,
两边同时平方,得:
,
整理得:
,
,
;
(3)过点E作EG⊥BC,垂足为G,
由图可知:四边形AEFC的面积=△ABC的面积-△BEF的面积,
∵AC⊥BC,EG⊥BC,
∴EG AC,
∴△BEG∽△BAC
∴ ,
即 ,
∴ ,
∴四边形AEFC的面积= ,
设四边形AEFC的面积为y,
∴ ,
∴ .
答案第1页,共2页
一、单选题
1.如图,某班上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子DA恰好与甲影子CA在同一条直线上,已知甲身高1.8米,乙身高1.5米,甲的影长是6米,则甲、乙两同学相距( )米.
A.1 B.2 C.3 D.5
2.如图,在直角坐标系中,点P(2,2)是一个光源.木杆AB两端的坐标分别为(0,1),(3,1).则木杆AB在x轴上的投影长为( )
A.3 B.4 C.5 D.6
3.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
4.如图,身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时,发现自己在地面上的影子CE的长是2米,则路灯AB的高为( )
A.5米 B.6.4米 C.8米 D.10米
5.为测量操场上悬挂国旗的旗杆的高度,设计的测量方案如图所示:标杆高度,标杆与旗杆的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,、、三点共线,则旗杆的高度为( )
A.13.5米 B.12.5米 C.11.9米 D.10.5米
6.如图,小明探究课本“综合与实践”板块“制作视力表”的相关内容:当测试距离为5m时,标准视力表中①号“E”字的高度BC长为b,当测试距离为3m时,②号“E”字的高度DF长为( )
A.5b B.3b C.b D.b
7.如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB的长为30cm,且与水平桌面垂直,灯臂AC的长为10cm,灯头的横截面CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点.若不考虑其他因素,则该台灯在桌面可照亮的宽度BD的长为( )
A.90cm B.100cm C. D.
8.如图所示,为了测量文昌塔AB的高度,数学兴趣小组根据光的反射定理(图中),把一面镜子放在点C处,然后观测者沿着直线BC后退到点D.这时恰好在镜子里看到塔顶A,此时量得,,观测者目高,则塔AB的高度为( )
A.35m B.36m C.37m D.38m
9.如图,已知零件的外径,现用一个交叉卡钳(两条尺长和相等,)量零件的内孔直径,若,量的,则零件的厚度为( )
A. B. C. D.
10.图1是装了液体的高脚杯示意图(数据如图),用去一部分液体后如图2所示,此时液面( )
A. B.
C. D.
11.兴趣小组的同学要测量树的高度.在阳光下,一名同学测得一根长为米的竹竿的影长为米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为米,一级台阶高为米,如图所示,若此时落在地面上的影长为米,则树高为( )
A.11.5米 B.11.75米 C.11.8米 D.12.25米
12.如图,一人站在两等高的路灯之间走动,为人在路灯照射下的影子,为人在路灯照射下的影子.当人从点走向点时两段影子之和的变化趋势是( )
A.先变长后变短 B.先变短后变长
C.不变 D.先变短后变长再变短
二、填空题
13.图,小刚在打网球时,球恰好能打过网,且落在离网5m的位置上,则他的球拍击球的高度是___m.
14.在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为_____m.
15.学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,足分别为,,,,,则栏杆端应下降的垂直距离为________.
16.如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF为______m.
17.《九章算术》第九章“勾股”问题十九:“今有邑方(正方形小城)不知大小,各开中门.出北门三十步有木,出西门七百五十步见木.问:邑方几何(小城的边长)?”根据描述如图所示,其中E表示西门,F表示北门,G处是木(E,F分别是所在边的中点).则邑的边长为__步.
三、解答题
18.为了估计河的宽度,我们可以在河对岸的岸边选定一个目标记为点A,再在河的这一边选点B和点C,使得,设与交于点D,如图所示测得,那么这条河的大致宽度是多少米?
19.一天晚上,东升和朝阳利用灯光下的影子来测量一路灯D的高度,如图,当朝阳走到点A处时,东升测得朝阳直立身高AM与其影子长AE正好相等,接着朝阳沿AC方向继续向前走,走到点B处时,朝阳直立时身高BN的影子恰好是线段AB,并测得AB=1m.已知朝阳直立时的身高为1.5m,求路灯的高CD的长.
20.我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图,此时小亮的眼睛与装饰画底部A处于同一水平线上,视线恰好落在装饰画中心位置E处,且与AD垂直,已知装饰面的高度AD为0.66米.
(1)求证:;
(2)求装饰画顶部到墙壁的距离DC(精确到0.01米).
21.如图,小丁家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间地面的D处,中午太阳光恰好能从窗户的最低点E射进房间地面的F处,AB⊥BD于点B,CE⊥BD于点O,小丁测得OE=1m,CE=1.5m,OF=1.2m,OD=12m,求围墙AB的高为多少米.
22.如图,在Rt△ABC中,AC=3cm,BC=4cm,AB=5cm.动点E从点A出发,沿AB方向以1cm/s的速度向点B运动,同时动点F从点B出发,沿BC方向以1cm/s的速度向点C运动,连接CE,EF.当其中一个点到达终点时,另一个点也随之停止运动.设运动时间为t(s)(0<t<4),请解答下列问题:
(1)当CE⊥AB时,求t的值;
(2)是否存在某一时刻t,使CE=CF,若存在,求出t的值;若不存在,请说明理由;
(3)设四边形AEFC的面积为ycm2,求y与t之间的关系式.
试卷第1页,共3页
参考答案:
1.A
解:设两个同学相距x米,
∵△ADE∽△ACB,
∴,
∴,
解得:x=1.
故选:A.
2.D
解:延长PA、PB分别交x轴于A′、B′,作PE⊥x轴于E,交AB于D,如图,
∵P(2,2),A(0,1),B(3,1).
∴PD=1,PE=2,AB=3,
∵AB//A′B′,
∴△PAB∽△PA′B′,
∴,即,
∴A′B′=6,
故选:D.
3.B
解:由题意得:
物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,
故选B
4.C
解:由题意知,CE=2米,CD=1.6米,BC=8米,CDAB,
则BE=BC+CE=10米,
∵CDAB,
∴△ECD∽△EBA
∴=,即=,
解得AB=8(米),即路灯的高AB为8米.
故选C.
5.A
解:设CD与EH交于点G
由题意得:EF=GD=BH=1.6,BD=EH=15,EG=DF=2
∴CG=CD-GD=1.4,
∵CD⊥FB,AB⊥FB,
∴CD∥AB,
∴△CGE∽△AHE,
∴,
即:,
∴AH=11.9,
∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).
故选:A.
6.C
解:由题意得:CB∥DF,
∴△ADF∽△ABC,
∴,
∵AD=3m,AB=5m,BC=b,
∴
∴DF=b ,
故选:C.
7.B
解:∵AC⊥AB,且AB=30cm,AC=10cm
∴由勾股定理得:
∵AC⊥AB,AB⊥BD
∴
∴∠ACB=∠CBD
∵∠CAB=∠ECF=90°
∴△BCD∽△CAB
∴
∴
故台灯在桌面可照亮的宽度BD的长为100cm.
故选B
8.B
解:∵入射角=反射角,
∴∠1=∠2,
∴∠ACB=90°-∠1=90°-∠2=∠ECD,
∵AB⊥BD,ED⊥BD,
∴∠ABC=∠EDC=90°,
∴△ABC∽△EDC,
∴
∵,, ,BC=BD-CD=94-4=90m,
∴,
解得m.
故选择B.
9.B
解:∵两条尺长AC和BD相等,OC=OD,
∴OA=OB,
∵OC:AC=1:3,
∴OC:OA=1:2,
∴OD:OB=OC:OA=1:2,
∵∠COD=∠AOB,
∴△AOB∽△COD,
∴CD:AB=OC:OA=1:2,
∵CD=10mm,
∴AB=20mm,
∴零件的厚度为mm.
故选:B
10.C
解:由题可知,第一个高脚杯盛液体的高度为:15-7=8(cm),
第二个高脚杯盛液体的高度为:11-7=4(cm),
因为液面都是水平的,图1和图2中的高脚杯是同一个高脚杯,
所以图1和图2中的两个三角形相似,
∴,
∴(cm),
故选:C.
11.C
解:如图,根据题意可知EF=BC=4.4米,DE=0.2米,BE=FC=0.3米,则ED=4.6米,
∵同一时刻物高与影长成正比例,
∴AE:ED=1:0.4,即AE:4.6=1:0.4,
∴AE=11.5米,
∴AB=AE+EB=11.5+0.3=11.8米,
∴树的高度是11.8米,
故选C.
12.C
解:连接DF,已知CD=EF,CD⊥EG,EF⊥EG,
∴四边形CDFE为矩形.
∴DF∥GH,
∴
又AB∥CD,∴.
设=a,DF=b,
∴,
∴
∴
∴GH=,
∵a,b的长是定值不变,
∴当人从点走向点时两段影子之和不变.
故选:C.
13.2.4
解:∵DE∥BC,
∴△ADE∽△ACB,即,
则,
∴h=2.4m.
故答案为:2.4.
,
14.2.3
解:如图,过N点作于点D,
则四边形是矩形,
根据同一时刻木竿长和影子长的比是固定的,
∴,
∵,,,,
∴,
∴.
15.##m
解:,,
,
又,
,
则,
,,,
,
解得:,
栏杆端应下降的垂直距离为.
故答案为:.
16.200
解:∵AB∥CD,
∴△OAB∽△OCD,
∴,即,
∴.
故答案为:200.
17.300
解:设正方形城池的边长为x步,
由题意可得,Rt△AHE∽Rt△GAF,
∴=,
即,
解得,(不合题意,舍去),
答:正方形城池的边长为300步.
故答案为:300.
18.90m
解:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°
又∵∠ADB=∠EDC
∴△ABD∽△ECD,
∴AB:CE=BD:CD,
即AB:30=120:40,
∴AB=90(m),
即这条河的大致宽度是90m.
19.m
解:设长为m,
,,,,
,且为等腰直角三角形,
,
为等腰直角三角形,
m,m,
,
,,
,
,
,
解得:,
路灯的高度为m.
20.(1)证明见解析;(2)0.14米
解:(1)由题意可知∠DCA=∠BEA=∠CAB=90°
∵∠CAD+∠BAE=∠EBA+∠BAE
∴∠CAD=∠ABE
∴
(2)由(1)可得
其中AE=
则CD=.
21.3m
解:∵EO⊥BF,
∴∠FOE=90°,
∵AB⊥BF,CO⊥BF,
∴,
∴△ABD∽△COD,△ABF∽△EOF,
∴
∵OE=1m,CE=1.5m,OF=1.2m,OD=12m,
∴
整理得:
解得:AB=3.
答:围墙AB的高度是3m.
22.(1)t= (2)存在,,详解见解析 (3)
解:(1)当CE⊥AB时,可知∠AEC=90°,
∵AC=3,BC=4,AB=5,
∴△ABC的面积=×3×4=6,△ABC的面积=×5×CE,
∴×5×CE=6,
∴CE=,
在Rt△ACE中,AE=;
即t= ;
(2)过点C作CD⊥AB,垂足为D,
由题意可知AE=t,BF=t,
∵BC=4,
∴CF=4-t,
∵CE≥CD,即4-t≥,
∴t≤,
∴此时点E还未到D点,
由(1)可知CD=,
在Rt△CDE中,ED= ,
在Rt△ACD中,AD= ,
ED=AD-AE=,
,
两边同时平方,得:
,
整理得:
,
,
;
(3)过点E作EG⊥BC,垂足为G,
由图可知:四边形AEFC的面积=△ABC的面积-△BEF的面积,
∵AC⊥BC,EG⊥BC,
∴EG AC,
∴△BEG∽△BAC
∴ ,
即 ,
∴ ,
∴四边形AEFC的面积= ,
设四边形AEFC的面积为y,
∴ ,
∴ .
答案第1页,共2页
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
