4.3 相似多边形 课件(共25张PPT )
文档属性
| 名称 | 4.3 相似多边形 课件(共25张PPT ) |  | |
| 格式 | pptx | ||
| 文件大小 | 961.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 14:07:30 | ||
图片预览



文档简介
(共25张PPT)
3 相似多边形
北师版九年级上册
新课导入
B
C
A
D
E
F
请找出形状相同的图形.
新课导入
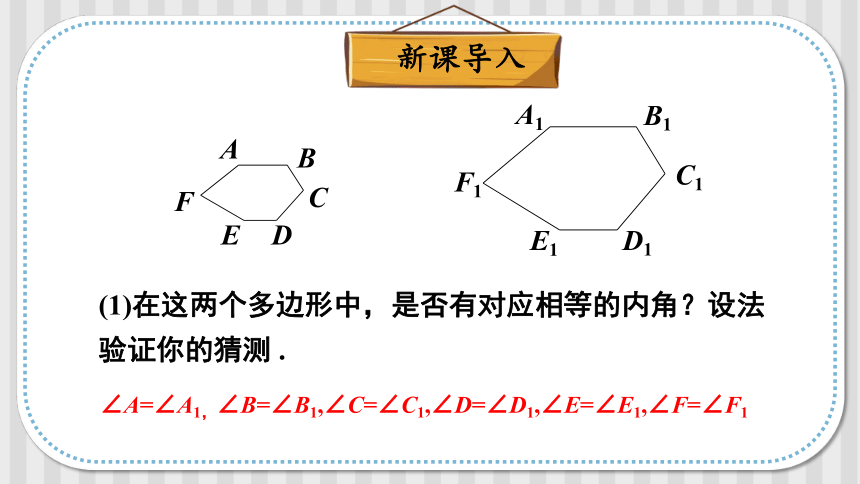
(1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜测 .
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,∠F=∠F1
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
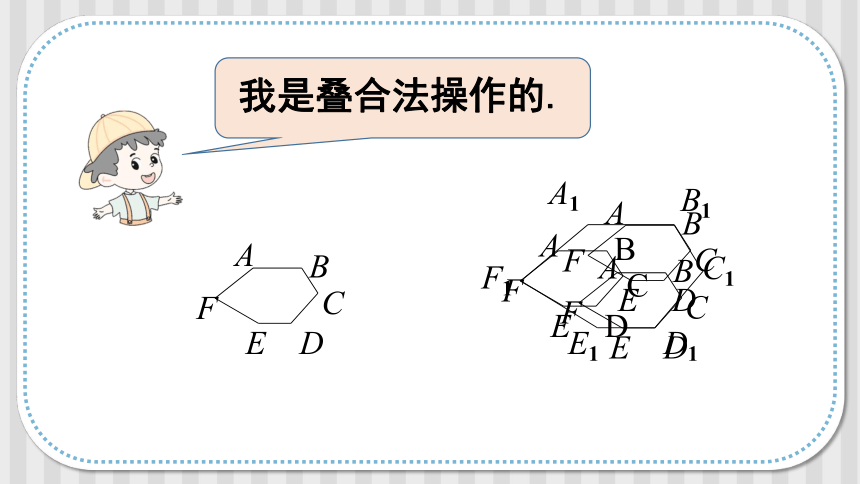
我是叠合法操作的.
A
B
C
F
A1
B1
C1
F1
D
E
D1
E1
A=
B=
C=
D=
E=
F=
A1=
B1=
C1=
D1=
E1=
F1=
——
——
——
——
——
——
——
——
——
——
——
——
AB=
BC=
CD=
DE=
EF=
FA=
A1B1=
B1C1=
C1D1=
D1E1=
E1F1=
F1A1=
——
——
——
——
——
——
——
——
——
——
——
——
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
6.5
5.5
6
5
7.5
4.5
13
11
12
10
15
9
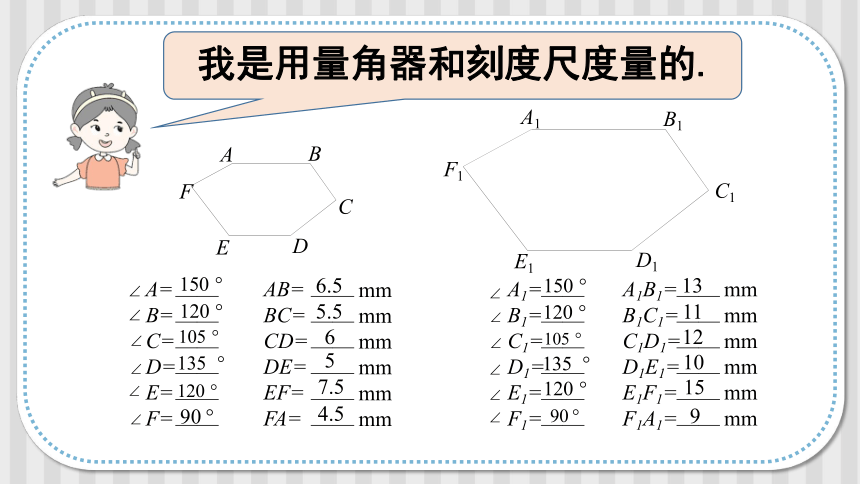
我是用量角器和刻度尺度量的.
从以上数据,你能发现对应边的关系吗 ?
A= A1
B= B1
C= C1
D= D1
E= E1
F= F1
对应角
对应边
A=
B=
C=
D=
E=
F=
A1=
B1=
C1=
D1=
E1=
F1=
——
——
——
——
——
——
——
——
——
——
——
——
AB=
BC=
CD=
DE=
EF=
FA=
A1B1=
B1C1=
C1D1=
D1E1=
E1F1=
F1A1=
——
——
——
——
——
——
——
——
——
——
——
——
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
6.5
5.5
6
5
7.5
4.5
13
11
12
10
15
9
A
B
C
F
A1
B1
C1
F1
D
E
D1
E1
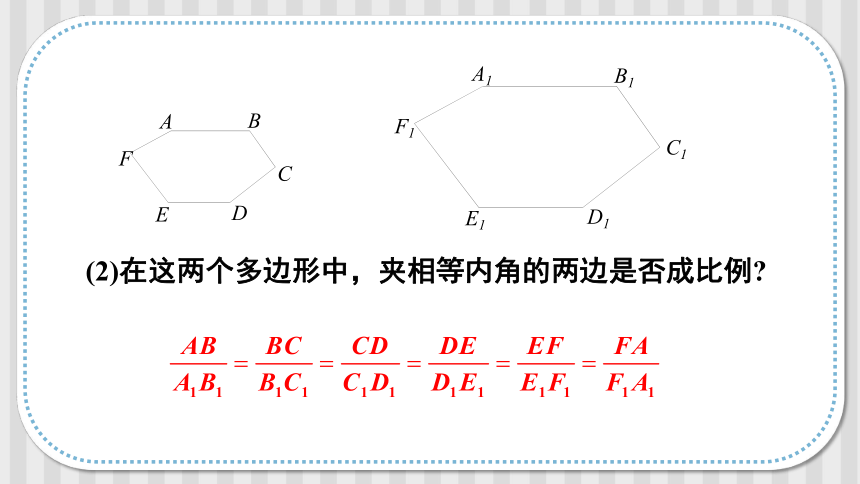
(2)在这两个多边形中,夹相等内角的两边是否成比例
各角分别相等、各边成比例的两个多边形叫做相似多边形.六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1 ,“∽”读作“相似于”.其中∠A与∠A1, ∠B与∠B1, ∠C与∠C1, ∠D与∠D1, ∠E与∠E1, ∠F与∠F1分别相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1, DE与D1E1,EF与E1F1,FA与F1A1的比都相等,称为对应边.
结论
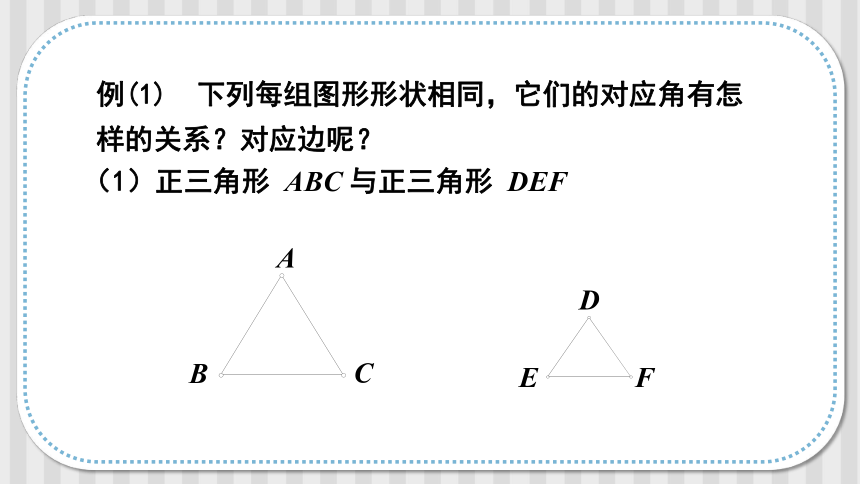
例(1) 下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形 ABC 与正三角形 DEF
A
B
C
D
E
F
(1)由于正三角形每个角等于 ,
所以
由于正三角形三边相等,
所以
解:
A
B
C
D
E
F
(2)正方形ABCD与正方形EFGH.
B
C
D
E
F
A
(2)
H
G
解:(2)由于正方形每个角都是直角,所以
∠A=∠E= 90°,∠B=∠F= 90°,
∠C=∠G= 90°,∠D=∠H= 90 °;
由于正方形四边相等,所以
记作如:六边形ABCDEF∽六边形A1B1C1D1E1F1
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
注意:记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
归纳总结
想一想
(1)任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
(2)任意两个菱形相似吗
相似
不相似
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
做一做
A
D
(3+0.075 2)m = 3.15 m
直观有时是不可靠的
1.5︰3 ≠ 1.65︰3.15
A
B
C
D
E
F
G
H
3m
(1.5+0.075 2)m = 1.65m
1.5m
A
B
C
D
达标检测
【选自教材P88 随堂练习 第1题】
1.图中每组两个矩形相似吗?说说你的理由。
2
3
2
3
3
4.5
2.5
6
(1)
(2)
达标检测
2.如图,一个矩形广场的长为60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为 x m,那么当 x 为多少时,小路内外边缘所围成的两个矩形相似?
【选自教材P88 随堂练习 第2题】
3.如图,矩形ABCD∽矩形EFGH,它们的相似比是2:3,已知 AB = 3 cm,BC = 5 cm,求EF,FG的长 .
A
B
C
D
E
F
G
H
【选自教材P88 习题4.4】
达标检测
A
B
C
D
E
F
G
H
达标检测
4.在菱形ABCD与菱形EFGH中,∠A= ∠E,这两个菱形相似吗,为什么?
【选自教材P88 习题4.4】
解:∵在菱形ABCD与菱形EFGH中,设∠A=∠E=α,
∴∠C=∠G=α,∠B=∠F=180°- α,∠D=∠H=180°- α,
即菱形ABCD与菱形EFGH的对应角相等;
又∵菱形的四条边都相等,
∴两菱形的对应边成比例,
即菱形ABCD与菱形EFGH的对应边的比相等,
∴菱形ABCD与菱形相似.
达标检测
【选自教材P88 习题4.4】
5.以正方形各边中点为顶点,可以组成一个新正方形,求新正方形与原正方形的相似比.
解:如图,设正方形ABCD的边长为2a,
∵E、F、G、H分别为正方形ABCD各边的中点,
∴AE = AH = a,
∵∠A = 90,
∴EH =
∴新正方形与原正方形的相似比 =EH∶AB= .
6.现有大小相同的正方形纸片30张,小亮用其中3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她至少要用几张正方形纸片(不得把每个正方形纸片剪开) 你知道她可能拼出什么样的图形吗 请你试着画一画.
达标检测
【选自教材P88 习题4.4】
达标检测
解:∵正方形纸片大小相同,
∴拼一个与它形状相同但比它大的长方形,至少长和宽各是原来的2倍,
∴需要正方形的纸片是3×2×(1×2)=12张.
拼图如下:
课堂小结
1.各对应角相等、各对应边成比例的两个多边形叫做相似多边形
4.如果两个多边形不相似,那么它们的各角可能对应相等,它们的各边可能对应成比例.
2.相似比与叙述的顺序有关.
3.相似多边形的对应角相等,对应边成比例.
完成练习册本课时的习题。
课后作业
3 相似多边形
北师版九年级上册
新课导入
B
C
A
D
E
F
请找出形状相同的图形.
新课导入
(1)在这两个多边形中,是否有对应相等的内角?设法验证你的猜测 .
∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,∠E=∠E1,∠F=∠F1
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B1
C1
D1
E1
F1
A1
B
C
D
E
F
A
B
C
D
E
F
A
B
C
D
E
F
A
我是叠合法操作的.
A
B
C
F
A1
B1
C1
F1
D
E
D1
E1
A=
B=
C=
D=
E=
F=
A1=
B1=
C1=
D1=
E1=
F1=
——
——
——
——
——
——
——
——
——
——
——
——
AB=
BC=
CD=
DE=
EF=
FA=
A1B1=
B1C1=
C1D1=
D1E1=
E1F1=
F1A1=
——
——
——
——
——
——
——
——
——
——
——
——
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
6.5
5.5
6
5
7.5
4.5
13
11
12
10
15
9
我是用量角器和刻度尺度量的.
从以上数据,你能发现对应边的关系吗 ?
A= A1
B= B1
C= C1
D= D1
E= E1
F= F1
对应角
对应边
A=
B=
C=
D=
E=
F=
A1=
B1=
C1=
D1=
E1=
F1=
——
——
——
——
——
——
——
——
——
——
——
——
AB=
BC=
CD=
DE=
EF=
FA=
A1B1=
B1C1=
C1D1=
D1E1=
E1F1=
F1A1=
——
——
——
——
——
——
——
——
——
——
——
——
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
mm
6.5
5.5
6
5
7.5
4.5
13
11
12
10
15
9
A
B
C
F
A1
B1
C1
F1
D
E
D1
E1
(2)在这两个多边形中,夹相等内角的两边是否成比例
各角分别相等、各边成比例的两个多边形叫做相似多边形.六边形ABCDEF与六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1 ,“∽”读作“相似于”.其中∠A与∠A1, ∠B与∠B1, ∠C与∠C1, ∠D与∠D1, ∠E与∠E1, ∠F与∠F1分别相等,称为对应角;AB与A1B1,BC与B1C1,CD与C1D1, DE与D1E1,EF与E1F1,FA与F1A1的比都相等,称为对应边.
结论
例(1) 下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(1)正三角形 ABC 与正三角形 DEF
A
B
C
D
E
F
(1)由于正三角形每个角等于 ,
所以
由于正三角形三边相等,
所以
解:
A
B
C
D
E
F
(2)正方形ABCD与正方形EFGH.
B
C
D
E
F
A
(2)
H
G
解:(2)由于正方形每个角都是直角,所以
∠A=∠E= 90°,∠B=∠F= 90°,
∠C=∠G= 90°,∠D=∠H= 90 °;
由于正方形四边相等,所以
记作如:六边形ABCDEF∽六边形A1B1C1D1E1F1
各对应角相等、各对应边成比例的两个多边形叫做相似多边形.
注意:记两个多边形相似时,要把表示对应顶点的字母写在对应的位置上.
归纳总结
想一想
(1)任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢?
(2)任意两个菱形相似吗
相似
不相似
一块长3m、宽1.5m的矩形黑板如下图所示,镶在其外围的木质边框宽7.5cm。边框的内外边缘所成的矩形相似吗?为什么?
做一做
A
D
(3+0.075 2)m = 3.15 m
直观有时是不可靠的
1.5︰3 ≠ 1.65︰3.15
A
B
C
D
E
F
G
H
3m
(1.5+0.075 2)m = 1.65m
1.5m
A
B
C
D
达标检测
【选自教材P88 随堂练习 第1题】
1.图中每组两个矩形相似吗?说说你的理由。
2
3
2
3
3
4.5
2.5
6
(1)
(2)
达标检测
2.如图,一个矩形广场的长为60 m,宽为40 m,广场内两条纵向小路的宽均为1.5 m,如果设两条横向小路的宽都为 x m,那么当 x 为多少时,小路内外边缘所围成的两个矩形相似?
【选自教材P88 随堂练习 第2题】
3.如图,矩形ABCD∽矩形EFGH,它们的相似比是2:3,已知 AB = 3 cm,BC = 5 cm,求EF,FG的长 .
A
B
C
D
E
F
G
H
【选自教材P88 习题4.4】
达标检测
A
B
C
D
E
F
G
H
达标检测
4.在菱形ABCD与菱形EFGH中,∠A= ∠E,这两个菱形相似吗,为什么?
【选自教材P88 习题4.4】
解:∵在菱形ABCD与菱形EFGH中,设∠A=∠E=α,
∴∠C=∠G=α,∠B=∠F=180°- α,∠D=∠H=180°- α,
即菱形ABCD与菱形EFGH的对应角相等;
又∵菱形的四条边都相等,
∴两菱形的对应边成比例,
即菱形ABCD与菱形EFGH的对应边的比相等,
∴菱形ABCD与菱形相似.
达标检测
【选自教材P88 习题4.4】
5.以正方形各边中点为顶点,可以组成一个新正方形,求新正方形与原正方形的相似比.
解:如图,设正方形ABCD的边长为2a,
∵E、F、G、H分别为正方形ABCD各边的中点,
∴AE = AH = a,
∵∠A = 90,
∴EH =
∴新正方形与原正方形的相似比 =EH∶AB= .
6.现有大小相同的正方形纸片30张,小亮用其中3张拼成一个如图所示的长方形,小芳也想拼一个与它形状相同但比它大的长方形,则她至少要用几张正方形纸片(不得把每个正方形纸片剪开) 你知道她可能拼出什么样的图形吗 请你试着画一画.
达标检测
【选自教材P88 习题4.4】
达标检测
解:∵正方形纸片大小相同,
∴拼一个与它形状相同但比它大的长方形,至少长和宽各是原来的2倍,
∴需要正方形的纸片是3×2×(1×2)=12张.
拼图如下:
课堂小结
1.各对应角相等、各对应边成比例的两个多边形叫做相似多边形
4.如果两个多边形不相似,那么它们的各角可能对应相等,它们的各边可能对应成比例.
2.相似比与叙述的顺序有关.
3.相似多边形的对应角相等,对应边成比例.
完成练习册本课时的习题。
课后作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
