4.5 相似三角形判定定理的证明 课件 (共19张PPT)
文档属性
| 名称 | 4.5 相似三角形判定定理的证明 课件 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
5 相似三角形判 定定理的证明
北师版九年级上册
复习导入
判定两个三角形相似的方法有哪些?
你能对它们进行证明吗?
探究新知
A
B
C
A′
B′
C′
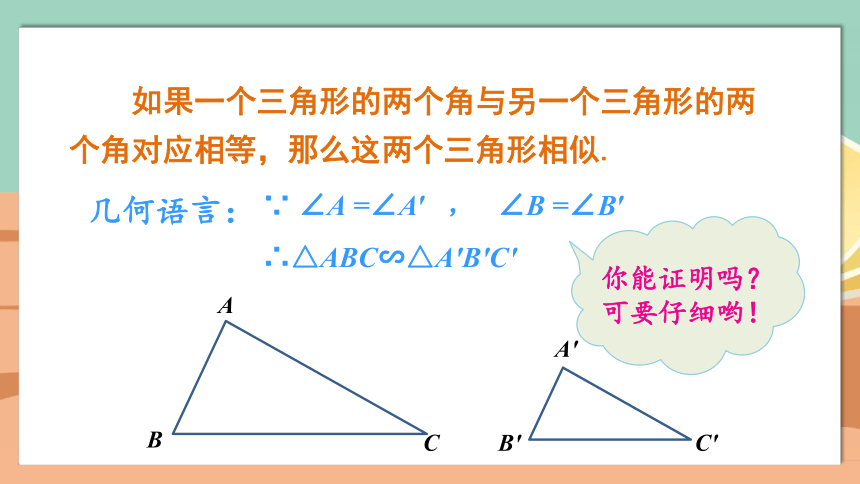
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
∵ ∠A =∠A′ , ∠B =∠B′
∴△ABC∽△A′B′C′
几何语言:
你能证明吗?
可要仔细哟!
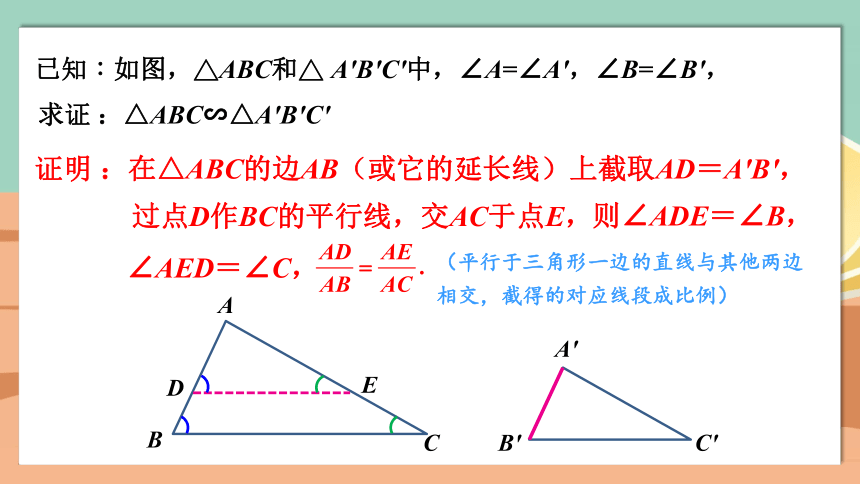
已知:如图,△ABC和△ A′B′C′中,∠A=∠A′,∠B=∠B′,
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
过点D作BC的平行线,交AC于点E,
则∠ADE=∠B,
∠AED=∠C,
(平行于三角形一边的直线与其他两边相交,截得的对应线段成比例)
F
A
B
C
A′
B′
C′
D
E
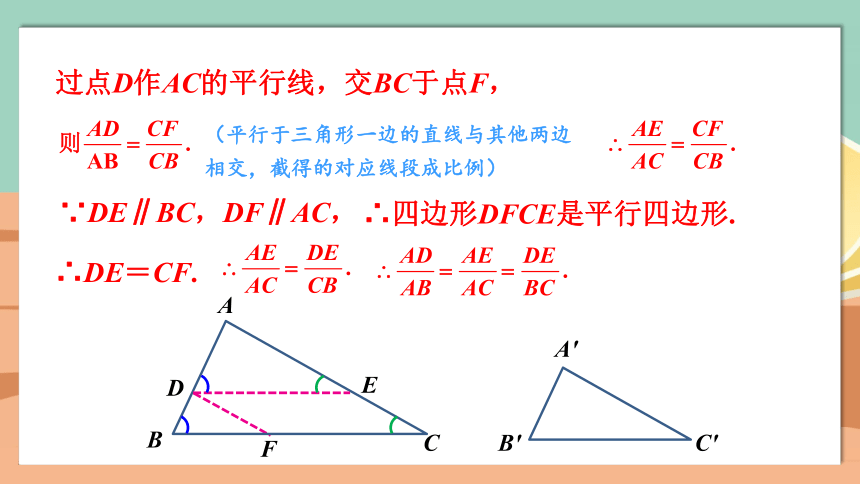
过点D作AC的平行线,交BC于点F,
(平行于三角形一边的直线与其他两边相交,截得的对应线段成比例)
∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形.
∴DE=CF.
F
A
B
C
A′
B′
C′
D
E
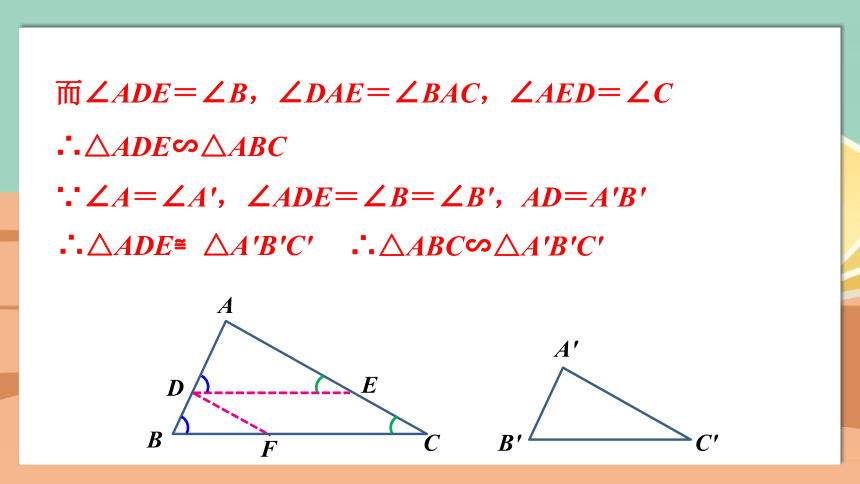
而∠ADE=∠B,∠DAE=∠BAC,∠AED=∠C
∴△ADE∽△ABC
∵∠A=∠A′,∠ADE=∠B=∠B′,AD=A′B′
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
探究新知
A
B
C
A′
B′
C′
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
几何语言:
你能证明吗?
可要仔细哟!
∵∠A =∠A′ ,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
过点D作BC的平行线,交AC于点E,
则∠B=∠ADE,
∠C=∠AED,
已知:如图,△ABC和△ A′B′C′中,∠A=∠A′,
∴△ABC∽△ADE
(两角分别相等的两个三角形相似)
A
B
C
A′
B′
C′
D
E
而∠A=∠A′,
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
探究新知
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
几何语言:
你要如何
证明呢?
∴△ABC∽△A′B′C′
∵
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
AE=A′C′
连接DE.
已知:如图,△ABC和△ A′B′C′中,
A
B
C
A′
B′
C′
D
E
而∠BAC=∠DAE,
∴△ABC∽△ADE
(两边成比例且夹角相等的两个三角形相似)
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
随堂练习
1. 如图,在等边三角形ABC中,D,E,F分别是三边上的点,AE=BF=CD,那么△ABC与△DEF相似吗?请证明你的结论.
C
A
B
E
D
F
△ABC∽△DEF
证明:等边三角形ABC中, AE=BF=CD
则BE=CF=AD,∠A=∠B=∠C
∴△AED≌△BFE≌△CDF
∴DE=DF=EF
∴△EFD是等边三角形
∴∠EDF=∠A=60°,∠EFD=∠B=60°
∴△ABC∽△DEF
2. 已知:如图, 求证:AB=AE.
A
B
D
E
C
证明:
∴△ADE∽△CAB
∴∠B=∠AEB
∴AB=AE
课堂小结
通过本节课的学习,你有哪些收获?
课后作业
完成本课时相关课时作业
5 相似三角形判 定定理的证明
北师版九年级上册
复习导入
判定两个三角形相似的方法有哪些?
你能对它们进行证明吗?
探究新知
A
B
C
A′
B′
C′
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
∵ ∠A =∠A′ , ∠B =∠B′
∴△ABC∽△A′B′C′
几何语言:
你能证明吗?
可要仔细哟!
已知:如图,△ABC和△ A′B′C′中,∠A=∠A′,∠B=∠B′,
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
过点D作BC的平行线,交AC于点E,
则∠ADE=∠B,
∠AED=∠C,
(平行于三角形一边的直线与其他两边相交,截得的对应线段成比例)
F
A
B
C
A′
B′
C′
D
E
过点D作AC的平行线,交BC于点F,
(平行于三角形一边的直线与其他两边相交,截得的对应线段成比例)
∵DE∥BC,DF∥AC,
∴四边形DFCE是平行四边形.
∴DE=CF.
F
A
B
C
A′
B′
C′
D
E
而∠ADE=∠B,∠DAE=∠BAC,∠AED=∠C
∴△ADE∽△ABC
∵∠A=∠A′,∠ADE=∠B=∠B′,AD=A′B′
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
探究新知
A
B
C
A′
B′
C′
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
几何语言:
你能证明吗?
可要仔细哟!
∵∠A =∠A′ ,
∴△ABC∽△A′B′C′
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
过点D作BC的平行线,交AC于点E,
则∠B=∠ADE,
∠C=∠AED,
已知:如图,△ABC和△ A′B′C′中,∠A=∠A′,
∴△ABC∽△ADE
(两角分别相等的两个三角形相似)
A
B
C
A′
B′
C′
D
E
而∠A=∠A′,
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
探究新知
如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
几何语言:
你要如何
证明呢?
∴△ABC∽△A′B′C′
∵
A
B
C
A′
B′
C′
A
B
C
A′
B′
C′
求证 :△ABC∽△A'B'C'
D
E
证明 :在△ABC的边AB(或它的延长线)上截取AD=A′B′,
AE=A′C′
连接DE.
已知:如图,△ABC和△ A′B′C′中,
A
B
C
A′
B′
C′
D
E
而∠BAC=∠DAE,
∴△ABC∽△ADE
(两边成比例且夹角相等的两个三角形相似)
∴△ADE≌△A′B′C′
∴△ABC∽△A'B'C'
随堂练习
1. 如图,在等边三角形ABC中,D,E,F分别是三边上的点,AE=BF=CD,那么△ABC与△DEF相似吗?请证明你的结论.
C
A
B
E
D
F
△ABC∽△DEF
证明:等边三角形ABC中, AE=BF=CD
则BE=CF=AD,∠A=∠B=∠C
∴△AED≌△BFE≌△CDF
∴DE=DF=EF
∴△EFD是等边三角形
∴∠EDF=∠A=60°,∠EFD=∠B=60°
∴△ABC∽△DEF
2. 已知:如图, 求证:AB=AE.
A
B
D
E
C
证明:
∴△ADE∽△CAB
∴∠B=∠AEB
∴AB=AE
课堂小结
通过本节课的学习,你有哪些收获?
课后作业
完成本课时相关课时作业
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
