华东师大版数学七年级下册 9.1 三角形中内、外角的有关计算专题课件 (共16张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 9.1 三角形中内、外角的有关计算专题课件 (共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 11:52:26 | ||
图片预览





文档简介
(共16张PPT)
数学 七年级下册 华师版
专题课堂(九) 三角形中内、外角的有关计算
第9章 多边形
【例1】 如图,平面上直线a,b分别过线段OK的两端点,
则a,b相交所成的锐角是( )
A.20° B.30° C.70° D.80°
B
【对应训练】
1.如图,CD,BE相交于点A,若∠B=70°,∠DAE=60°,则∠C=____°.
50
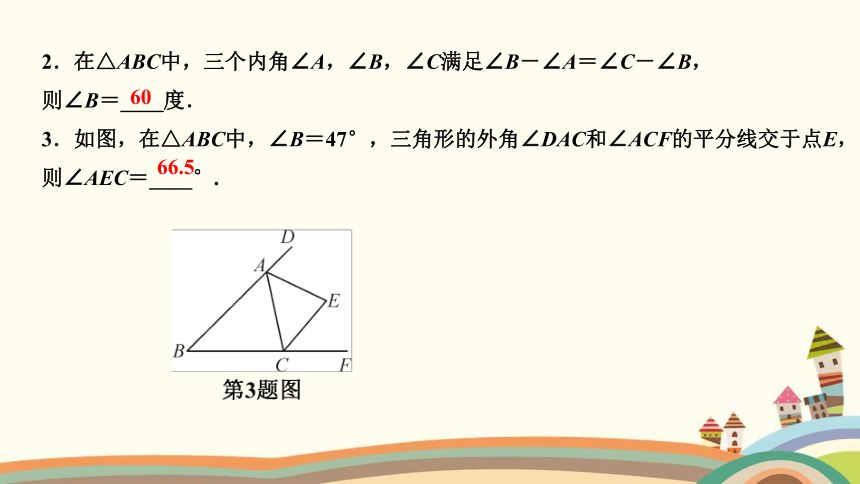
2.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,
则∠B=____度.
3.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,
则∠AEC=____°.
60
66.5
【例2】 (永州中考)一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=____.
75°
【对应训练】
4.如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上.
如果∠2=60°,那么∠1的度数为( )
A.60° B.50° C.40° D.30°
5.(2021·毕节)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
D
B
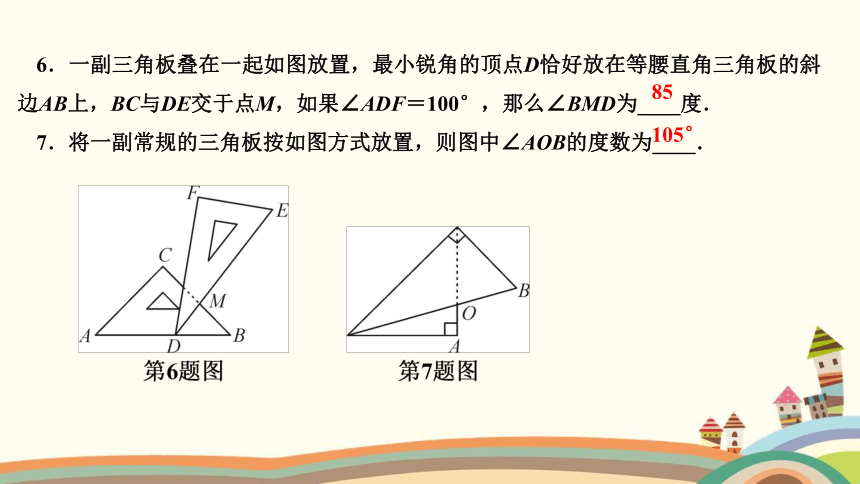
6.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M,如果∠ADF=100°,那么∠BMD为____度.
7.将一副常规的三角板按如图方式放置,则图中∠AOB的度数为____.
85
105°
8.将一副三角板如图所示摆放,则∠AOB=____.
9.如图,一副三角板按如图叠放在一起,则图中∠α的度数为____.
165°
75°
10.一副三角板按如图方式摆放,若∠1=33°,求∠2的度数.
解:∵∠1=33°,∴∠3=90°-33°=57°,∴∠4=∠3=57°,
∴∠5=180°-57°-45°=78°,∴∠2=∠5=78°
【例3】 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
A.80° B.85° C.90° D.95°
【对应训练】
11.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
A.105° B.110° C.115° D.120°
B
C
12.如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,
则∠D=____.
13.如图,a∥b,∠1+∠2=75°,则∠3+∠4=____.
48°
105°
14.如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
解:∵BD是∠ABC的平分线,∴∠ABD=∠CBD.∵DE∥BC,∴∠CBD=∠BDE,∴∠EBD=∠BDE.∵∠BDC是△ABD的外角,∴∠A+∠ABD=∠BDC,∴∠EBD=∠BDC-∠A=95°-60°=35°,∴∠BDE=35°,∴∠BED=180°-∠EBD-∠BDE=180°-35°-35°=110°
15.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)判断图中的FC和AB有怎样的位置关系?并说明理由.
(2)计算图中∠DFC的度数.
解:(1)FC∥AB,理由是:∵△ACB是等腰直角三角形,∴∠3=∠B=45°,∵∠DCE=90°,CF平分∠DCE,∴∠1=∠2=45°,∴∠1=∠3,∴FC∥AB
(2)∵∠2=45°,∠E=60°,∴∠DFC=∠2+∠E=45°+60°=105°
【例4】 如图,在△ABC中,∠C=60°,若沿图中虚线截去∠C,
则∠1+∠2等于( )
A.360° B.240° C.180° D.140°
【对应训练】
16.(聊城中考)如图,将一张三角形纸片ABC的一角折叠,
使点A落在△ABC外的A′处,折痕为DE.如果∠A=α,∠CEA′=β,
∠BDA′=γ,那么下列式子中正确的是( )
A. γ=2α+β B. γ=α+2β
C. γ=α+β D. γ=180°-α-β
B
A
17.如图,在Rt△ABC中,∠ACB=90°,∠A=52°,
将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=____.
14°
数学 七年级下册 华师版
专题课堂(九) 三角形中内、外角的有关计算
第9章 多边形
【例1】 如图,平面上直线a,b分别过线段OK的两端点,
则a,b相交所成的锐角是( )
A.20° B.30° C.70° D.80°
B
【对应训练】
1.如图,CD,BE相交于点A,若∠B=70°,∠DAE=60°,则∠C=____°.
50
2.在△ABC中,三个内角∠A,∠B,∠C满足∠B-∠A=∠C-∠B,
则∠B=____度.
3.如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,
则∠AEC=____°.
60
66.5
【例2】 (永州中考)一副透明的三角板,如图叠放,直角三角板的斜边AB,CE相交于点D,则∠BDC=____.
75°
【对应训练】
4.如图,将一块含有30°角的直角三角板的两个顶点放在长方形直尺的一组对边上.
如果∠2=60°,那么∠1的度数为( )
A.60° B.50° C.40° D.30°
5.(2021·毕节)将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
A.70° B.75° C.80° D.85°
D
B
6.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M,如果∠ADF=100°,那么∠BMD为____度.
7.将一副常规的三角板按如图方式放置,则图中∠AOB的度数为____.
85
105°
8.将一副三角板如图所示摆放,则∠AOB=____.
9.如图,一副三角板按如图叠放在一起,则图中∠α的度数为____.
165°
75°
10.一副三角板按如图方式摆放,若∠1=33°,求∠2的度数.
解:∵∠1=33°,∴∠3=90°-33°=57°,∴∠4=∠3=57°,
∴∠5=180°-57°-45°=78°,∴∠2=∠5=78°
【例3】 如图,直线AB∥CD,∠A=40°,∠D=45°,则∠1的度数是( )
A.80° B.85° C.90° D.95°
【对应训练】
11.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
A.105° B.110° C.115° D.120°
B
C
12.如图,AB∥CD,AE交CD于点C,DE⊥AE于点E,若∠A=42°,
则∠D=____.
13.如图,a∥b,∠1+∠2=75°,则∠3+∠4=____.
48°
105°
14.如图,在△ABC中,BD是∠ABC的平分线,DE∥BC,交AB于点E,∠A=60°,∠BDC=95°,求△BDE各内角的度数.
解:∵BD是∠ABC的平分线,∴∠ABD=∠CBD.∵DE∥BC,∴∠CBD=∠BDE,∴∠EBD=∠BDE.∵∠BDC是△ABD的外角,∴∠A+∠ABD=∠BDC,∴∠EBD=∠BDC-∠A=95°-60°=35°,∴∠BDE=35°,∴∠BED=180°-∠EBD-∠BDE=180°-35°-35°=110°
15.将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)判断图中的FC和AB有怎样的位置关系?并说明理由.
(2)计算图中∠DFC的度数.
解:(1)FC∥AB,理由是:∵△ACB是等腰直角三角形,∴∠3=∠B=45°,∵∠DCE=90°,CF平分∠DCE,∴∠1=∠2=45°,∴∠1=∠3,∴FC∥AB
(2)∵∠2=45°,∠E=60°,∴∠DFC=∠2+∠E=45°+60°=105°
【例4】 如图,在△ABC中,∠C=60°,若沿图中虚线截去∠C,
则∠1+∠2等于( )
A.360° B.240° C.180° D.140°
【对应训练】
16.(聊城中考)如图,将一张三角形纸片ABC的一角折叠,
使点A落在△ABC外的A′处,折痕为DE.如果∠A=α,∠CEA′=β,
∠BDA′=γ,那么下列式子中正确的是( )
A. γ=2α+β B. γ=α+2β
C. γ=α+β D. γ=180°-α-β
B
A
17.如图,在Rt△ABC中,∠ACB=90°,∠A=52°,
将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=____.
14°
