华东师大版数学七年级下册 9.1.2 三角形的内角和与外角和 课件 (共16张PPT)
文档属性
| 名称 | 华东师大版数学七年级下册 9.1.2 三角形的内角和与外角和 课件 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 648.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
数学 七年级下册 华师版
9.1.2 三角形的内角和与外角和
第9章 多边形
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
2.(2021·仙桃)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,
若∠CDE=160°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
B
D
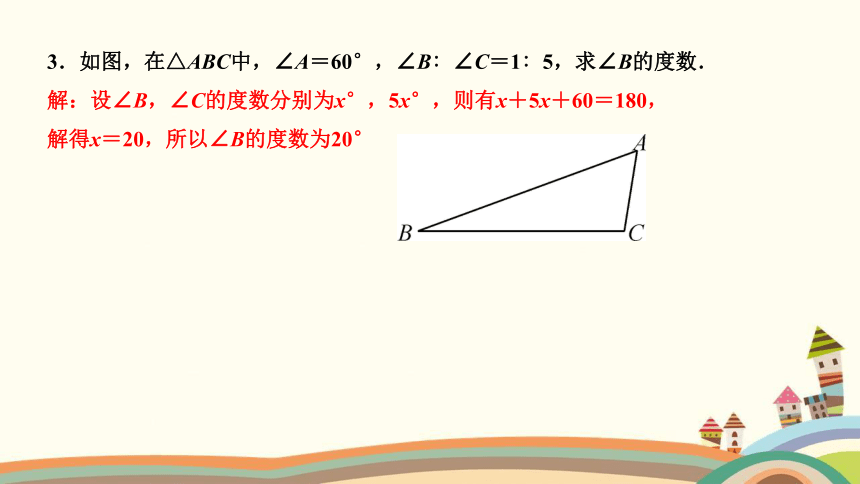
3.如图,在△ABC中,∠A=60°,∠B∶∠C=1∶5,求∠B的度数.
解:设∠B,∠C的度数分别为x°,5x°,则有x+5x+60=180,
解得x=20,所以∠B的度数为20°
4.(南阳九中月考)如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,
若∠BCE=35°,则∠A的度数为( )
A.35° B.45° C.55° D.65°
5.如图,一张直角三角形纸片,剪去直角后,得到一个四边形,
则∠1+∠2=____度.
C
270
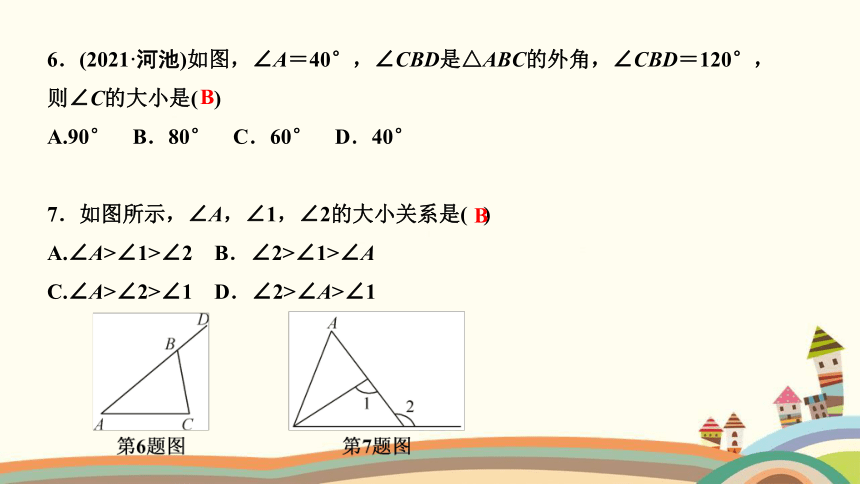
6.(2021·河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,
则∠C的大小是( )
A.90° B.80° C.60° D.40°
7.如图所示,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1
B
B
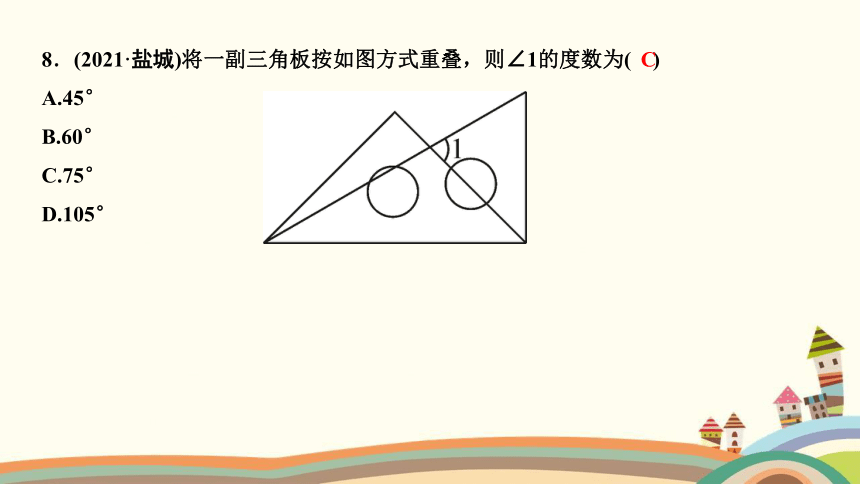
8.(2021·盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
C
9.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=25°,
求∠1的度数.
解:∵∠A+∠C+∠ABC=180°,
∴∠ABC=180°-∠A-∠C=180°-60°-50°=70°,
又∵∠ABC=∠1+∠D,∴∠1=∠ABC-∠D=70°-25°=45°
10.若一个三角形外角的度数之比为2∶3∶4,
则与之对应的三个内角的度数之比为( )
A.4∶3∶2 B.5∶3∶1
C.3∶2∶4 D.3∶1∶5
11.如图,∠1+∠2+∠3+∠4=____度.
B
540
12.(新乡期末)如图,点D在△ABC边AB的延长线上,DE∥BC.
若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
13.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的度数是( )
A.40° B.45° C.50° D.54°
B
A
14.(泰州中考)如图,将分别含有30°,45°角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角的度数为65°,则图中∠α的度数为____.
140°
15.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,
又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,
∴∠DAC=∠BAC-∠1=66°-38°=28°
16.如图,在△ABC中,AD是BC边上的高,AE是角平分线,
∠B=40°,∠DAE=15°,求∠C的度数.
解:∵AD是BC边上的高,∴∠ADE=90°,∠AED+∠DAE=90°,∴∠AED=90°-∠DAE=90°-15°=75°.∵∠B+∠BAE=∠AED,∴∠BAE=∠AED-∠B=75°-40°=35°.∵AE是△ABC的角平分线,∴∠BAC=2∠BAE=2×35°=70°.∵∠B+∠BAC+∠C=180°,∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°
17.如图,在直角三角形ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC边的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC边的延长线于点F,求∠F的度数.
18.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?
解:(1)∠1=∠2.理由如下:∵AD⊥BC,CE⊥AB,∴△ABD和△BCE都是直角三角形,∴∠1+∠B=90°,∠2+∠B=90°,∴∠1=∠2 (2)结论仍然成立.理由如下:∵AD⊥BC,CE⊥AB,∴∠D=∠E=90°,∴∠1+∠4=90°,∠2+∠3=90°.∵∠3=∠4,∴∠1=∠2
数学 七年级下册 华师版
9.1.2 三角形的内角和与外角和
第9章 多边形
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于( )
A.100° B.80° C.60° D.40°
2.(2021·仙桃)如图,在△ABC中,∠C=90°,点D在AC上,DE∥AB,
若∠CDE=160°,则∠B的度数为( )
A.40° B.50° C.60° D.70°
B
D
3.如图,在△ABC中,∠A=60°,∠B∶∠C=1∶5,求∠B的度数.
解:设∠B,∠C的度数分别为x°,5x°,则有x+5x+60=180,
解得x=20,所以∠B的度数为20°
4.(南阳九中月考)如图,在Rt△ABC中,∠ACB=90°,DE过点C且平行于AB,
若∠BCE=35°,则∠A的度数为( )
A.35° B.45° C.55° D.65°
5.如图,一张直角三角形纸片,剪去直角后,得到一个四边形,
则∠1+∠2=____度.
C
270
6.(2021·河池)如图,∠A=40°,∠CBD是△ABC的外角,∠CBD=120°,
则∠C的大小是( )
A.90° B.80° C.60° D.40°
7.如图所示,∠A,∠1,∠2的大小关系是( )
A.∠A>∠1>∠2 B.∠2>∠1>∠A
C.∠A>∠2>∠1 D.∠2>∠A>∠1
B
B
8.(2021·盐城)将一副三角板按如图方式重叠,则∠1的度数为( )
A.45°
B.60°
C.75°
D.105°
C
9.如图,点D,B,C在同一直线上,∠A=60°,∠C=50°,∠D=25°,
求∠1的度数.
解:∵∠A+∠C+∠ABC=180°,
∴∠ABC=180°-∠A-∠C=180°-60°-50°=70°,
又∵∠ABC=∠1+∠D,∴∠1=∠ABC-∠D=70°-25°=45°
10.若一个三角形外角的度数之比为2∶3∶4,
则与之对应的三个内角的度数之比为( )
A.4∶3∶2 B.5∶3∶1
C.3∶2∶4 D.3∶1∶5
11.如图,∠1+∠2+∠3+∠4=____度.
B
540
12.(新乡期末)如图,点D在△ABC边AB的延长线上,DE∥BC.
若∠A=35°,∠C=24°,则∠D的度数是( )
A.24° B.59° C.60° D.69°
13.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于点D,DE∥AB,交AC于点E,则∠ADE的度数是( )
A.40° B.45° C.50° D.54°
B
A
14.(泰州中考)如图,将分别含有30°,45°角的一副三角尺重叠,使直角顶点重合,若两直角重叠形成的角的度数为65°,则图中∠α的度数为____.
140°
15.如图,D是△ABC中的BC边上的一点,且∠1=∠2,∠3=∠4,∠BAC=66°,求∠DAC的度数.
解:设∠1=∠2=x°,∵∠4是△ABD的外角,∴∠4=∠3=∠1+∠2=2x°,
又∵∠BAC+∠3+∠2=180°,∴66°+2x°+x°=180°,∴x°=38°,
∴∠DAC=∠BAC-∠1=66°-38°=28°
16.如图,在△ABC中,AD是BC边上的高,AE是角平分线,
∠B=40°,∠DAE=15°,求∠C的度数.
解:∵AD是BC边上的高,∴∠ADE=90°,∠AED+∠DAE=90°,∴∠AED=90°-∠DAE=90°-15°=75°.∵∠B+∠BAE=∠AED,∴∠BAE=∠AED-∠B=75°-40°=35°.∵AE是△ABC的角平分线,∴∠BAC=2∠BAE=2×35°=70°.∵∠B+∠BAC+∠C=180°,∴∠C=180°-∠B-∠BAC=180°-40°-70°=70°
17.如图,在直角三角形ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE交AC边的延长线于点E.
(1)求∠CBE的度数;
(2)过点D作DF∥BE,交AC边的延长线于点F,求∠F的度数.
18.如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?
解:(1)∠1=∠2.理由如下:∵AD⊥BC,CE⊥AB,∴△ABD和△BCE都是直角三角形,∴∠1+∠B=90°,∠2+∠B=90°,∴∠1=∠2 (2)结论仍然成立.理由如下:∵AD⊥BC,CE⊥AB,∴∠D=∠E=90°,∴∠1+∠4=90°,∠2+∠3=90°.∵∠3=∠4,∴∠1=∠2
