华师大版八年级数学下册试题 17.2 函数的图象 一课一练 (word版 含答案)
文档属性
| 名称 | 华师大版八年级数学下册试题 17.2 函数的图象 一课一练 (word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览

文档简介
17.2 函数的图象 习题 1
第一课时
一、选择题
1.在平面直角坐标系,点P(-1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(m,1)在平面直角坐标系中的第二象限内,则点Q(-m, 0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
3.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下图中的图象中与故事情节相吻合的是( )
二、填空题
4.如下左图的图象中反映的过程是:小明从家跑步到体育馆,在那里锻炼了一阵后又走到新华书店去买书,然后散步回家,其中t表示时间(分钟),s表示小明离家的距离(千米),那么小明在体育馆锻炼和在新华书店买书共用的时间是______分钟.
5.已知点P的坐标为(-1-a2,│a-1│)且a为实数,则点P在平面直角坐标系内的位置为______.
6.若点A(3,m-1)在x轴上,点B(2-n,-2)在y轴上,则点C(3m-1,1-n2)在第_____ 象限.
7.假定甲,乙两人在一次赛跑中,路程s与时间t的关系如上右图所示,我们可以知道:
(1)甲,乙两人中______先到达终点;
(2)乙在这次赛跑中的平均速度为______米/秒.
三、解答题
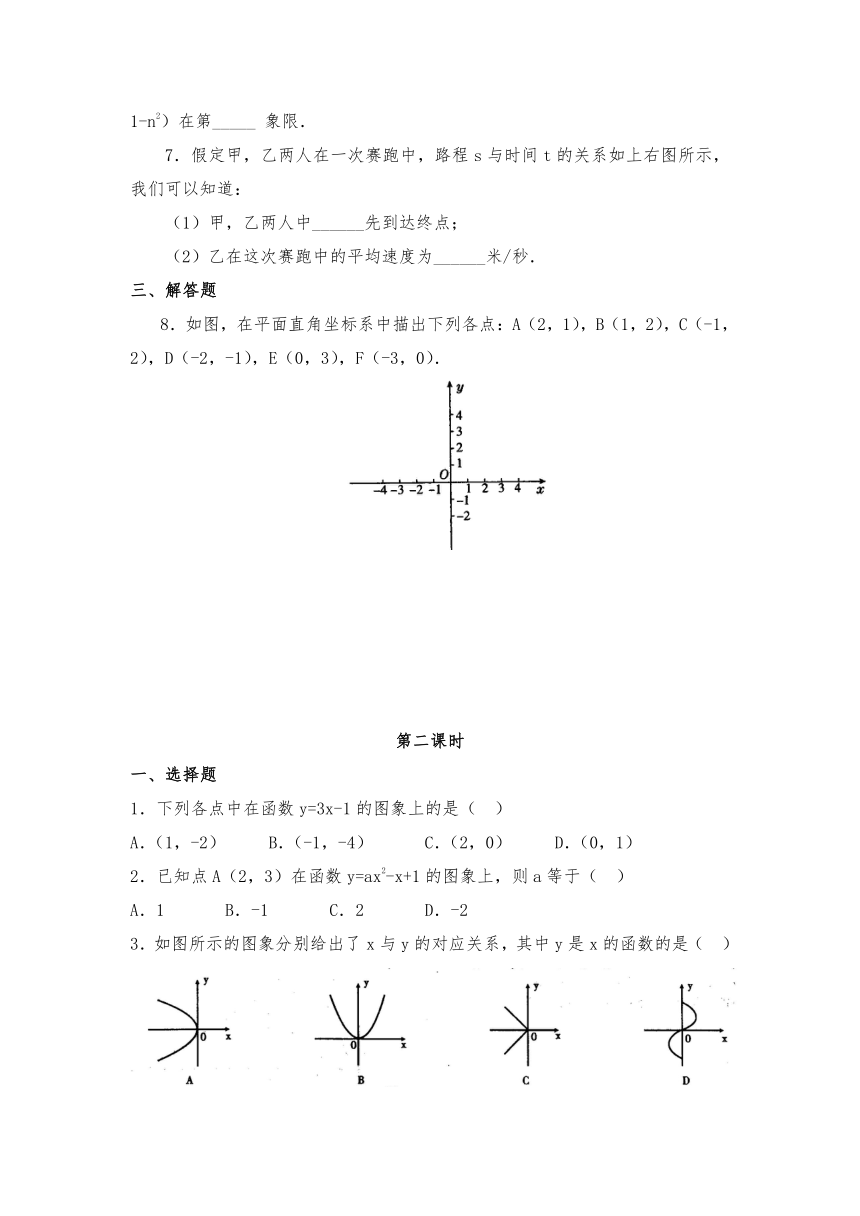
8.如图,在平面直角坐标系中描出下列各点:A(2,1),B(1,2),C(-1,2),D(-2,-1),E(0,3),F(-3,0).
第二课时
一、选择题
1.下列各点中在函数y=3x-1的图象上的是( )
A.(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
2.已知点A(2,3)在函数y=ax2-x+1的图象上,则a等于( )
A.1 B.-1 C.2 D.-2
3.如图所示的图象分别给出了x与y的对应关系,其中y是x的函数的是( )
二、填空题
4.已知函数y=ax2+bx的图象经过M(2,0)和N(1,-6)两点,则a=_________,b=_________.
5.函数y=2x+6与x轴的交点坐标是________,与y轴的交点坐标是________.
6.为了加强公民的节水意识,我市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过的部分按每吨1.8元收费.现有某户居民5月份用水x吨(x>10),应交水费y元,则y关于x的函数关系式是____________.
7.已知A(2,a)是函数y=2x+m与y=mx-2的图象的公共点,则m=_______,a=_______.
三、解答题
8.在同一坐标系内画出下列函数的图象:
(1)y=(x<0) (2)y=-x+1
9.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y的值最大?当x取何值时y的值最小?
(5)当x的值在什么范围内时y随x的增大而增大?当x的值在什么范围内时y随x的增大而减小?
10.某气象中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4km,一段时间内风速保持不变.当沙尘暴遇到绿色植被林时,其风速平均每小时减小1km,最终停止.结合风速与时间的图象,回答下列问题:
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
第一课时参考答案
一、1.B
2.A
3.D
二、4.50
5.第二象限或x轴的负半轴上
6.四
7.(1)甲 (2)8
三、8.解:如图所示.
第二课时参考答案
1.B 2.A 3.B 4.6;-12 5.(-3,0);(0,6)
6.y=1.8(x-10)+12 7.6;10 8.略
9.①-4≤x≤4; ②2,-2,0;
③y=0时x=-3,-1,4;y=4时x=1.5;
④x=1.5时y的值最大,x=-2时y的值最小;
⑤当-2≤x≤1.5时y随x的增大而增大,当-4≤x≤-2和1.5≤x≤4时y随x的增大而减小
10.①风速平均每小时增加2km,经过4h,风速从0变为8km/h;4h后,每小时平均增加4km.持续了6个小时,所以风速达到8+4×6=32km/h.因此从下往上分别填8,32;
②10h至25h期间,风速为32km/h不变,25h后,风速每小时减小1km,变为0要用32h,所以这次沙尘暴共经历了25+32=57(h)
第一课时
一、选择题
1.在平面直角坐标系,点P(-1,m2+1)一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.点P(m,1)在平面直角坐标系中的第二象限内,则点Q(-m, 0)在( )
A.x轴正半轴上 B.x轴负半轴上
C.y轴正半轴上 D.y轴负半轴上
3.“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点……用s1,s2分别表示乌龟和兔子所行的路程,t为时间,则下图中的图象中与故事情节相吻合的是( )
二、填空题
4.如下左图的图象中反映的过程是:小明从家跑步到体育馆,在那里锻炼了一阵后又走到新华书店去买书,然后散步回家,其中t表示时间(分钟),s表示小明离家的距离(千米),那么小明在体育馆锻炼和在新华书店买书共用的时间是______分钟.
5.已知点P的坐标为(-1-a2,│a-1│)且a为实数,则点P在平面直角坐标系内的位置为______.
6.若点A(3,m-1)在x轴上,点B(2-n,-2)在y轴上,则点C(3m-1,1-n2)在第_____ 象限.
7.假定甲,乙两人在一次赛跑中,路程s与时间t的关系如上右图所示,我们可以知道:
(1)甲,乙两人中______先到达终点;
(2)乙在这次赛跑中的平均速度为______米/秒.
三、解答题
8.如图,在平面直角坐标系中描出下列各点:A(2,1),B(1,2),C(-1,2),D(-2,-1),E(0,3),F(-3,0).
第二课时
一、选择题
1.下列各点中在函数y=3x-1的图象上的是( )
A.(1,-2) B.(-1,-4) C.(2,0) D.(0,1)
2.已知点A(2,3)在函数y=ax2-x+1的图象上,则a等于( )
A.1 B.-1 C.2 D.-2
3.如图所示的图象分别给出了x与y的对应关系,其中y是x的函数的是( )
二、填空题
4.已知函数y=ax2+bx的图象经过M(2,0)和N(1,-6)两点,则a=_________,b=_________.
5.函数y=2x+6与x轴的交点坐标是________,与y轴的交点坐标是________.
6.为了加强公民的节水意识,我市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过的部分按每吨1.8元收费.现有某户居民5月份用水x吨(x>10),应交水费y元,则y关于x的函数关系式是____________.
7.已知A(2,a)是函数y=2x+m与y=mx-2的图象的公共点,则m=_______,a=_______.
三、解答题
8.在同一坐标系内画出下列函数的图象:
(1)y=(x<0) (2)y=-x+1
9.已知某一函数的图象如图所示,根据图象回答下列问题:
(1)确定自变量的取值范围;
(2)求当x=-4,-2,4时y的值是多少?
(3)求当y=0,4时x的值是多少?
(4)当x取何值时y的值最大?当x取何值时y的值最小?
(5)当x的值在什么范围内时y随x的增大而增大?当x的值在什么范围内时y随x的增大而减小?
10.某气象中心观测一场沙尘暴从发生到结束的全过程.开始时风速平均每小时增加2km,4h后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4km,一段时间内风速保持不变.当沙尘暴遇到绿色植被林时,其风速平均每小时减小1km,最终停止.结合风速与时间的图象,回答下列问题:
(1)在y轴( )内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
第一课时参考答案
一、1.B
2.A
3.D
二、4.50
5.第二象限或x轴的负半轴上
6.四
7.(1)甲 (2)8
三、8.解:如图所示.
第二课时参考答案
1.B 2.A 3.B 4.6;-12 5.(-3,0);(0,6)
6.y=1.8(x-10)+12 7.6;10 8.略
9.①-4≤x≤4; ②2,-2,0;
③y=0时x=-3,-1,4;y=4时x=1.5;
④x=1.5时y的值最大,x=-2时y的值最小;
⑤当-2≤x≤1.5时y随x的增大而增大,当-4≤x≤-2和1.5≤x≤4时y随x的增大而减小
10.①风速平均每小时增加2km,经过4h,风速从0变为8km/h;4h后,每小时平均增加4km.持续了6个小时,所以风速达到8+4×6=32km/h.因此从下往上分别填8,32;
②10h至25h期间,风速为32km/h不变,25h后,风速每小时减小1km,变为0要用32h,所以这次沙尘暴共经历了25+32=57(h)
