华师大版八年级数学下册试题 17.2 函数的图象 一课一练(word版 含答案)
文档属性
| 名称 | 华师大版八年级数学下册试题 17.2 函数的图象 一课一练(word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 403.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览



文档简介
17.2 函数的图象习题2
第一课时
1.一天,亮亮感冒发烧了,早晨他烧得厉害,吃过药后感冒好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫了.图中能基本反映出亮亮这一天(0~24时)体温的变化情况的是( )
2.某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时装产品150件,未装箱的产品数量为y,生产时间为t,那么y与t的大致图象只能是图中的( )
3.如图,向高为H的圆柱形空水杯里注水,表示注水量y与水深x的关系的图象是( )
4.一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,过了一段时间,汽车到了下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,则图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
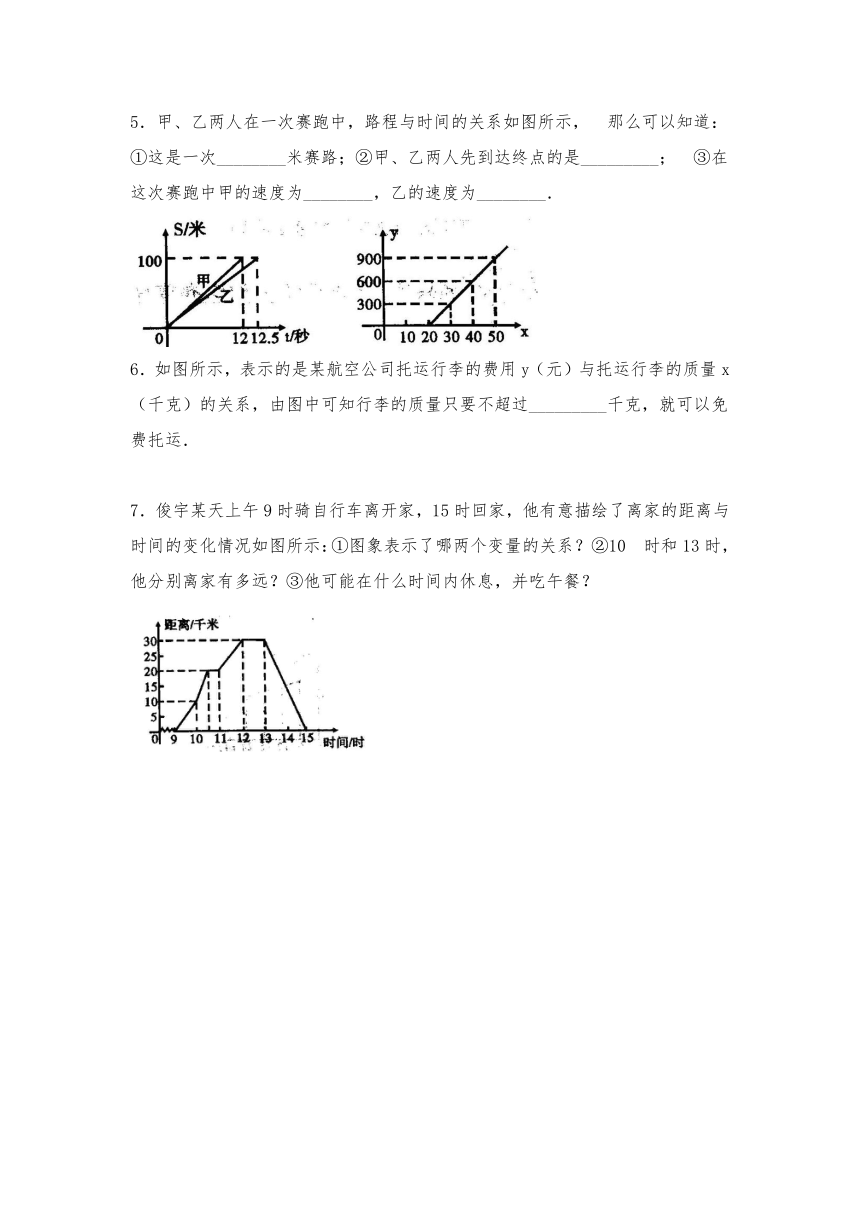
5.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①这是一次________米赛路;②甲、乙两人先到达终点的是_________;③在这次赛跑中甲的速度为________,乙的速度为________.
6.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量只要不超过_________千克,就可以免费托运.
7.俊宇某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况如图所示:①图象表示了哪两个变量的关系?②10时和13时,他分别离家有多远?③他可能在什么时间内休息,并吃午餐?
8.汽车的速度随时间变化的情况如图11-1-11所示:
①这辆汽车的最高时速是多少?
②汽车在行驶了多长时间后停了下来,停了多长时间?
③汽车在第一次匀速行驶时共用了几分钟?速度是多少?在这段时间内,它走了多远?
第二课时
一、训练平台
1.小明的父亲饭后出去散步,从家出发走20min后到一个离家900m的报亭,看了30min报纸后,用15min返回到家里,如图所示,表示小明的父亲离家的时间x与距离y之间关系的是( )
2.一列火车从青岛站出发,加速行驶一段时间后开始匀速行驶,过了一段时间后,火车到达下一个车站,乘客上下车后,火车又加速,一段时间后,再次匀速行驶,如图所示,可以近似地刻画出火车在这段时间内速度变化情况情况的是( )
3.画出函数y=-x+2的图象(在-4与4之间,每隔1取一个x值,列表,并在直角坐标系中描点画图).
二、提高训练
1.如图所示,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过8min漏完,H是沙漏中沙面下降的高度,则H与下落时间t(min)的函数关系用图象表示应该是(如图所示)( )
2.根据水库的剩水量Q(m3)与水泵抽水的时间t(h)之间的函数图象(如图所示),回答下列问题.
(1)水泵抽水前,水库内有_______m3的水,水泵最多能抽水_______h;
(2)水泵抽水8h后,水库的剩水量是_______m3;
(3)当水库的剩水量是1000m3时,水泵已抽水_____h.
3.拖拉机开始工作时,油箱中有油30L,每小时耗油5L.
(1)写出油箱中的余油量Q(L)与工作时间t(h)之间的函数关系式;
(2)求出自变量t的取值范围;
(3)画出函数图象.
三、探索发现
现在已经有不少同学的家中都安装了电话,小华家的电话是按这种方式收费的:月租费24元,30次以内不另收费,超过30次,超过部分每次收0.20元.
(1)试写出小华家一个月内电话费y(元)与电话次数x之间的有关数据,填入下表,并写出其函数关系式;
次数x 10 20 30 40 50 60 70
电话费y/元
(2)这个函数的图象大致是什么形状?和同学交流一下.
四、拓展创新
某地长途汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需购买行李票,行李费费用y(元)是行李质量x(千克)的函数,如图11-11所示.
(1)请写出y与x之间的函数关系式(不要求写自变量的取值范围);
(2)旅客最多可免费携带多少行李?
第一课时答案
1.C 2.A 3.B 4.B 5.①100;②甲;③米/秒;8米/秒
6.20
7.①距离与时间;②10千米,30千米;③12时至13时
8.①这辆汽车的最高时速是120千米/时;
②汽车在行驶了10分钟后停了下来,停了2分钟;
③汽车在第一次匀速行驶时共用了4分钟,速度是90千米/时,在这段时间内,它走了90×=6千米.
第二课时参考答案
一、1.A 2.B
3.解:列表如下:
x -4 -3 -2 -1 0 1 2 3 4
y 3 2 1
描点、连线并画图(如图所示).
二、1.B
2.(1)6000 12 (2)2000 (3)10
3.解:(1)所求的函数关系式是Q=-5t+30.
(2)自变量t的取值范围是0≤t≤6.
(3)①列表如下:
t 0 2 4 6
Q 30 20 10 0
②描点、连线、并画图(如图所示).
三、解:(1)填表为24,24,24,26,28,30,32;
函数解析式为y=
(2)图象如图3所示.
四、(1)y=0.2x-6 (2)30千克
第一课时
1.一天,亮亮感冒发烧了,早晨他烧得厉害,吃过药后感冒好多了,中午时亮亮的体温基本正常,但是下午他的体温又开始上升,直到半夜亮亮才感觉身上不那么发烫了.图中能基本反映出亮亮这一天(0~24时)体温的变化情况的是( )
2.某产品的生产流水线每小时可生产100件产品,生产前没有产品积压,生产3小时后安排工人装箱,若每小时装产品150件,未装箱的产品数量为y,生产时间为t,那么y与t的大致图象只能是图中的( )
3.如图,向高为H的圆柱形空水杯里注水,表示注水量y与水深x的关系的图象是( )
4.一辆公共汽车从车站开出,加速行驶一段后开始匀速行驶,过了一段时间,汽车到了下一个车站,乘客上下车后汽车开始加速,一段时间后又开始匀速行驶,则图中近似地刻画出汽车在这段时间内的速度变化情况的是( )
5.甲、乙两人在一次赛跑中,路程与时间的关系如图所示,那么可以知道:①这是一次________米赛路;②甲、乙两人先到达终点的是_________;③在这次赛跑中甲的速度为________,乙的速度为________.
6.如图所示,表示的是某航空公司托运行李的费用y(元)与托运行李的质量x(千克)的关系,由图中可知行李的质量只要不超过_________千克,就可以免费托运.
7.俊宇某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况如图所示:①图象表示了哪两个变量的关系?②10时和13时,他分别离家有多远?③他可能在什么时间内休息,并吃午餐?
8.汽车的速度随时间变化的情况如图11-1-11所示:
①这辆汽车的最高时速是多少?
②汽车在行驶了多长时间后停了下来,停了多长时间?
③汽车在第一次匀速行驶时共用了几分钟?速度是多少?在这段时间内,它走了多远?
第二课时
一、训练平台
1.小明的父亲饭后出去散步,从家出发走20min后到一个离家900m的报亭,看了30min报纸后,用15min返回到家里,如图所示,表示小明的父亲离家的时间x与距离y之间关系的是( )
2.一列火车从青岛站出发,加速行驶一段时间后开始匀速行驶,过了一段时间后,火车到达下一个车站,乘客上下车后,火车又加速,一段时间后,再次匀速行驶,如图所示,可以近似地刻画出火车在这段时间内速度变化情况情况的是( )
3.画出函数y=-x+2的图象(在-4与4之间,每隔1取一个x值,列表,并在直角坐标系中描点画图).
二、提高训练
1.如图所示,现有一个计时沙漏,开始时盛满沙子,沙子从上部均匀下漏,经过8min漏完,H是沙漏中沙面下降的高度,则H与下落时间t(min)的函数关系用图象表示应该是(如图所示)( )
2.根据水库的剩水量Q(m3)与水泵抽水的时间t(h)之间的函数图象(如图所示),回答下列问题.
(1)水泵抽水前,水库内有_______m3的水,水泵最多能抽水_______h;
(2)水泵抽水8h后,水库的剩水量是_______m3;
(3)当水库的剩水量是1000m3时,水泵已抽水_____h.
3.拖拉机开始工作时,油箱中有油30L,每小时耗油5L.
(1)写出油箱中的余油量Q(L)与工作时间t(h)之间的函数关系式;
(2)求出自变量t的取值范围;
(3)画出函数图象.
三、探索发现
现在已经有不少同学的家中都安装了电话,小华家的电话是按这种方式收费的:月租费24元,30次以内不另收费,超过30次,超过部分每次收0.20元.
(1)试写出小华家一个月内电话费y(元)与电话次数x之间的有关数据,填入下表,并写出其函数关系式;
次数x 10 20 30 40 50 60 70
电话费y/元
(2)这个函数的图象大致是什么形状?和同学交流一下.
四、拓展创新
某地长途汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需购买行李票,行李费费用y(元)是行李质量x(千克)的函数,如图11-11所示.
(1)请写出y与x之间的函数关系式(不要求写自变量的取值范围);
(2)旅客最多可免费携带多少行李?
第一课时答案
1.C 2.A 3.B 4.B 5.①100;②甲;③米/秒;8米/秒
6.20
7.①距离与时间;②10千米,30千米;③12时至13时
8.①这辆汽车的最高时速是120千米/时;
②汽车在行驶了10分钟后停了下来,停了2分钟;
③汽车在第一次匀速行驶时共用了4分钟,速度是90千米/时,在这段时间内,它走了90×=6千米.
第二课时参考答案
一、1.A 2.B
3.解:列表如下:
x -4 -3 -2 -1 0 1 2 3 4
y 3 2 1
描点、连线并画图(如图所示).
二、1.B
2.(1)6000 12 (2)2000 (3)10
3.解:(1)所求的函数关系式是Q=-5t+30.
(2)自变量t的取值范围是0≤t≤6.
(3)①列表如下:
t 0 2 4 6
Q 30 20 10 0
②描点、连线、并画图(如图所示).
三、解:(1)填表为24,24,24,26,28,30,32;
函数解析式为y=
(2)图象如图3所示.
四、(1)y=0.2x-6 (2)30千克
