华师大版八年级数学下册 17.5 实践与探索 一课一练(word版 含答案)
文档属性
| 名称 | 华师大版八年级数学下册 17.5 实践与探索 一课一练(word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览



文档简介
17.5 实践与探索
第一课时
一、选择题
1.如下左图所示,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量为( )
A.小于3吨 B.大于3吨 C.小于4吨 D.大于4吨
2.如上右图所示,OA,OB分别表示甲, 乙两名学生运动路程与时间的一次函数图象,图中s和t分别表示运动路程和时间.根据图象可知,快者的速度比慢者的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
3.若一次函数y=3x-5与y=2x+7图象的交点P的坐标为(12,31),则方程组的解为( )
A. B. C. D.以上答案都不对
二、填空题
4.二元一次方程组的解即为一次函数______和_______的图象交点的坐标.
5.两直线y=2x-1和y=2x+3的位置关系为_________,由此可知方程组的解的情况为_______.
6.某公司市场营销部的营销人员的个人收入与其每月的销售量成一次函数关系,其图象如图 所示, 由图中所给的信息可知, 营销人员没有销售时的收入是________元.
三、解答题
7.利用图象解下列方程组:
(1) (2)
8.作出函数y=x-3的图象,并观察图象回答下列问题:
(1)x取哪些值时,y>0?(2)x取哪些值时,y<0?
四、思考题
9.以下列各组数为坐标的点在一次函数y=2x-1的图象上的有哪几个?为什么?
(1) (2) (3) (4)
第二课时
一、选择题
1.在函数y=x-1的图象上的点是( )
A.(-3,-2) B.(-4,-3)
C.(,) D.(5,)
2.如果一个正比例函数的图象经过点A(3,-1),那么这个正比例函数的解析式为( )
A.y=3x B.y=-3x
C.y=x D.y=-x
3.函数y=3x-6和y=-x+4的图象交于一点,这一点的坐标是( )
A.(-,-) B.(,)
C.(,) D.(-2,3)
4.已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )
A.6 B.10 C.20 D.12
5.直线y=kx+b的图象如图所示,则( )
A.k=-,b=-2 B.k=,b=-2
C.k=-,b=-2 D.k=,b=-2
二、填空题
6.函数y=5x-10,当x=2时,y=______;当x=0时,y=______.
7.函数y=mx-(m-2)的图象经过点(0,3),则m=______.
8.点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是______.
9.当b=______时,直线y=x+b与直线y=2x+3的交点在y轴上.
10.一次函数的图象经过点A(-2,1)和点B(1,-1),它的解析式是______.
三、解答题
11.已知一次函数y=(m-3)x+2m+4的图象过直线y=-x+4与y轴的交点M,求此一次函数的解析式.
12.已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
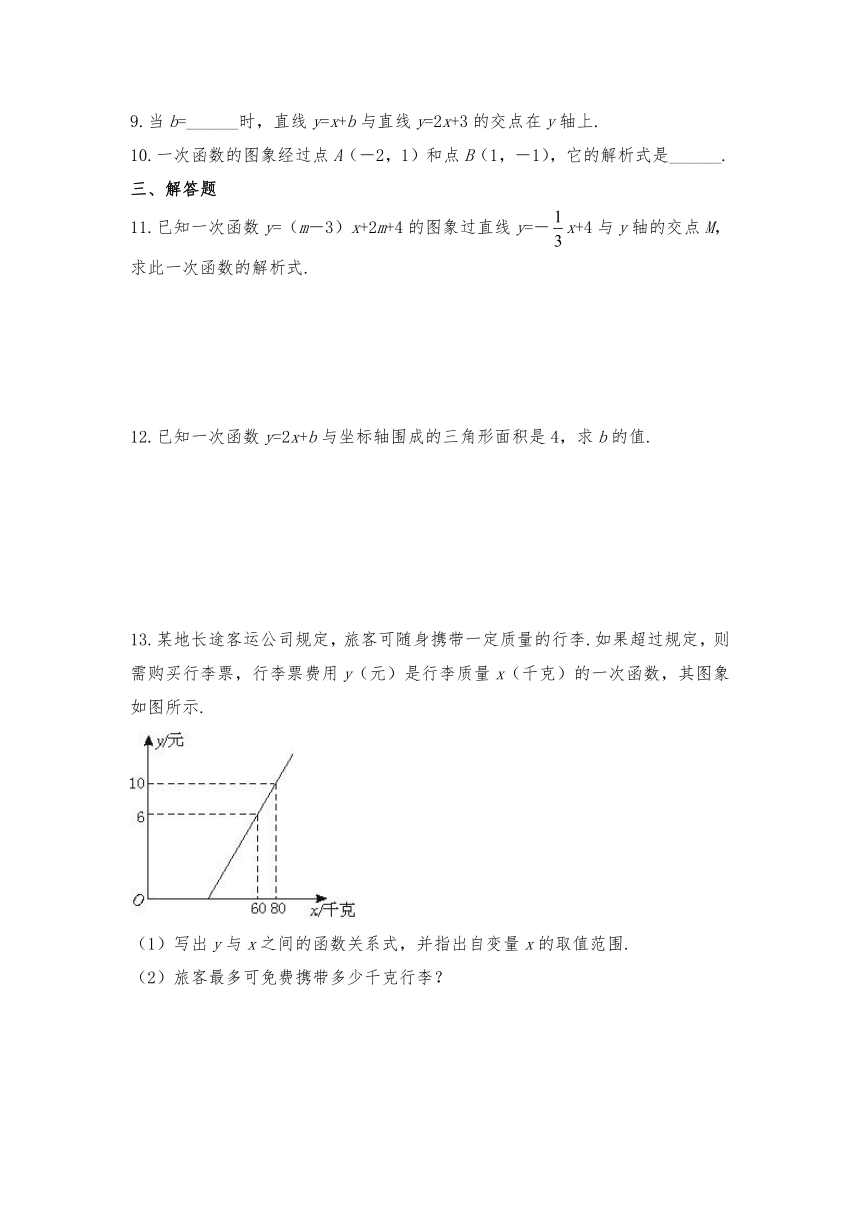
13.某地长途客运公司规定,旅客可随身携带一定质量的行李.如果超过规定,则需购买行李票,行李票费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围.
(2)旅客最多可免费携带多少千克行李?
14.直线y=kx+b过点A(-1,5)且平行于直线y=-x.
(1)求这条直线的解析式.
(2)点B(m,-5)在这条直线上,O为坐标原点,求m的值及△AOB的面积.
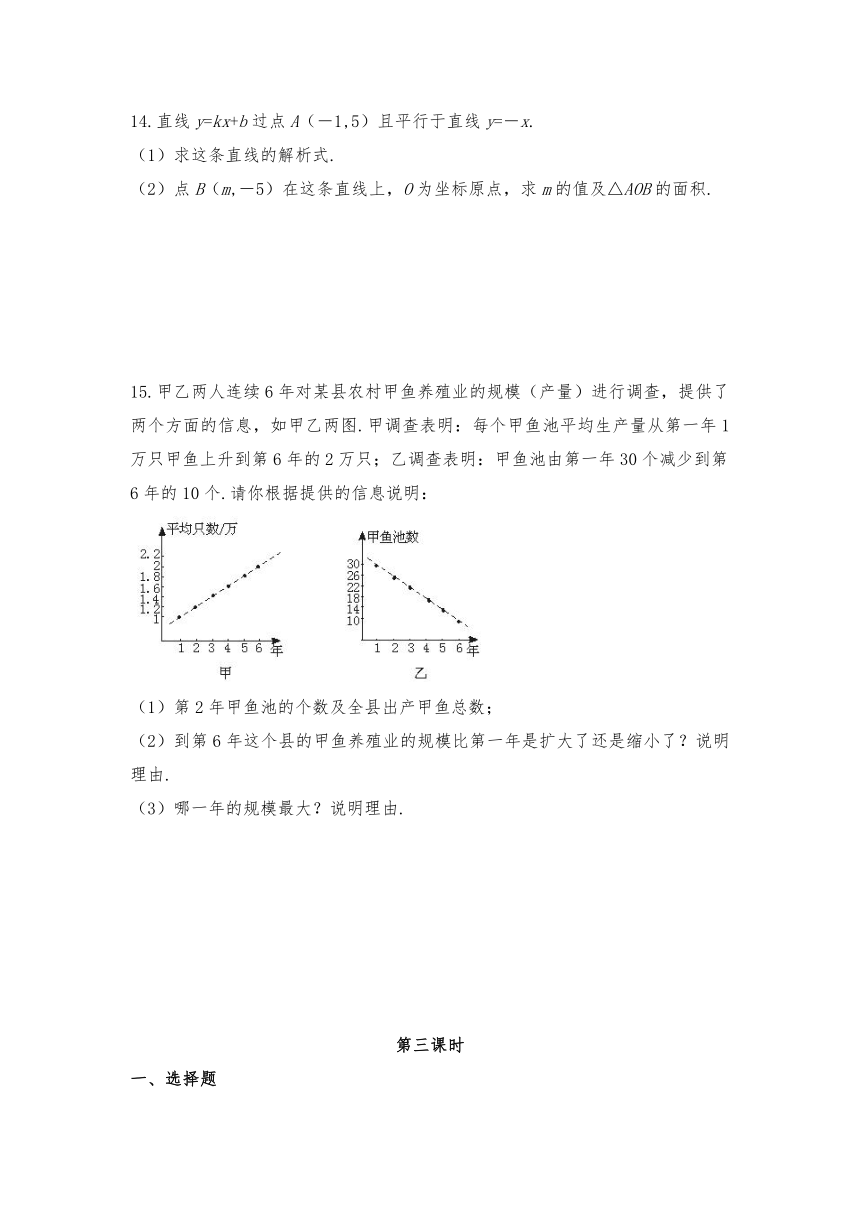
15.甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息,如甲乙两图.甲调查表明:每个甲鱼池平均生产量从第一年1万只甲鱼上升到第6年的2万只;乙调查表明:甲鱼池由第一年30个减少到第6年的10个.请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第一年是扩大了还是缩小了?说明理由.
(3)哪一年的规模最大?说明理由.
第三课时
一、选择题
1.点和都在直线上,则与的关系是( )
A. B. C. D.
2.正比例函数如图所示,则这个函数的解析式为( )
A. B. C. D.
3.直线与直线相交于第三象限,则m的值为( )
A. B. C. D.任意实数
4.在直线上,到x轴或y轴的距离为1的点有( )
A.1个 B.2个 C.3个 D.4个
5.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由此图可知不挂物体时弹簧的长度为( )
A.7cm B.8 cm C.9 cm D.10 cm
二、填空题
1.正比例函数的图像通过点(3,4),那么这个函数的解析式是___________,它的图像在第__________象限,y随x的增大而__________,当时,y=__________,当时,y=__________.
2.如果的图像过原点,那么k=__________.
3.写出的图像上两个点的坐标__________.
4.一次函数的图像与x轴的交点坐标是__________,与y轴的交点坐标是__________.
5.若直线与直线平行,则k=__________.
三、解答题
1.已知直线经过点,且与坐标轴围成的三角形的面积为,求该直线的解析式.
2.直线沿x轴平移后经过点(2,-1),
(1)求平移后直线的解析式;
(2)此时直线沿y轴平移了多少个单位?
3.如图,直线与y轴交于点A,与x轴的正半轴交于点B,等边三角形OCD的顶点C、D分别在线段AB、OB上,且,求k的值.
4.关于x的一次函数的图像与y轴的交点在x轴的上方,且y随x的增大而减小,求a的取值范围.
5.一次函数与的图像相交于x轴上一点,求的值.
6.已知,与x成正比例,与成正比例,并且与时,y的值都是19,求y与x之间的函数关系式.
7.某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水价格x(元)的一次函数.
根据下表提供的数据,求y与x的函数关系式,当水价为每吨10吨时,1吨水生产出的饮料所获的利润是多少?
1吨水的价格x(元) 4 6
用1吨水生产的饮料所获利润y(元) 200 198
第一课时参考答案
一、1.D
2.C
3.A
二、4.y=-2x+4;y=x-4
5.平行;无解
6.300
三、7.解:(1) 由①得y=x-1;由②得y=x-2.如下左图所示, 在同一平面直角坐标系内画出直线y=x-1和y=x-2.由于两直线平行,没有交点,所以原方程组无解.
(2)由7x+4y=2可得y=-x+,由3x-6y=24可得y=x-4.在同一平面直角坐标系内作出一次函数y=-x+的图象L1和y=x-4的图象L2,如上右图所示,观察图象,得L1,L2的交点为(2,-3),所以方程组 的解为.
8.解:函数y=x-3的图象如图所示,由图象知,
(1)当x>3时,y>0;(2)当x<3时,y<0.
四、9.解:满足题意的有(2)(4).理由:(1)因为当x=0时,y=2×0-1=-1≠1, 所以不是二元一次方程y=2x-1的解,点(0,1)不在直线y=2x-1上;(2)当x=1时,y=2x-1=2×1-1=1,所以是二元一次方程y=2x-1的解,点(1,1)在直线y=2x-1上;(3)当x=-1时,y=2×(-1)-1=-2-1=-3≠-2,所以不是二元一次方程y=2x-1的解,点(-1,-2) 不在直线y=2x-1上;(4)当x=5时,y=2×5-1=9,所以是二元一次方程y=2x-1的解,点(5,9)在直线y=2x-1上.
第二课时参考答案
一、1.B 2.D 3.B 4.C 5.B
二、6. 0,-10 7.-1 8.m>n 9. 3 10.y=-x-
三、11.y=-3x+4 12.b=±4
13. (1)y=x-6,x≥30
(2)30
14. (1)y=-x+4
(2)m=9,20
15. (1)26 31.2万只
(2)规模缩小,第一年30万只,第6年20万只
(3)第二年 略
第三课时参考答案
一、选择题
1. D 2. B 3. C 4. C 5. D
二、填空题
1. ,一、三,增大,,
2.
3. (0,0),
4.,
5.
三、解答题
1.或.
2.(1)
(2)设y轴向下平移8个单位,得到.
3.设 ∴ ,由B、C在直线上,可得.
4. ∴
5.由可得,由,可得,而,
∴
6.设, ∴ ,
∴ 解得 ∴.
7.设,
则 解得
∴ 一次函数解析式为,当时,,即当水价为每吨10元时,1吨水生产饮料获得的利润是194元.
第一课时
一、选择题
1.如下左图所示,l1反映了某公司的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,当该公司赢利(收入大于成本)时,销售量为( )
A.小于3吨 B.大于3吨 C.小于4吨 D.大于4吨
2.如上右图所示,OA,OB分别表示甲, 乙两名学生运动路程与时间的一次函数图象,图中s和t分别表示运动路程和时间.根据图象可知,快者的速度比慢者的速度每秒快( )
A.2.5米 B.2米 C.1.5米 D.1米
3.若一次函数y=3x-5与y=2x+7图象的交点P的坐标为(12,31),则方程组的解为( )
A. B. C. D.以上答案都不对
二、填空题
4.二元一次方程组的解即为一次函数______和_______的图象交点的坐标.
5.两直线y=2x-1和y=2x+3的位置关系为_________,由此可知方程组的解的情况为_______.
6.某公司市场营销部的营销人员的个人收入与其每月的销售量成一次函数关系,其图象如图 所示, 由图中所给的信息可知, 营销人员没有销售时的收入是________元.
三、解答题
7.利用图象解下列方程组:
(1) (2)
8.作出函数y=x-3的图象,并观察图象回答下列问题:
(1)x取哪些值时,y>0?(2)x取哪些值时,y<0?
四、思考题
9.以下列各组数为坐标的点在一次函数y=2x-1的图象上的有哪几个?为什么?
(1) (2) (3) (4)
第二课时
一、选择题
1.在函数y=x-1的图象上的点是( )
A.(-3,-2) B.(-4,-3)
C.(,) D.(5,)
2.如果一个正比例函数的图象经过点A(3,-1),那么这个正比例函数的解析式为( )
A.y=3x B.y=-3x
C.y=x D.y=-x
3.函数y=3x-6和y=-x+4的图象交于一点,这一点的坐标是( )
A.(-,-) B.(,)
C.(,) D.(-2,3)
4.已知直线y=-x+6和y=x-2,则它们与y轴所围成的三角形的面积为( )
A.6 B.10 C.20 D.12
5.直线y=kx+b的图象如图所示,则( )
A.k=-,b=-2 B.k=,b=-2
C.k=-,b=-2 D.k=,b=-2
二、填空题
6.函数y=5x-10,当x=2时,y=______;当x=0时,y=______.
7.函数y=mx-(m-2)的图象经过点(0,3),则m=______.
8.点(1,m),(2,n)在函数y=-x+1的图象上,则m、n的大小关系是______.
9.当b=______时,直线y=x+b与直线y=2x+3的交点在y轴上.
10.一次函数的图象经过点A(-2,1)和点B(1,-1),它的解析式是______.
三、解答题
11.已知一次函数y=(m-3)x+2m+4的图象过直线y=-x+4与y轴的交点M,求此一次函数的解析式.
12.已知一次函数y=2x+b与坐标轴围成的三角形面积是4,求b的值.
13.某地长途客运公司规定,旅客可随身携带一定质量的行李.如果超过规定,则需购买行李票,行李票费用y(元)是行李质量x(千克)的一次函数,其图象如图所示.
(1)写出y与x之间的函数关系式,并指出自变量x的取值范围.
(2)旅客最多可免费携带多少千克行李?
14.直线y=kx+b过点A(-1,5)且平行于直线y=-x.
(1)求这条直线的解析式.
(2)点B(m,-5)在这条直线上,O为坐标原点,求m的值及△AOB的面积.
15.甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息,如甲乙两图.甲调查表明:每个甲鱼池平均生产量从第一年1万只甲鱼上升到第6年的2万只;乙调查表明:甲鱼池由第一年30个减少到第6年的10个.请你根据提供的信息说明:
(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第一年是扩大了还是缩小了?说明理由.
(3)哪一年的规模最大?说明理由.
第三课时
一、选择题
1.点和都在直线上,则与的关系是( )
A. B. C. D.
2.正比例函数如图所示,则这个函数的解析式为( )
A. B. C. D.
3.直线与直线相交于第三象限,则m的值为( )
A. B. C. D.任意实数
4.在直线上,到x轴或y轴的距离为1的点有( )
A.1个 B.2个 C.3个 D.4个
5.弹簧的长度与所挂物体的质量的关系为一次函数,如图所示,由此图可知不挂物体时弹簧的长度为( )
A.7cm B.8 cm C.9 cm D.10 cm
二、填空题
1.正比例函数的图像通过点(3,4),那么这个函数的解析式是___________,它的图像在第__________象限,y随x的增大而__________,当时,y=__________,当时,y=__________.
2.如果的图像过原点,那么k=__________.
3.写出的图像上两个点的坐标__________.
4.一次函数的图像与x轴的交点坐标是__________,与y轴的交点坐标是__________.
5.若直线与直线平行,则k=__________.
三、解答题
1.已知直线经过点,且与坐标轴围成的三角形的面积为,求该直线的解析式.
2.直线沿x轴平移后经过点(2,-1),
(1)求平移后直线的解析式;
(2)此时直线沿y轴平移了多少个单位?
3.如图,直线与y轴交于点A,与x轴的正半轴交于点B,等边三角形OCD的顶点C、D分别在线段AB、OB上,且,求k的值.
4.关于x的一次函数的图像与y轴的交点在x轴的上方,且y随x的增大而减小,求a的取值范围.
5.一次函数与的图像相交于x轴上一点,求的值.
6.已知,与x成正比例,与成正比例,并且与时,y的值都是19,求y与x之间的函数关系式.
7.某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水价格x(元)的一次函数.
根据下表提供的数据,求y与x的函数关系式,当水价为每吨10吨时,1吨水生产出的饮料所获的利润是多少?
1吨水的价格x(元) 4 6
用1吨水生产的饮料所获利润y(元) 200 198
第一课时参考答案
一、1.D
2.C
3.A
二、4.y=-2x+4;y=x-4
5.平行;无解
6.300
三、7.解:(1) 由①得y=x-1;由②得y=x-2.如下左图所示, 在同一平面直角坐标系内画出直线y=x-1和y=x-2.由于两直线平行,没有交点,所以原方程组无解.
(2)由7x+4y=2可得y=-x+,由3x-6y=24可得y=x-4.在同一平面直角坐标系内作出一次函数y=-x+的图象L1和y=x-4的图象L2,如上右图所示,观察图象,得L1,L2的交点为(2,-3),所以方程组 的解为.
8.解:函数y=x-3的图象如图所示,由图象知,
(1)当x>3时,y>0;(2)当x<3时,y<0.
四、9.解:满足题意的有(2)(4).理由:(1)因为当x=0时,y=2×0-1=-1≠1, 所以不是二元一次方程y=2x-1的解,点(0,1)不在直线y=2x-1上;(2)当x=1时,y=2x-1=2×1-1=1,所以是二元一次方程y=2x-1的解,点(1,1)在直线y=2x-1上;(3)当x=-1时,y=2×(-1)-1=-2-1=-3≠-2,所以不是二元一次方程y=2x-1的解,点(-1,-2) 不在直线y=2x-1上;(4)当x=5时,y=2×5-1=9,所以是二元一次方程y=2x-1的解,点(5,9)在直线y=2x-1上.
第二课时参考答案
一、1.B 2.D 3.B 4.C 5.B
二、6. 0,-10 7.-1 8.m>n 9. 3 10.y=-x-
三、11.y=-3x+4 12.b=±4
13. (1)y=x-6,x≥30
(2)30
14. (1)y=-x+4
(2)m=9,20
15. (1)26 31.2万只
(2)规模缩小,第一年30万只,第6年20万只
(3)第二年 略
第三课时参考答案
一、选择题
1. D 2. B 3. C 4. C 5. D
二、填空题
1. ,一、三,增大,,
2.
3. (0,0),
4.,
5.
三、解答题
1.或.
2.(1)
(2)设y轴向下平移8个单位,得到.
3.设 ∴ ,由B、C在直线上,可得.
4. ∴
5.由可得,由,可得,而,
∴
6.设, ∴ ,
∴ 解得 ∴.
7.设,
则 解得
∴ 一次函数解析式为,当时,,即当水价为每吨10元时,1吨水生产饮料获得的利润是194元.
