华师大版八年级数学下册 18.2 平行四边形的判定 一课一练(word版 含答案)
文档属性
| 名称 | 华师大版八年级数学下册 18.2 平行四边形的判定 一课一练(word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 14:54:44 | ||
图片预览




文档简介
18.2《平行四边形的判定》习题2
第一课时
1.下面几组条件中,能判定一个四边形是平行四边形的( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
2.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,在中,,是上的点,∥交于点,∥交于点,那么四边形的周长是( )
A.5 B.10 C.15 D.20
4.□的周长是36cm,=8 cm,则= cm.
5.在四边形中,已知∥,要使四边形为平行四边形,需要增加的条件是 (填一个你认为正确的条件).
6.已知:如图,、是□的对角线上的两点,且.
求证:四边形是平行四边形.
7.如图,平行四边形中,试用三种方法将平行四边形分成面积相等的四部分.(要求用文字简述你所设计的三种方法,并在所给的三个平行四边形中正确画图)
8.如图,李村有一口呈四边形的池塘,在它的四个角、、、处均有一棵桃树,现在村委会准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持桃树不动,并要求扩建后的池塘呈平行四边形形状,请问该村能否实现这一设想?若能,请设计并画出图形,简单描述你的画法;若不能,请说明理由.
第二课时
一、选择题
1.四边形ABCD,从(1)AB∥CD;(2)AB=CD;(3)BC∥AD;(4)BC=AD这四个条件中任选两个,其中能使四边形ABCD是平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
2.四边形的四条边长分别是a,b,c,d,其中a,b为一组对边边长,c,d 为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
3.下列说法正确的是( )
A.若一个四边形的一条对角线平分另一条对角线,则这个四边形是平行四边形
B.对角线互相平分的四边形一定是平行四边形
C.一组对边相等的四边形是平行四边形
D.有两个角相等的四边形是平行四边形
二、填空题
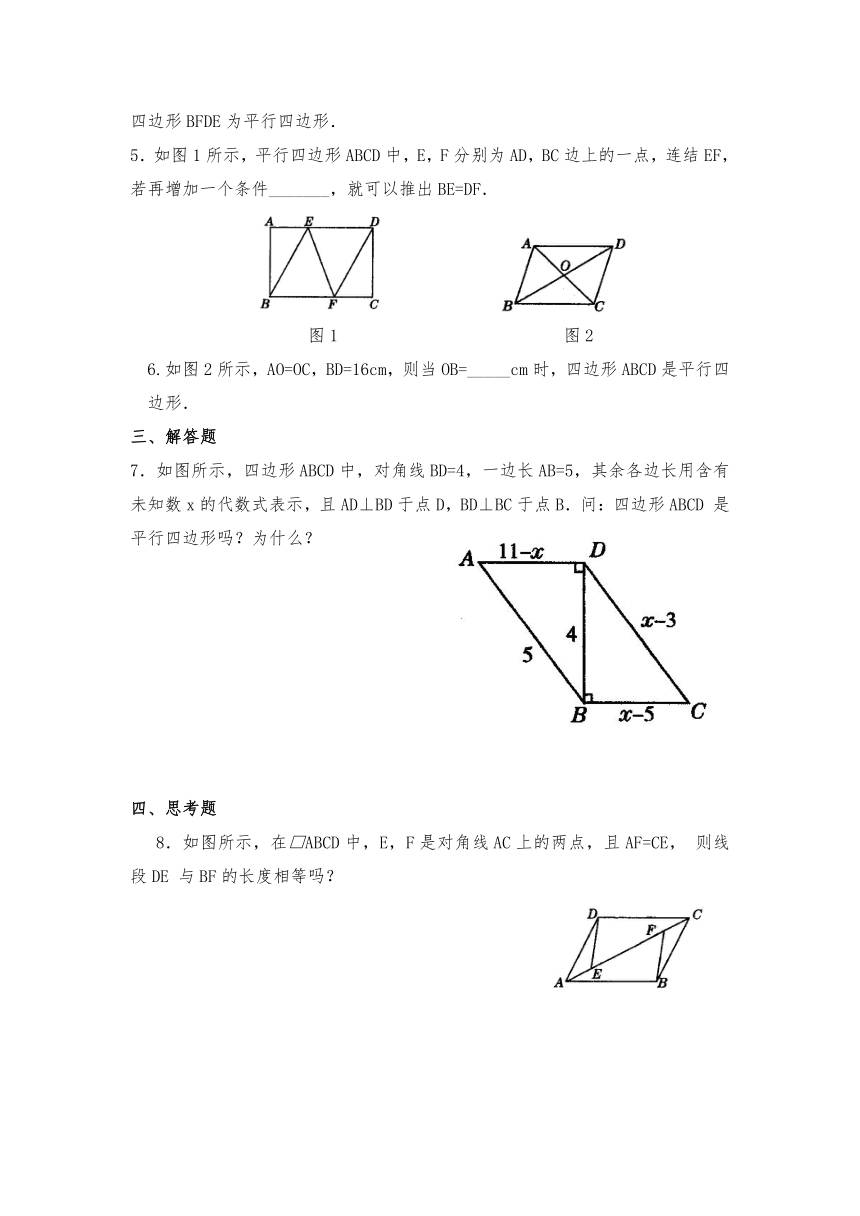
4.在□ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动,点F从C 向B运动,点E的速度m与点F的速度n满足_______关系时,四边形BFDE为平行四边形.
5.如图1所示,平行四边形ABCD中,E,F分别为AD,BC边上的一点,连结EF,若再增加一个条件_______,就可以推出BE=DF.
图1 图2
6.如图2所示,AO=OC,BD=16cm,则当OB=_____cm时,四边形ABCD是平行四边形.
三、解答题
7.如图所示,四边形ABCD中,对角线BD=4,一边长AB=5,其余各边长用含有未知数x的代数式表示,且AD⊥BD于点D,BD⊥BC于点B.问:四边形ABCD 是平行四边形吗?为什么?
四、思考题
8.如图所示,在□ABCD中,E,F是对角线AC上的两点,且AF=CE, 则线段DE 与BF的长度相等吗?
第三课时
一、填空题
1.如图,□ABCD中,CE=DF,则四边形ABEF是____________.
1题图
2.如图,□ABCD,EF∥AB,GH∥AD,MN∥AD,图中共有______个平行四边形.
2题图
3.已知三条线段长分别为10,14,20,以其中两条为对角线,其余一条为边可以画出______个平行四边形.
4.已知三条线段长分别为7,15,20,以其中一条为对角线,另两条为邻边,可以画出______个平行四边形.
5.已知:如图,四边形AEFD和EBCF都是平行四边形,则四边形ABCD是______.
5题图
二、选择题
6.能判定一个四边形是平行四边形的条件是( ).
(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补
(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补
7.能判定四边形ABCD是平行四边形的题设是( ).
(A)AD=BC,AB∥CD (B)∠A=∠B,∠C=∠D
(C)AB=BC,AD=DC (D)AB∥CD,CD=AB
8.能判定四边形ABCD是平行四边形的条件是:∠A∶∠B∶∠C∶∠D的值为( ).
(A)1∶2∶3∶4 (B)1∶4∶2∶3
(C)1∶2∶2∶1 (D)1∶2∶1∶2
9.如图,E、F分别是□ABCD的边AB、CD的中点,则图中平行四边形的个数共有( ).
(A)2个 (B)3个
(C)4个 (D)5个
10.□ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).
(A)(1,-2) (B)(2,-1) (C)(1,-3) (D)(2,-3)
11.如图,□ABCD中,对角线AC、BD交于点O,将△AOD平移至△BEC的位置,则图中与OA相等的其他线段有( ).
(A)1条 (B)2条
(C)3条 (D)4条
三、解答题
12.已知:如图,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可).
(1)连结______;
(2)猜想:______=______;
(3)证明:
13.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件______.(只添加一个条件)
证明:
14.已知:如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
15.已知:如图,在等边△ABC中,D、F分别为CB、BA上的点,且CD=BF,以AD为边作等边三角形ADE.
求证:(1)△ACD≌△CBF;
(2)四边形CDEF为平行四边形.
16.若一次函数y=2x-1和反比例函数的图象都经过点(1,1).
(1)求反比例函数的解析式;
(2)已知点A在第三象限,且同时在两个函数的图象上,利用图象求点A的坐标;
(3)利用(2)的结果,若点B的坐标为(2,0),且以点A、O、B、P为顶点的四边形是平行四边形,请你直接写出点P的坐标.
17.如图,点A(m,m+1),B(m+3,m-1)在反比例函数的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
第一课时参考答案
1.B, 2.C ,3. B, 4.10,5. ∥(或)
6.提示:连结AC,证明四边形的对角线互相平分.
7.分法如下:
8.提示:能.如图, □EFGH即为所求,其中EF∥DB∥HG,EH∥FG∥AC
第二课时答案
一、1.B
2.B
3.B
二、4.相等 5.AE=CF 6.8
三、7.解:如图所示,四边形ABCD是平行四边形.理由如下:
在Rt △BCD中,根据勾股定理,得BC2+BD2=DC2,
即(x-5)2+42=(x-3)2,解得x=8.
所以AD=11-8=3,BC=x-5=3,DC=x-3=8-3=5,
所以AD=BC,AB=DC.所以四边形ABCD是平行四边形.
四、8.解:线段DE与BF的长度相等;连结BD交AC于O点,连结DF,BE,
如图所示.在ABCD中,DO=OB,AO=OC,又因为AF=EC,
所以AF-AO=CE-OC,即OF=OE,所以四边形DEBF是平行四边形,所以DE=BF.
第三课时参考答案
1.平行四边形. 2.18. 3.2. 4.3. 5.平行四边形.
6.C. 7.D. 8.D. 9.C. 10.A. 11.B.
12.(1)BF(或DF); (2)BF=DE(或BE=DF);
(3)提示:连结DF(或BF),证四边形DEBF是平行四边形.
13.提示:D是BC的中点.
14.DE+DF=10
15.提示:(1)∵△ABC为等边三角形,∴AC=CB,∠ACD=∠CBF=60°.
又∵CD=BF,∴△ACD≌△CBF.
(2)∵△ACD≌△CBF,∴AD=CF,∠CAD=∠BCF.
∵△AED为等边三角形,∴∠ADE=60°,且AD=DE.∴FC=DE.
∵∠EDB+60°=∠BDA=∠CAD+∠ACD=∠BCF+60°,
∴∠EDB=∠BCF.∴ED∥FC.
∵EDFC,∴四边形CDEF为平行四边形.
16.(1);(2); (3)P1(-1.5,-2),P2(-2.5,-2)或P3
(2.5,2).
17.(1)m=3,k=12;
(2)或
第一课时
1.下面几组条件中,能判定一个四边形是平行四边形的( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
2.已知A、B、C三点不在同一条直线上,则以这三点为顶点的平行四边形共有 ( )
A.1个 B.2个 C.3个 D.4个
3.如图,在中,,是上的点,∥交于点,∥交于点,那么四边形的周长是( )
A.5 B.10 C.15 D.20
4.□的周长是36cm,=8 cm,则= cm.
5.在四边形中,已知∥,要使四边形为平行四边形,需要增加的条件是 (填一个你认为正确的条件).
6.已知:如图,、是□的对角线上的两点,且.
求证:四边形是平行四边形.
7.如图,平行四边形中,试用三种方法将平行四边形分成面积相等的四部分.(要求用文字简述你所设计的三种方法,并在所给的三个平行四边形中正确画图)
8.如图,李村有一口呈四边形的池塘,在它的四个角、、、处均有一棵桃树,现在村委会准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持桃树不动,并要求扩建后的池塘呈平行四边形形状,请问该村能否实现这一设想?若能,请设计并画出图形,简单描述你的画法;若不能,请说明理由.
第二课时
一、选择题
1.四边形ABCD,从(1)AB∥CD;(2)AB=CD;(3)BC∥AD;(4)BC=AD这四个条件中任选两个,其中能使四边形ABCD是平行四边形的选法有( )
A.3种 B.4种 C.5种 D.6种
2.四边形的四条边长分别是a,b,c,d,其中a,b为一组对边边长,c,d 为另一组对边边长且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
A.任意四边形 B.平行四边形
C.对角线相等的四边形 D.对角线垂直的四边形
3.下列说法正确的是( )
A.若一个四边形的一条对角线平分另一条对角线,则这个四边形是平行四边形
B.对角线互相平分的四边形一定是平行四边形
C.一组对边相等的四边形是平行四边形
D.有两个角相等的四边形是平行四边形
二、填空题
4.在□ABCD中,点E,F分别是线段AD,BC上的两动点,点E从点A向D运动,点F从C 向B运动,点E的速度m与点F的速度n满足_______关系时,四边形BFDE为平行四边形.
5.如图1所示,平行四边形ABCD中,E,F分别为AD,BC边上的一点,连结EF,若再增加一个条件_______,就可以推出BE=DF.
图1 图2
6.如图2所示,AO=OC,BD=16cm,则当OB=_____cm时,四边形ABCD是平行四边形.
三、解答题
7.如图所示,四边形ABCD中,对角线BD=4,一边长AB=5,其余各边长用含有未知数x的代数式表示,且AD⊥BD于点D,BD⊥BC于点B.问:四边形ABCD 是平行四边形吗?为什么?
四、思考题
8.如图所示,在□ABCD中,E,F是对角线AC上的两点,且AF=CE, 则线段DE 与BF的长度相等吗?
第三课时
一、填空题
1.如图,□ABCD中,CE=DF,则四边形ABEF是____________.
1题图
2.如图,□ABCD,EF∥AB,GH∥AD,MN∥AD,图中共有______个平行四边形.
2题图
3.已知三条线段长分别为10,14,20,以其中两条为对角线,其余一条为边可以画出______个平行四边形.
4.已知三条线段长分别为7,15,20,以其中一条为对角线,另两条为邻边,可以画出______个平行四边形.
5.已知:如图,四边形AEFD和EBCF都是平行四边形,则四边形ABCD是______.
5题图
二、选择题
6.能判定一个四边形是平行四边形的条件是( ).
(A)一组对边平行,另一组对边相等 (B)一组对边平行,一组对角互补
(C)一组对角相等,一组邻角互补 (D)一组对角相等,另一组对角互补
7.能判定四边形ABCD是平行四边形的题设是( ).
(A)AD=BC,AB∥CD (B)∠A=∠B,∠C=∠D
(C)AB=BC,AD=DC (D)AB∥CD,CD=AB
8.能判定四边形ABCD是平行四边形的条件是:∠A∶∠B∶∠C∶∠D的值为( ).
(A)1∶2∶3∶4 (B)1∶4∶2∶3
(C)1∶2∶2∶1 (D)1∶2∶1∶2
9.如图,E、F分别是□ABCD的边AB、CD的中点,则图中平行四边形的个数共有( ).
(A)2个 (B)3个
(C)4个 (D)5个
10.□ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为( ).
(A)(1,-2) (B)(2,-1) (C)(1,-3) (D)(2,-3)
11.如图,□ABCD中,对角线AC、BD交于点O,将△AOD平移至△BEC的位置,则图中与OA相等的其他线段有( ).
(A)1条 (B)2条
(C)3条 (D)4条
三、解答题
12.已知:如图,在□ABCD中,点E、F在对角线AC上,且AE=CF.请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可).
(1)连结______;
(2)猜想:______=______;
(3)证明:
13.如图,在△ABC中,EF为△ABC的中位线,D为BC边上一点(不与B、C重合),AD与EF交于点O,连结EF、DF,要使四边形AEDF为平行四边形,需要添加条件______.(只添加一个条件)
证明:
14.已知:如图,△ABC中,AB=AC=10,D是BC边上的任意一点,分别作DF∥AB交AC于F,DE∥AC交AB于E,求DE+DF的值.
15.已知:如图,在等边△ABC中,D、F分别为CB、BA上的点,且CD=BF,以AD为边作等边三角形ADE.
求证:(1)△ACD≌△CBF;
(2)四边形CDEF为平行四边形.
16.若一次函数y=2x-1和反比例函数的图象都经过点(1,1).
(1)求反比例函数的解析式;
(2)已知点A在第三象限,且同时在两个函数的图象上,利用图象求点A的坐标;
(3)利用(2)的结果,若点B的坐标为(2,0),且以点A、O、B、P为顶点的四边形是平行四边形,请你直接写出点P的坐标.
17.如图,点A(m,m+1),B(m+3,m-1)在反比例函数的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,以点A,B,M,N为顶点的四边形是平行四边形,试求直线MN的函数表达式.
第一课时参考答案
1.B, 2.C ,3. B, 4.10,5. ∥(或)
6.提示:连结AC,证明四边形的对角线互相平分.
7.分法如下:
8.提示:能.如图, □EFGH即为所求,其中EF∥DB∥HG,EH∥FG∥AC
第二课时答案
一、1.B
2.B
3.B
二、4.相等 5.AE=CF 6.8
三、7.解:如图所示,四边形ABCD是平行四边形.理由如下:
在Rt △BCD中,根据勾股定理,得BC2+BD2=DC2,
即(x-5)2+42=(x-3)2,解得x=8.
所以AD=11-8=3,BC=x-5=3,DC=x-3=8-3=5,
所以AD=BC,AB=DC.所以四边形ABCD是平行四边形.
四、8.解:线段DE与BF的长度相等;连结BD交AC于O点,连结DF,BE,
如图所示.在ABCD中,DO=OB,AO=OC,又因为AF=EC,
所以AF-AO=CE-OC,即OF=OE,所以四边形DEBF是平行四边形,所以DE=BF.
第三课时参考答案
1.平行四边形. 2.18. 3.2. 4.3. 5.平行四边形.
6.C. 7.D. 8.D. 9.C. 10.A. 11.B.
12.(1)BF(或DF); (2)BF=DE(或BE=DF);
(3)提示:连结DF(或BF),证四边形DEBF是平行四边形.
13.提示:D是BC的中点.
14.DE+DF=10
15.提示:(1)∵△ABC为等边三角形,∴AC=CB,∠ACD=∠CBF=60°.
又∵CD=BF,∴△ACD≌△CBF.
(2)∵△ACD≌△CBF,∴AD=CF,∠CAD=∠BCF.
∵△AED为等边三角形,∴∠ADE=60°,且AD=DE.∴FC=DE.
∵∠EDB+60°=∠BDA=∠CAD+∠ACD=∠BCF+60°,
∴∠EDB=∠BCF.∴ED∥FC.
∵EDFC,∴四边形CDEF为平行四边形.
16.(1);(2); (3)P1(-1.5,-2),P2(-2.5,-2)或P3
(2.5,2).
17.(1)m=3,k=12;
(2)或
