苏科版七上数学第二章有理数(复习)
图片预览



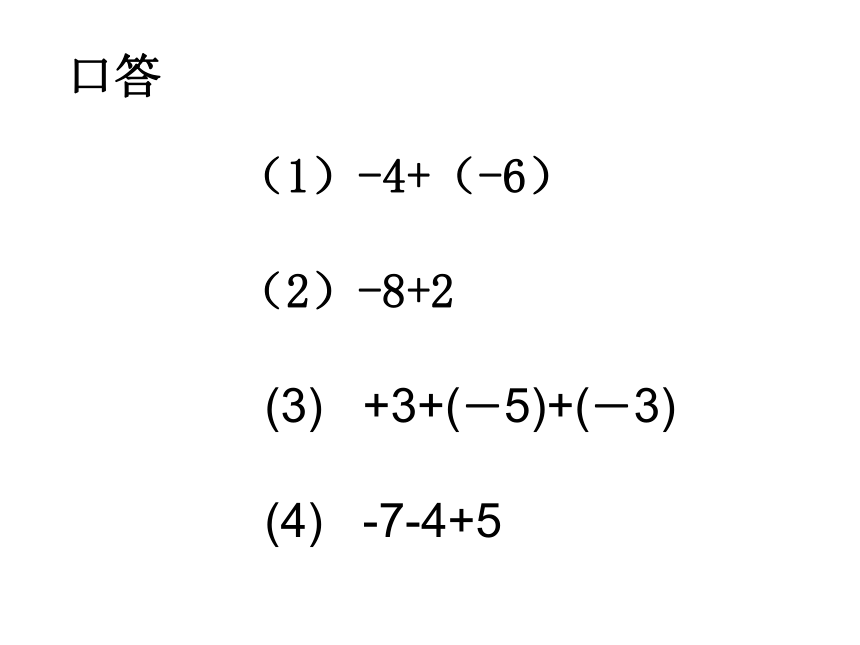




文档简介
课件45张PPT。§2有理数1、有理数的分类分数整数2、数轴·原点····210-1-23、绝对值·····210-1-2 数轴上表示一个数的点到原点的距离叫做绝对值绝对值最小的数是什么?4、符号不同而绝对值相等的
两个数叫做互为相反数 若xy互为相反数,
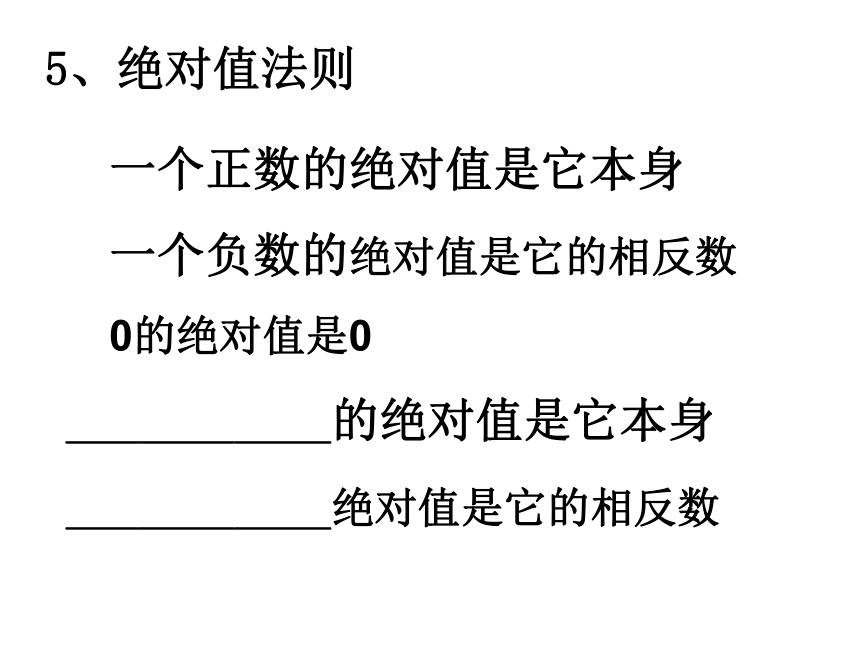
则x+y=0一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0___________的绝对值是它本身
___________绝对值是它的相反数5、绝对值法则6、有理数加法法则
(1)同号两数相加,取原来的符号
并把绝对值相加;
(2)异号两数相加,取绝对值较大
的数的符号,并用较大的绝对值
减去较小的绝对值。
(3) 0加一个数还得这个数7、有理数减法法则
减去一个数等于加上这个数的相反数即:a-b=a+(-b)口答(1)-4+(-6)
(2)-8+2
(3) +3+(-5)+(-3)
(4) -7-4+58、有理数乘法法则
两数相乘,
同号得“+”,
异号得“-”
并把绝对值相乘。口 答(1). -2×(+3)
(2).(-1.2) ×(-6)
(3).4×(-5)
(4). (-6) ×(-2)
9、有理数除法法则
两数相除,
同号得“+”,
异号得“-”
并把绝对值相除。10、乘方法则
正数的任何次幂都是正数
负数的奇次幂得“-”
负数的偶次幂得“+”
混合运算的次序先乘方
再×÷
最后算+-
有括号的先算括号内
同级运算:从左向右第二章 有理数及其运算(1) 数轴相反数绝对值有关概念大小比较运算方法运算律运算有理数有理数的两种分类: 正整数
整数 0
有理数 负整数
正分数
分数
负分数 正整数
正有理数
正分数
有理数 0
负整数
负有理数
负分数数轴:规定了原点、正方向、单位长度的直线叫做数轴。
任何一个有理数都可以用数轴上的一个点来表示。
数轴上的点和有理数是一一对应的。如上图:
A点表示__;
B点表示__;
C点表示__;
D点表示__:
E点表示__。相反数:
只有符号不同的两个数互为相反数。
0的相反数是0。
例如:2和-2
互为相反数的两个数相加得0。
例如:5+(-5)=0
一个数 相反数是 。
例如: 3的相反数是-3
-4的相反数是-(-4)=4
倒数:
乘积是1的两个数互为倒数。
0没有倒数。
的倒数是 。绝对值:
从数轴上看,一个数的绝对值就是表示这个数的点离开原点的距离。数 的绝对值记为 。
正数的绝对值是它本身;
0的绝对值是0;
负数的绝对值是它的相反数。
即:例如:
有理数的大小比较:
正数都大于0,负数都小于0。即负数<0<正数。
数轴上两个点表示的数,右边的总比左边的大。
两个负数,绝对值大的反而小。有理数的运算方法:
1、加法:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。2、减法:
减去一个数,等于加上这个数的相反数。3、乘法:
两数相乘,同号得正,异号得负,绝对值相乘。
任何数与0相乘,积仍为0。
几个不为0的数相乘,当负因数有奇数个时,积为负;当负
因数有偶数个时,积为正。4、除法:
除以一个数等于乘以这个数的倒数。
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不为0的数,都得0。5、乘方:
求几个相同因数的积的运算,叫做乘方。
乘方运算可以化为乘法运算进行:
即:正数的任何次幂都是正数。
负数的奇数次幂是负数,偶数次幂是正数。
0的任何次幂都是0。 是底数, 是指数, 是幂。运算律:
1、加法交换律:
2、加法结合律:
3、乘法交换律:
4、乘法结合律:
5、分配律:有理数混和运算的运算顺序:
先算乘方,再算乘除,最后算加减。如果有括号就先算括号里面的。注意:同级运算要由左到右进行。测试:
1、一个数的绝对值是6.5,这个数是____。
2、绝对值小于3的非负整数是_______。
3、 的相反数的倒数是_____。
4、 _____。
5、如果 ,那么 。
6、
7、计算:
(1)
(2)苏科版初一数学第二章 有理数的复习学习目标1、复习有理数的混合运算及其解题技巧。
2、学会用数学思想解决实际问题的方法,从而体会数学存在的价值。主要知识点回顾有理数的加减法法则是什么?
有理数的乘法法则是什么?
有理数的除法法则是什么?
有理数乘方的符号法则是什么?
你学过哪些运算律?
什么是科学记数法?
有理数混合运算的顺序是什么?
友情提醒同号两数相加,取相同的符号,并把绝对值相加;
异号两数相加,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值。互为相反数相加得0;
一个数与零相加,仍得这个数;
减去一个数就等于加上这个数的相反数;两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与0相乘都得0;
几个不等于0的因数相乘,积的符号由负因数的个数的决定。当负因数有奇数个时,积为负;当负因数有偶数个时,积为正;
几个因数相乘,若有一个因数为0,则结果为0;除以一个数就等于乘以这个数的倒数;
0除以任何一个不等于0的数,都得0;
两数相除,同号得正,异号得负,并把绝对值相除;正数的任何次幂都是正数;
负数的奇数次幂是负数,负数的偶次幂是正数;加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a?b=b?a
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c-d)=ab+ac-ad把一个大于10的数写成a×10n的形式,其中1≤a<10,n是正整数,这种记数的方法称为科学记数法。有理数混合运算顺序是1、先算乘方,后算乘除,最后算加减,有括号先算括号里面的;2、同级运算必须按照从左到右的顺序进行;练一练:计算例题讲析例1:观察下列解题过程,计算:
解:设s= (1) 则由(2)-(1)得2s=所以s=通过阅读,请你用学到的方法计算:例2:计算例3:看一看猜一猜:请阅读下列材料《西游记》中有这么一段:话说悟空惹恼了师傅唐僧,唐僧便念起金箍咒来,痛得悟空抱头叫嚷:“疼死我也”。假如悟空头上的金箍咒缩短了1cm,那么金箍咒要陷进头皮多么毫米?(π取3.14,结果保留两位小数)例4:详解:设戴在悟空头上的金箍咒的半径为R,收缩后的小圆的半径为r,由题意得:
2π (R – r)= 1
R – r =≈ 0.16(mm)答:略例5:古时候某个王国里有一位聪明的大臣,他发明了国际象棋献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求。大臣说:“就在这个棋盘上放些米粒吧,第1格放1粒,第2格放2粒,第3格放4粒,第4格放8粒,然后依次为16粒,32粒……直到第64格。”“你真傻,就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您国库里没有这么多米。”你认为国王的国库里有这么多米吗? 若10000粒米为1斤,100斤为1麻袋,那么这位大臣要的大米约合多少麻袋呢?友情提醒仔细想想,你准行的哟
解:根据题意,得:
同学们再见!
两个数叫做互为相反数 若xy互为相反数,
则x+y=0一个正数的绝对值是它本身
一个负数的绝对值是它的相反数
0的绝对值是0___________的绝对值是它本身
___________绝对值是它的相反数5、绝对值法则6、有理数加法法则
(1)同号两数相加,取原来的符号
并把绝对值相加;
(2)异号两数相加,取绝对值较大
的数的符号,并用较大的绝对值
减去较小的绝对值。
(3) 0加一个数还得这个数7、有理数减法法则
减去一个数等于加上这个数的相反数即:a-b=a+(-b)口答(1)-4+(-6)
(2)-8+2
(3) +3+(-5)+(-3)
(4) -7-4+58、有理数乘法法则
两数相乘,
同号得“+”,
异号得“-”
并把绝对值相乘。口 答(1). -2×(+3)
(2).(-1.2) ×(-6)
(3).4×(-5)
(4). (-6) ×(-2)
9、有理数除法法则
两数相除,
同号得“+”,
异号得“-”
并把绝对值相除。10、乘方法则
正数的任何次幂都是正数
负数的奇次幂得“-”
负数的偶次幂得“+”
混合运算的次序先乘方
再×÷
最后算+-
有括号的先算括号内
同级运算:从左向右第二章 有理数及其运算(1) 数轴相反数绝对值有关概念大小比较运算方法运算律运算有理数有理数的两种分类: 正整数
整数 0
有理数 负整数
正分数
分数
负分数 正整数
正有理数
正分数
有理数 0
负整数
负有理数
负分数数轴:规定了原点、正方向、单位长度的直线叫做数轴。
任何一个有理数都可以用数轴上的一个点来表示。
数轴上的点和有理数是一一对应的。如上图:
A点表示__;
B点表示__;
C点表示__;
D点表示__:
E点表示__。相反数:
只有符号不同的两个数互为相反数。
0的相反数是0。
例如:2和-2
互为相反数的两个数相加得0。
例如:5+(-5)=0
一个数 相反数是 。
例如: 3的相反数是-3
-4的相反数是-(-4)=4
倒数:
乘积是1的两个数互为倒数。
0没有倒数。
的倒数是 。绝对值:
从数轴上看,一个数的绝对值就是表示这个数的点离开原点的距离。数 的绝对值记为 。
正数的绝对值是它本身;
0的绝对值是0;
负数的绝对值是它的相反数。
即:例如:
有理数的大小比较:
正数都大于0,负数都小于0。即负数<0<正数。
数轴上两个点表示的数,右边的总比左边的大。
两个负数,绝对值大的反而小。有理数的运算方法:
1、加法:
同号两数相加,取相同的符号,并把绝对值相加。
异号两数相加,取绝对值大的数的符号,并用较大的绝对值减去较小的绝对值。
一个数同0相加,仍得这个数。2、减法:
减去一个数,等于加上这个数的相反数。3、乘法:
两数相乘,同号得正,异号得负,绝对值相乘。
任何数与0相乘,积仍为0。
几个不为0的数相乘,当负因数有奇数个时,积为负;当负
因数有偶数个时,积为正。4、除法:
除以一个数等于乘以这个数的倒数。
两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不为0的数,都得0。5、乘方:
求几个相同因数的积的运算,叫做乘方。
乘方运算可以化为乘法运算进行:
即:正数的任何次幂都是正数。
负数的奇数次幂是负数,偶数次幂是正数。
0的任何次幂都是0。 是底数, 是指数, 是幂。运算律:
1、加法交换律:
2、加法结合律:
3、乘法交换律:
4、乘法结合律:
5、分配律:有理数混和运算的运算顺序:
先算乘方,再算乘除,最后算加减。如果有括号就先算括号里面的。注意:同级运算要由左到右进行。测试:
1、一个数的绝对值是6.5,这个数是____。
2、绝对值小于3的非负整数是_______。
3、 的相反数的倒数是_____。
4、 _____。
5、如果 ,那么 。
6、
7、计算:
(1)
(2)苏科版初一数学第二章 有理数的复习学习目标1、复习有理数的混合运算及其解题技巧。
2、学会用数学思想解决实际问题的方法,从而体会数学存在的价值。主要知识点回顾有理数的加减法法则是什么?
有理数的乘法法则是什么?
有理数的除法法则是什么?
有理数乘方的符号法则是什么?
你学过哪些运算律?
什么是科学记数法?
有理数混合运算的顺序是什么?
友情提醒同号两数相加,取相同的符号,并把绝对值相加;
异号两数相加,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值。互为相反数相加得0;
一个数与零相加,仍得这个数;
减去一个数就等于加上这个数的相反数;两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与0相乘都得0;
几个不等于0的因数相乘,积的符号由负因数的个数的决定。当负因数有奇数个时,积为负;当负因数有偶数个时,积为正;
几个因数相乘,若有一个因数为0,则结果为0;除以一个数就等于乘以这个数的倒数;
0除以任何一个不等于0的数,都得0;
两数相除,同号得正,异号得负,并把绝对值相除;正数的任何次幂都是正数;
负数的奇数次幂是负数,负数的偶次幂是正数;加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a?b=b?a
乘法结合律:(ab)c=a(bc)
乘法分配律:a(b+c-d)=ab+ac-ad把一个大于10的数写成a×10n的形式,其中1≤a<10,n是正整数,这种记数的方法称为科学记数法。有理数混合运算顺序是1、先算乘方,后算乘除,最后算加减,有括号先算括号里面的;2、同级运算必须按照从左到右的顺序进行;练一练:计算例题讲析例1:观察下列解题过程,计算:
解:设s= (1) 则由(2)-(1)得2s=所以s=通过阅读,请你用学到的方法计算:例2:计算例3:看一看猜一猜:请阅读下列材料《西游记》中有这么一段:话说悟空惹恼了师傅唐僧,唐僧便念起金箍咒来,痛得悟空抱头叫嚷:“疼死我也”。假如悟空头上的金箍咒缩短了1cm,那么金箍咒要陷进头皮多么毫米?(π取3.14,结果保留两位小数)例4:详解:设戴在悟空头上的金箍咒的半径为R,收缩后的小圆的半径为r,由题意得:
2π (R – r)= 1
R – r =≈ 0.16(mm)答:略例5:古时候某个王国里有一位聪明的大臣,他发明了国际象棋献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求。大臣说:“就在这个棋盘上放些米粒吧,第1格放1粒,第2格放2粒,第3格放4粒,第4格放8粒,然后依次为16粒,32粒……直到第64格。”“你真傻,就要这么一点米粒?!”国王哈哈大笑,大臣说:“就怕您国库里没有这么多米。”你认为国王的国库里有这么多米吗? 若10000粒米为1斤,100斤为1麻袋,那么这位大臣要的大米约合多少麻袋呢?友情提醒仔细想想,你准行的哟
解:根据题意,得:
同学们再见!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
