北师大版数学七年级下册 4.2图形的全等 课件 (共16张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 4.2图形的全等 课件 (共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
第四章 三角形
4.2 图形的全等
知识点 全等图形
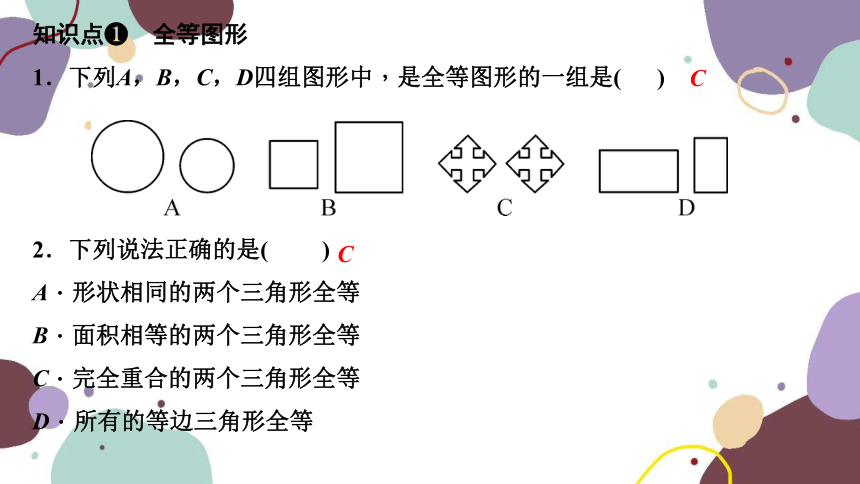
1.下列A,B,C,D四组图形中,是全等图形的一组是( )
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
C
C
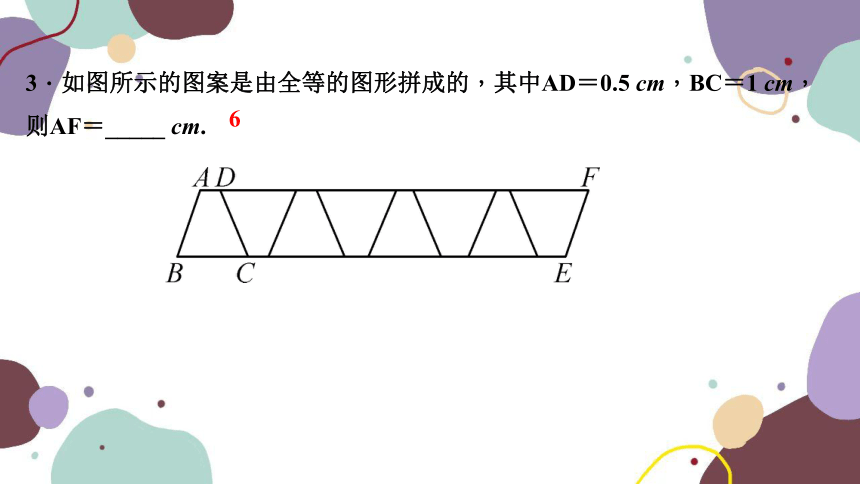
3.如图所示的图案是由全等的图形拼成的,其中AD=0.5 cm,BC=1 cm,则AF=_____ cm.
6
知识点 全等三角形及性质
4.若△ABC≌△MNP,∠A=∠M,∠C=∠P,AB=4 cm,BC=2 cm,则NP=( )
A.2 cm B.3 cm C.4 cm D.6 cm
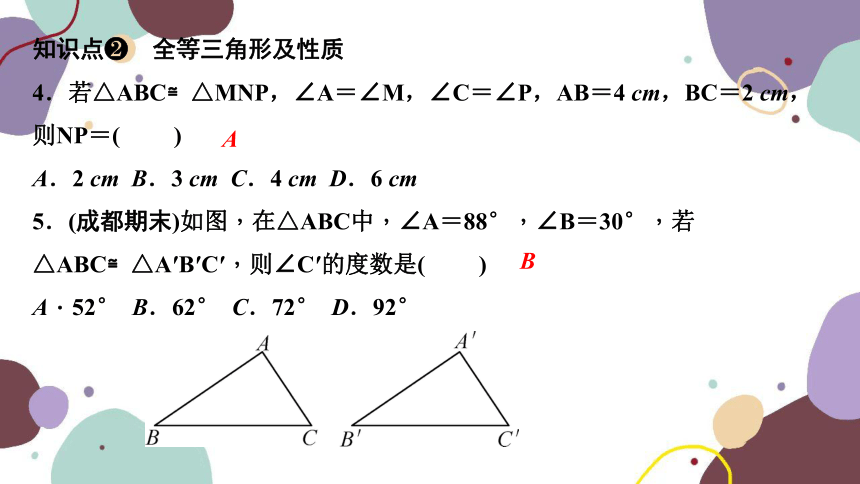
5.(成都期末)如图,在△ABC中,∠A=88°,∠B=30°,若△ABC≌△A′B′C′,则∠C′的度数是( )
A.52° B.62° C.72° D.92°
A
B
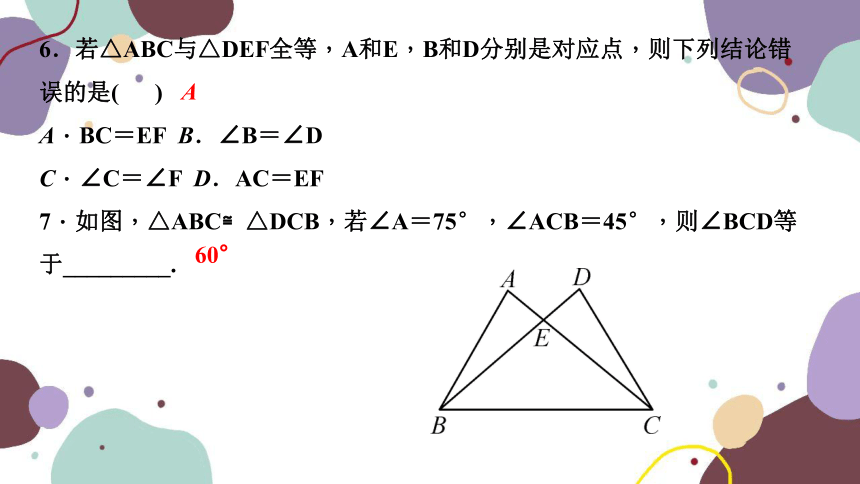
6.若△ABC与△DEF全等,A和E,B和D分别是对应点,则下列结论错误的是( )
A.BC=EF B.∠B=∠D
C.∠C=∠F D.AC=EF
7.如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于_________.
A
60°
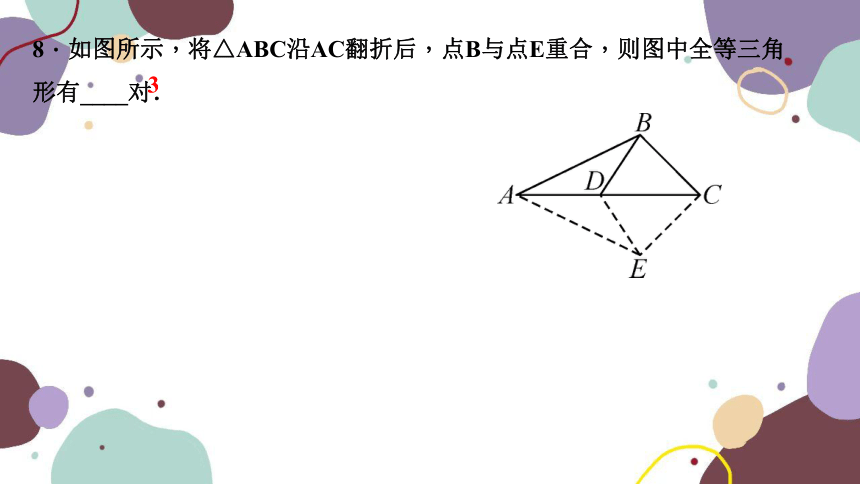
8.如图所示,将△ABC沿AC翻折后,点B与点E重合,则图中全等三角形有____对.
3
9.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出边FG的对应边与∠EGF的对应角;
(2)若EF=2.1 cm,FH=1.1 cm,HM=3.3 cm,求MN和HG的长度.
解:(1)∵△EFG≌△NMH,
∴FG的对应边是MH,∠EGF的对应角是∠NHM
(2)∵△EFG≌△NMH,
∴MN=EF=2.1 cm,HM=FG=3.3 cm,
∵FH=1.1 cm,
∴HG=3.3-1.1=2.2(cm)
10.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:①AC=AF;②EF=BC;③∠FAB=∠EAB;④∠EAB=∠FAC,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
B
11.如图,D,E分别为△ABC的AC,BC边上的中点,DE∥AB,将此三角形沿DE折叠,使点C落在边AB上的点P处.若∠CDE=48°,则∠APD等于( )
A.42° B.48° C.52° D.58°
B
12.如果△ABC≌△AED,并且AC=6 cm,BC=5 cm,△ABC的周长为18 cm,则AE=____cm.
13.如图所示,△ABC≌△ADE,BC的延长线交DA于F点,交DE于G点,∠ACB=105°,∠CAD=15°,∠B=30°,则∠1的度数为_____度.
7
60
14.(巴中期末)如图,已知△ABC≌△ABD,∠CAB=45°,∠CBD=40°,求∠D的度数.
解:∵△ABC≌△ABD,∠CAB=45°,
∴∠DAB=∠CAB=45°,∠ABC=∠ABD,
∵∠CBD=40°,
∴∠DBA=20°,
∴∠D=180°-∠DAB-∠DBA=115°
15.如图,A,E,F,C在一条直线上,△AED≌△CFB,试说明DE∥BF.
解:∵△AED≌△CFB,
∴∠AED=∠CFB,
∵∠AED+∠DEF=∠CFB+∠EFB=180°,
∴∠DEF=∠EFB,
∴DE∥BF
16.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2 cm,BC=3 cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.
解:(1)∵△ABD≌△EBC,
∴BD=BC=3 cm,BE=AB=2 cm,
∴DE=BD-BE=1 cm
(2)DB与AC垂直,理由:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A,B,C在一条直线上,
∴∠EBC=90°,∴DB与AC垂直
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD
第四章 三角形
4.2 图形的全等
知识点 全等图形
1.下列A,B,C,D四组图形中,是全等图形的一组是( )
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
C
C
3.如图所示的图案是由全等的图形拼成的,其中AD=0.5 cm,BC=1 cm,则AF=_____ cm.
6
知识点 全等三角形及性质
4.若△ABC≌△MNP,∠A=∠M,∠C=∠P,AB=4 cm,BC=2 cm,则NP=( )
A.2 cm B.3 cm C.4 cm D.6 cm
5.(成都期末)如图,在△ABC中,∠A=88°,∠B=30°,若△ABC≌△A′B′C′,则∠C′的度数是( )
A.52° B.62° C.72° D.92°
A
B
6.若△ABC与△DEF全等,A和E,B和D分别是对应点,则下列结论错误的是( )
A.BC=EF B.∠B=∠D
C.∠C=∠F D.AC=EF
7.如图,△ABC≌△DCB,若∠A=75°,∠ACB=45°,则∠BCD等于_________.
A
60°
8.如图所示,将△ABC沿AC翻折后,点B与点E重合,则图中全等三角形有____对.
3
9.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出边FG的对应边与∠EGF的对应角;
(2)若EF=2.1 cm,FH=1.1 cm,HM=3.3 cm,求MN和HG的长度.
解:(1)∵△EFG≌△NMH,
∴FG的对应边是MH,∠EGF的对应角是∠NHM
(2)∵△EFG≌△NMH,
∴MN=EF=2.1 cm,HM=FG=3.3 cm,
∵FH=1.1 cm,
∴HG=3.3-1.1=2.2(cm)
10.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,则下列结论:①AC=AF;②EF=BC;③∠FAB=∠EAB;④∠EAB=∠FAC,其中正确结论的个数是( )
A.4个 B.3个 C.2个 D.1个
B
11.如图,D,E分别为△ABC的AC,BC边上的中点,DE∥AB,将此三角形沿DE折叠,使点C落在边AB上的点P处.若∠CDE=48°,则∠APD等于( )
A.42° B.48° C.52° D.58°
B
12.如果△ABC≌△AED,并且AC=6 cm,BC=5 cm,△ABC的周长为18 cm,则AE=____cm.
13.如图所示,△ABC≌△ADE,BC的延长线交DA于F点,交DE于G点,∠ACB=105°,∠CAD=15°,∠B=30°,则∠1的度数为_____度.
7
60
14.(巴中期末)如图,已知△ABC≌△ABD,∠CAB=45°,∠CBD=40°,求∠D的度数.
解:∵△ABC≌△ABD,∠CAB=45°,
∴∠DAB=∠CAB=45°,∠ABC=∠ABD,
∵∠CBD=40°,
∴∠DBA=20°,
∴∠D=180°-∠DAB-∠DBA=115°
15.如图,A,E,F,C在一条直线上,△AED≌△CFB,试说明DE∥BF.
解:∵△AED≌△CFB,
∴∠AED=∠CFB,
∵∠AED+∠DEF=∠CFB+∠EFB=180°,
∴∠DEF=∠EFB,
∴DE∥BF
16.如图,点A,B,C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2 cm,BC=3 cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由;
(3)判断直线AD与直线CE的位置关系,并说明理由.
解:(1)∵△ABD≌△EBC,
∴BD=BC=3 cm,BE=AB=2 cm,
∴DE=BD-BE=1 cm
(2)DB与AC垂直,理由:
∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A,B,C在一条直线上,
∴∠EBC=90°,∴DB与AC垂直
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
