江西省井冈山中学2012-2013学年高二第四次月考数学(文)试题
文档属性
| 名称 | 江西省井冈山中学2012-2013学年高二第四次月考数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 341.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-16 00:00:00 | ||
图片预览



文档简介
考生注意:
本试卷设Ⅰ、Ⅱ卷和答题卡纸三部分,试卷所有答案都必须写在答题纸上。
答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位。
考试时间为120分钟,试卷满分为150分。
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分)
1.抛物线的焦点坐标为( )
A. B.(1,0) C.(0,-)D.(-,0)21世纪教育网
2.设l,m,n为三条不同的直线,α、β为两个不同的平面,下列命题中正确的个数是( )
① 若l⊥α,m∥β,α⊥β则l⊥m ② 若则l⊥α
③ 若l∥m,m∥n,l⊥α,则n⊥α ④ 若l∥m,m⊥α,n⊥β,α∥β,则l∥n
A. 1 B. 2 C. 3 D. 4
3.将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线与是异面直线的是 ……………………………………………( )
A.①② B.②④ C.①④ D.①③
4.一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A. B. C. D.
5.如图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且==,则( )
(A)EF与GH互相平行
(B)EF与GH异面
(C)EF与GH的交点M可能在直线AC上,也可能不在直线AC上
(D)EF与GH的交点M一定在直线AC上
6.已知正四棱锥的侧棱长与底面边长都相等,是的中点,则所成的角的余弦值为( )
A. B. C. D.
7.椭圆的一条弦被平分,那么这条弦所在的直线方程是 ( )
A. B. C. D.
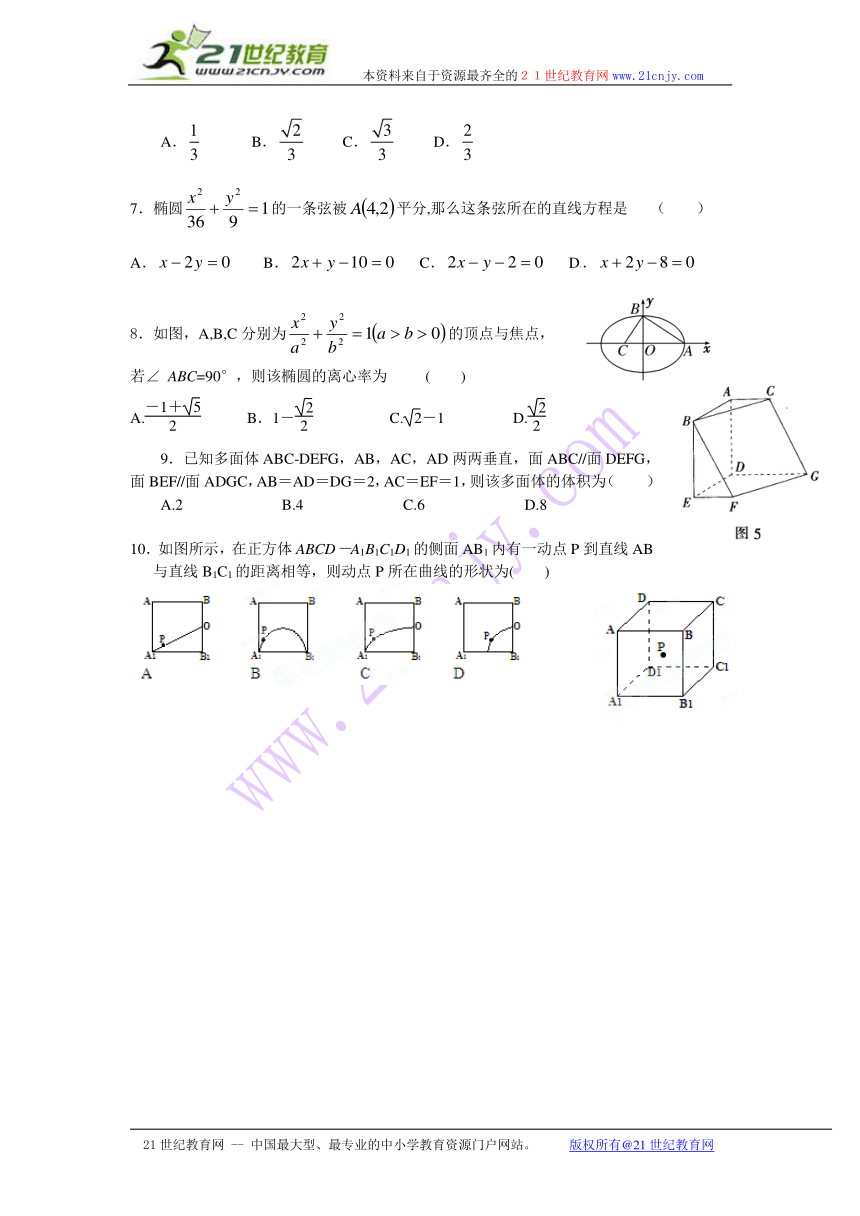
8.如图,A,B,C分别为的顶点与焦点,
若∠ ABC=90°,则该椭圆的离心率为 ( )
A. B.1- C.-1 D.
9.已知多面体ABC-DEFG,AB,AC,AD两两垂直,面ABC//面DEFG,面BEF//面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )
A.2 B.4 C.6 D.8
[21世纪教育网
10.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线AB与直线B1C1的距离相等,则动点P所在曲线的形状为( )
21世纪教育网
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题5分,共25分)
11.三条平行直线可以确定平面_________个
12.已知,若直线过点,且与线段相交,则直线的斜率取值范围是_____________。
13.如图是一个空间几何体的三视图,则该几何体的外接球的表面积为 .
14.设F1、F2分别是椭圆+=1的左、右焦点,P为椭圆上
任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
15.正的中线AF与中位线DE相交于G,已知是绕边DE旋转过程中的一个图形,给出四个命题:
①动点在上的射影在线段上;[来源:学科网21世纪教育网]
②恒有;
③三棱锥的体积有最大值; [来源:21世纪教育网]
④异面直线与不可能垂直.[来源:Z#xx#k.Com]
以上正确的命题序号是 ;
三、解答题(本大题共6个小题,共75分)
16.一个多面体的直观图和三视图如下:(其中分别是中点)
(1)求证:平面;
(2)求多面体的体积.
17.设函数
(1)设的内角,且为钝角,求的最小值;
(2)设是锐角的内角,且求 的三个内角的大小和AC边的长。
18.如图,四面体ABCD中,O、E分别是BD、BC的中点,
(I)求证:平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。
19. 已知双曲线C的中心在原点,抛物线的焦点是双曲线C的一个焦点,且双曲线经过点,又知直线与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若,求实数k值.
20.如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面平面;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
21.如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.
(1)设N为EF上一点,当时,有DN ∥平面AEM,求 的值;
(2)试探究点M的位置,使平面AME⊥平面AEF。
答案:
16 解:
(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,且,
,∴. ---2分
取中点,连,由分别是中点,可设:,
∴面面 ∴面… ---8分
(2)作于,由于三棱柱为直三棱柱
∴面,
且 ∴,---12
在△中,由正弦定理得: ……12分
18(本题满分12分)
解:(I)证明:连结OC
在中,由已知可得
而 即
平面
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在中,
19. 解:(1)抛物线的焦点是(),则双曲线的.………………1分
设双曲线方程:…………………………2分
解得:…………………………5分
20. 解:(1) [21世纪教育网]
(2)取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1=A1D1时,EH∥平面FGB1.
(3)∵EH∥平面FGB1,∴VE—FGB1=VH—FGB1,
而VH—FGB1=VG—HFB1=×1×S△HFB1,
S△HFB1=S梯形B1C1D1H-S△B1C1F-S△D1HF=,
[来源:21世纪教育网]
本试卷设Ⅰ、Ⅱ卷和答题卡纸三部分,试卷所有答案都必须写在答题纸上。
答题纸与试卷在试题编号上是一一对应的,答题时应特别注意,不能错位。
考试时间为120分钟,试卷满分为150分。
第Ⅰ卷(选择题 共50分)
一、选择题(本大题共10小题,每小题5分,共50分)
1.抛物线的焦点坐标为( )
A. B.(1,0) C.(0,-)D.(-,0)21世纪教育网
2.设l,m,n为三条不同的直线,α、β为两个不同的平面,下列命题中正确的个数是( )
① 若l⊥α,m∥β,α⊥β则l⊥m ② 若则l⊥α
③ 若l∥m,m∥n,l⊥α,则n⊥α ④ 若l∥m,m⊥α,n⊥β,α∥β,则l∥n
A. 1 B. 2 C. 3 D. 4
3.将下面的平面图形(每个点都是正三角形的顶点或边的中点)沿虚线折成一个正四面体后,直线与是异面直线的是 ……………………………………………( )
A.①② B.②④ C.①④ D.①③
4.一个圆柱的侧面积展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )
A. B. C. D.
5.如图,在空间四边形ABCD中,点E、H分别是边AB、AD的中点,F、G分别是边BC、CD上的点,且==,则( )
(A)EF与GH互相平行
(B)EF与GH异面
(C)EF与GH的交点M可能在直线AC上,也可能不在直线AC上
(D)EF与GH的交点M一定在直线AC上
6.已知正四棱锥的侧棱长与底面边长都相等,是的中点,则所成的角的余弦值为( )
A. B. C. D.
7.椭圆的一条弦被平分,那么这条弦所在的直线方程是 ( )
A. B. C. D.
8.如图,A,B,C分别为的顶点与焦点,
若∠ ABC=90°,则该椭圆的离心率为 ( )
A. B.1- C.-1 D.
9.已知多面体ABC-DEFG,AB,AC,AD两两垂直,面ABC//面DEFG,面BEF//面ADGC,AB=AD=DG=2,AC=EF=1,则该多面体的体积为( )
A.2 B.4 C.6 D.8
[21世纪教育网
10.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线AB与直线B1C1的距离相等,则动点P所在曲线的形状为( )
21世纪教育网
第Ⅱ卷(非选择题 共100分)
二、填空题(本大题共5小题,每小题5分,共25分)
11.三条平行直线可以确定平面_________个
12.已知,若直线过点,且与线段相交,则直线的斜率取值范围是_____________。
13.如图是一个空间几何体的三视图,则该几何体的外接球的表面积为 .
14.设F1、F2分别是椭圆+=1的左、右焦点,P为椭圆上
任一点,点M的坐标为(6,4),则|PM|+|PF1|的最大值为_______
15.正的中线AF与中位线DE相交于G,已知是绕边DE旋转过程中的一个图形,给出四个命题:
①动点在上的射影在线段上;[来源:学科网21世纪教育网]
②恒有;
③三棱锥的体积有最大值; [来源:21世纪教育网]
④异面直线与不可能垂直.[来源:Z#xx#k.Com]
以上正确的命题序号是 ;
三、解答题(本大题共6个小题,共75分)
16.一个多面体的直观图和三视图如下:(其中分别是中点)
(1)求证:平面;
(2)求多面体的体积.
17.设函数
(1)设的内角,且为钝角,求的最小值;
(2)设是锐角的内角,且求 的三个内角的大小和AC边的长。
18.如图,四面体ABCD中,O、E分别是BD、BC的中点,
(I)求证:平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。
19. 已知双曲线C的中心在原点,抛物线的焦点是双曲线C的一个焦点,且双曲线经过点,又知直线与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若,求实数k值.
20.如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面平面;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
21.如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.
(1)设N为EF上一点,当时,有DN ∥平面AEM,求 的值;
(2)试探究点M的位置,使平面AME⊥平面AEF。
答案:
16 解:
(1)由三视图知,该多面体是底面为直角三角形的直三棱柱,且,
,∴. ---2分
取中点,连,由分别是中点,可设:,
∴面面 ∴面… ---8分
(2)作于,由于三棱柱为直三棱柱
∴面,
且 ∴,---12
在△中,由正弦定理得: ……12分
18(本题满分12分)
解:(I)证明:连结OC
在中,由已知可得
而 即
平面
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在中,
19. 解:(1)抛物线的焦点是(),则双曲线的.………………1分
设双曲线方程:…………………………2分
解得:…………………………5分
20. 解:(1) [21世纪教育网]
(2)取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1=A1D1时,EH∥平面FGB1.
(3)∵EH∥平面FGB1,∴VE—FGB1=VH—FGB1,
而VH—FGB1=VG—HFB1=×1×S△HFB1,
S△HFB1=S梯形B1C1D1H-S△B1C1F-S△D1HF=,
[来源:21世纪教育网]
同课章节目录
