菱形(1)
图片预览
文档简介
菱形(1)
执 笔: 姜尘 初审: 复审:
授课人: 课型: 新课 课时: 第一课时
学生姓名: 班级: 小组:
学习目标:
1理解并掌握菱形的定义及性质定理1、2。
2 会用菱形的性质定理解决有关问题
学习重点: 菱形的性质定理1、2。
学习难点:定理的证明方法及运用。
自主探究
一,导引自学
1.什么叫矩形?平行四边形和矩形之间的关系是什么?
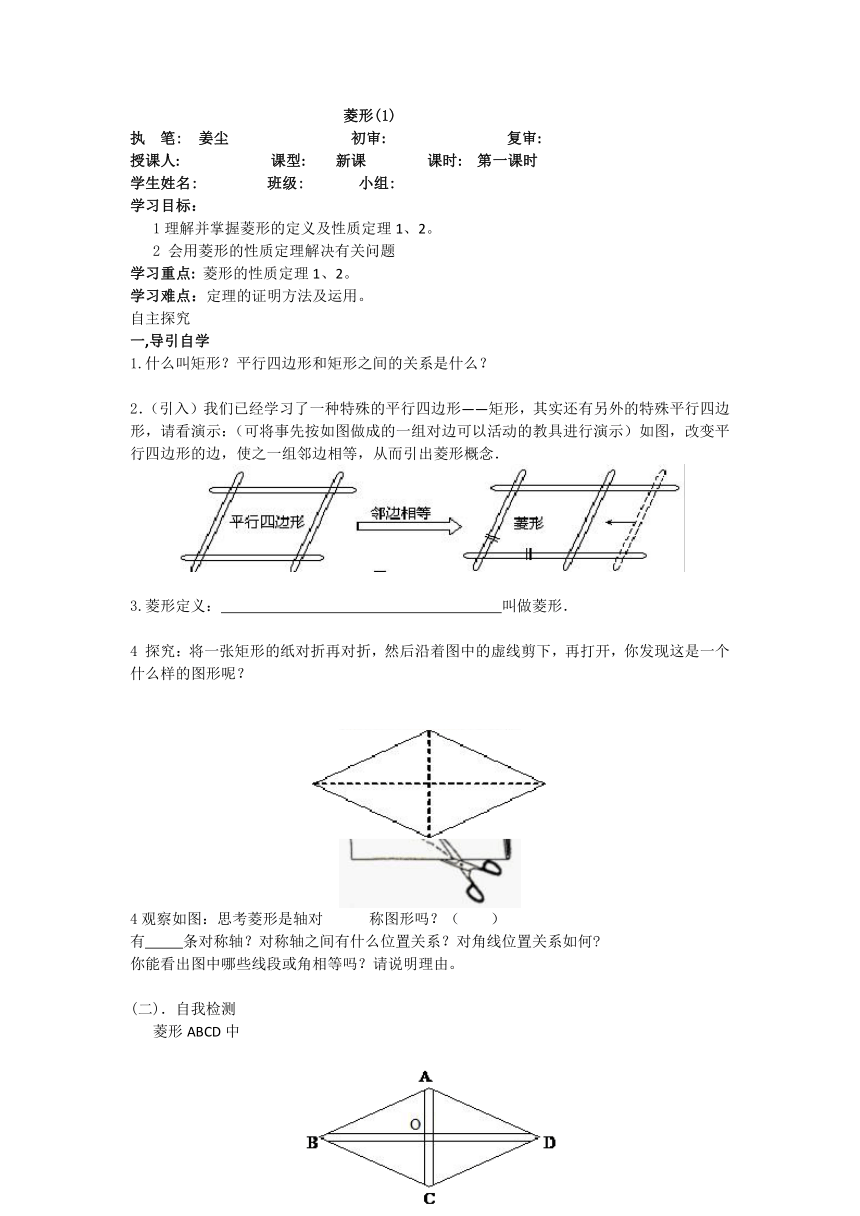
2.(引入)我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形,请看演示:(可将事先按如图做成的一组对边可以活动的教具进行演示)如图,改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.
3.菱形定义: 叫做菱形.
4 探究:将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,再打开,你发现这是一个什么样的图形呢?
4观察如图:思考菱形是轴对 称图形吗?( )
有 条对称轴?对称轴之间有什么位置关系?对角线位置关系如何?
你能看出图中哪些线段或角相等吗?请说明理由。
(二).自我检测
菱形ABCD中
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
三 知新有疑
通过自学,我又知道了:
但还有困惑:
交流展示
菱形性质(1)菱形的四条边都相等;(2)菱形的对角线___________并且每一条对角线平分______(3)菱形是特殊的____________
例题精析
例1: 如图是菱形花坛ABCD,它的边长为40m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2).
例2:如图,四边形ABCD是菱形. 对角线AC=8㎝,DB=6㎝,DH⊥AB与H.求DH的长.
达标测评:
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
2.菱形的两条对角线的长分别是6cm和8cm,则其周长为 ,面积为 .
3.菱形的一个内角为 ,且平分这个内角的对角线长为8cm,则这个菱形的周长为 .
4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
作业:
P105 5
2.已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
3.已知如图,菱形ABCD中,∠ADC=120°,AC=㎝,
(1)求BD的长;(2)求菱形ABCD的面积,
(3)写出A、B、C、D的坐标.
小结反思:
通过本节课的探究学习,我又有了新的收获和体验
知识与技能方面:
数学思想方法
学习感受反思
执 笔: 姜尘 初审: 复审:
授课人: 课型: 新课 课时: 第一课时
学生姓名: 班级: 小组:
学习目标:
1理解并掌握菱形的定义及性质定理1、2。
2 会用菱形的性质定理解决有关问题
学习重点: 菱形的性质定理1、2。
学习难点:定理的证明方法及运用。
自主探究
一,导引自学
1.什么叫矩形?平行四边形和矩形之间的关系是什么?
2.(引入)我们已经学习了一种特殊的平行四边形——矩形,其实还有另外的特殊平行四边形,请看演示:(可将事先按如图做成的一组对边可以活动的教具进行演示)如图,改变平行四边形的边,使之一组邻边相等,从而引出菱形概念.
3.菱形定义: 叫做菱形.
4 探究:将一张矩形的纸对折再对折,然后沿着图中的虚线剪下,再打开,你发现这是一个什么样的图形呢?
4观察如图:思考菱形是轴对 称图形吗?( )
有 条对称轴?对称轴之间有什么位置关系?对角线位置关系如何?
你能看出图中哪些线段或角相等吗?请说明理由。
(二).自我检测
菱形ABCD中
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
三 知新有疑
通过自学,我又知道了:
但还有困惑:
交流展示
菱形性质(1)菱形的四条边都相等;(2)菱形的对角线___________并且每一条对角线平分______(3)菱形是特殊的____________
例题精析
例1: 如图是菱形花坛ABCD,它的边长为40m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m2).
例2:如图,四边形ABCD是菱形. 对角线AC=8㎝,DB=6㎝,DH⊥AB与H.求DH的长.
达标测评:
1.若菱形的边长等于一条对角线的长,则它的一组邻角的度数分别为 .
2.菱形的两条对角线的长分别是6cm和8cm,则其周长为 ,面积为 .
3.菱形的一个内角为 ,且平分这个内角的对角线长为8cm,则这个菱形的周长为 .
4.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。
作业:
P105 5
2.已知:如图,四边形ABCD是菱形,F是AB上一点,DF交AC于E.
求证:∠AFD=∠CBE.
3.已知如图,菱形ABCD中,∠ADC=120°,AC=㎝,
(1)求BD的长;(2)求菱形ABCD的面积,
(3)写出A、B、C、D的坐标.
小结反思:
通过本节课的探究学习,我又有了新的收获和体验
知识与技能方面:
数学思想方法
学习感受反思
