选择性必修二第一章磁场练习(word版含答案)
文档属性
| 名称 | 选择性必修二第一章磁场练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览



文档简介
粤教版(2019)选择性必修二 第一章 磁场
一、单选题
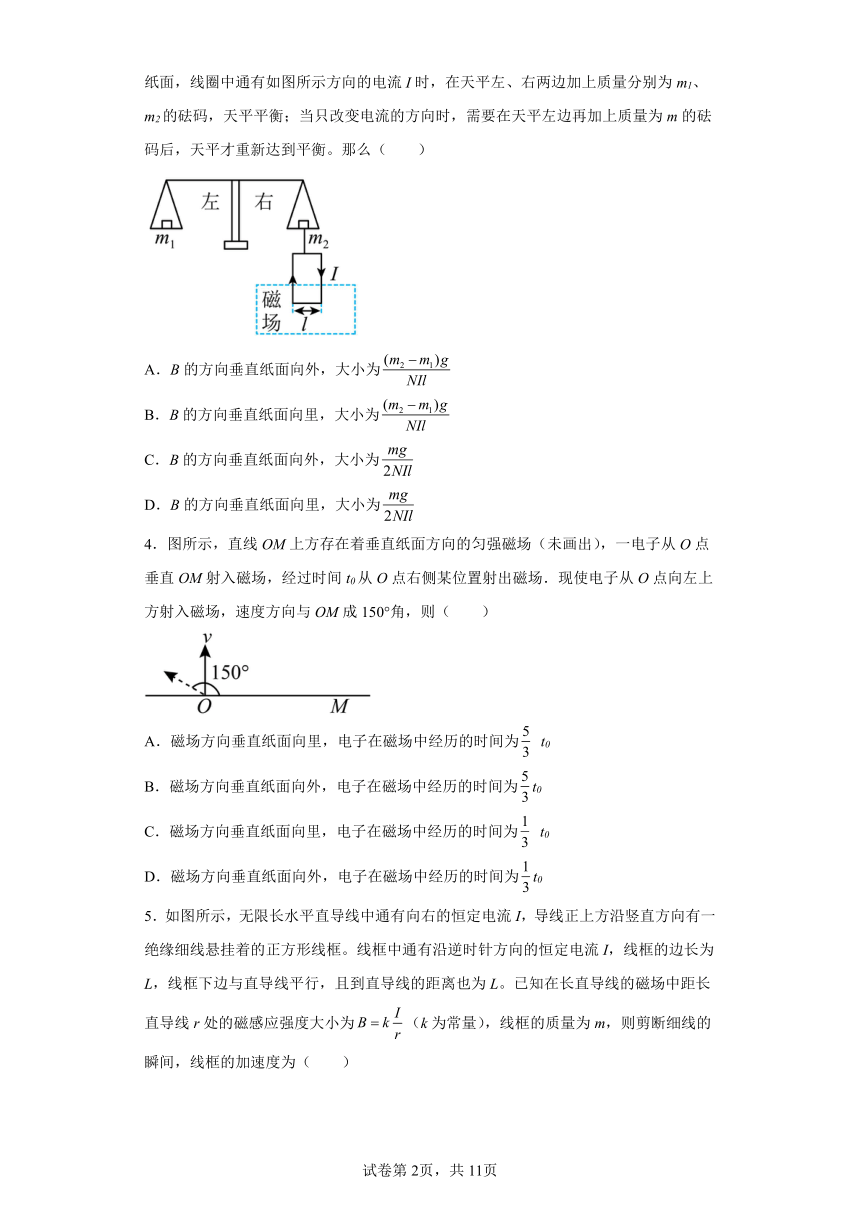
1.如图所示,一个静止的质量为m、带电荷量为q的粒子(不计重力),经电压U加速后垂直进入磁感应强度为B的匀强磁感中,粒子打至P点。设OP=x,能够正确反应x与U之间的函数关系的图象是( )
A. B.
C. D.
2.如图所示,abcd为边长为L的正方形,在四分之一圆abd区域内有垂直正方形平面向外的匀强磁场,磁场的磁感应强度为B。一个质量为m、电荷量为q的带电粒子从b点沿ba方向射入磁场,结果粒子恰好能通过c点,且射出磁场时的速度反向延长线通过a点,不计粒子的重力,则粒子的速度大小为( )
A. B. C. D.
3.如图所示装置,天平可以用来测定磁感应强度B的大小和方向,天平的右臂下面挂有一个共N匝的矩形线圈,线圈宽为l。线圈的下部悬在匀强磁场中,磁场方向垂直于纸面,线圈中通有如图所示方向的电流I时,在天平左、右两边加上质量分别为m1、m2的砝码,天平平衡;当只改变电流的方向时,需要在天平左边再加上质量为m的砝码后,天平才重新达到平衡。那么( )
A.B的方向垂直纸面向外,大小为
B.B的方向垂直纸面向里,大小为
C.B的方向垂直纸面向外,大小为
D.B的方向垂直纸面向里,大小为
4.图所示,直线OM上方存在着垂直纸面方向的匀强磁场(未画出),一电子从O点垂直OM射入磁场,经过时间t0从O点右侧某位置射出磁场.现使电子从O点向左上方射入磁场,速度方向与OM成150°角,则( )
A.磁场方向垂直纸面向里,电子在磁场中经历的时间为 t0
B.磁场方向垂直纸面向外,电子在磁场中经历的时间为t0
C.磁场方向垂直纸面向里,电子在磁场中经历的时间为 t0
D.磁场方向垂直纸面向外,电子在磁场中经历的时间为t0
5.如图所示,无限长水平直导线中通有向右的恒定电流I,导线正上方沿竖直方向有一绝缘细线悬挂着的正方形线框。线框中通有沿逆时针方向的恒定电流I,线框的边长为L,线框下边与直导线平行,且到直导线的距离也为L。已知在长直导线的磁场中距长直导线r处的磁感应强度大小为(k为常量),线框的质量为m,则剪断细线的瞬间,线框的加速度为( )
A.0 B. C. D.
6.如图,边长为l的正方形abcd内存在均匀磁场,磁感应度大小为B,方向垂直于纸面(abcd所在平面)向外。ab边中点有一电子发射源O,可向磁场内沿垂直于ab边的方向发射电子。已知电子的比荷为k,则从a、d两点射出的电子的速度大小分别为( )
A., B.,
C., D.,
7.如图所示,长方形abcd长ad = 0.6m,宽ab = 0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直纸面向里的匀强磁场(边界上无磁场),磁感应强度B = 0.25T。一群不计重力、质量m = 3 × 10 - 7kg、电荷量q = + 2 × 10 - 3C的带电粒子以速度v = 5 × 102m/s沿垂直ad方向且垂直于磁场射入磁场区域,则( )
A.从Od边射入的粒子,出射点全部分布在Oa边
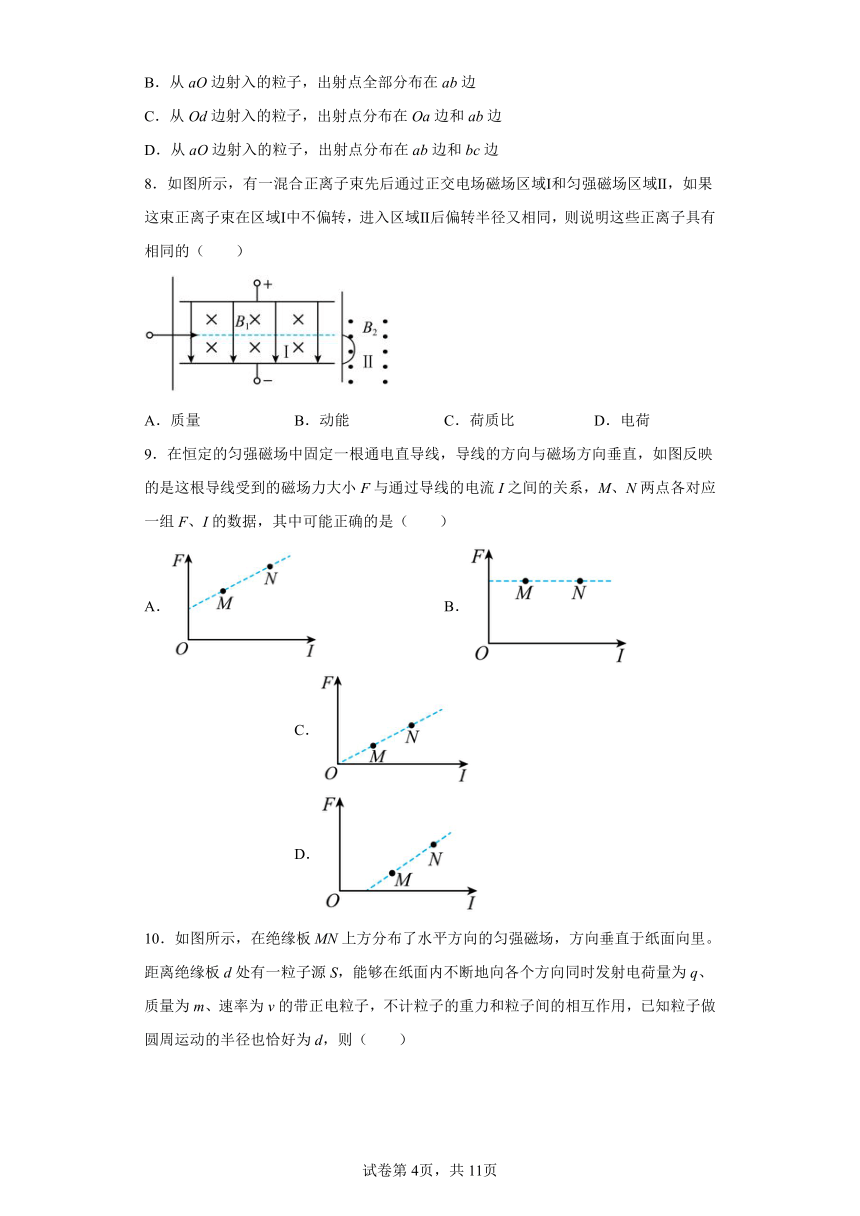
B.从aO边射入的粒子,出射点全部分布在ab边
C.从Od边射入的粒子,出射点分布在Oa边和ab边
D.从aO边射入的粒子,出射点分布在ab边和bc边
8.如图所示,有一混合正离子束先后通过正交电场磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径又相同,则说明这些正离子具有相同的( )
A.质量 B.动能 C.荷质比 D.电荷
9.在恒定的匀强磁场中固定一根通电直导线,导线的方向与磁场方向垂直,如图反映的是这根导线受到的磁场力大小F与通过导线的电流I之间的关系,M、N两点各对应一组F、I的数据,其中可能正确的是( )
A. B. C. D.
10.如图所示,在绝缘板MN上方分布了水平方向的匀强磁场,方向垂直于纸面向里。距离绝缘板d处有一粒子源S,能够在纸面内不断地向各个方向同时发射电荷量为q、质量为m、速率为v的带正电粒子,不计粒子的重力和粒子间的相互作用,已知粒子做圆周运动的半径也恰好为d,则( )
A.粒子能打到板上的区域长度为2d
B.能打到板上最左侧的粒子所用的时间为
C.粒子从发射到打到板上的最长时间为
D.同一时刻发射的粒子打到板上的最大时间差为
11.如图所示,在第一象限内存在着垂直纸面向里的匀强磁场。一质子从P点垂直磁场射入,射入时速度方向与x轴夹角为60°,质子从y轴上离开磁场时速度方向与y轴垂直。已知质子电荷量为e、质量为m,磁场磁感应强度大小为B,P点的坐标为,则( )
A.质子在磁场中运动的轨迹圆的圆心的坐标为
B.质子在磁场中运动的轨迹圆的半径
C.质子射入速度大小为
D.质子在磁场中运动的时间为
12.如图所示是一个水平放置的圆环形玻璃小槽,槽内光滑,槽宽度和深度处处相同.现将一直径略小于槽宽的带正电小球放在槽中,让它受绝缘棒打击后获得一初速度v0.与此同时,有一变化的磁场垂直穿过圆环形玻璃小槽外径所对应的圆面积,磁感应强度B的大小跟时间成正比,方向竖直向下.设小球在运动过程中所带电荷量不变,那么( )
A.小球受到的向心力大小不变
B.小球受到的向心力大小不断增加
C.洛伦兹力对小球做功
D.小球受到的洛伦兹力大小与时间成正比
13.如图所示,在半径为R的圆形区域内(圆心为O)有匀强磁场,磁感应强度为B,方向垂直于圆平面(未画出)。一群具有相同比荷的负离子以相同的速率由P点在纸平面内沿不同方向射入磁场中,发生偏转后又飞出磁场,若离子在磁场中运动的轨道半径大于R,则下列说法中正确的是(不计离子的重力)( )
A.从Q点飞出的离子在磁场中运动的时间最长
B.沿PQ方向射入的离子飞出时偏转角最大
C.所有离子飞出磁场时的动能一定相等
D.在磁场中运动时间最长的离子可能经过圆心O点
14.回旋加速器是用来加速带电粒子使它获得很大动能的装置,其核心部分是两个D型金属盒,置于匀强磁场中,两盒分别与高频电源相连。下列说法正确的是( )
A.粒子被加速后的最大速度与D型金属盒的半径无关
B.粒子被加速后的最大动能随高频电源的加速电压的增大而增大
C.高频电源频率由粒子的质量、电量和磁感应强度决定
D.高频电源频率与粒子的质量、电量和磁感应强度无关
15.如图所示,MN的右侧存在范围足够大、磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向里,MN右侧到MN的距离为L的O处有一个粒子源,可沿纸面内各个方向射出质量为m、电荷量为q的带正电粒子(不计重力及粒子间的相互作用),速度均为,则粒子在磁场中运动的最短时间为( )
A. B. C. D.
二、填空题
16.如图,上下两块金属板水平放置,相距为d,板间电压为U。两板间右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机喷嘴处在两板中线左侧位置,从喷嘴水平向右喷出质量为m、速度为v0的带电墨滴。墨滴在电场区域恰能做匀速直线运动,并垂直磁场左边界进入电场、磁场共存区域,最终垂直打在下板上。重力加速度为g,则墨滴带电量大小q=_______ ; 磁感应强度B=_________(均用题中物理量符号表示)。
17.导体棒中带电粒子的定向移动形成电流,电流可以从宏观和微观两个角度来认识,安培力与洛伦兹力也有宏观与微观的对应关系。
如图所示,静止不动的匀强磁场的磁感应强度大小为B,方向竖直向下。一段直导体棒长为L,横截面积为S,单位体积的自由电荷个数为n,自由电荷的电荷量为。导体棒中通有恒定电流,自由电荷的定向移动速率为(本题中两问均认为始终不变)。导体棒水平放置处于磁场中(垂直于磁感应强度)。
(1)若导体棒相对磁场静止,电荷定向运动时所受洛伦兹力的矢量和,在宏观上表现为导体棒所受的安培力。按照这个思路,请你由安培力的表达式推导出洛伦兹力大小的表达式。( )
(2)概念学习中,类比与比较是常用的学习方法。我们已经知道,垂直于匀强磁场磁感线的通电导线所受的安培力,由此,我们用来定义磁感应强度。同样,运动方向垂直于匀强磁场磁感线的带电粒子所受的洛伦兹力,由此也可用洛伦兹力来定义磁感应强度,定义式是_________,把该定义式与电场强度的定义式进行对比,两个定义式(而非物理量)的差别在于:__________________
18.如图,长度均为L的长直导体棒a、b平行置于光滑绝缘水平桌面,b棒固定,a棒与力传感器相连。当a、b中分别通以大小为Ia、Ib的恒定电流时,a棒静止,传感器受到a给它水平向左、大小为F的拉力。则a、b中的电流方向______(选填“相同”或“相反”),a中电流在b棒所在处产生的磁感应强度大小为______。
19.如图,在正方形中的区域内,存在方向垂直纸面向里的匀强磁场,区域内有方向平行的匀强电场(图中未画出)。现有一带电粒子(不计重力)从点沿方向射入磁场,随后经过的中点进入电场,接着从点射出电场区域内的匀强电场的方向由________(选填“指向”或“指向”),粒子在通过点和点的动能之比为________。
三、解答题
20.如图所示,水平导轨间距为L=0.5m,导轨电阻忽略不计。导体棒ab垂直导轨放置,质量m=1kg,电阻R0=0.9Ω,与导轨接触良好。电源电动势E=10V,内阻r=0.1Ω,电阻R=4Ω。外加匀强磁场的磁感应强度B=5T,方向垂直于ab,与导轨平面成α=53°。ab与导轨间动摩擦因数为μ=0.5(设最大静摩擦力等于滑动摩擦力),不计其余摩擦。重力加速度g=10m/s2,ab处于静止状态。已知sin53°=0.8,cos53°=0.6。求:
(1)ab受到的安培力大小;
(2)如果电阻R的值可以调节,则当R阻值为多少时棒ab刚好要运动。
21.如图所示,在坐标系的第一象限内,直线的上方有垂直纸面向外的有界匀强磁场,磁感应强度大小为;第四象限内,在处有一足够长的光屏与轴垂直放置,光屏与轴之间存在方向沿轴正方向的匀强电场,电场强度大小为;在轴上点处有一粒子源,能以不同速率沿与轴正方向成角发射质量为、电荷量为的相同粒子,这些粒子经磁场作用后都沿轴负方向通过轴,且速度最大的粒子刚好通过直线与轴的交点,速度最小的粒子通过轴上的点(未画出)。已知速度最大的粒子通过轴前一直在磁场中运动,,不计粒子的重力和粒子间的相互作用。,。求:
(1)粒子最大速度的值;
(2)有界磁场的最小面积;
(3)粒子到达光屏上的落点到轴的最大距离。
22.如图所示,在第I象限内的虚线OC(OC与y轴正方向的夹角)与y轴所夹区域内(包括虚线OC)有磁感应强度大小为B、方向垂直于xOy平面向外的匀强磁场,大量质量为m、电荷量为q的带正电粒子(视为质点)从y轴上坐标为(0,L)的A点平行于x轴正方向射入磁场。取,不计粒子所受重力。
(1)若a粒子垂直y轴离开磁场,求其初速度大小v应满足的条件;
(2)若b粒子离开磁场后垂直经过x轴,求b粒子在第I象限内运动的时间t;
(3)若在(2)中情况下,在xOy平面内x轴与虚线OC所夹区域加上方向平行OC的匀强电场(图中未画出)结果b粒子恰好能到达x轴,求所加电场的电场强度大小E以及b粒子到达x轴上的位置的横坐标(不考虑b粒子到达x轴后的运动)。
23.如图(a)所示,两个平行的金属板间接有图(b)所示的交变电压,板长为L=0.4m,板间距d=0.2m。在金属板的右侧即磁场的理想左边界,磁场区域足够大。磁感应强度B=5×10﹣3T,方向垂直纸面向里,现有一带电粒子(不计重力)以v0=105m/s速度沿着极板中线从左端射入极板间。已知粒子的荷质比为 =108C/kg,粒子通过电场区域的极短时间内,可以认为电场是恒定的。
(1)若粒子在t=0时刻射入,求粒子在磁场中运动的射入点到出射点间的距离;
(2)证明任意时刻射入电场的粒子,在磁场中运动的射入点与出射点间的距离都相等;
(3)求粒子射出电场时的最大速度。
24.如图所示,在xoy平面第一象限的整个区域分布向下匀强电场,电场方向平行于y轴向下,在第四象限内存在有界(含边界)匀强磁场,其左边界为y轴,右边界为x=l的直线,磁场方向垂直纸面向外,一质量为m、电荷量为q、可看作质点的带正电粒子,从y轴上P点以初速度v0垂直于y轴射入匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场,已知OQ=l,不计粒子重力,求:
(1)OP间的距离;
(2)要使粒子能再进入电场,磁感应强度B的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度B的取值范围。(结果用m、q、l、v0表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
带电粒子经电压U加速,由动能定理得
qU=mv2
垂直进入磁感应强度为B的匀强磁感中,洛伦兹力提供向心力,
qvB=m
而
R=
联立解得
x=
B、m、q一定,根据数学知识可知,图象是抛物线,由此可知能够正确反应x与U之间的函数关系的是图象B,ACD错误,B正确。
故选B。
2.C
【解析】
【详解】
画出粒子在磁场中运动的轨迹示意图,磁场的边长为L,设粒子的轨道半径为r,由几何关系得
L+rL
解得
r=(1)L
由洛伦兹力提供向心力得
qvB=m
联立解得
故ABD错误C正确。
故选C。
3.C
【解析】
【详解】
由题意知,当电流方向为反向时左边需要再加质量m的砝码后,天平才能平衡,由此可知,电流反向,安培力由向上改为向下,所以磁场方向垂直纸面向外。设矩形线圈的重力为G0,第一次平衡时,左边盘中砝码的质量为m1,右边砝码质量为m2,有
电流反向后,达到平衡时,有
由上述两式可得
故选C。
4.A
【解析】
【分析】
【详解】
电子垂直OM进入磁场后,经半个周期从O点右侧离开磁场,由左手定则可知,磁场方向垂直纸面向里,由周期公式可知
t0==
当电子向左上方垂直射入磁场时,由几何关系可知电子在磁场中运动的轨迹圆弧所对的圆心角为
θ=π
故其在磁场中的运动时间
t=T==t0
故选A。
5.D
【解析】
【详解】
线框下边受到的安培力的大小为
方向向上,线框上边受到的安培力大小
方向向下,根据牛顿第二定律可得
解得
故选D。
6.B
【解析】
【详解】
若电子从a点射出
解得
若电子从d点射出
解得
7.D
【解析】
【详解】
由公式
r =
得带电粒子在匀强磁场中运动的半径r = 0.3m,从Od边射入的粒子,出射点分布在ab和be边;从aO边射入的粒子,出射点分布在ab边和be边。
故选D。
【名师点睛】
抓住粒子运动轨迹然后通过由上向下平移,从而找出交点即出射点。
8.C
【解析】
【详解】
这束正离子束在区域Ⅰ中不偏转,则
qvB1=qE
可知这束正离子的速度相同;进入磁场后半径为
因半径相同,可知离子的荷质比相同。
故选C。
9.C
【解析】
【详解】
根据
F=BLI
可知F-I图像为过原点的直线。
故选C。
10.B
【解析】
【详解】
A.粒子受到的洛伦兹力充当向心力,粒子运动的轨迹半径R=d,粒子运动到绝缘板的两种临界情况如图甲所示
由几何关系可知,左侧最远处与S之间的距离恰好是圆的直径,则左侧最远处A到C距离为d,右侧离C最远处为B,距离为d,所以粒子能打在板上的区域长度是(+1)d,故A错误;
B.左侧最远处与S之间的距离恰好是圆的直径,所以从S到A的时间恰好是半个周期,则
t1===
故B正确;
CD.在磁场中运动时间最长和最短的粒子运动轨迹示意图如图乙所示,粒子做整个圆周运动的周期
T=
由几何关系可知,最短时间
t2=T=
最长时间
t1=T=
Δt=t1-t2=
故CD错误。
故选B。
11.B
【解析】
【详解】
AB.如图所示,利用左手定则画出初末位置的洛伦兹力的方向,由此判断出圆心的所在位置
根据几何关系可得
所以
圆心的坐标为,故A错误B正确;
C.在磁场中,由牛顿第二定律,即
质子射入速度大小为
故C错误;
D.质子在磁场中运动的的周期
质子在磁场中运动的时间
故D错误。
故选B。
12.B
【解析】
【详解】
AB.根据麦克斯韦电磁场理论可知,磁感应强度随时间线性增大时将产生稳定的感应电场,根据楞次定律可知感应电场的方向与小球初速度方向相同,因小球带正电,故电场力对小球做正功,小球的速度逐渐增大,向心力的大小随之增大,故A错误,B正确;
C.洛伦兹力对小球不做功,故C错误;
D.带电小球所受的洛伦兹力为
因为速率v随时间逐渐增大,且磁感应强度B的大小跟时间成正比,所以小球受到的洛伦兹力大小与时间不成正比,故D错误。
故选B。
13.A
【解析】
【详解】
ABD.由圆的性质可知,轨迹圆与磁场圆相交,当轨迹圆的弦长最大时偏转角最大,故应该使弦长为PQ,由Q点飞出的离子圆心角最大,所对应的时间最长,轨迹不可能经过圆心O点,故A正确,BD错误;
C.因洛伦兹力永不做功,故粒子在磁场中运动时动能保持不变,但由于离子的初动能不一定相等,故飞出时的动能不一定相等,故C错误。
故选A。
14.C
【解析】
【详解】
A.根据
解得
故粒子加速后的最大速度与D型金属盒的半径有关,故A错误;
B.根据
联立解得
最大动能与半径和磁感应强度有关与加速电压无关,故B错误;
CD.根据
可知高频电源频率由粒子的质量、电量和磁感应强度决定,故C正确,D错误。
故选C。
15.B
【解析】
【详解】
由洛伦兹力提供向心力可得
v=
所以粒子在磁场中运动的半径为
r==L
粒子在磁场中运动时间最短,对应的弧长最短、弦长最短,由几何关系得,当弦长等于L时最短,此时弦切角为30°,圆心角为60°,如图所示,运动的最短时间是
tmin=T=×=
ACD错误,故B正确。
故选B。
16.
【解析】
【分析】
【详解】
[1]墨滴在电场区域做匀速直线运动,有
解得
由于电场方向向上,电荷所受电场力向上,可知墨滴带负电荷。
[2]墨滴垂直进入电场、磁场共存区域,重力仍与电场力平衡,合力等于洛伦兹力,墨滴做匀速圆周运动,有
墨滴在磁场区域恰完成四分之一圆周运动,则半径为
联立解得
17. 磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同
【解析】
【详解】
(1)[1]导线受安培力的大小为
长L的导线内的总的带电粒子数为
又
电荷定向运动时所受洛伦兹力的矢量和,变现为导线所受的安培力,即
联立可以推导出洛伦兹力的表达式为
(2)[2][3]用洛伦兹力来定义磁感应强度,定义式为
两个定义式(而非物理量)的差别在于:磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同。
18. 相同
【解析】
【分析】
【详解】
[1] a棒静止,传感器受到a给它水平向左、大小为F的拉力,说明两导体棒互相吸引,则a、b中的电流方向相同;
[2] a中电流在b棒所在处产生的磁感应强度大小为
19. c指向b 5:1
【解析】
【详解】
[1]根据粒子在磁场中受洛伦兹力而从d点进e点出,由左手定则知带正电,根据磁场中运动的对称性知e点的速度大小等于v0,方向与bd成45°,即竖直向下,而在电场中做类平抛运动,可知粒子受的电场力由c指向b,则电场方向由c指向b;
[2]粒子从d到e做匀速圆周运动,速度的大小不变,而e到b做类平抛运动,水平位移等于竖直位移
2vxt=v0t
则到达b点的水平速度
合速度为
则粒子在b点和d点的动能之比为
20.(1);(2)
【解析】
【详解】
(1)根据闭合电路欧姆定律,可得
由安培力表达式,有
(2)对ab棒受力分析,如图
棒ab刚好要运动,有
又
联立,可得
由安培力表达式与闭合电路欧姆定律可得
解得
当R阻值为时棒ab刚好要运动。
21.(1);(2) ;(3)
【解析】
【详解】
(1)设粒子的最大速度为,由于速度最大的粒子穿过x轴前一直在磁场内运动,过P点作速度的垂线交x轴于O1点,就是速度为的粒子做圆周运动的圆心,PO1即为半径R1,如图1
由几何关系有
解得
由洛伦兹力提供向心力,则
解得
(2)设速度最小的粒子在磁场中半径为R2,速度为,根据几何关系有
解得
,
磁场的最小面积为图1中PCM阴影部分面积
解得
(3)设某个粒子轨迹与直线交点为C1,到达x轴上点N1时,距离原点O的距离为x,如图2
该粒子对应的速度为v,轨迹半径为R,由几何关系得
解得
又由
解得
该粒子在电场中运动时间为t,有
解得
粒子打到光屏上的位置距离x轴的距离为Y,有
其中
当时,有最大距离
22.(1);(2);(3);
【解析】
【详解】
(1)当a粒子在磁场中的运动轨迹对应的圆心角为180°时,a粒子垂直y轴离开磁场,在此种情况下,当a粒子的运动轨迹与OC相切时,a粒子的初速度最大(设为),如图甲所示。
设此时a粒子在磁场中运动的轨迹半径为,有
根据几何关系有
解得
v应满足的条件为
(2)b粒子运动四分之一圆周后离开磁场,将垂直经过x轴,运动轨迹如图乙所示
设轨迹圆的半径为,有
根据几何关系有
解得
b点粒子在磁场中做圆周运动的周期
b粒子在磁场中运动的时间
解得
根据几何关系,b粒子经过虚线OC时到x轴的距离
设b粒子离开磁场后在第I象限内运动的时间为,有
又
解得
(3)b粒子沿y轴方向的加速度大小
根据匀变速直线运动的规律有
解得
b粒子沿x轴方向的加速度大小
设b粒子从虚线OC运动到x轴的时间为,有
b粒子从虚线OC运动到x轴的过程中沿x轴方向的位移大小
又
解得
23.(1)0.4m;(2)见解析;(3)
【解析】
【详解】
(1)带电粒子在t=0时刻进入,由题可知,粒子通过电场区域时间极短,因此粒子从进入电场到离开电场,板间电场强度始终为零,则粒子将以v0的速度垂直磁场左边界射入磁场中,由牛顿第二定律,得
得
r==0.2m
故粒子在磁场中运动的射入点到出射点间的距离
s=2r=0.4m
(2)设某时刻进入磁场的粒子速度为v,方向与水平方向成θ角,
则
v=
粒子在磁场中运动时的轨迹半径为
==
粒子射入点到出射点间的距离为
s′=2r′cosθ=2
由(1)知
s′=2r=0.4m
故任意时刻射入电场的粒子,在磁场中运动的射入点与出射点间的距离都相等.
(3)设粒子进入电场时刻,板间的电压为U,且粒子可以射出电场进入磁场.则
y=
t=
当侧移量y=时,电场力对粒子做功最多, 解得
U=
代入解得
U=25V
由动能定理得
q=﹣
解得
vm=
24.(1)l;(2)B≥;(3)≤B≤
【解析】
【详解】
(1)设粒子进入电场时y方向的速度为vy,则
vy=v0tan45°
设粒子在电场中运动时间为t,则
OQ=l=v0t
OP=t
联立解得
OP=l
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则
r1+r1sin45°=l
解得
r1=(2﹣)l
令粒子在磁场中的速度为v,则
v=
根据牛顿第二定律
qvB1=m
解得
B1=
要使粒子能再进入电场,磁感应强度B的范围为
B≥B1=
(3)假设粒子刚好从x=l处磁场边界与电场的交界D处第二次进入磁场,设粒子从P到Q的时间为t,则由粒子在电场中运动对称性可知粒子从第一次出磁场的C点到D的时间为2t,由水平方向的匀速直线运动可得
CD=2d
CQ=CD﹣QD=2d﹣(2.5d﹣d)=l
设此时粒子在磁场中的轨道半径为r2,由几何关系知
2r2sin45°=CQ
解得
r2=l
根据牛顿第二定律得
qvB2=m
解得
B2=
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足
B≤B2=
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
≤B≤
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图所示,一个静止的质量为m、带电荷量为q的粒子(不计重力),经电压U加速后垂直进入磁感应强度为B的匀强磁感中,粒子打至P点。设OP=x,能够正确反应x与U之间的函数关系的图象是( )
A. B.
C. D.
2.如图所示,abcd为边长为L的正方形,在四分之一圆abd区域内有垂直正方形平面向外的匀强磁场,磁场的磁感应强度为B。一个质量为m、电荷量为q的带电粒子从b点沿ba方向射入磁场,结果粒子恰好能通过c点,且射出磁场时的速度反向延长线通过a点,不计粒子的重力,则粒子的速度大小为( )
A. B. C. D.
3.如图所示装置,天平可以用来测定磁感应强度B的大小和方向,天平的右臂下面挂有一个共N匝的矩形线圈,线圈宽为l。线圈的下部悬在匀强磁场中,磁场方向垂直于纸面,线圈中通有如图所示方向的电流I时,在天平左、右两边加上质量分别为m1、m2的砝码,天平平衡;当只改变电流的方向时,需要在天平左边再加上质量为m的砝码后,天平才重新达到平衡。那么( )
A.B的方向垂直纸面向外,大小为
B.B的方向垂直纸面向里,大小为
C.B的方向垂直纸面向外,大小为
D.B的方向垂直纸面向里,大小为
4.图所示,直线OM上方存在着垂直纸面方向的匀强磁场(未画出),一电子从O点垂直OM射入磁场,经过时间t0从O点右侧某位置射出磁场.现使电子从O点向左上方射入磁场,速度方向与OM成150°角,则( )
A.磁场方向垂直纸面向里,电子在磁场中经历的时间为 t0
B.磁场方向垂直纸面向外,电子在磁场中经历的时间为t0
C.磁场方向垂直纸面向里,电子在磁场中经历的时间为 t0
D.磁场方向垂直纸面向外,电子在磁场中经历的时间为t0
5.如图所示,无限长水平直导线中通有向右的恒定电流I,导线正上方沿竖直方向有一绝缘细线悬挂着的正方形线框。线框中通有沿逆时针方向的恒定电流I,线框的边长为L,线框下边与直导线平行,且到直导线的距离也为L。已知在长直导线的磁场中距长直导线r处的磁感应强度大小为(k为常量),线框的质量为m,则剪断细线的瞬间,线框的加速度为( )
A.0 B. C. D.
6.如图,边长为l的正方形abcd内存在均匀磁场,磁感应度大小为B,方向垂直于纸面(abcd所在平面)向外。ab边中点有一电子发射源O,可向磁场内沿垂直于ab边的方向发射电子。已知电子的比荷为k,则从a、d两点射出的电子的速度大小分别为( )
A., B.,
C., D.,
7.如图所示,长方形abcd长ad = 0.6m,宽ab = 0.3m,O、e分别是ad、bc的中点,以ad为直径的半圆内有垂直纸面向里的匀强磁场(边界上无磁场),磁感应强度B = 0.25T。一群不计重力、质量m = 3 × 10 - 7kg、电荷量q = + 2 × 10 - 3C的带电粒子以速度v = 5 × 102m/s沿垂直ad方向且垂直于磁场射入磁场区域,则( )
A.从Od边射入的粒子,出射点全部分布在Oa边
B.从aO边射入的粒子,出射点全部分布在ab边
C.从Od边射入的粒子,出射点分布在Oa边和ab边
D.从aO边射入的粒子,出射点分布在ab边和bc边
8.如图所示,有一混合正离子束先后通过正交电场磁场区域Ⅰ和匀强磁场区域Ⅱ,如果这束正离子束在区域Ⅰ中不偏转,进入区域Ⅱ后偏转半径又相同,则说明这些正离子具有相同的( )
A.质量 B.动能 C.荷质比 D.电荷
9.在恒定的匀强磁场中固定一根通电直导线,导线的方向与磁场方向垂直,如图反映的是这根导线受到的磁场力大小F与通过导线的电流I之间的关系,M、N两点各对应一组F、I的数据,其中可能正确的是( )
A. B. C. D.
10.如图所示,在绝缘板MN上方分布了水平方向的匀强磁场,方向垂直于纸面向里。距离绝缘板d处有一粒子源S,能够在纸面内不断地向各个方向同时发射电荷量为q、质量为m、速率为v的带正电粒子,不计粒子的重力和粒子间的相互作用,已知粒子做圆周运动的半径也恰好为d,则( )
A.粒子能打到板上的区域长度为2d
B.能打到板上最左侧的粒子所用的时间为
C.粒子从发射到打到板上的最长时间为
D.同一时刻发射的粒子打到板上的最大时间差为
11.如图所示,在第一象限内存在着垂直纸面向里的匀强磁场。一质子从P点垂直磁场射入,射入时速度方向与x轴夹角为60°,质子从y轴上离开磁场时速度方向与y轴垂直。已知质子电荷量为e、质量为m,磁场磁感应强度大小为B,P点的坐标为,则( )
A.质子在磁场中运动的轨迹圆的圆心的坐标为
B.质子在磁场中运动的轨迹圆的半径
C.质子射入速度大小为
D.质子在磁场中运动的时间为
12.如图所示是一个水平放置的圆环形玻璃小槽,槽内光滑,槽宽度和深度处处相同.现将一直径略小于槽宽的带正电小球放在槽中,让它受绝缘棒打击后获得一初速度v0.与此同时,有一变化的磁场垂直穿过圆环形玻璃小槽外径所对应的圆面积,磁感应强度B的大小跟时间成正比,方向竖直向下.设小球在运动过程中所带电荷量不变,那么( )
A.小球受到的向心力大小不变
B.小球受到的向心力大小不断增加
C.洛伦兹力对小球做功
D.小球受到的洛伦兹力大小与时间成正比
13.如图所示,在半径为R的圆形区域内(圆心为O)有匀强磁场,磁感应强度为B,方向垂直于圆平面(未画出)。一群具有相同比荷的负离子以相同的速率由P点在纸平面内沿不同方向射入磁场中,发生偏转后又飞出磁场,若离子在磁场中运动的轨道半径大于R,则下列说法中正确的是(不计离子的重力)( )
A.从Q点飞出的离子在磁场中运动的时间最长
B.沿PQ方向射入的离子飞出时偏转角最大
C.所有离子飞出磁场时的动能一定相等
D.在磁场中运动时间最长的离子可能经过圆心O点
14.回旋加速器是用来加速带电粒子使它获得很大动能的装置,其核心部分是两个D型金属盒,置于匀强磁场中,两盒分别与高频电源相连。下列说法正确的是( )
A.粒子被加速后的最大速度与D型金属盒的半径无关
B.粒子被加速后的最大动能随高频电源的加速电压的增大而增大
C.高频电源频率由粒子的质量、电量和磁感应强度决定
D.高频电源频率与粒子的质量、电量和磁感应强度无关
15.如图所示,MN的右侧存在范围足够大、磁感应强度大小为B的匀强磁场,磁场方向垂直纸面向里,MN右侧到MN的距离为L的O处有一个粒子源,可沿纸面内各个方向射出质量为m、电荷量为q的带正电粒子(不计重力及粒子间的相互作用),速度均为,则粒子在磁场中运动的最短时间为( )
A. B. C. D.
二、填空题
16.如图,上下两块金属板水平放置,相距为d,板间电压为U。两板间右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机喷嘴处在两板中线左侧位置,从喷嘴水平向右喷出质量为m、速度为v0的带电墨滴。墨滴在电场区域恰能做匀速直线运动,并垂直磁场左边界进入电场、磁场共存区域,最终垂直打在下板上。重力加速度为g,则墨滴带电量大小q=_______ ; 磁感应强度B=_________(均用题中物理量符号表示)。
17.导体棒中带电粒子的定向移动形成电流,电流可以从宏观和微观两个角度来认识,安培力与洛伦兹力也有宏观与微观的对应关系。
如图所示,静止不动的匀强磁场的磁感应强度大小为B,方向竖直向下。一段直导体棒长为L,横截面积为S,单位体积的自由电荷个数为n,自由电荷的电荷量为。导体棒中通有恒定电流,自由电荷的定向移动速率为(本题中两问均认为始终不变)。导体棒水平放置处于磁场中(垂直于磁感应强度)。
(1)若导体棒相对磁场静止,电荷定向运动时所受洛伦兹力的矢量和,在宏观上表现为导体棒所受的安培力。按照这个思路,请你由安培力的表达式推导出洛伦兹力大小的表达式。( )
(2)概念学习中,类比与比较是常用的学习方法。我们已经知道,垂直于匀强磁场磁感线的通电导线所受的安培力,由此,我们用来定义磁感应强度。同样,运动方向垂直于匀强磁场磁感线的带电粒子所受的洛伦兹力,由此也可用洛伦兹力来定义磁感应强度,定义式是_________,把该定义式与电场强度的定义式进行对比,两个定义式(而非物理量)的差别在于:__________________
18.如图,长度均为L的长直导体棒a、b平行置于光滑绝缘水平桌面,b棒固定,a棒与力传感器相连。当a、b中分别通以大小为Ia、Ib的恒定电流时,a棒静止,传感器受到a给它水平向左、大小为F的拉力。则a、b中的电流方向______(选填“相同”或“相反”),a中电流在b棒所在处产生的磁感应强度大小为______。
19.如图,在正方形中的区域内,存在方向垂直纸面向里的匀强磁场,区域内有方向平行的匀强电场(图中未画出)。现有一带电粒子(不计重力)从点沿方向射入磁场,随后经过的中点进入电场,接着从点射出电场区域内的匀强电场的方向由________(选填“指向”或“指向”),粒子在通过点和点的动能之比为________。
三、解答题
20.如图所示,水平导轨间距为L=0.5m,导轨电阻忽略不计。导体棒ab垂直导轨放置,质量m=1kg,电阻R0=0.9Ω,与导轨接触良好。电源电动势E=10V,内阻r=0.1Ω,电阻R=4Ω。外加匀强磁场的磁感应强度B=5T,方向垂直于ab,与导轨平面成α=53°。ab与导轨间动摩擦因数为μ=0.5(设最大静摩擦力等于滑动摩擦力),不计其余摩擦。重力加速度g=10m/s2,ab处于静止状态。已知sin53°=0.8,cos53°=0.6。求:
(1)ab受到的安培力大小;
(2)如果电阻R的值可以调节,则当R阻值为多少时棒ab刚好要运动。
21.如图所示,在坐标系的第一象限内,直线的上方有垂直纸面向外的有界匀强磁场,磁感应强度大小为;第四象限内,在处有一足够长的光屏与轴垂直放置,光屏与轴之间存在方向沿轴正方向的匀强电场,电场强度大小为;在轴上点处有一粒子源,能以不同速率沿与轴正方向成角发射质量为、电荷量为的相同粒子,这些粒子经磁场作用后都沿轴负方向通过轴,且速度最大的粒子刚好通过直线与轴的交点,速度最小的粒子通过轴上的点(未画出)。已知速度最大的粒子通过轴前一直在磁场中运动,,不计粒子的重力和粒子间的相互作用。,。求:
(1)粒子最大速度的值;
(2)有界磁场的最小面积;
(3)粒子到达光屏上的落点到轴的最大距离。
22.如图所示,在第I象限内的虚线OC(OC与y轴正方向的夹角)与y轴所夹区域内(包括虚线OC)有磁感应强度大小为B、方向垂直于xOy平面向外的匀强磁场,大量质量为m、电荷量为q的带正电粒子(视为质点)从y轴上坐标为(0,L)的A点平行于x轴正方向射入磁场。取,不计粒子所受重力。
(1)若a粒子垂直y轴离开磁场,求其初速度大小v应满足的条件;
(2)若b粒子离开磁场后垂直经过x轴,求b粒子在第I象限内运动的时间t;
(3)若在(2)中情况下,在xOy平面内x轴与虚线OC所夹区域加上方向平行OC的匀强电场(图中未画出)结果b粒子恰好能到达x轴,求所加电场的电场强度大小E以及b粒子到达x轴上的位置的横坐标(不考虑b粒子到达x轴后的运动)。
23.如图(a)所示,两个平行的金属板间接有图(b)所示的交变电压,板长为L=0.4m,板间距d=0.2m。在金属板的右侧即磁场的理想左边界,磁场区域足够大。磁感应强度B=5×10﹣3T,方向垂直纸面向里,现有一带电粒子(不计重力)以v0=105m/s速度沿着极板中线从左端射入极板间。已知粒子的荷质比为 =108C/kg,粒子通过电场区域的极短时间内,可以认为电场是恒定的。
(1)若粒子在t=0时刻射入,求粒子在磁场中运动的射入点到出射点间的距离;
(2)证明任意时刻射入电场的粒子,在磁场中运动的射入点与出射点间的距离都相等;
(3)求粒子射出电场时的最大速度。
24.如图所示,在xoy平面第一象限的整个区域分布向下匀强电场,电场方向平行于y轴向下,在第四象限内存在有界(含边界)匀强磁场,其左边界为y轴,右边界为x=l的直线,磁场方向垂直纸面向外,一质量为m、电荷量为q、可看作质点的带正电粒子,从y轴上P点以初速度v0垂直于y轴射入匀强电场,在电场力作用下从x轴上Q点以与x轴正方向成45°角进入匀强磁场,已知OQ=l,不计粒子重力,求:
(1)OP间的距离;
(2)要使粒子能再进入电场,磁感应强度B的取值范围;
(3)要使粒子能第二次进入磁场,磁感应强度B的取值范围。(结果用m、q、l、v0表示)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【详解】
带电粒子经电压U加速,由动能定理得
qU=mv2
垂直进入磁感应强度为B的匀强磁感中,洛伦兹力提供向心力,
qvB=m
而
R=
联立解得
x=
B、m、q一定,根据数学知识可知,图象是抛物线,由此可知能够正确反应x与U之间的函数关系的是图象B,ACD错误,B正确。
故选B。
2.C
【解析】
【详解】
画出粒子在磁场中运动的轨迹示意图,磁场的边长为L,设粒子的轨道半径为r,由几何关系得
L+rL
解得
r=(1)L
由洛伦兹力提供向心力得
qvB=m
联立解得
故ABD错误C正确。
故选C。
3.C
【解析】
【详解】
由题意知,当电流方向为反向时左边需要再加质量m的砝码后,天平才能平衡,由此可知,电流反向,安培力由向上改为向下,所以磁场方向垂直纸面向外。设矩形线圈的重力为G0,第一次平衡时,左边盘中砝码的质量为m1,右边砝码质量为m2,有
电流反向后,达到平衡时,有
由上述两式可得
故选C。
4.A
【解析】
【分析】
【详解】
电子垂直OM进入磁场后,经半个周期从O点右侧离开磁场,由左手定则可知,磁场方向垂直纸面向里,由周期公式可知
t0==
当电子向左上方垂直射入磁场时,由几何关系可知电子在磁场中运动的轨迹圆弧所对的圆心角为
θ=π
故其在磁场中的运动时间
t=T==t0
故选A。
5.D
【解析】
【详解】
线框下边受到的安培力的大小为
方向向上,线框上边受到的安培力大小
方向向下,根据牛顿第二定律可得
解得
故选D。
6.B
【解析】
【详解】
若电子从a点射出
解得
若电子从d点射出
解得
7.D
【解析】
【详解】
由公式
r =
得带电粒子在匀强磁场中运动的半径r = 0.3m,从Od边射入的粒子,出射点分布在ab和be边;从aO边射入的粒子,出射点分布在ab边和be边。
故选D。
【名师点睛】
抓住粒子运动轨迹然后通过由上向下平移,从而找出交点即出射点。
8.C
【解析】
【详解】
这束正离子束在区域Ⅰ中不偏转,则
qvB1=qE
可知这束正离子的速度相同;进入磁场后半径为
因半径相同,可知离子的荷质比相同。
故选C。
9.C
【解析】
【详解】
根据
F=BLI
可知F-I图像为过原点的直线。
故选C。
10.B
【解析】
【详解】
A.粒子受到的洛伦兹力充当向心力,粒子运动的轨迹半径R=d,粒子运动到绝缘板的两种临界情况如图甲所示
由几何关系可知,左侧最远处与S之间的距离恰好是圆的直径,则左侧最远处A到C距离为d,右侧离C最远处为B,距离为d,所以粒子能打在板上的区域长度是(+1)d,故A错误;
B.左侧最远处与S之间的距离恰好是圆的直径,所以从S到A的时间恰好是半个周期,则
t1===
故B正确;
CD.在磁场中运动时间最长和最短的粒子运动轨迹示意图如图乙所示,粒子做整个圆周运动的周期
T=
由几何关系可知,最短时间
t2=T=
最长时间
t1=T=
Δt=t1-t2=
故CD错误。
故选B。
11.B
【解析】
【详解】
AB.如图所示,利用左手定则画出初末位置的洛伦兹力的方向,由此判断出圆心的所在位置
根据几何关系可得
所以
圆心的坐标为,故A错误B正确;
C.在磁场中,由牛顿第二定律,即
质子射入速度大小为
故C错误;
D.质子在磁场中运动的的周期
质子在磁场中运动的时间
故D错误。
故选B。
12.B
【解析】
【详解】
AB.根据麦克斯韦电磁场理论可知,磁感应强度随时间线性增大时将产生稳定的感应电场,根据楞次定律可知感应电场的方向与小球初速度方向相同,因小球带正电,故电场力对小球做正功,小球的速度逐渐增大,向心力的大小随之增大,故A错误,B正确;
C.洛伦兹力对小球不做功,故C错误;
D.带电小球所受的洛伦兹力为
因为速率v随时间逐渐增大,且磁感应强度B的大小跟时间成正比,所以小球受到的洛伦兹力大小与时间不成正比,故D错误。
故选B。
13.A
【解析】
【详解】
ABD.由圆的性质可知,轨迹圆与磁场圆相交,当轨迹圆的弦长最大时偏转角最大,故应该使弦长为PQ,由Q点飞出的离子圆心角最大,所对应的时间最长,轨迹不可能经过圆心O点,故A正确,BD错误;
C.因洛伦兹力永不做功,故粒子在磁场中运动时动能保持不变,但由于离子的初动能不一定相等,故飞出时的动能不一定相等,故C错误。
故选A。
14.C
【解析】
【详解】
A.根据
解得
故粒子加速后的最大速度与D型金属盒的半径有关,故A错误;
B.根据
联立解得
最大动能与半径和磁感应强度有关与加速电压无关,故B错误;
CD.根据
可知高频电源频率由粒子的质量、电量和磁感应强度决定,故C正确,D错误。
故选C。
15.B
【解析】
【详解】
由洛伦兹力提供向心力可得
v=
所以粒子在磁场中运动的半径为
r==L
粒子在磁场中运动时间最短,对应的弧长最短、弦长最短,由几何关系得,当弦长等于L时最短,此时弦切角为30°,圆心角为60°,如图所示,运动的最短时间是
tmin=T=×=
ACD错误,故B正确。
故选B。
16.
【解析】
【分析】
【详解】
[1]墨滴在电场区域做匀速直线运动,有
解得
由于电场方向向上,电荷所受电场力向上,可知墨滴带负电荷。
[2]墨滴垂直进入电场、磁场共存区域,重力仍与电场力平衡,合力等于洛伦兹力,墨滴做匀速圆周运动,有
墨滴在磁场区域恰完成四分之一圆周运动,则半径为
联立解得
17. 磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同
【解析】
【详解】
(1)[1]导线受安培力的大小为
长L的导线内的总的带电粒子数为
又
电荷定向运动时所受洛伦兹力的矢量和,变现为导线所受的安培力,即
联立可以推导出洛伦兹力的表达式为
(2)[2][3]用洛伦兹力来定义磁感应强度,定义式为
两个定义式(而非物理量)的差别在于:磁感应强度是描述磁场力的性质的物理量,它的方向是小磁针静止时N极的受力方向;电场强度是描述电场力的性质的物理量,它的方向与正电荷的受力方向相同。
18. 相同
【解析】
【分析】
【详解】
[1] a棒静止,传感器受到a给它水平向左、大小为F的拉力,说明两导体棒互相吸引,则a、b中的电流方向相同;
[2] a中电流在b棒所在处产生的磁感应强度大小为
19. c指向b 5:1
【解析】
【详解】
[1]根据粒子在磁场中受洛伦兹力而从d点进e点出,由左手定则知带正电,根据磁场中运动的对称性知e点的速度大小等于v0,方向与bd成45°,即竖直向下,而在电场中做类平抛运动,可知粒子受的电场力由c指向b,则电场方向由c指向b;
[2]粒子从d到e做匀速圆周运动,速度的大小不变,而e到b做类平抛运动,水平位移等于竖直位移
2vxt=v0t
则到达b点的水平速度
合速度为
则粒子在b点和d点的动能之比为
20.(1);(2)
【解析】
【详解】
(1)根据闭合电路欧姆定律,可得
由安培力表达式,有
(2)对ab棒受力分析,如图
棒ab刚好要运动,有
又
联立,可得
由安培力表达式与闭合电路欧姆定律可得
解得
当R阻值为时棒ab刚好要运动。
21.(1);(2) ;(3)
【解析】
【详解】
(1)设粒子的最大速度为,由于速度最大的粒子穿过x轴前一直在磁场内运动,过P点作速度的垂线交x轴于O1点,就是速度为的粒子做圆周运动的圆心,PO1即为半径R1,如图1
由几何关系有
解得
由洛伦兹力提供向心力,则
解得
(2)设速度最小的粒子在磁场中半径为R2,速度为,根据几何关系有
解得
,
磁场的最小面积为图1中PCM阴影部分面积
解得
(3)设某个粒子轨迹与直线交点为C1,到达x轴上点N1时,距离原点O的距离为x,如图2
该粒子对应的速度为v,轨迹半径为R,由几何关系得
解得
又由
解得
该粒子在电场中运动时间为t,有
解得
粒子打到光屏上的位置距离x轴的距离为Y,有
其中
当时,有最大距离
22.(1);(2);(3);
【解析】
【详解】
(1)当a粒子在磁场中的运动轨迹对应的圆心角为180°时,a粒子垂直y轴离开磁场,在此种情况下,当a粒子的运动轨迹与OC相切时,a粒子的初速度最大(设为),如图甲所示。
设此时a粒子在磁场中运动的轨迹半径为,有
根据几何关系有
解得
v应满足的条件为
(2)b粒子运动四分之一圆周后离开磁场,将垂直经过x轴,运动轨迹如图乙所示
设轨迹圆的半径为,有
根据几何关系有
解得
b点粒子在磁场中做圆周运动的周期
b粒子在磁场中运动的时间
解得
根据几何关系,b粒子经过虚线OC时到x轴的距离
设b粒子离开磁场后在第I象限内运动的时间为,有
又
解得
(3)b粒子沿y轴方向的加速度大小
根据匀变速直线运动的规律有
解得
b粒子沿x轴方向的加速度大小
设b粒子从虚线OC运动到x轴的时间为,有
b粒子从虚线OC运动到x轴的过程中沿x轴方向的位移大小
又
解得
23.(1)0.4m;(2)见解析;(3)
【解析】
【详解】
(1)带电粒子在t=0时刻进入,由题可知,粒子通过电场区域时间极短,因此粒子从进入电场到离开电场,板间电场强度始终为零,则粒子将以v0的速度垂直磁场左边界射入磁场中,由牛顿第二定律,得
得
r==0.2m
故粒子在磁场中运动的射入点到出射点间的距离
s=2r=0.4m
(2)设某时刻进入磁场的粒子速度为v,方向与水平方向成θ角,
则
v=
粒子在磁场中运动时的轨迹半径为
==
粒子射入点到出射点间的距离为
s′=2r′cosθ=2
由(1)知
s′=2r=0.4m
故任意时刻射入电场的粒子,在磁场中运动的射入点与出射点间的距离都相等.
(3)设粒子进入电场时刻,板间的电压为U,且粒子可以射出电场进入磁场.则
y=
t=
当侧移量y=时,电场力对粒子做功最多, 解得
U=
代入解得
U=25V
由动能定理得
q=﹣
解得
vm=
24.(1)l;(2)B≥;(3)≤B≤
【解析】
【详解】
(1)设粒子进入电场时y方向的速度为vy,则
vy=v0tan45°
设粒子在电场中运动时间为t,则
OQ=l=v0t
OP=t
联立解得
OP=l
(2)粒子刚好能再进入电场的轨迹如图所示,设此时的轨迹半径为r1,则
r1+r1sin45°=l
解得
r1=(2﹣)l
令粒子在磁场中的速度为v,则
v=
根据牛顿第二定律
qvB1=m
解得
B1=
要使粒子能再进入电场,磁感应强度B的范围为
B≥B1=
(3)假设粒子刚好从x=l处磁场边界与电场的交界D处第二次进入磁场,设粒子从P到Q的时间为t,则由粒子在电场中运动对称性可知粒子从第一次出磁场的C点到D的时间为2t,由水平方向的匀速直线运动可得
CD=2d
CQ=CD﹣QD=2d﹣(2.5d﹣d)=l
设此时粒子在磁场中的轨道半径为r2,由几何关系知
2r2sin45°=CQ
解得
r2=l
根据牛顿第二定律得
qvB2=m
解得
B2=
要使粒子能第二次进磁场,粒子必须先进入电场,故磁感应强度B要满足
B≤B2=
综上所述要使粒子能第二次进磁场,磁感应强度B要满足
≤B≤
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 磁场
- 第一节 安培力
- 第二节 安培力的应用
- 第三节 洛伦兹力
- 第四节 洛伦兹力与现代技术
- 第二章 电磁感应
- 第一节 感应电流的方向
- 第二节 法拉第电磁感应定律
- 第三节 电磁感应定律的应用
- 第四节 互感和自感
- 第五节 涡流现象及其应用
- 第三章 交变电流
- 第一节 认识交变电流
- 第二节 描述交变电流的物理量
- 第三节 变压器
- 第四节 远距离输电
- 第四章 电磁震荡与电磁波
- 第一节 电磁振动
- 第二节 麦克斯韦电磁电磁场理论
- 第三节 电磁波的发射、传播和接收
- 第四节 电磁波谱
- 第五章 传感器
- 第一节 传感器及其工作原理
- 第二节 传感器的应用
- 第三节 用传感器制作自动控制装置
- 第四节 利用智能手机中的磁传感器研究磁现象
