8.3.1 棱柱、棱锥、棱台的表面积和体积练习题(word含解析)
文档属性
| 名称 | 8.3.1 棱柱、棱锥、棱台的表面积和体积练习题(word含解析) | 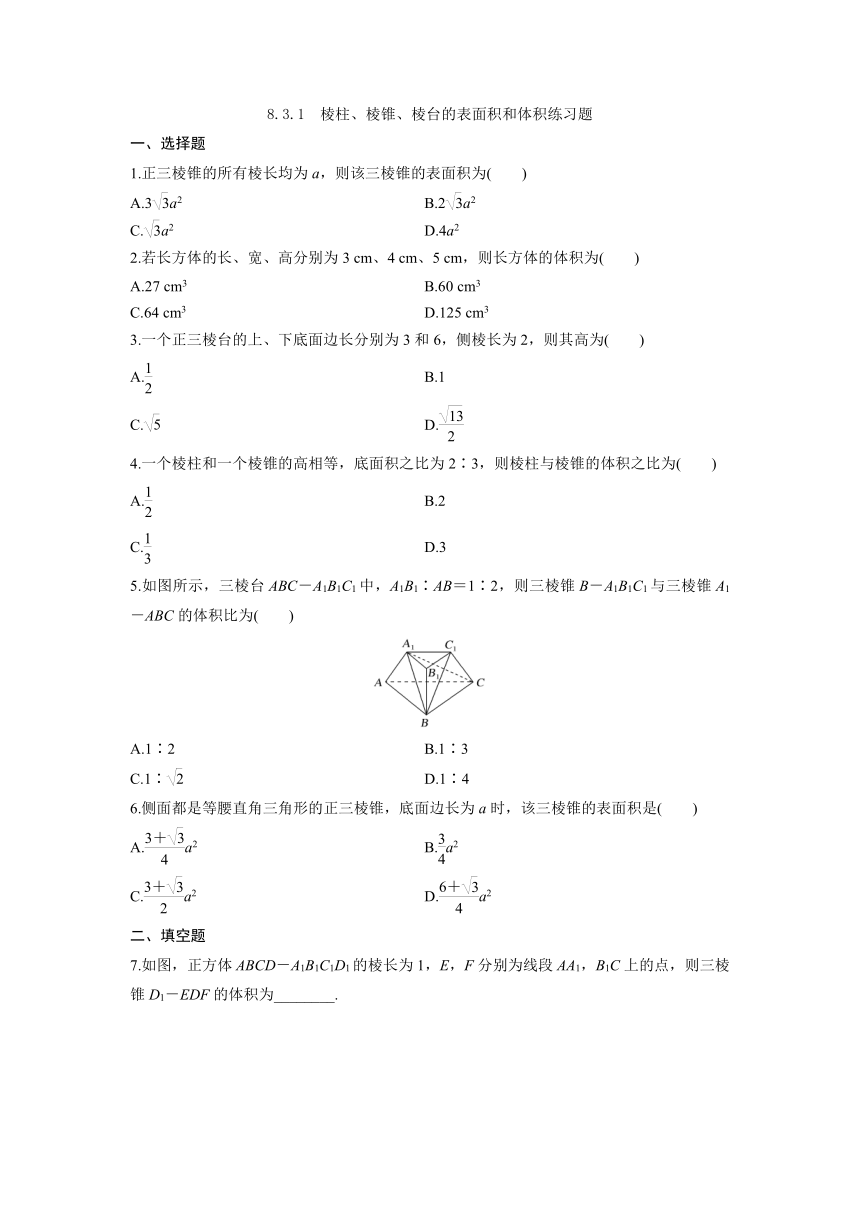 | |
| 格式 | docx | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 15:58:30 | ||
图片预览


文档简介
8.3.1 棱柱、棱锥、棱台的表面积和体积练习题
一、选择题
1.正三棱锥的所有棱长均为a,则该三棱锥的表面积为( )
A.3a2 B.2a2
C.a2 D.4a2
2.若长方体的长、宽、高分别为3 cm、4 cm、5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3
C.64 cm3 D.125 cm3
3.一个正三棱台的上、下底面边长分别为3和6,侧棱长为2,则其高为( )
A. B.1
C. D.
4.一个棱柱和一个棱锥的高相等,底面积之比为2∶3,则棱柱与棱锥的体积之比为( )
A. B.2
C. D.3
5.如图所示,三棱台ABC-A1B1C1中,A1B1∶AB=1∶2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积比为( )
A.1∶2 B.1∶3
C.1∶ D.1∶4
6.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
二、填空题
7.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.
8.一个正四棱台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13 cm,则其表面积为________ cm2.
9.三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则=________.
10.如图所示,已知正四棱锥的侧棱长为4,底面边长为4,则该四棱锥的体积为________.
11.已知正四棱台的高是12 cm,两底面边长之差为10 cm,全面积为512 cm2,则上、下底面边长分别为________cm,体积为________cm3.
三、解答题
12.如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d.
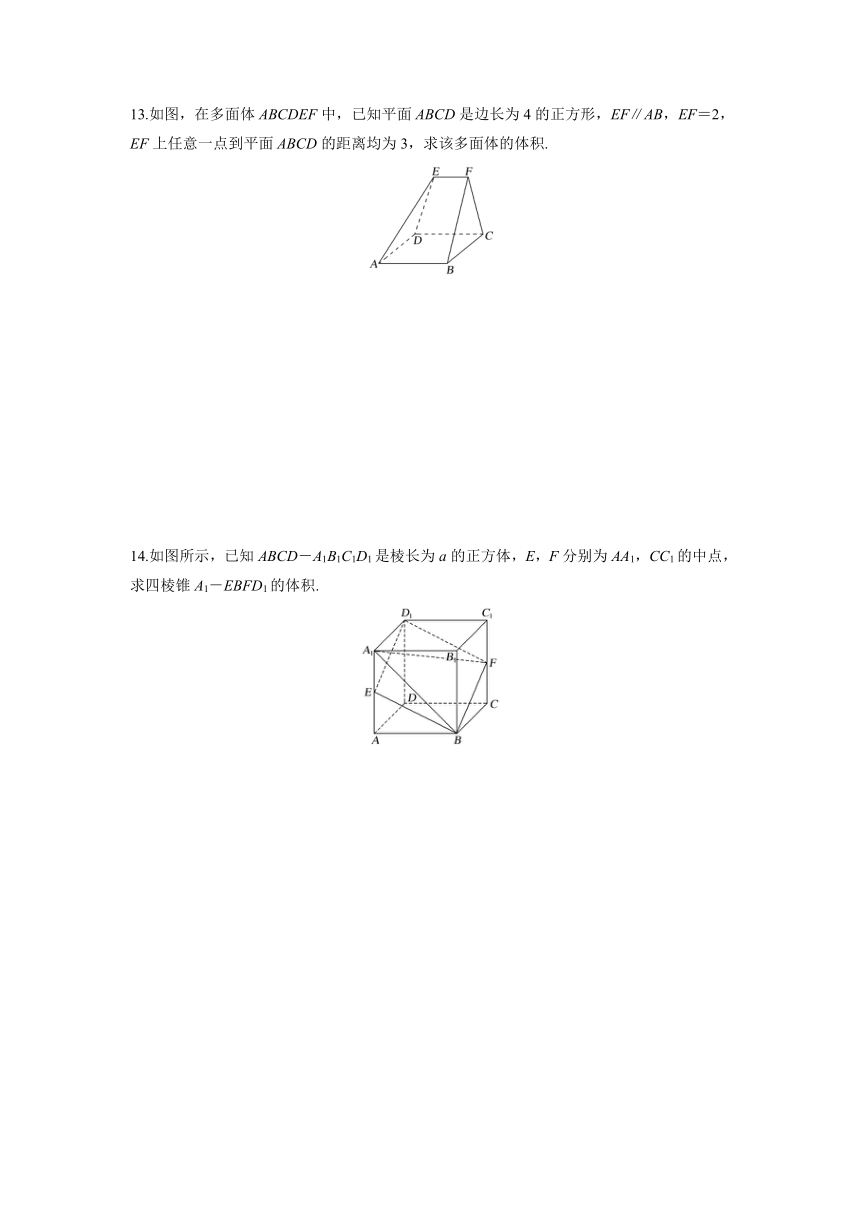
13.如图,在多面体ABCDEF中,已知平面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
14.如图所示,已知ABCD-A1B1C1D1是棱长为a的正方体,E,F分别为AA1,CC1的中点,求四棱锥A1-EBFD1的体积.
8.3.1 棱柱、棱锥、棱台的表面积和体积练习题-参考答案
1答案 C
解析 S=4××a·a=a2.
2答案 B
解析 V长方体=3×4×5=60(cm3).
3答案 B
解析 依题意,正三棱台的高
h==1.
4答案 B
解析 设棱柱的高为h,底面积为S,则棱锥的高为h,底面积为S,故二者的体积之比为===2.
5答案 D
解析 三棱锥B-A1B1C1与三棱锥A1-ABC的高相等,故其体积之比等于△A1B1C1与△ABC的面积之比,而△A1B1C1与△ABC的面积之比等于A1B1与AB之比的平方,即1∶4.
6答案 A
解析 依题设,正三棱锥的侧棱长为a,
∴S侧=3××=a2,S底=a2,
因此三棱锥的表面积S表=S侧+S底=a2.
7答案
解析 S△DD1E=DD1×1=,
又点F到平面DD1E的距离为1,
所以VD1-EDF=VF-D1DE=S△DD1E×1=.
8答案 1 012
解析 易知正四棱台侧面为等腰梯形,其高为=12,所以正四棱台的表面积S=4××(8+18)×12+82+182=1 012(cm2).
9答案
解析 如图,设点C到平面PAB的距离为h,则点E到平面BAD的距离为h.
∵S△DAB=S△PAB,
∴===.
10答案
解析 如图连接AC,BD,设AC和BD交于O,则O为点P在平面ABCD内的投影,即PO为四棱锥的高,
在△POC中,PC=4,OC=2,
则PO==2,
故V=Sh=×16×2=.
11答案 12,2 688
解析 O,O1分别是上底面和下底面的中心,E,E1分别是棱的中点,FE1⊥O1E1.
设OE=x cm,则上底面边长为2x cm,
下底面边长为(2x-10)cm,故O1E1=(x-5)cm,
则FE=5 cm.
又∵正四棱台的高是12 cm,
∴EE1=13 cm.
故正四棱台的全面积S=(2x)2+(2x-10)2+4×(2x+2x-10)×13=8(x2+8x-20)=512(cm2),
解得x=6 cm,
所以正四棱台上底面边长为12 cm,下底面边长为2 cm.
V台=×12×(122++22)=4×(144+24+4)=688(cm3).
12解 在三棱锥A1-ABD中,AA1⊥平面ABD,AB=AD=AA1=a,
A1B=BD=A1D=a,
∵V三棱锥A1-ABD=V三棱锥A-A1BD,
∴×a2·a=××a×·a·d.
∴d=a.
∴点A到平面A1BD的距离为a.
13解 如图,连接EB,EC,AC.
V四棱锥E-ABCD=×42×3=16.
∵AB=2EF,EF∥AB,
∴S△EAB=2S△BEF.
∴V三棱锥F-EBC=V三棱锥C-EFB
=V三棱锥C-ABE=V三棱锥E-ABC=×V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
14解 因为EB=BF=FD1=D1E= =a,
D1F∥EB,
所以四边形EBFD1是菱形.
连接EF,则△EFB≌△EFD1.
易知三棱锥A1-EFB与三棱锥A1-EFD1的高相等,
故VA1-EBFD1=2VA1-EFB=2VF-EBA1.
又因为S△EBA1=EA1·AB=a2,
则VF-EBA1=a3,
所以VA1-EBFD1=2VA1-EFB=2VF-EBA1=a3.
一、选择题
1.正三棱锥的所有棱长均为a,则该三棱锥的表面积为( )
A.3a2 B.2a2
C.a2 D.4a2
2.若长方体的长、宽、高分别为3 cm、4 cm、5 cm,则长方体的体积为( )
A.27 cm3 B.60 cm3
C.64 cm3 D.125 cm3
3.一个正三棱台的上、下底面边长分别为3和6,侧棱长为2,则其高为( )
A. B.1
C. D.
4.一个棱柱和一个棱锥的高相等,底面积之比为2∶3,则棱柱与棱锥的体积之比为( )
A. B.2
C. D.3
5.如图所示,三棱台ABC-A1B1C1中,A1B1∶AB=1∶2,则三棱锥B-A1B1C1与三棱锥A1-ABC的体积比为( )
A.1∶2 B.1∶3
C.1∶ D.1∶4
6.侧面都是等腰直角三角形的正三棱锥,底面边长为a时,该三棱锥的表面积是( )
A.a2 B.a2
C.a2 D.a2
二、填空题
7.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为________.
8.一个正四棱台,其上、下底面均为正方形,边长分别为8 cm和18 cm,侧棱长为13 cm,则其表面积为________ cm2.
9.三棱锥P-ABC中,D,E分别为PB,PC的中点,记三棱锥D-ABE的体积为V1,P-ABC的体积为V2,则=________.
10.如图所示,已知正四棱锥的侧棱长为4,底面边长为4,则该四棱锥的体积为________.
11.已知正四棱台的高是12 cm,两底面边长之差为10 cm,全面积为512 cm2,则上、下底面边长分别为________cm,体积为________cm3.
三、解答题
12.如图,在棱长为a的正方体ABCD-A1B1C1D1中,求点A到平面A1BD的距离d.
13.如图,在多面体ABCDEF中,已知平面ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.
14.如图所示,已知ABCD-A1B1C1D1是棱长为a的正方体,E,F分别为AA1,CC1的中点,求四棱锥A1-EBFD1的体积.
8.3.1 棱柱、棱锥、棱台的表面积和体积练习题-参考答案
1答案 C
解析 S=4××a·a=a2.
2答案 B
解析 V长方体=3×4×5=60(cm3).
3答案 B
解析 依题意,正三棱台的高
h==1.
4答案 B
解析 设棱柱的高为h,底面积为S,则棱锥的高为h,底面积为S,故二者的体积之比为===2.
5答案 D
解析 三棱锥B-A1B1C1与三棱锥A1-ABC的高相等,故其体积之比等于△A1B1C1与△ABC的面积之比,而△A1B1C1与△ABC的面积之比等于A1B1与AB之比的平方,即1∶4.
6答案 A
解析 依题设,正三棱锥的侧棱长为a,
∴S侧=3××=a2,S底=a2,
因此三棱锥的表面积S表=S侧+S底=a2.
7答案
解析 S△DD1E=DD1×1=,
又点F到平面DD1E的距离为1,
所以VD1-EDF=VF-D1DE=S△DD1E×1=.
8答案 1 012
解析 易知正四棱台侧面为等腰梯形,其高为=12,所以正四棱台的表面积S=4××(8+18)×12+82+182=1 012(cm2).
9答案
解析 如图,设点C到平面PAB的距离为h,则点E到平面BAD的距离为h.
∵S△DAB=S△PAB,
∴===.
10答案
解析 如图连接AC,BD,设AC和BD交于O,则O为点P在平面ABCD内的投影,即PO为四棱锥的高,
在△POC中,PC=4,OC=2,
则PO==2,
故V=Sh=×16×2=.
11答案 12,2 688
解析 O,O1分别是上底面和下底面的中心,E,E1分别是棱的中点,FE1⊥O1E1.
设OE=x cm,则上底面边长为2x cm,
下底面边长为(2x-10)cm,故O1E1=(x-5)cm,
则FE=5 cm.
又∵正四棱台的高是12 cm,
∴EE1=13 cm.
故正四棱台的全面积S=(2x)2+(2x-10)2+4×(2x+2x-10)×13=8(x2+8x-20)=512(cm2),
解得x=6 cm,
所以正四棱台上底面边长为12 cm,下底面边长为2 cm.
V台=×12×(122++22)=4×(144+24+4)=688(cm3).
12解 在三棱锥A1-ABD中,AA1⊥平面ABD,AB=AD=AA1=a,
A1B=BD=A1D=a,
∵V三棱锥A1-ABD=V三棱锥A-A1BD,
∴×a2·a=××a×·a·d.
∴d=a.
∴点A到平面A1BD的距离为a.
13解 如图,连接EB,EC,AC.
V四棱锥E-ABCD=×42×3=16.
∵AB=2EF,EF∥AB,
∴S△EAB=2S△BEF.
∴V三棱锥F-EBC=V三棱锥C-EFB
=V三棱锥C-ABE=V三棱锥E-ABC=×V四棱锥E-ABCD=4.
∴多面体的体积V=V四棱锥E-ABCD+V三棱锥F-EBC=16+4=20.
14解 因为EB=BF=FD1=D1E= =a,
D1F∥EB,
所以四边形EBFD1是菱形.
连接EF,则△EFB≌△EFD1.
易知三棱锥A1-EFB与三棱锥A1-EFD1的高相等,
故VA1-EBFD1=2VA1-EFB=2VF-EBA1.
又因为S△EBA1=EA1·AB=a2,
则VF-EBA1=a3,
所以VA1-EBFD1=2VA1-EFB=2VF-EBA1=a3.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
