人教版数学七年级下册 6.1.2 用计算器计算一个正数的算术平方根 课件(共20张PPT)
文档属性
| 名称 | 人教版数学七年级下册 6.1.2 用计算器计算一个正数的算术平方根 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
6.1.2 用计算器计算一个正数的算术平方根
第六章 实数
1.会用计算器求一个正数的算术平方根,知道算术平方根的小数点移动规律.
2.会估计一个含有根号的数的大小.
重点难点:
1.会用计算器求算术平方根.
2.掌握算术平方根的估算及大小比较.
学习目标:
情景导入
求一个正数的算术平方根,有些数可以直接得出结果,但有些数必须借助计算器,比如 0.46254. 那么如何借助计算器来求一个正数的算术平方根呢?这就是本堂课需要解决的问题.
知识精讲
知识点一 算术平方根的估算及大小比较
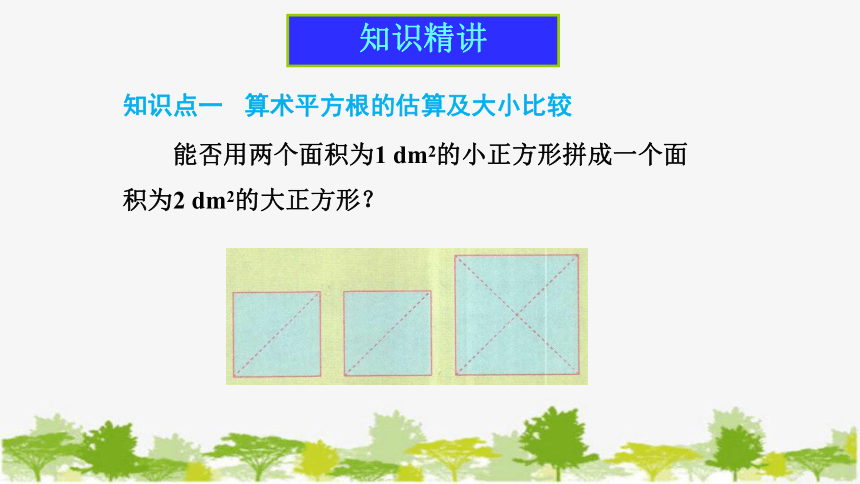
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形. 你知道这个大正方形的边长是多少吗?
设大正方形的边长为x dm,则x2 = 2.
由算术平方根的意义可知x= ,
所以大正方形的边长是 dm.
问题: 有多大?
因为 12 = 1,22=4,所以1< <2;
因为 1. 42 = 1. 96,1. 52=2. 25,所以 1.4< <1.5;
因为 1.412 = 1.988 1,1.422 = 2.016 4,
所以 1.41< <1.42;
因为 1. 4142 = 1. 999 396,1. 4152=2. 002 225,
所以 1.414< <1.415;
……
如此进行下去,可以得到 的更精确的近似值. 事实上, =1. 414 213 562 373…,它是一 个无限不循环小数.
实际上,许多正有理数的算术平方根(例如 等)都是无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
求一个正数(非完全平方数)的算术平方根的近似值,一般采用夹逼法.
“夹”就是从两边确定取值范围;“逼”就是一点一点加强限制,使其所处范围越来越小,从而达到理想的精确程度.
例1 小丽想用一块面积为 400 cm2的
正方形纸片,沿着边的方向裁出一块面
积为 300 cm2的长方形纸片,使它的长
宽之比为 3: 2. 她不知能否裁得出来,
正在发愁. 小明见了说:“别发愁,一定能用一块 面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系得3x 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大于21 cm.
因为 =20,所以正方形纸片的边长只有20 cm. 这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法. 小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
针对练习
1.估算 -2的值 ( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
B
2.通过估算比较下列各组数的大小:
(1) 与1.9; (2) 与1.5.
解:(1)因为5>4,所以 >2,所以 >1.9.
(2)因为6>4,所以 > 2,所以 > =1.5.
知识点二 用计算器求一个正数的算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
… …
… …
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
用计算器求下列各式的值:
(1) ; (2) (精确到 0.001).
例2
解:(1)依次按键 3136 ,
显示:56.
∴ =56.
(2)依次按键, 2 ,
显示:1.414 213 562.
∴ ≈1.414.
针对练习
1.用计算器求下列各式的值:
(1) ; (2) ; (3) (精确到 0.01).
解:
当堂检测
1.在计算器上按键 ,下列计算结果正确的是 ( )
A. 3 B. -3 C. -1 D. 1
2. 估计 在 ( )
A. 2~3之间 B. 3~4之间
C. 4~5之间 D. 5~6之间
B
C
3. 设n为正整数,且n<A. 5 B. 6 C. 7 D. 8
4.与 最接近的整数是 ( )
A. 4 B. 5 C. 6 D. 7
D
C
5.计算 的结果精确到0.01是(可用科学计算器计算或笔算)( )
A.0.30 B.0.31
C.0.32 D.0.33
C
6.比较下列各组数的大小:
(1) 与 ; (2) 与 8;
(3) 与 0.5; (4) 与 1.
解:(1) < (2) > 8
(3) > 0.5 (4) < 1
7.已知 2+ 的小数部分为 a,5 – 的小数部分为 b,求 a+b 的值.
解:∵1 < < 2,∴3 <2+ < 4,
∴a = 2 + – 3 = – 1,
∵1 < < 2,∴3 < 5 – < 4,
∴b = 5 – – 3 = 2 – ,
∴a + b = – 1 + 2 – = 1.
课堂小结
用计算器开方
使用计算器进行开方运算
用计算器开方比较数的大小
ON
=
2
∵1 < 2 < 4
∴1 < < 2
6.1.2 用计算器计算一个正数的算术平方根
第六章 实数
1.会用计算器求一个正数的算术平方根,知道算术平方根的小数点移动规律.
2.会估计一个含有根号的数的大小.
重点难点:
1.会用计算器求算术平方根.
2.掌握算术平方根的估算及大小比较.
学习目标:
情景导入
求一个正数的算术平方根,有些数可以直接得出结果,但有些数必须借助计算器,比如 0.46254. 那么如何借助计算器来求一个正数的算术平方根呢?这就是本堂课需要解决的问题.
知识精讲
知识点一 算术平方根的估算及大小比较
能否用两个面积为1 dm2的小正方形拼成一个面积为2 dm2的大正方形?
如图,把两个小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,就得到一个面积为2 dm2的大正方形. 你知道这个大正方形的边长是多少吗?
设大正方形的边长为x dm,则x2 = 2.
由算术平方根的意义可知x= ,
所以大正方形的边长是 dm.
问题: 有多大?
因为 12 = 1,22=4,所以1< <2;
因为 1. 42 = 1. 96,1. 52=2. 25,所以 1.4< <1.5;
因为 1.412 = 1.988 1,1.422 = 2.016 4,
所以 1.41< <1.42;
因为 1. 4142 = 1. 999 396,1. 4152=2. 002 225,
所以 1.414< <1.415;
……
如此进行下去,可以得到 的更精确的近似值. 事实上, =1. 414 213 562 373…,它是一 个无限不循环小数.
实际上,许多正有理数的算术平方根(例如 等)都是无限不循环小数.
无限不循环小数是指小数位数无限,且小数部分不循环的小数.
求一个正数(非完全平方数)的算术平方根的近似值,一般采用夹逼法.
“夹”就是从两边确定取值范围;“逼”就是一点一点加强限制,使其所处范围越来越小,从而达到理想的精确程度.
例1 小丽想用一块面积为 400 cm2的
正方形纸片,沿着边的方向裁出一块面
积为 300 cm2的长方形纸片,使它的长
宽之比为 3: 2. 她不知能否裁得出来,
正在发愁. 小明见了说:“别发愁,一定能用一块 面积大的纸片裁出一块面积小的纸片.”你同意小明的说法吗?小丽能用这块纸片裁出符合要求的纸片吗?
解:设长方形纸片的长为3x cm,宽为2x cm. 根据边长与面积的关系得3x 2x=300,6x2 =300, x2 =50, x = .
因此长方形纸片的长为 cm.
因为50>49,所以 >7.
由上可知 >21,即长方形纸片的长应该大于21 cm.
因为 =20,所以正方形纸片的边长只有20 cm. 这样,长方形纸片的长将大于正方形纸片的边长.
答:不能同意小明的说法. 小丽不能用这块正方形纸片裁出符合要求的长方形纸片.
针对练习
1.估算 -2的值 ( )
A.在1和2之间 B.在2和3之间
C.在3和4之间 D.在4和5之间
B
2.通过估算比较下列各组数的大小:
(1) 与1.9; (2) 与1.5.
解:(1)因为5>4,所以 >2,所以 >1.9.
(2)因为6>4,所以 > 2,所以 > =1.5.
知识点二 用计算器求一个正数的算术平方根
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数a的算术平方根(或其近似数).
a
=
按键顺序:
… …
… …
规律:被开方数的小数点向右每移动 位,它的算术平方根的小数点就向右移动 位;被开方数的小数点向左每移动 位,它的算术平方根的小数点就向左移动 位.
利用计算器计算下表中的算术平方根,并将计算结果填在表中,你发现了什么规律 你能说出其中的道理吗
用计算器求下列各式的值:
(1) ; (2) (精确到 0.001).
例2
解:(1)依次按键 3136 ,
显示:56.
∴ =56.
(2)依次按键, 2 ,
显示:1.414 213 562.
∴ ≈1.414.
针对练习
1.用计算器求下列各式的值:
(1) ; (2) ; (3) (精确到 0.01).
解:
当堂检测
1.在计算器上按键 ,下列计算结果正确的是 ( )
A. 3 B. -3 C. -1 D. 1
2. 估计 在 ( )
A. 2~3之间 B. 3~4之间
C. 4~5之间 D. 5~6之间
B
C
3. 设n为正整数,且n<
4.与 最接近的整数是 ( )
A. 4 B. 5 C. 6 D. 7
D
C
5.计算 的结果精确到0.01是(可用科学计算器计算或笔算)( )
A.0.30 B.0.31
C.0.32 D.0.33
C
6.比较下列各组数的大小:
(1) 与 ; (2) 与 8;
(3) 与 0.5; (4) 与 1.
解:(1) < (2) > 8
(3) > 0.5 (4) < 1
7.已知 2+ 的小数部分为 a,5 – 的小数部分为 b,求 a+b 的值.
解:∵1 < < 2,∴3 <2+ < 4,
∴a = 2 + – 3 = – 1,
∵1 < < 2,∴3 < 5 – < 4,
∴b = 5 – – 3 = 2 – ,
∴a + b = – 1 + 2 – = 1.
课堂小结
用计算器开方
使用计算器进行开方运算
用计算器开方比较数的大小
ON
=
2
∵1 < 2 < 4
∴1 < < 2
