北师大版九年级数学《圆》单元测试一(有答案)
文档属性
| 名称 | 北师大版九年级数学《圆》单元测试一(有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 194.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-16 00:00:00 | ||
图片预览

文档简介
北师大版九年级数学《圆》单元测试一
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
2.两圆半径R、r分别是方程的两根,且圆心距,则两圆的位置关系是( )
A.外离 B.外切 C.内含 D.外离或内含
3.P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若,都是整数,则这样的点共有( )
A.4个 B.8个 C.12个 D.16个
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
5.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
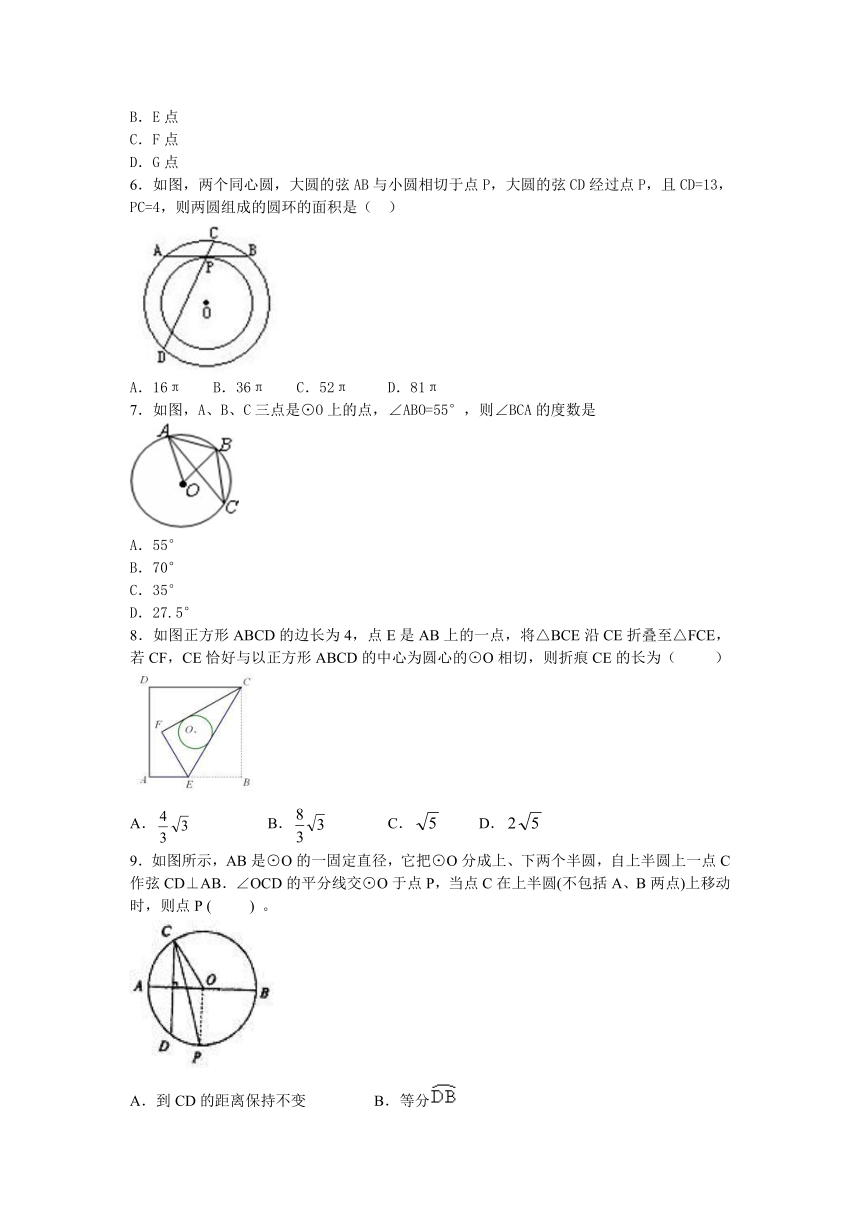
6.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
7.如图,A、B、C三点是⊙O上的点,∠ABO=55°,则∠BCA的度数是
A.55°
B.70°
C.35°
D.27.5°
8.如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
A. B. C. D.
9.如图所示,AB是⊙O的一固定直径,它把⊙O分成上、下两个半圆,自上半圆上一点C作弦CD⊥AB.∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,则点P ( ) 。
A.到CD的距离保持不变 B.等分
C.随C点的移动而移动 D.位置不变
10.在直角坐标系x0y中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )个
A、1个 B、2个 C、3个 D、4个
二、填空题
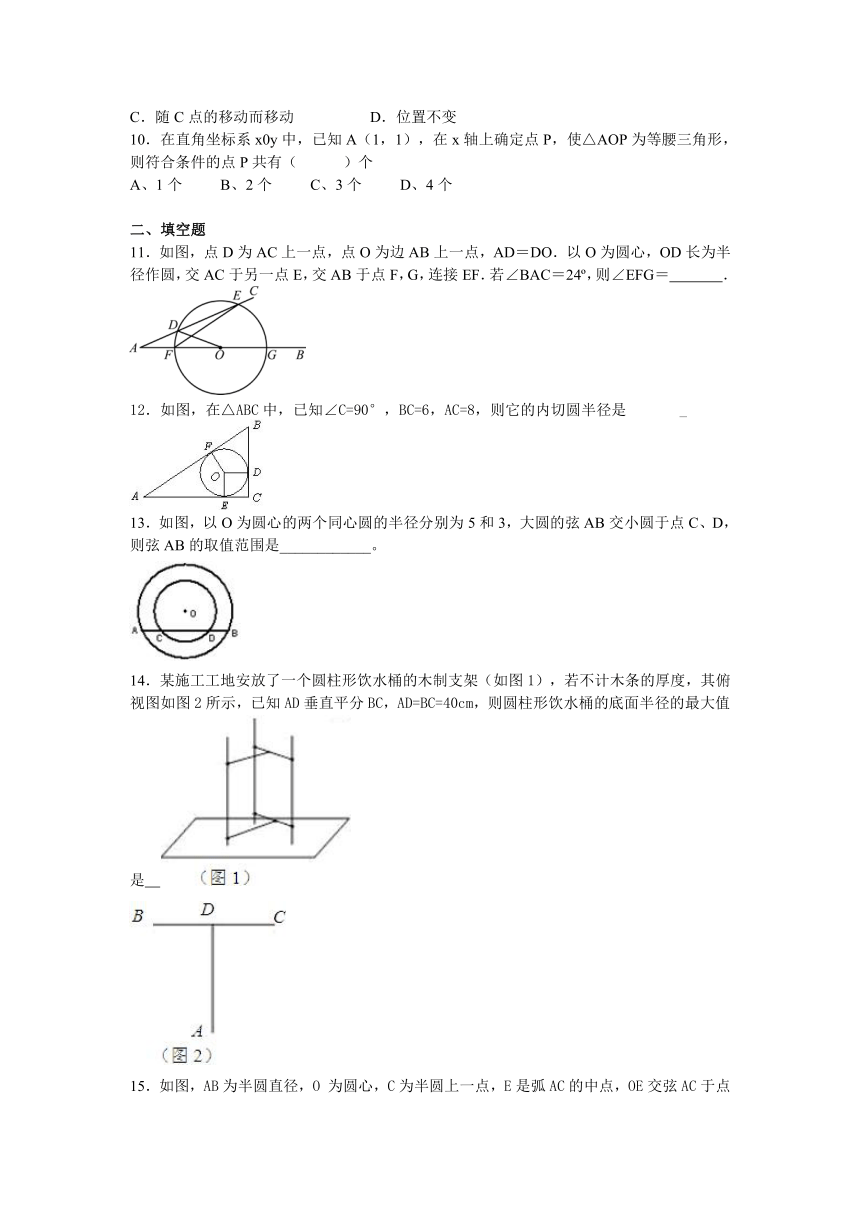
11.如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24o,则∠EFG= .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是____________。
14.某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=40cm,则圆柱形饮水桶的底面半径的最大值是
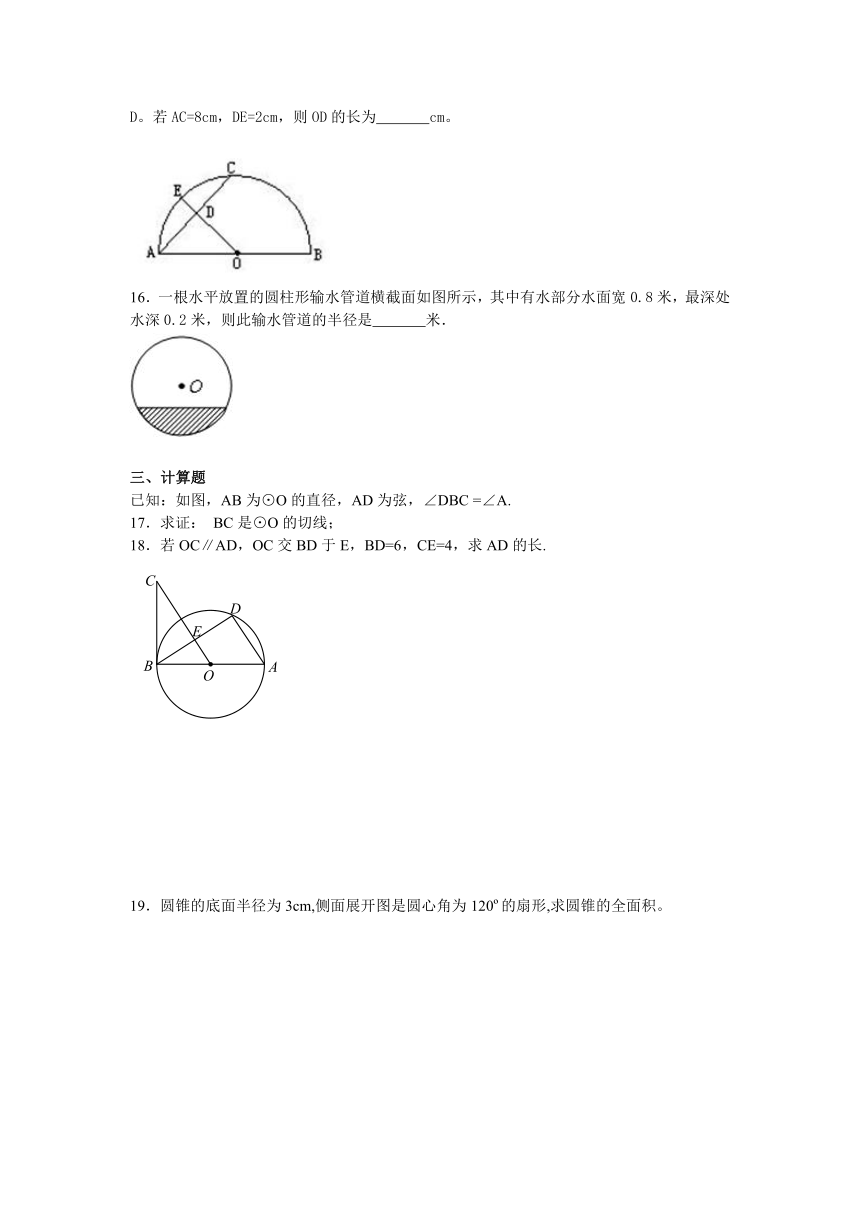
15.如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D。若AC=8cm,DE=2cm,则OD的长为 cm。
16.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的半径是 米.
三、计算题
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
17.求证: BC是⊙O的切线;
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
19.圆锥的底面半径为3cm,侧面展开图是圆心角为120o的扇形,求圆锥的全面积。
四、解答题
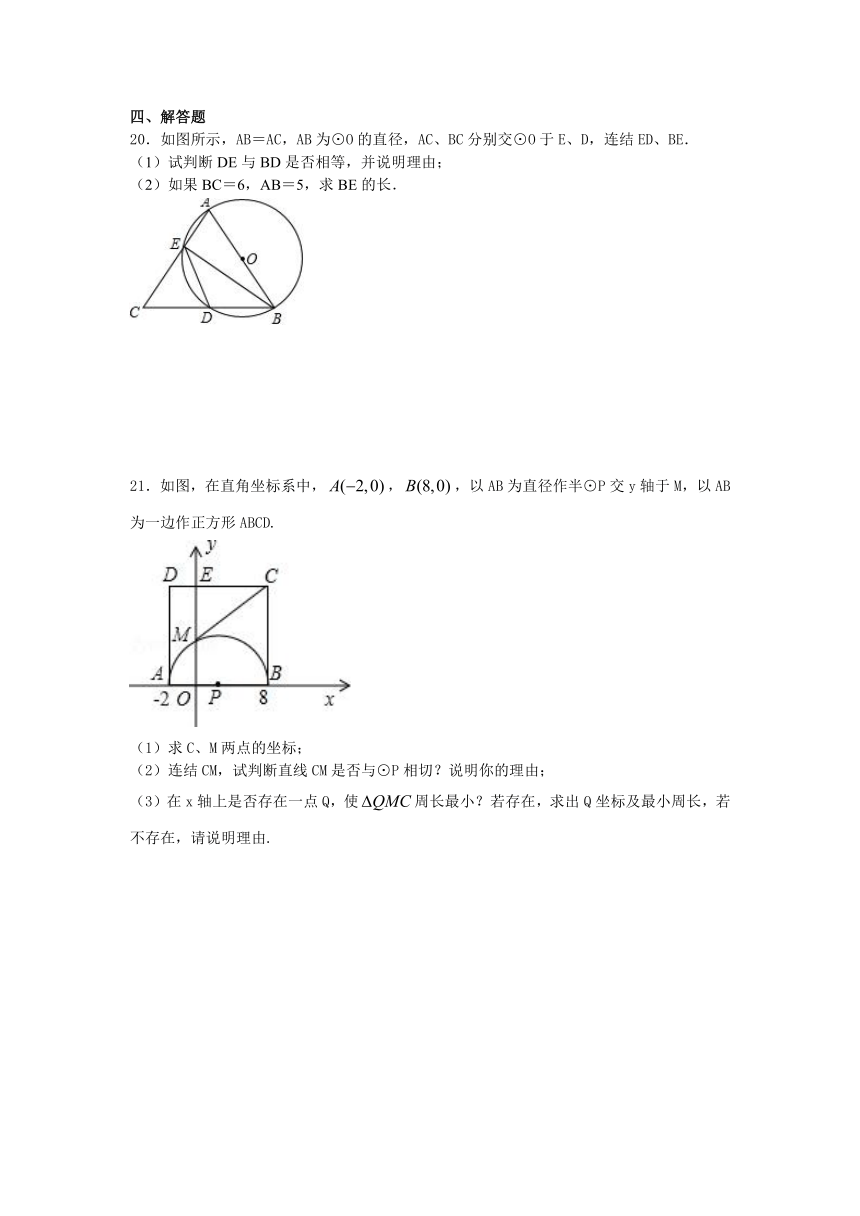
20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
21.如图,在直角坐标系中,,,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.
(1)求C、M两点的坐标;
(2)连结CM,试判断直线CM是否与⊙P相切?说明你的理由;
(3)在x轴上是否存在一点Q,使周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.
22.如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?
23.如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.(本题10分)
24.如图,AB是⊙O的弦(非直径),C、D是AB上的两点,并且AC=BD。求证:OC=OD。
25.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)判断线段AC与AE是否相等,并说明理由;
(2)求过A、C、D三点的圆的直径.
26.在△BDF中,BD=BF,以为直径的与边DF相交于点,过E作BF的垂线,垂足为C,交BD延长线于点A.
(1)求证:AC与⊙O相切.
(2)若,求的半径.
参考答案
1.D
2.B
3.C
4.A
5.A
6.B
7.C
8.B
9.D
10.D
11.36o
12.2
13.
14.25
15.3
16.0.5
17.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.
20.(1)DE=BD;(2)4.8
21.(1)C(8,10),M(0,4);(2)相切;(3),
22.(1)9;1;(2)3秒、秒、11秒、13秒
23.略
24.略
25.(1)AC=AE;(2)
26.(1)略
(2),(舍去) …… 8分 答:略
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,已知AB是⊙O的直径,CD是弦,AB⊥CD于点E,若AB=10,CD = 6,则BE的长是( )
A.4 B.3 C.2 D.1
2.两圆半径R、r分别是方程的两根,且圆心距,则两圆的位置关系是( )
A.外离 B.外切 C.内含 D.外离或内含
3.P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若,都是整数,则这样的点共有( )
A.4个 B.8个 C.12个 D.16个
4.形如半圆型的量角器直径为4cm,放在如图所示的平面直角坐标系中(量角器的中心与坐标原点O重合,零刻度线在x轴上),连接60°和120°刻度线的外端点P、Q,线段PQ交y轴于点A,则点A的坐标为 ( )
A.(0,) B.(-1,) C.(,0) D.(1,)
5.如图,两个半径都是4cm的圆外切于点C,一只蚂蚁由点A开始依A、B、C、D、E、F、C、G、A的顺序沿着圆周上的8段长度相等的路径绕行,蚂蚁在这8段路径上不断爬行,直到行走2006πcm后才停下来,则蚂蚁停的那一个点为( )
A.D点
B.E点
C.F点
D.G点
6.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
7.如图,A、B、C三点是⊙O上的点,∠ABO=55°,则∠BCA的度数是
A.55°
B.70°
C.35°
D.27.5°
8.如图正方形ABCD的边长为4,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )
A. B. C. D.
9.如图所示,AB是⊙O的一固定直径,它把⊙O分成上、下两个半圆,自上半圆上一点C作弦CD⊥AB.∠OCD的平分线交⊙O于点P,当点C在上半圆(不包括A、B两点)上移动时,则点P ( ) 。
A.到CD的距离保持不变 B.等分
C.随C点的移动而移动 D.位置不变
10.在直角坐标系x0y中,已知A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P共有( )个
A、1个 B、2个 C、3个 D、4个
二、填空题
11.如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半径作圆,交AC于另一点E,交AB于点F,G,连接EF.若∠BAC=24o,则∠EFG= .
12.如图,在△ABC中,已知∠C=90°,BC=6,AC=8,则它的内切圆半径是 _
13.如图,以O为圆心的两个同心圆的半径分别为5和3,大圆的弦AB交小圆于点C、D,则弦AB的取值范围是____________。
14.某施工工地安放了一个圆柱形饮水桶的木制支架(如图1),若不计木条的厚度,其俯视图如图2所示,已知AD垂直平分BC,AD=BC=40cm,则圆柱形饮水桶的底面半径的最大值是
15.如图,AB为半圆直径,O 为圆心,C为半圆上一点,E是弧AC的中点,OE交弦AC于点D。若AC=8cm,DE=2cm,则OD的长为 cm。
16.一根水平放置的圆柱形输水管道横截面如图所示,其中有水部分水面宽0.8米,最深处水深0.2米,则此输水管道的半径是 米.
三、计算题
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
17.求证: BC是⊙O的切线;
18.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
19.圆锥的底面半径为3cm,侧面展开图是圆心角为120o的扇形,求圆锥的全面积。
四、解答题
20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连结ED、BE.
(1)试判断DE与BD是否相等,并说明理由;
(2)如果BC=6,AB=5,求BE的长.
21.如图,在直角坐标系中,,,以AB为直径作半⊙P交y轴于M,以AB为一边作正方形ABCD.
(1)求C、M两点的坐标;
(2)连结CM,试判断直线CM是否与⊙P相切?说明你的理由;
(3)在x轴上是否存在一点Q,使周长最小?若存在,求出Q坐标及最小周长,若不存在,请说明理由.
22.如图,点A、B在直线MN上,AB=11cm,⊙A、⊙B的半径为1cm. ⊙A以每秒2cm的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(cm)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)当t=1时,AB= cm;当t=6时,AB= cm;
(2)问点A出发后多少秒两圆相切?
23.如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D.
(1)求证:AD平分∠BAC;
(2)若BE=2,BD=4,求⊙O的半径.(本题10分)
24.如图,AB是⊙O的弦(非直径),C、D是AB上的两点,并且AC=BD。求证:OC=OD。
25.如图,在Rt△ABC中,∠ACB=90°,AC=5,CB=12,AD是△ABC的角平分线,过A、C、D三点的圆与斜边AB交于点E,连接DE.
(1)判断线段AC与AE是否相等,并说明理由;
(2)求过A、C、D三点的圆的直径.
26.在△BDF中,BD=BF,以为直径的与边DF相交于点,过E作BF的垂线,垂足为C,交BD延长线于点A.
(1)求证:AC与⊙O相切.
(2)若,求的半径.
参考答案
1.D
2.B
3.C
4.A
5.A
6.B
7.C
8.B
9.D
10.D
11.36o
12.2
13.
14.25
15.3
16.0.5
17.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
18.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
19.
20.(1)DE=BD;(2)4.8
21.(1)C(8,10),M(0,4);(2)相切;(3),
22.(1)9;1;(2)3秒、秒、11秒、13秒
23.略
24.略
25.(1)AC=AE;(2)
26.(1)略
(2),(舍去) …… 8分 答:略
