北师大版九年级数学《圆》单元测试三(有答案)
文档属性
| 名称 | 北师大版九年级数学《圆》单元测试三(有答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 284.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-16 00:00:00 | ||
图片预览


文档简介
北师大版九年级数学《圆》单元测试三
学校:___________姓名:___________班级:___________考号:___________
一、选择题
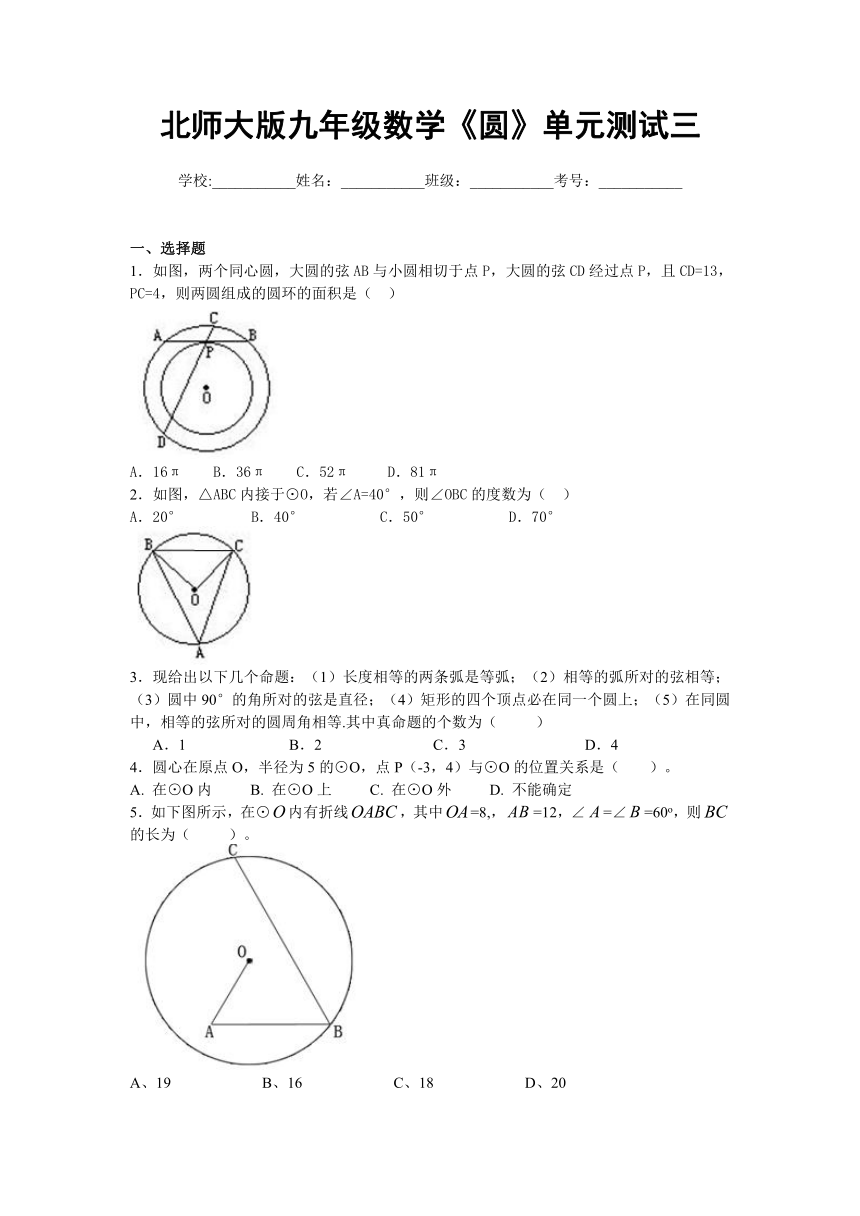
1.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
2.如图,△ABC内接于⊙O,若∠A=40°,则∠OBC的度数为( )
A.20° B.40° C.50° D.70°
3.现给出以下几个命题:(1)长度相等的两条弧是等弧;(2)相等的弧所对的弦相等;(3)圆中90°的角所对的弦是直径;(4)矩形的四个顶点必在同一个圆上;(5)在同圆中,相等的弦所对的圆周角相等.其中真命题的个数为( )
A.1 B.2 C.3 D.4
4.圆心在原点O,半径为5的⊙O,点P(-3,4)与⊙O的位置关系是( )。
A. 在⊙O内 B. 在⊙O上 C. 在⊙O外 D. 不能确定
5.如下图所示,在⊙内有折线,其中=8,,=12,∠=∠=60o,则的长为( )。
A、19 B、16 C、18 D、20
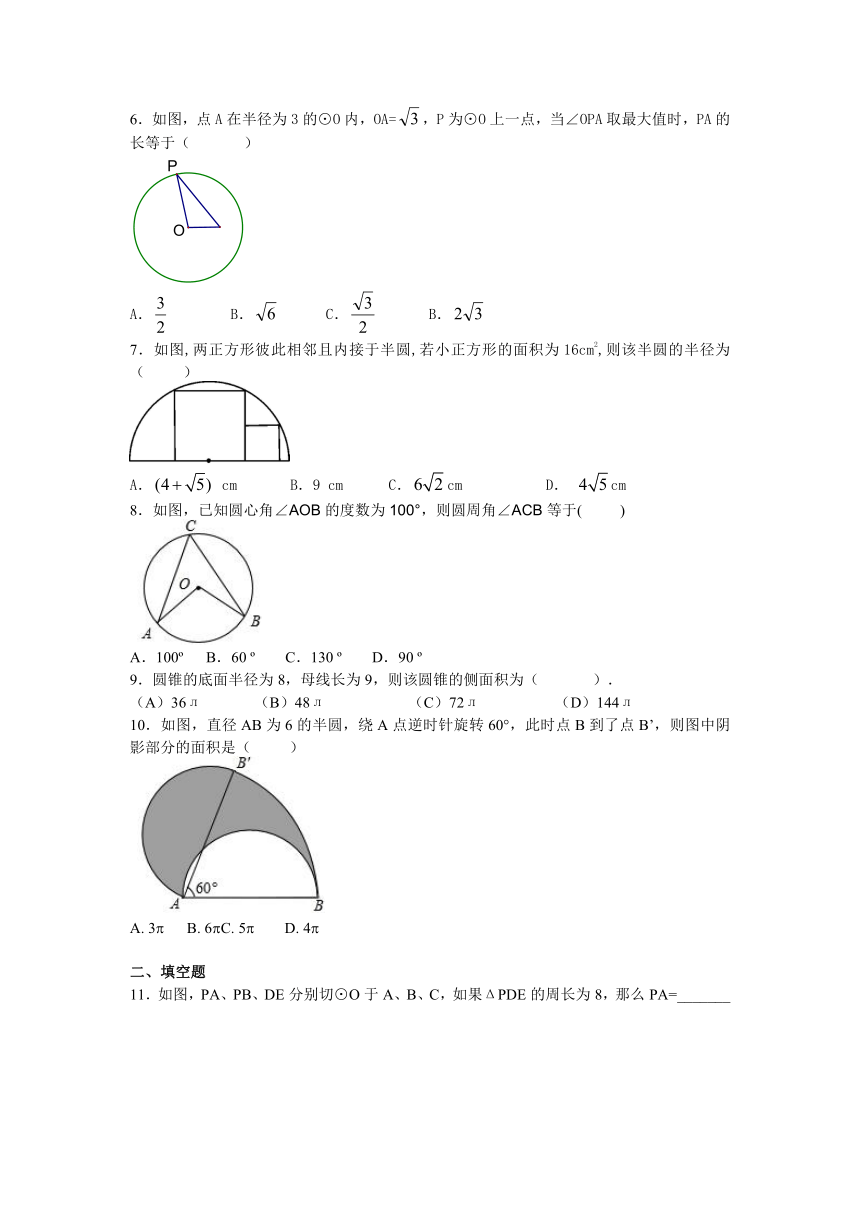
6.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,当∠OPA取最大值时,PA的长等于( )
A. B. C. B.
7.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A. cm B.9 cm C.cm D. cm
8.如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于( )
A.100o B.60 o C.130 o D.90 o
9.圆锥的底面半径为8,母线长为9,则该圆锥的侧面积为( ).
(A)36л (B)48л (C)72л (D)144л
10.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B’,则图中阴影部分的面积是( )
A. 3( B. 6( C. 5( D. 4(
二、填空题
11.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
12.如图,小红要制作一个高为8cm,底面圆直径是12cm的圆锥形小漏斗,若不计接缝,不计损耗,则她所需纸板的面积是 cm2.
13.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
14.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为 。
15.如图,半径为2的圆形纸片,沿半径OA、OB裁成1:3两部分,用得到的扇形围成圆锥的侧面,则圆锥的底面半径分别为 。
16.如下图,已知、两点的坐标分别是 (,0)(0,2),是△外接圆上的一点,且∠=45o,则点的坐标是 。
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
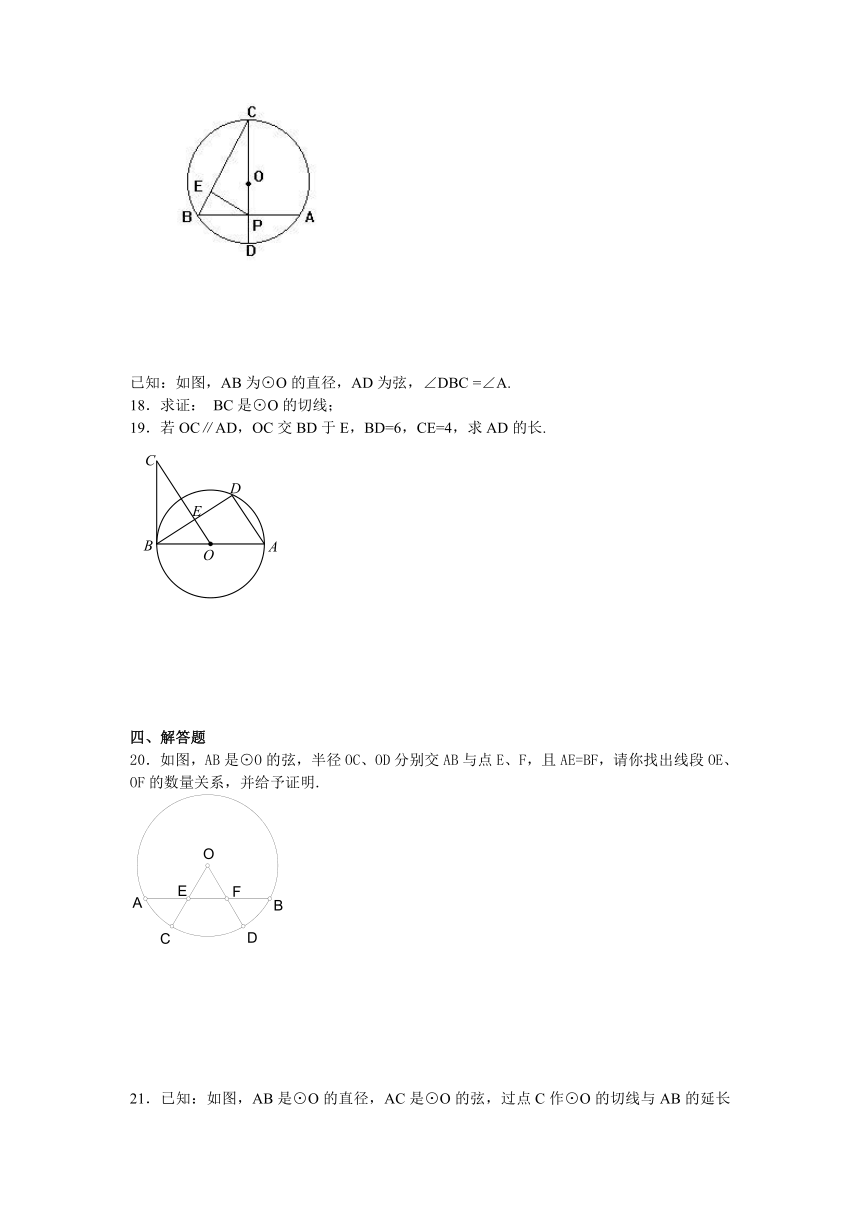
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
18.求证: BC是⊙O的切线;
19.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
20.如图,AB是⊙O的弦,半径OC、OD分别交AB与点E、F,且AE=BF,请你找出线段OE、OF的数量关系,并给予证明.
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线与AB的延长线交于点D。若∠CAB=30°,AB=30,求BD的长。
22.如图,AD、BC是⊙O的两条弦,且AD=BC,求证:AB=CD。
23.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1) 请在图中确定该圆弧所在圆心D点的位置,D点坐标为________;
(2) 连接AD、CD,求⊙D的半径(结果保留根号)及扇形ADC的圆心角度数;
(3) 若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径 (结果保留根号).
24.已知:如图,∠MAN=45°,B为AM上的一个定点, 若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C,请确定⊙P的位置,使BC恰与⊙P相切.
(1)画出图形(不要求尺规作图,不要求写画法);
(2)连结BP并填空:
① ∠ABC= °;
② 比较大小:∠ABP ∠CBP.(用“>”、“<”或“=”连接)
25.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
26.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
参考答案
1.B
2.C
3.B
4.B
5.D
6.B
7.D
8.C
9.C
10.B
11.4
12.60π
13.
14.8
15.
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
19.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
20.OE=OF
21.BD=15
22.见解析
23.(1) D(2,0);(2)半径为,圆心角为90度;(3)
24. <
25.证明见解析 AE=1.5
26.(1)EF∥AC;(2)四边形ADEG为矩形。
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PC=4,则两圆组成的圆环的面积是( )
A.16π B.36π C.52π D.81π
2.如图,△ABC内接于⊙O,若∠A=40°,则∠OBC的度数为( )
A.20° B.40° C.50° D.70°
3.现给出以下几个命题:(1)长度相等的两条弧是等弧;(2)相等的弧所对的弦相等;(3)圆中90°的角所对的弦是直径;(4)矩形的四个顶点必在同一个圆上;(5)在同圆中,相等的弦所对的圆周角相等.其中真命题的个数为( )
A.1 B.2 C.3 D.4
4.圆心在原点O,半径为5的⊙O,点P(-3,4)与⊙O的位置关系是( )。
A. 在⊙O内 B. 在⊙O上 C. 在⊙O外 D. 不能确定
5.如下图所示,在⊙内有折线,其中=8,,=12,∠=∠=60o,则的长为( )。
A、19 B、16 C、18 D、20
6.如图,点A在半径为3的⊙O内,OA=,P为⊙O上一点,当∠OPA取最大值时,PA的长等于( )
A. B. C. B.
7.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为( )
A. cm B.9 cm C.cm D. cm
8.如图,已知圆心角∠AOB的度数为100°,则圆周角∠ACB等于( )
A.100o B.60 o C.130 o D.90 o
9.圆锥的底面半径为8,母线长为9,则该圆锥的侧面积为( ).
(A)36л (B)48л (C)72л (D)144л
10.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B’,则图中阴影部分的面积是( )
A. 3( B. 6( C. 5( D. 4(
二、填空题
11.如图,PA、PB、DE分别切⊙O于A、B、C,如果ΔPDE的周长为8,那么PA=_______
12.如图,小红要制作一个高为8cm,底面圆直径是12cm的圆锥形小漏斗,若不计接缝,不计损耗,则她所需纸板的面积是 cm2.
13.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为 cm.
14.已知等腰△ABC的三个顶点都在半径为5的⊙O上,如果底边BC的长为8,那么BC边上的高为 。
15.如图,半径为2的圆形纸片,沿半径OA、OB裁成1:3两部分,用得到的扇形围成圆锥的侧面,则圆锥的底面半径分别为 。
16.如下图,已知、两点的坐标分别是 (,0)(0,2),是△外接圆上的一点,且∠=45o,则点的坐标是 。
三、计算题
17.
又PE⊥CB于E,若BC=10,且CE∶EB=3∶2,求AB的长.
已知:如图,AB为⊙O的直径,AD为弦,∠DBC =∠A.
18.求证: BC是⊙O的切线;
19.若OC∥AD,OC交BD于E,BD=6,CE=4,求AD的长.
四、解答题
20.如图,AB是⊙O的弦,半径OC、OD分别交AB与点E、F,且AE=BF,请你找出线段OE、OF的数量关系,并给予证明.
21.已知:如图,AB是⊙O的直径,AC是⊙O的弦,过点C作⊙O的切线与AB的延长线交于点D。若∠CAB=30°,AB=30,求BD的长。
22.如图,AD、BC是⊙O的两条弦,且AD=BC,求证:AB=CD。
23.如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1) 请在图中确定该圆弧所在圆心D点的位置,D点坐标为________;
(2) 连接AD、CD,求⊙D的半径(结果保留根号)及扇形ADC的圆心角度数;
(3) 若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径 (结果保留根号).
24.已知:如图,∠MAN=45°,B为AM上的一个定点, 若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C,请确定⊙P的位置,使BC恰与⊙P相切.
(1)画出图形(不要求尺规作图,不要求写画法);
(2)连结BP并填空:
① ∠ABC= °;
② 比较大小:∠ABP ∠CBP.(用“>”、“<”或“=”连接)
25.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于点D、E,连结EB交OD于点F.
(1)求证:OD⊥BE;
(2)若DE=,AB=,求AE的长.
26.如图,在等边△ABC中,AD⊥BC于点D,一个直径与AD相等的圆与BC相切于点E,与AB相切于点F,连接EF。
(1)判断EF与AC的位置关系(不必说明理由);;
(2)如图(2),过E作BC的垂线,交圆于G,连接AG,判断四边形ADEG的形状,并说明理由。
(3)求证:AC与GE的交点O为此圆的圆心.
参考答案
1.B
2.C
3.B
4.B
5.D
6.B
7.D
8.C
9.C
10.B
11.4
12.60π
13.
14.8
15.
16.
17.
∴CD⊥AB
又∵BC=10
CE∶EB=3∶2
∴EC=6,BE=4
又∵PE⊥BC
∴Rt△BEP∽Rt△BPC
18.证明:(1)∵AB为⊙O的直径
∴(D=90°, (A+(ABD=90°
∵∠DBC =∠A
∴∠DBC+∠ABD=90°
∴BC⊥AB
∴BC是⊙O的切线
19.∵OC∥AD,(D=90°,BD=6
∴OC⊥BD
∴BE=BD=3
∵O是AB的中点
∴AD=2EO -
∵BC⊥AB ,OC⊥BD
∴△CEB∽△BEO,∴
∵CE=4, ∴
∴AD=
20.OE=OF
21.BD=15
22.见解析
23.(1) D(2,0);(2)半径为,圆心角为90度;(3)
24. <
25.证明见解析 AE=1.5
26.(1)EF∥AC;(2)四边形ADEG为矩形。
