华师大版八年级数学下册试题一课一练19.2.1菱形的性质(Word版,含答案)
文档属性
| 名称 | 华师大版八年级数学下册试题一课一练19.2.1菱形的性质(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 332.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览




文档简介
19.2.1《菱形的性质》
第一课时
一、选择题
1. 若菱形的一条对角线长是另一条对角线长的2倍,且此菱形的面积为,则它的边长是( )
A. B. C. D.
2. 如图,在菱形中,为的中点,作,交于点,如果,那么长为( )
A.10 B.4 C.6 D.8
3. 如图,在菱形中,,的垂直平分线交对角线于点,为垂足,连结,则等于( )
A. B. C. D.
4. 如图所示,在菱形中,,周长为,则较长的对角线长为( )
A. B. C. D.
5. 菱形中,若,的平分线与边间的关系是
( )
A.相等 B.互相平分但不垂直
C.互相垂直但不平分 D.垂直平分
6. 菱形周长为,两条对角线的差为,则该菱形面积为( )
A. B. C. D.
7. 若菱形周长52cm,一条对角线长24cm,则它的面积是( ).
A.60 B.80 C.120 D.40
8. 如图,菱形中,对角线相交于点,则下列性质:
①;
②,且;
③;
④,.
其中菱形一定具有的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9. 菱形中,对角线与交于点,则下列说法不正确的是( )
A. B.
C. D.
10. 菱形具有而矩形不一定有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线互相垂直
11. 菱形的周长等于它的高的8倍,则它各个角是( )
A.和 B.和
C.和 D.和
12. 若菱形的一条对角线是另一条对角线长的2倍,且此菱形的面积为16,则它的边长为( )
A.4 B.2 C. D.
13. 菱形和矩形一定都具有的性质是( )
A.对角线相等. B.对角线互相平分.
C.对角线互相垂直. D.每条对角线平分一组对角.
二、填空题
14. 菱形周长为24cm,高为3cm,则菱形相邻两角的度数分别为 .
15. 已知菱形两条对角线之比为,它们的差为,则菱形的面积是________.
16. 如图,在菱形ABCD中,对角线AC=6,BD=8,则菱形的高为_______.
17. 已知菱形的周长为,两条对角线长的比为,则此菱形两条对角线的长分别为 .
18. 已知菱形的边长为6,,如果点是菱形内一点,且,那么的长为 .
19. 已知菱形的一条对角线长为4cm,周长为16cm,则菱形的四个角分别为 .
20. 菱形的四条边_________对角线__________且每一条对角线__________.
21. 菱形的两条对角线把菱形分割成一些三角形,其中直角三角形有_________个.
22. 菱形的对线交于点,则图中等腰三角形的个数是________个.
23. 已知菱形的周长为,两个相邻角之比为,则较短对角线长为__________.
24. 菱形中,点到边所在直线的距离 .
25. 在菱形中,交于,,,则菱形的周长为 .
26. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是______.
27. 已知菱形的两条对角线的长都是8cm,则菱形的边长为 cm.
28. 在菱形ABCD中,AE、AF分别垂直平分边BC、CD,则∠EAF= .
三、证明题
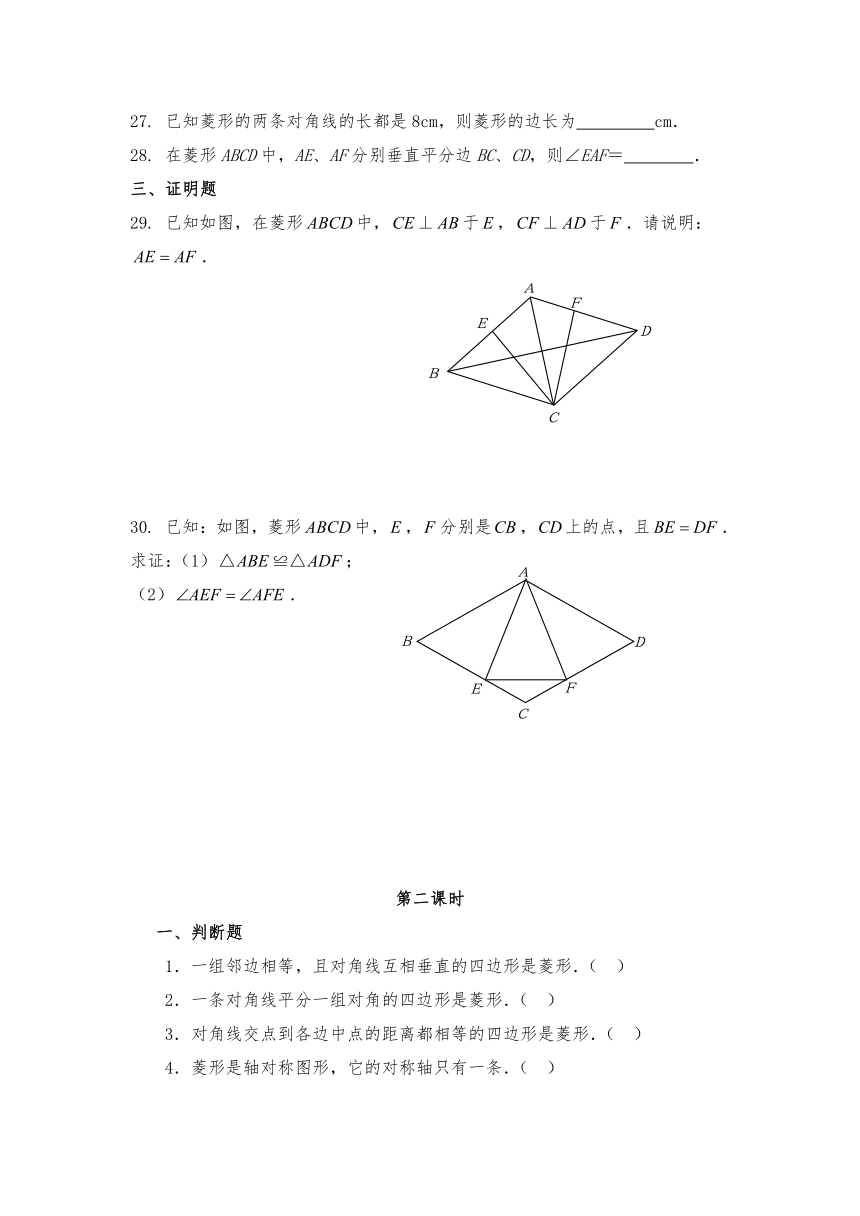
29. 已知如图,在菱形中,于,于.请说明:.
30. 已知:如图,菱形中,,分别是,上的点,且.
求证:(1);
(2).
第二课时
一、判断题
1.一组邻边相等,且对角线互相垂直的四边形是菱形.( )
2.一条对角线平分一组对角的四边形是菱形.( )
3.对角线交点到各边中点的距离都相等的四边形是菱形.( )
4.菱形是轴对称图形,它的对称轴只有一条.( )
5.菱形的对角线互相垂直平分,且平分各内角.( )
二、填空题
6.菱形的邻角比为1:5,它的高为1.5cm,则它的周长为_______.
7.两条对角线_________的四边形是菱形.
8.已知菱形的两对角线的比为2:3,两对角线和为20, 则这对角线长分别为_____,_______.
9.菱形ABCD的AC交BD于O,AB=13,BO=12,AO=5,求菱形的周长=_____,面积= ____.
10.O为菱形ABCD的对角线交点,E、F、G、H分别是菱形各边的中点,若OE=3cm, 则OF=_____,OG=_______,OH=______.
三、选择题
11.从菱形的钝角的顶点向对边引垂线,并且这条垂线平分对边, 则该菱形的钝角为( ).
A.110° B.120° C.135° D.150°
12.菱形的两邻角之比为1:2,如果它的较短对角线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
13.菱形具有而矩形不一定具有的性质是( ).
A.对边相等 B.对角相等
C.对角线互相相等 D.对有线相等
14.能够找到一点使该点到各边距离相等的图形为( ).
A.平行四边形 B.菱形 C.矩形 D.不存在
15.下列说法不正确的是( ).
A.菱形的对角线互相垂直 B.菱形的对角线平分各内角
C.菱形的对角线相等 D.菱形的对角线交点到各边等距离
四、解答题
16.如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M.试说明M为AB的中点.
17.如图所示,已知菱形ABCD中E在BC上,且AB=AE,∠BAE=∠EAD,AE交BD于M,试说明BE=AM.
18.如图所示,已知在菱形ABCD中,AE⊥CD于E,∠ABC=60°,求∠CAE的度数.
19.如图所示,菱形的周长为20cm,两邻角的比为1:2.
求:(1)较短对角线长是多少?(2)一组对边的距离是多少?
20.如图所示,已知菱形ABCD中,E、F分别在BC和CD上,且∠B=∠EAF= 60°,∠BAE=15°,求∠CEF的度数.
21.已知:菱形一边及这边上的高.
求作:满足条件的这个菱形.
22.已知在菱形ABCD中,AE⊥BC于E,且BE=EC,若AC=6,求菱形ABCD的各边长.
23.菱形一边与两条对角线所构成的两个角的差为10°,求菱形的各内角.
24.如图所示,已知菱形ABCD中,E、F是BC、CD上的点,且AE=EF=AF=AB, 求∠C的度数.
25.如图所示,O为矩形ABCD的对角线交点,DE∥AC,CE⊥BD,OE与CD 互相垂直平分吗?请说明理由.
26.如图所示,已知在菱形ABCD中,E在BC上,若∠B=∠EAD=70°,ED 平分∠AEC吗?请说明理由.
第一课时参考答案
一、选择题
1. D 2. D 3. D4. B5. D6. C7. C8. D
9. C10. D11. A12. D13. B
二、填空题
14. 和
15.
16. 2.4
17. ,
18. 或
19. ,,,
20. 都相等,互相垂直平分,平分一组对角
21. 4
22. 4
23.
24. 相等
25.
26.
27.
28.
三、证明题
29. 提示:
30. (1)利用“边角边”可证;
(2),,.
第二课时参考答案
一、1.× 2.× 3.√ 4.× 5.√
二、6.12cm 7.互相垂直平分 8.8 12 9.52 120 10.3cm 3cm 3cm
三、11.B 12.C 13.C 14.B 15.C
四、16.由于△AME是以AC为轴的轴对称图形(其中∠1=∠2,ME⊥AC)
所以AM=AE=AD, 故AM=AB,所以M是AB的中点.
17.设∠BAE=x°,则∠EAD=2x°, 所以∠AEB=∠ABC=2x°,
那么5x°=180°,x=36°,由于∠1=∠2,故∠2=36°,∠BEM=72°,
那么∠BME=72°,所以∠BEM=∠BME即BE=BM,又∠1=∠5=36°,
所以BM=AM,那么BE=AM
18.30° 19.(1)20cm (2)10cm
20.连AC,可得△ABC为等边三角形,则∠ACF=120°-60°=60°,
由已知得∠2=∠1=15°,把△ABE绕着A按逆时针方向旋转60 °可与△ACF重合,这样AF=AE,由于∠EAF=60°,故△AEF为等边三角形,那么∠AEF=60°,由于∠AEB=180°-60°-15°=105°,故∠CEF=180°-60°-105°=15°
21.略 22.6 6 6 6 23.80° 100° 80° 100° 24.100°
25.四边形ODEC是菱形
26.由∠B=∠EAD=70°,AD∥BC,即∠AEB=70°,
那么∠1=40°,由AB=AE,AB=AD,得AE= AD,即∠2=55°,
而∠AEC=180°-70°=110°,故∠DEC=110°-55°=55°,
所以ED平分∠AEC
第一课时
一、选择题
1. 若菱形的一条对角线长是另一条对角线长的2倍,且此菱形的面积为,则它的边长是( )
A. B. C. D.
2. 如图,在菱形中,为的中点,作,交于点,如果,那么长为( )
A.10 B.4 C.6 D.8
3. 如图,在菱形中,,的垂直平分线交对角线于点,为垂足,连结,则等于( )
A. B. C. D.
4. 如图所示,在菱形中,,周长为,则较长的对角线长为( )
A. B. C. D.
5. 菱形中,若,的平分线与边间的关系是
( )
A.相等 B.互相平分但不垂直
C.互相垂直但不平分 D.垂直平分
6. 菱形周长为,两条对角线的差为,则该菱形面积为( )
A. B. C. D.
7. 若菱形周长52cm,一条对角线长24cm,则它的面积是( ).
A.60 B.80 C.120 D.40
8. 如图,菱形中,对角线相交于点,则下列性质:
①;
②,且;
③;
④,.
其中菱形一定具有的是( )
A.①②③ B.①②④ C.①③④ D.②③④
9. 菱形中,对角线与交于点,则下列说法不正确的是( )
A. B.
C. D.
10. 菱形具有而矩形不一定有的性质是( )
A.对边平行 B.对边相等
C.对角线互相平分 D.对角线互相垂直
11. 菱形的周长等于它的高的8倍,则它各个角是( )
A.和 B.和
C.和 D.和
12. 若菱形的一条对角线是另一条对角线长的2倍,且此菱形的面积为16,则它的边长为( )
A.4 B.2 C. D.
13. 菱形和矩形一定都具有的性质是( )
A.对角线相等. B.对角线互相平分.
C.对角线互相垂直. D.每条对角线平分一组对角.
二、填空题
14. 菱形周长为24cm,高为3cm,则菱形相邻两角的度数分别为 .
15. 已知菱形两条对角线之比为,它们的差为,则菱形的面积是________.
16. 如图,在菱形ABCD中,对角线AC=6,BD=8,则菱形的高为_______.
17. 已知菱形的周长为,两条对角线长的比为,则此菱形两条对角线的长分别为 .
18. 已知菱形的边长为6,,如果点是菱形内一点,且,那么的长为 .
19. 已知菱形的一条对角线长为4cm,周长为16cm,则菱形的四个角分别为 .
20. 菱形的四条边_________对角线__________且每一条对角线__________.
21. 菱形的两条对角线把菱形分割成一些三角形,其中直角三角形有_________个.
22. 菱形的对线交于点,则图中等腰三角形的个数是________个.
23. 已知菱形的周长为,两个相邻角之比为,则较短对角线长为__________.
24. 菱形中,点到边所在直线的距离 .
25. 在菱形中,交于,,,则菱形的周长为 .
26. 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是______.
27. 已知菱形的两条对角线的长都是8cm,则菱形的边长为 cm.
28. 在菱形ABCD中,AE、AF分别垂直平分边BC、CD,则∠EAF= .
三、证明题
29. 已知如图,在菱形中,于,于.请说明:.
30. 已知:如图,菱形中,,分别是,上的点,且.
求证:(1);
(2).
第二课时
一、判断题
1.一组邻边相等,且对角线互相垂直的四边形是菱形.( )
2.一条对角线平分一组对角的四边形是菱形.( )
3.对角线交点到各边中点的距离都相等的四边形是菱形.( )
4.菱形是轴对称图形,它的对称轴只有一条.( )
5.菱形的对角线互相垂直平分,且平分各内角.( )
二、填空题
6.菱形的邻角比为1:5,它的高为1.5cm,则它的周长为_______.
7.两条对角线_________的四边形是菱形.
8.已知菱形的两对角线的比为2:3,两对角线和为20, 则这对角线长分别为_____,_______.
9.菱形ABCD的AC交BD于O,AB=13,BO=12,AO=5,求菱形的周长=_____,面积= ____.
10.O为菱形ABCD的对角线交点,E、F、G、H分别是菱形各边的中点,若OE=3cm, 则OF=_____,OG=_______,OH=______.
三、选择题
11.从菱形的钝角的顶点向对边引垂线,并且这条垂线平分对边, 则该菱形的钝角为( ).
A.110° B.120° C.135° D.150°
12.菱形的两邻角之比为1:2,如果它的较短对角线为3cm,则它的周长为( ).
A.8cm B.9cm C.12cm D.15cm
13.菱形具有而矩形不一定具有的性质是( ).
A.对边相等 B.对角相等
C.对角线互相相等 D.对有线相等
14.能够找到一点使该点到各边距离相等的图形为( ).
A.平行四边形 B.菱形 C.矩形 D.不存在
15.下列说法不正确的是( ).
A.菱形的对角线互相垂直 B.菱形的对角线平分各内角
C.菱形的对角线相等 D.菱形的对角线交点到各边等距离
四、解答题
16.如图所示,已知E为菱形ABCD的边AD的中点,EF⊥AC于F交AB于M.试说明M为AB的中点.
17.如图所示,已知菱形ABCD中E在BC上,且AB=AE,∠BAE=∠EAD,AE交BD于M,试说明BE=AM.
18.如图所示,已知在菱形ABCD中,AE⊥CD于E,∠ABC=60°,求∠CAE的度数.
19.如图所示,菱形的周长为20cm,两邻角的比为1:2.
求:(1)较短对角线长是多少?(2)一组对边的距离是多少?
20.如图所示,已知菱形ABCD中,E、F分别在BC和CD上,且∠B=∠EAF= 60°,∠BAE=15°,求∠CEF的度数.
21.已知:菱形一边及这边上的高.
求作:满足条件的这个菱形.
22.已知在菱形ABCD中,AE⊥BC于E,且BE=EC,若AC=6,求菱形ABCD的各边长.
23.菱形一边与两条对角线所构成的两个角的差为10°,求菱形的各内角.
24.如图所示,已知菱形ABCD中,E、F是BC、CD上的点,且AE=EF=AF=AB, 求∠C的度数.
25.如图所示,O为矩形ABCD的对角线交点,DE∥AC,CE⊥BD,OE与CD 互相垂直平分吗?请说明理由.
26.如图所示,已知在菱形ABCD中,E在BC上,若∠B=∠EAD=70°,ED 平分∠AEC吗?请说明理由.
第一课时参考答案
一、选择题
1. D 2. D 3. D4. B5. D6. C7. C8. D
9. C10. D11. A12. D13. B
二、填空题
14. 和
15.
16. 2.4
17. ,
18. 或
19. ,,,
20. 都相等,互相垂直平分,平分一组对角
21. 4
22. 4
23.
24. 相等
25.
26.
27.
28.
三、证明题
29. 提示:
30. (1)利用“边角边”可证;
(2),,.
第二课时参考答案
一、1.× 2.× 3.√ 4.× 5.√
二、6.12cm 7.互相垂直平分 8.8 12 9.52 120 10.3cm 3cm 3cm
三、11.B 12.C 13.C 14.B 15.C
四、16.由于△AME是以AC为轴的轴对称图形(其中∠1=∠2,ME⊥AC)
所以AM=AE=AD, 故AM=AB,所以M是AB的中点.
17.设∠BAE=x°,则∠EAD=2x°, 所以∠AEB=∠ABC=2x°,
那么5x°=180°,x=36°,由于∠1=∠2,故∠2=36°,∠BEM=72°,
那么∠BME=72°,所以∠BEM=∠BME即BE=BM,又∠1=∠5=36°,
所以BM=AM,那么BE=AM
18.30° 19.(1)20cm (2)10cm
20.连AC,可得△ABC为等边三角形,则∠ACF=120°-60°=60°,
由已知得∠2=∠1=15°,把△ABE绕着A按逆时针方向旋转60 °可与△ACF重合,这样AF=AE,由于∠EAF=60°,故△AEF为等边三角形,那么∠AEF=60°,由于∠AEB=180°-60°-15°=105°,故∠CEF=180°-60°-105°=15°
21.略 22.6 6 6 6 23.80° 100° 80° 100° 24.100°
25.四边形ODEC是菱形
26.由∠B=∠EAD=70°,AD∥BC,即∠AEB=70°,
那么∠1=40°,由AB=AE,AB=AD,得AE= AD,即∠2=55°,
而∠AEC=180°-70°=110°,故∠DEC=110°-55°=55°,
所以ED平分∠AEC
