华师大版八年级数学下册试题一课一练20.3数据的离散程度习题1(Word版,含答案)
文档属性
| 名称 | 华师大版八年级数学下册试题一课一练20.3数据的离散程度习题1(Word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 00:00:00 | ||
图片预览



文档简介
20.3 数据的离散程度习题1
第一课时
一、选择题
1.若一组数据1,2,3,x的极差为6,则x的值是( )
A.7 B.8 C.9 D.7或-3
2.已知甲、乙两组数据的平均数相等,若甲组数据的方差=0.055,乙组数据的方差 =0.105,则( )
A.甲组数据比乙组数据波动大
B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大
D.甲.乙两组数据的数据波动不能比较
3.一组数据13,14,15,16,17的标准差是( )
A.0 B.10 C. D.2
4.在方差的计算公式s=[(x-20)+(x-20)+……+(x-20)]中,数字10和20分别表示的意义可以是( )
A.数据的个数和方差 B.平均数和数据的个数
C.数据的个数和平均数 D.数据组的方差和平均数
5.已知一组数据的方差为,数据为:-1,0,3,5,x,那么x等于( )
A.-2或5.5 B.2或-5.5 C.4或11 D.-4或-11
6.如果将所给定的数据组中的每个数都减去一个非零常数,那么该数组的 ( )
A.平均数改变,方差不变 B.平均数改变,方差改变
C.平均数不变,方差改变 D.平均数不变,方差不变
二、填空题
7.数据100,99,99,100,102,100的方差=_________.
8.已知一组数据-3,-2,1,3,6,x的中位数为1,则其方差为 .
9.已知数据:1,2,1,0,-1,-2,0,-1,这组数据的方差为__________.
10.已知一个样本的方差,则这个样本的容量是____________,样本的平均数是_____________.
11.若40个数据的平方和是56,平均数是,则这组数据的方差是_________
12.体育老师对甲.乙两名同学分别进行了5次立定跳远测试,经计算这两名同学成绩的平均数相同,甲同学成绩的方差是0.03,乙同学的成绩(单位:m)如下:2.3 2.2 2.5 2.1 2.4,那么这两名同学立定跳远成绩比较稳定的是____同学.
三、解答题
13.甲.乙两位同学五次数学测验成绩如下表:
测验(次) 1 2 3 4 5 平均数 方差
甲(分) 75 90 96 83 81
乙(分) 86 70 90 95 84
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩进行分析,并写出一条合理化建议.
14.一次期中考试中,A.B.C.D.E五位同学的数学.英语成绩等有关信息如下表所示:(单位:分)
A B C D E 平均分 标准差
数学 71 72 69 68 70
英语 88 82 94 85 76 85
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
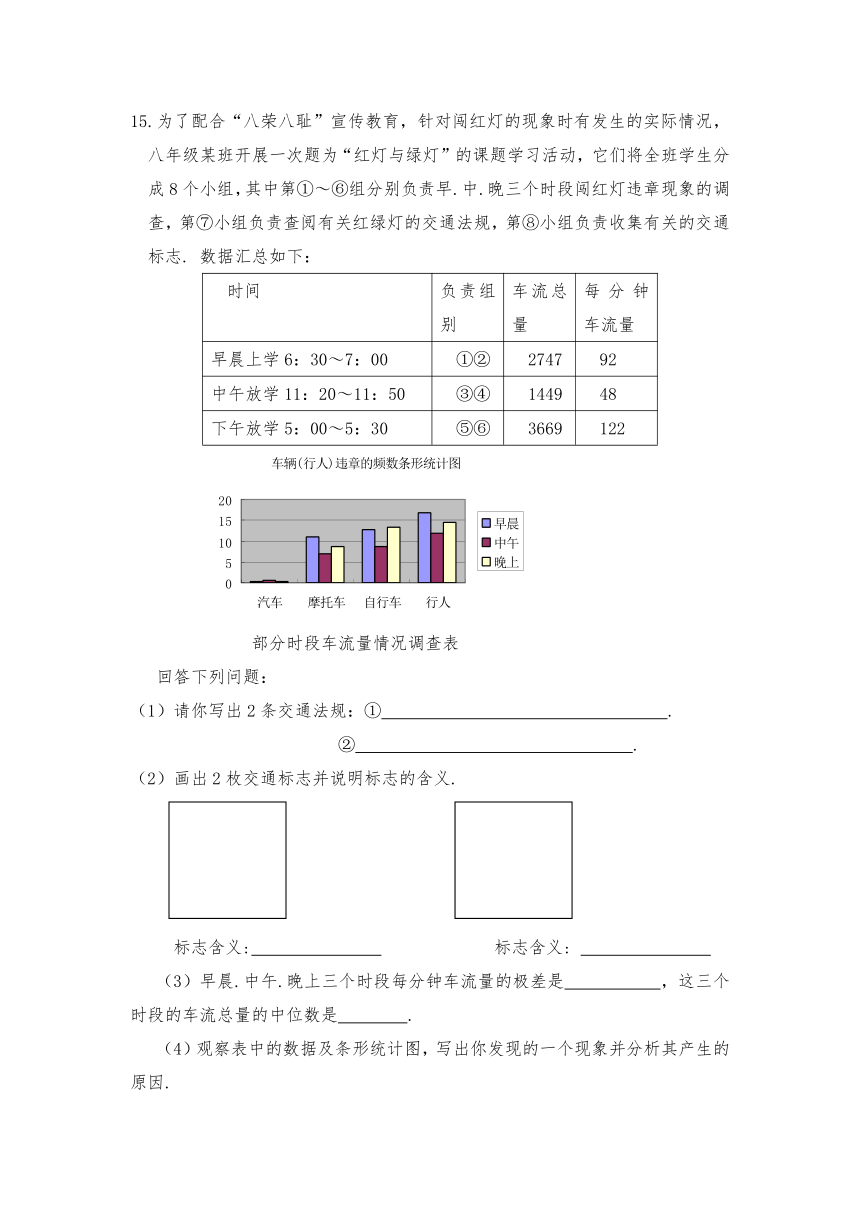
15.为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
时间 负责组别 车流总量 每分钟车流量
早晨上学6:30~7:00 ①② 2747 92
中午放学11:20~11:50 ③④ 1449 48
下午放学5:00~5:30 ⑤⑥ 3669 122
部分时段车流量情况调查表
回答下列问题:
(1)请你写出2条交通法规:① .
② .
(2)画出2枚交通标志并说明标志的含义.
标志含义: 标志含义:
(3)早晨.中午.晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 .
(4)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(5)通过分析写一条合理化建议.
16.为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
根据测试得到的有关数据,试解答下列问题:
(1) 考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些;
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
第二课时
一、选择题
1.如图是甲.乙两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( )
A.甲 B.乙 C.甲、乙的成绩一样稳定 D.无法确定
2.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机抽取甲.乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较S 2甲.S 2乙的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A.S 2甲>S 2乙 B.S 2甲=S 2乙 C.S 2甲<S 2乙 D.S 2甲≤S 2
3.人数相等的甲.乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
4.下列统计量中,能反映一名同学在7~9年级学段的学习成绩稳定程度的是( )
A.平均数 B.中位数 C.众数 D.方差
5.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,2,则在这10天中该车间生产零件的次品数的( )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
6.在甲.乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
二、填空题
7.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为__________cm.
8.五个数1,2,4,5,a的平均数是3,则a= ,这五个数的方差为 .
9.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 ,中位数为 ,方差为 .
10.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是____环,中位数_____环,方差是______环.
11.今天5月甲.乙两种股票连续10天开盘价格如下:(单位:元)
甲 5.23 5.28 5.35 5.3 5.28 5.2 5.08 5.31 5.44 5.46
乙 6.3 6.5 6.7 6.52 6.66 6.8 6.9 6.83 6.58 6.55
则在10天中,甲.乙两种股票波动较大的是 .
12.已知数据a.b.c的方差是1,则4a,4b,4c的方差是 .
三、解答题
13.某学生在一学年的6次测验中语文.数学成绩分别为(单位:分):
语文:80,84,88,76,79,85
数学:80,75,90,64,88,95
试估计该学生是数学成绩稳定还是语文成绩稳定?
14.在某次体育活动中,统计甲.乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
班 级 参加人数 平均次数 中位 数 方 差
甲 班 55 135 149 190
乙 班 55 135 151 110
下面有三种说法:(1)甲班学生的平均成绩高于乙班的学生的平均成绩;(2)甲班学生成绩的波动比乙班成绩的波动大;(3)甲班学生成绩优秀的人数比乙班学生成绩优秀的人数(跳绳次数≥150次为优秀)少,试判断上述三个说法是否正确?请说明理由.
15.某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
根据上表解答下列问题:
(1)完成下表:
姓名 极差(分) 平均成绩(分) 中位数(分) 众数(分) 方差
小王 40 80 75 75 190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王.小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
第一课时参考答案
1.D 2.B 3.C 4.C 5.A 6.A
7.1 8.9 9.1.5 10.11 6 11.0.9 12.乙
13.解:
平均分 方差
甲 85 53.2
乙 85 70.4
从上述数据可以看出,两人的成绩的平均分相等,乙同学的数学成绩不够稳定,波动较大,希望乙同学在学习上补缺补漏,稳定自己的成绩
14.(1)数学平均分为70分,英语标准差为6
(2)数学:(71-70)÷=,英语(88-85)÷6=0.5
∵>0.5,∴数学成绩考得更好些
15.(1)如:红灯停.绿灯行;过马路要走人行横道线;不可酒后驾车等.
(2)略;(3)74 2747;
(4)现象:如行人违章率最高,汽车违章率低,原因是汽车驾驶员是经过专门培训过的,行人存在图方便的心理等.
16.(1)B (2)B(3)B呈现上升趋势
第二课时参考答案
1.A 2.A 3.B 4.D 5.D 6.B
7.4
8.3 2
9.0 0
10.8 8 2
11.乙
12.16
13.语文平均分为82分,数学的平均分为82分,语文的极差为12分,数学的极差为31分,从极差上看,该同学语文成绩相对稳定些,当然也可通过求方差来判别.
14.从表中可以看出,甲班学生平均成绩为135,乙班学生平均成绩也是135,因而甲.乙两班平均成绩相同,所以(1)的说法是错误的;因s=190> s=110,故甲的波动比乙大,所以(2)的说法是正确的;从中位数上看,甲班学生跳绳次数有27人少于149次,27人大于149次,而乙班学生跳绳次数151次的必有27人,故必有至少28人跳绳次数高于150次,因而甲班学生成绩的优秀人数比乙班少,从而知(3)是正确的.
15.(1)极差:90-70=20
平均成绩:(70+90+80+80+80)÷5=80
中位数:将这组数据按从小到大的顺序排列:70.80.80.80.90,就会得到中位数是80.
众数:在这组数据中80出现了3次,出现次数最多,因此这组数据的众数是80
方差:=40
(2)在这五次考试中,成绩比较稳定的是小李,小王的优秀率为40%,小李的优秀率为80%
(3)方案一:我选小李去参加比赛,因为小李的优秀率高,有4次得80分,成绩比较稳定,获奖机会大
方案二:我选小王去参加比赛,因为小王的成绩获得一等奖的机率较高,有2次90分以上(含90分)因此有可能获得一等奖.
第一课时
一、选择题
1.若一组数据1,2,3,x的极差为6,则x的值是( )
A.7 B.8 C.9 D.7或-3
2.已知甲、乙两组数据的平均数相等,若甲组数据的方差=0.055,乙组数据的方差 =0.105,则( )
A.甲组数据比乙组数据波动大
B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大
D.甲.乙两组数据的数据波动不能比较
3.一组数据13,14,15,16,17的标准差是( )
A.0 B.10 C. D.2
4.在方差的计算公式s=[(x-20)+(x-20)+……+(x-20)]中,数字10和20分别表示的意义可以是( )
A.数据的个数和方差 B.平均数和数据的个数
C.数据的个数和平均数 D.数据组的方差和平均数
5.已知一组数据的方差为,数据为:-1,0,3,5,x,那么x等于( )
A.-2或5.5 B.2或-5.5 C.4或11 D.-4或-11
6.如果将所给定的数据组中的每个数都减去一个非零常数,那么该数组的 ( )
A.平均数改变,方差不变 B.平均数改变,方差改变
C.平均数不变,方差改变 D.平均数不变,方差不变
二、填空题
7.数据100,99,99,100,102,100的方差=_________.
8.已知一组数据-3,-2,1,3,6,x的中位数为1,则其方差为 .
9.已知数据:1,2,1,0,-1,-2,0,-1,这组数据的方差为__________.
10.已知一个样本的方差,则这个样本的容量是____________,样本的平均数是_____________.
11.若40个数据的平方和是56,平均数是,则这组数据的方差是_________
12.体育老师对甲.乙两名同学分别进行了5次立定跳远测试,经计算这两名同学成绩的平均数相同,甲同学成绩的方差是0.03,乙同学的成绩(单位:m)如下:2.3 2.2 2.5 2.1 2.4,那么这两名同学立定跳远成绩比较稳定的是____同学.
三、解答题
13.甲.乙两位同学五次数学测验成绩如下表:
测验(次) 1 2 3 4 5 平均数 方差
甲(分) 75 90 96 83 81
乙(分) 86 70 90 95 84
请你在表中的空白处填上适当的数,用学到的统计知识对两位同学的成绩进行分析,并写出一条合理化建议.
14.一次期中考试中,A.B.C.D.E五位同学的数学.英语成绩等有关信息如下表所示:(单位:分)
A B C D E 平均分 标准差
数学 71 72 69 68 70
英语 88 82 94 85 76 85
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差.
从标准分看,标准分大的考试成绩更好.请问A同学在本次考试中,数学与英语哪个学科考得更好?
15.为了配合“八荣八耻”宣传教育,针对闯红灯的现象时有发生的实际情况,八年级某班开展一次题为“红灯与绿灯”的课题学习活动,它们将全班学生分成8个小组,其中第①~⑥组分别负责早.中.晚三个时段闯红灯违章现象的调查,第⑦小组负责查阅有关红绿灯的交通法规,第⑧小组负责收集有关的交通标志. 数据汇总如下:
时间 负责组别 车流总量 每分钟车流量
早晨上学6:30~7:00 ①② 2747 92
中午放学11:20~11:50 ③④ 1449 48
下午放学5:00~5:30 ⑤⑥ 3669 122
部分时段车流量情况调查表
回答下列问题:
(1)请你写出2条交通法规:① .
② .
(2)画出2枚交通标志并说明标志的含义.
标志含义: 标志含义:
(3)早晨.中午.晚上三个时段每分钟车流量的极差是 ,这三个时段的车流总量的中位数是 .
(4)观察表中的数据及条形统计图,写出你发现的一个现象并分析其产生的原因.
(5)通过分析写一条合理化建议.
16.为选派一名学生参加全市实践活动技能竞赛,A.B两位同学在学校实习基地现场进行加工直径为20mm的零件的测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)
根据测试得到的有关数据,试解答下列问题:
(1) 考虑平均数与完全符合要求的个数,你认为哪个同学的成绩好些;
(2)计算出SB2的大小,考虑平均数与方差,说明谁的成绩好些;
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.
平均数 方差 完全符合要求个数
A 20 0.026 2
B 20 SB2
第二课时
一、选择题
1.如图是甲.乙两位同学5次数学考试成绩的折线统计图,你认为成绩较稳定的是( )
A.甲 B.乙 C.甲、乙的成绩一样稳定 D.无法确定
2.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机抽取甲.乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较S 2甲.S 2乙的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A.S 2甲>S 2乙 B.S 2甲=S 2乙 C.S 2甲<S 2乙 D.S 2甲≤S 2
3.人数相等的甲.乙两班学生参加了同一次数学测验,班级平均分和方差如下: =80,=80,s=240,s =180,则成绩较为稳定的班级为( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
4.下列统计量中,能反映一名同学在7~9年级学段的学习成绩稳定程度的是( )
A.平均数 B.中位数 C.众数 D.方差
5.某车间6月上旬生产零件的次品数如下(单位:个):0,2,0,2,3,0,2,3,1,2,则在这10天中该车间生产零件的次品数的( )
A.众数是4 B.中位数是1.5 C.平均数是2 D.方差是1.25
6.在甲.乙两块试验田内,对生长的禾苗高度进行测量,分析数据得:甲试验田内禾苗高度数据的方差比乙实验田的方差小,则( )
A.甲试验田禾苗平均高度较高 B.甲试验田禾苗长得较整齐
C.乙试验田禾苗平均高度较高 D.乙试验田禾苗长得较整齐
二、填空题
7.5名同学目测同一本教科书的宽度时,产生的误差如下(单位:cm):0,2,-2,-1,1,则这组数据的极差为__________cm.
8.五个数1,2,4,5,a的平均数是3,则a= ,这五个数的方差为 .
9.已知一组数据1,2,1,0,-1,-2,0,-1,则这组数据的平均数为 ,中位数为 ,方差为 .
10.某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9,则这五次射击的平均成绩是____环,中位数_____环,方差是______环.
11.今天5月甲.乙两种股票连续10天开盘价格如下:(单位:元)
甲 5.23 5.28 5.35 5.3 5.28 5.2 5.08 5.31 5.44 5.46
乙 6.3 6.5 6.7 6.52 6.66 6.8 6.9 6.83 6.58 6.55
则在10天中,甲.乙两种股票波动较大的是 .
12.已知数据a.b.c的方差是1,则4a,4b,4c的方差是 .
三、解答题
13.某学生在一学年的6次测验中语文.数学成绩分别为(单位:分):
语文:80,84,88,76,79,85
数学:80,75,90,64,88,95
试估计该学生是数学成绩稳定还是语文成绩稳定?
14.在某次体育活动中,统计甲.乙两班学生每分钟跳绳的成绩(单位:次)情况如下表:
班 级 参加人数 平均次数 中位 数 方 差
甲 班 55 135 149 190
乙 班 55 135 151 110
下面有三种说法:(1)甲班学生的平均成绩高于乙班的学生的平均成绩;(2)甲班学生成绩的波动比乙班成绩的波动大;(3)甲班学生成绩优秀的人数比乙班学生成绩优秀的人数(跳绳次数≥150次为优秀)少,试判断上述三个说法是否正确?请说明理由.
15.某校要从小王和小李两名同学中挑选一人参加全国数学竞赛,在最近的五次选拔测试中,他俩的成绩分别如下表:
根据上表解答下列问题:
(1)完成下表:
姓名 极差(分) 平均成绩(分) 中位数(分) 众数(分) 方差
小王 40 80 75 75 190
小李
(2)在这五次测试中,成绩比较稳定的同学是谁?若将80分以上(含80分)的成绩视为优秀,则小王.小李在这五次测试中的优秀率各是多少?
(3)历届比赛表明,成绩达到80分以上(含80分)就很可能获奖,成绩达到90分以上(含90分)就很可能获得一等奖,那么你认为应选谁参加比赛比较合适?说明你的理由.
第一课时参考答案
1.D 2.B 3.C 4.C 5.A 6.A
7.1 8.9 9.1.5 10.11 6 11.0.9 12.乙
13.解:
平均分 方差
甲 85 53.2
乙 85 70.4
从上述数据可以看出,两人的成绩的平均分相等,乙同学的数学成绩不够稳定,波动较大,希望乙同学在学习上补缺补漏,稳定自己的成绩
14.(1)数学平均分为70分,英语标准差为6
(2)数学:(71-70)÷=,英语(88-85)÷6=0.5
∵>0.5,∴数学成绩考得更好些
15.(1)如:红灯停.绿灯行;过马路要走人行横道线;不可酒后驾车等.
(2)略;(3)74 2747;
(4)现象:如行人违章率最高,汽车违章率低,原因是汽车驾驶员是经过专门培训过的,行人存在图方便的心理等.
16.(1)B (2)B(3)B呈现上升趋势
第二课时参考答案
1.A 2.A 3.B 4.D 5.D 6.B
7.4
8.3 2
9.0 0
10.8 8 2
11.乙
12.16
13.语文平均分为82分,数学的平均分为82分,语文的极差为12分,数学的极差为31分,从极差上看,该同学语文成绩相对稳定些,当然也可通过求方差来判别.
14.从表中可以看出,甲班学生平均成绩为135,乙班学生平均成绩也是135,因而甲.乙两班平均成绩相同,所以(1)的说法是错误的;因s=190> s=110,故甲的波动比乙大,所以(2)的说法是正确的;从中位数上看,甲班学生跳绳次数有27人少于149次,27人大于149次,而乙班学生跳绳次数151次的必有27人,故必有至少28人跳绳次数高于150次,因而甲班学生成绩的优秀人数比乙班少,从而知(3)是正确的.
15.(1)极差:90-70=20
平均成绩:(70+90+80+80+80)÷5=80
中位数:将这组数据按从小到大的顺序排列:70.80.80.80.90,就会得到中位数是80.
众数:在这组数据中80出现了3次,出现次数最多,因此这组数据的众数是80
方差:=40
(2)在这五次考试中,成绩比较稳定的是小李,小王的优秀率为40%,小李的优秀率为80%
(3)方案一:我选小李去参加比赛,因为小李的优秀率高,有4次得80分,成绩比较稳定,获奖机会大
方案二:我选小王去参加比赛,因为小王的成绩获得一等奖的机率较高,有2次90分以上(含90分)因此有可能获得一等奖.
