2021-2022学年苏科版七年级数学下册9.4乘法公式 同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册9.4乘法公式 同步练习题 (word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览



文档简介
2021-2022学年苏科版七年级数学下册《9-4乘法公式》同步练习题(附答案)
一.选择题
1.下列多项式的乘法中能用平方差公式计算的是( )
A.(a+3)(a+4) B.(m﹣2n)(﹣m﹣2n)
C.(p+5)(p+5) D.(3a﹣4b)(4a+3b)
2.若a2﹣b2=10,a﹣b=2,则a+b的值为( )
A.5 B.2 C.10 D.无法计算
3.化简(2+1)(22+1)(24+1)(28+1)(216+1)的结果是( )
A.232﹣1 B.232+1 C.(216+1)2 D.(216﹣1)2
4.若a+b=﹣3,ab=﹣10,则a﹣b的值是( )
A.0或7 B.0或﹣13 C.﹣7或7 D.﹣13或13
5.若a+b=6,ab=4,则a2+4ab+b2的值为( )
A.40 B.44 C.48 D.52
6.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
7.若a=2020×2021+1,b=20202﹣2020×2021+20212,在下列判断结果正确的是( )
A.a<b B.a=b C.a>b D.无法判断
8.已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
9.用4个长为a,宽为b的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)(a﹣b)=a2﹣b2 D.(a+b)2﹣(a﹣b)2=4ab
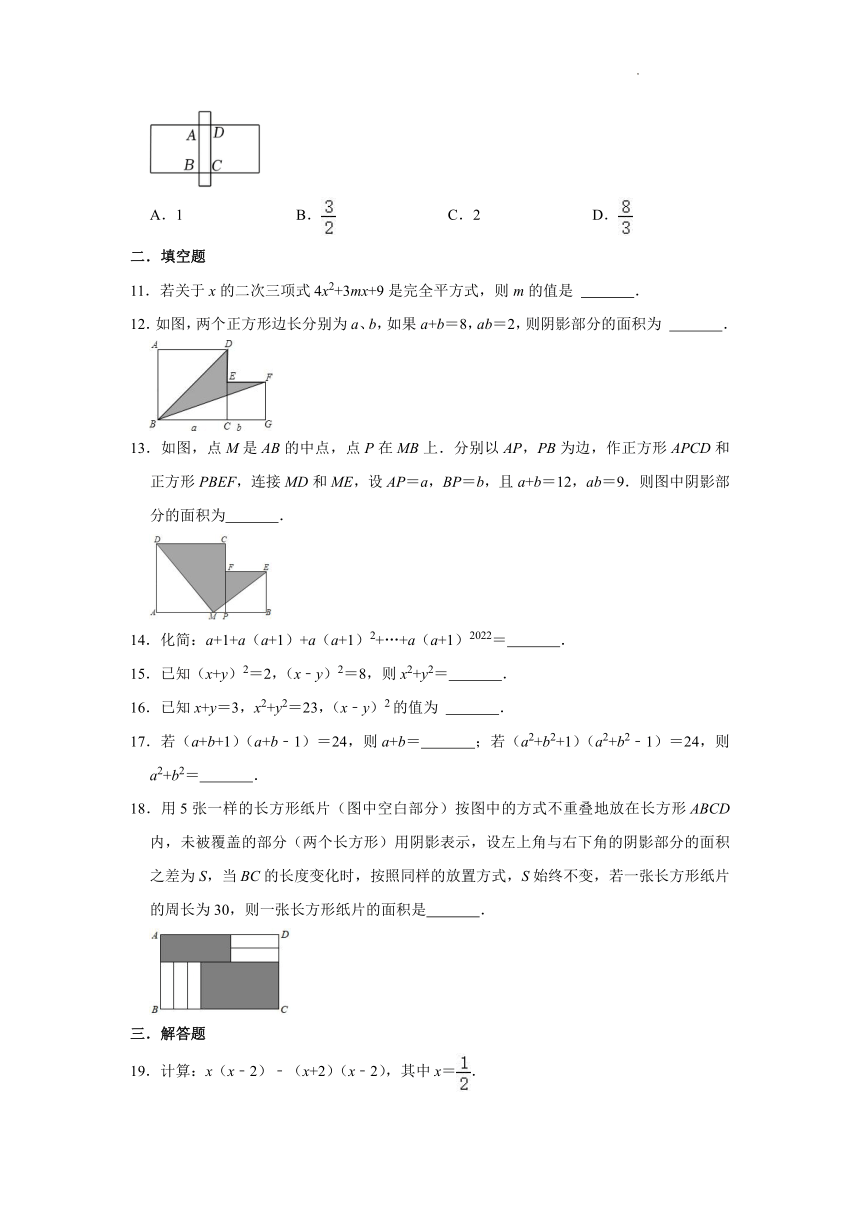
10.某中学开展“筑梦冰雪,相约冬奥”的学科活动,设计几何图形作品表达对冬奥会的祝福.小冬以长方形ABCD的四条边为边向外作四个正方形,设计出“中”字图案,如图所示.若四个正方形的周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.1 B. C.2 D.
二.填空题
11.若关于x的二次三项式4x2+3mx+9是完全平方式,则m的值是 .
12.如图,两个正方形边长分别为a、b,如果a+b=8,ab=2,则阴影部分的面积为 .
13.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME,设AP=a,BP=b,且a+b=12,ab=9.则图中阴影部分的面积为 .
14.化简:a+1+a(a+1)+a(a+1)2+…+a(a+1)2022= .
15.已知(x+y)2=2,(x﹣y)2=8,则x2+y2= .
16.已知x+y=3,x2+y2=23,(x﹣y)2的值为 .
17.若(a+b+1)(a+b﹣1)=24,则a+b= ;若(a2+b2+1)(a2+b2﹣1)=24,则a2+b2= .
18.用5张一样的长方形纸片(图中空白部分)按图中的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终不变,若一张长方形纸片的周长为30,则一张长方形纸片的面积是 .
三.解答题
19.计算:x(x﹣2)﹣(x+2)(x﹣2),其中x=.
20.计算:(x﹣2y+3)(x+2y﹣3).
21.计算:.
22.已知a+b=5,ab=.
(1)求a2+b2的值;
(2)求a﹣b的值.
23.化简求值:
(2a﹣b)2﹣(a﹣2b)(a+2b)+(6a2b+8ab2)÷2b,其中a=2,b=﹣1.
24.化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
25.运用乘法公式计算:
(1)(2x+3y)2(2x﹣3y)2;
(2)(x+1)(x﹣1)(x2+1)(x4+1).
26.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
27.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.比如:用图1所示的正方形与长方形纸片,可以拼成一个图2所示的正方形.
请你解决下列问题:
(1)利用不同的代数式表示:图2中阴影部分的面积S,写出你从中获得的等式,并加以证明;
(2)已知(2022﹣m)(2019﹣m)=3505,请用(1)中的结论,求(2022﹣m)2+(2019﹣m)2的值.
28.探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是 (用式子表示),即乘法公式中的 公式.
(2)运用你所得到的公式计算:
①10.3×9.7;
②(x+2y﹣3z)(x﹣2y﹣3z).
29.用1张边长为a的正方形纸片,1张边长为b的正方形纸片,2张长和宽分别为a,b的长方形纸片拼成如图1所示的大正方形.
(1)观察图1,试用两种不同的方法表示图1中两个阴影图形面积的和(用含a,b的代数式表示).
代数式1: ;
代数式2: ;
(2)从(1)中你能发现什么结论?请用等式表示出来: ;
(3)利用(2)中得出的结论解决下面的问题:
①若a+b=4,a2+b2=10,则ab的值为: ;
②如图2,点C是线段AB上的一点,以AC,BC为边向两边作正方形ACDE与正方形CFGB,若AB=7,两正方形的面积和为S1+S2=25.图中阴影部分的面积为 .
参考答案
一.选择题
1.解:平方差公式:(a+b)(a﹣b)=a2﹣b2,
(m﹣2n)(﹣m﹣2n)=(﹣2n+m)(﹣2n﹣m)=4n2﹣m2,
故选:B.
2.解:∵a2﹣b2=10,
∴(a+b)(a﹣b)=10,
∵a﹣b=2,
∴a+b=5.
故选:A.
3.解:(2+1)(22+1)(24+1)(28+1)(216+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)
=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1,
故选:A.
4.解:∵(a﹣b)2=(a+b)2﹣4ab,
∴(a﹣b)2=(﹣3)2﹣4×(﹣10)=49,
∴a﹣b=±7.
故选:C.
5.解:∵a+b=6,ab=4,
∴原式=(a+b)2+2ab=36+8=44,
故选:B.
6.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
7.解:a=2020×2021+1,
b=20202﹣2020×2021+20212
=(2020﹣2021)2+2020×2021
=2020×2021+1,
故a=b.
故选:B.
8.解:已知等式化简得:
(m+n)2=m2+n2+2mn=18①,
(m﹣n)2=m2+n2﹣2mn=2②,
由①+②得:2(m2+n2)=20,
则m2+n2=10.
故选:B.
9.解:∵此题阴影部分面积可表示为:(a+b)2﹣(a﹣b)2和4ab,
∴可得等式(a+b)2﹣(a﹣b)2=4ab,
故选:D.
10.解:设AB=a,BC=b,由四个正方形的周长之和为24,面积之和为12可得,
4a×2+4b×2=24,2a2+2b2=12,
即a+b=3①,a2+b2=6②,
由①得,a2+2ab+b2=9③,
③﹣②得2ab=3,
所以ab=,
即长方形ABCD的面积为,
故选:B.
二.填空题
11.解:∵4x2+3mx+9=(2x)2+3mx+32=(2x±3)2,
∴3m=2×2×3或3m=2×2×(﹣3),
∴m=±4,
故答案为:±4.
12.解:由题意得阴影部分面积为,
a +b ﹣﹣=﹣+=(a ﹣ab+b )=[(a+b) ﹣3ab],
∴当a+b=8,ab=2时,
阴影部分面积为,
(8 ﹣3×2)=×58=29,
故答案为:29.
13.解:AP=a,BP=b,
∴AB=a+b,
S正方形APCD=a2,
S正方形PBEF=b2,
又∵点M是AB的中点,a+b=12,
∴AM=BM===6,
∴S△DAM= AM AD= 6 a=3a,
S△MBE= BM BE= 6 b=3b,
∴S阴影面积=(S正方形APCD+S正方形PBEF)﹣(S△DAM+S△MBE)
=(a2+b2)﹣(3a+3b)
=(a2+b2)﹣3(a+b),
∵a+b=12,
∴(a+b)2=144,
∴a2+b2=(a+b)2﹣2ab=144﹣2×9=126,
∴(a2+b2)﹣3(a+b)
=126﹣3×12
=90.
故答案为:90.
14.解:原式=(a+1)2+a(a+1)2+…+a(a+1)2022
=(a+1)3+…+a(a+1)2022
=(a+1)2023
故答案为:(a+1)2023
15.解:∵(x+y)2=2,(x﹣y)2=8,
∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,
①+②得:2(x2+y2)=10,
∴x2+y2=5.
故答案为:5.
16.解:∵x+y=3,x2+y2=23,
∴2xy=(x+y)2﹣(x2+y2)=32﹣23=﹣14,
∴xy=﹣7;
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×(﹣7)=37.
故答案为:37.
17.解:∵(a+b+1)(a+b﹣1)=24,
∴[(a+b)+1][(a+b)﹣1]=24,
∴(a+b)2﹣1=24,
∴(a+b)2=25,
∴a+b=±5,
∵(a2+b2+1)(a2+b2﹣1)=24,
∴[(a2+b2)+1][(a2+b2)﹣1]=24,
∴(a2+b2)2﹣1=24,
∴(a2+b2)2=25,
∵a2≥0,b2≥0,
∴a2+b2≥0,
∴a2+b2=5,
故答案为:±5,5.
18.解:设一张长方形纸片的长为x,宽为y,长方形ABCD的长AD为a,宽AB为b,
S=2y(a﹣2x)﹣x(a﹣3y)=a(2y﹣x)+xy,
∵当BC的长度变化时,按照同样的放置方式,S始终不变,
∴2y﹣x=0,
∴x=2y,
∵一张长方形纸片的周长为30,
∴(x+y)×2=30,
∴x+y=15,
∴2y+y=15,
解得y=5,
∴x=10,
∴一张长方形纸片的面积是xy=10×5=50,
故答案为:50.
三.解答题
19.解:原式=x2﹣2x﹣(x2﹣4)
=x2﹣2x﹣x2+4
=﹣2x+4,
当x=时,原式=﹣1+4=3.
20.解:原式=x2﹣(2y﹣3)2
=x2﹣(4y2﹣12y+9)
=x2﹣4y2+12y﹣9.
21.解:原式=
=
=2022.
22.解:(1)∵a+b=5,ab=,
∴(a+b)2=25,
∴a2+2ab+b2=25,
∴a2+b2=25﹣2ab=25﹣=;
(2)∵a2+b2=,ab=,
∴a2+b2﹣2ab=16,
∴(a﹣b)2=16,
∴a﹣b=±4.
23.解:(2a﹣b)2﹣(a﹣2b)(a+2b)+(6a2b+8ab2)÷2b
=4a2﹣4ab+b2﹣a2+4b2+3a2+4ab
=6a2+5b2,
当a=2,b=﹣1时,原式=6a2+5b2
=6×22+5×(﹣1)2
=6×4+5×1
=24+5
=29.
24.解:原式=a2﹣4ab+4b2﹣(b+2a)(b﹣2a)﹣4a2+4ab
=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab
=a2+3b2.
25.解:(1)原式=(4x2﹣9y2)2
=16x4﹣72x2y2+81y4;
(2)原式=(x2﹣1)(x2+1)(x4+1)
=(x4﹣1)(x4+1)
=x8﹣1.
26.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
27.解:(1)图②中,S阴影=a2+b2,还可以表示为:S阴影=(a+b)2﹣2ab.
∴a2+b2=(a+b)2﹣2ab.
(2)设a=2022﹣m,b=2019﹣m,
则ab=3505,a﹣b=3.
∴(2022﹣m)2+(2019﹣m)2=a2+b2
=(a﹣b)2+2ab
=9+7010
=7019.
28.解:(1)(a+b)(a﹣b)=a2﹣b2;
故答案为(a+b)(a﹣b)=a2﹣b2,平方差.
(2)①原式=(10+0.3)(10﹣0.3)=102﹣0.32=100﹣0.09=99.91;
②原式=(x﹣3z)2﹣(2y)2=x2﹣6xz+9z2﹣4y2.
29.解:(1)由题意可得,图1中两个阴影图形面积的和为a2+b2或(a+b)2﹣2ab;
故答案应为:(1)a2+b2,a2+2ab+b2;
(2)从(1)中结论可得a2+b2=(a+b)2﹣2ab.
故答案应为:a2+b2=(a+b)2﹣2ab;
(3)①由a2+b2=(a+b)2﹣2ab可得,
2ab=(a+b)2﹣(a2+b2)
∴ab=,
∴当a+b=4,a2+b2=10时,
ab==3.
②由①得ab=,
=
=12,
可得
=
=6.
故答案应为:①3,②6.
一.选择题
1.下列多项式的乘法中能用平方差公式计算的是( )
A.(a+3)(a+4) B.(m﹣2n)(﹣m﹣2n)
C.(p+5)(p+5) D.(3a﹣4b)(4a+3b)
2.若a2﹣b2=10,a﹣b=2,则a+b的值为( )
A.5 B.2 C.10 D.无法计算
3.化简(2+1)(22+1)(24+1)(28+1)(216+1)的结果是( )
A.232﹣1 B.232+1 C.(216+1)2 D.(216﹣1)2
4.若a+b=﹣3,ab=﹣10,则a﹣b的值是( )
A.0或7 B.0或﹣13 C.﹣7或7 D.﹣13或13
5.若a+b=6,ab=4,则a2+4ab+b2的值为( )
A.40 B.44 C.48 D.52
6.若x+4=2y,则代数式x2﹣4xy+4y2的值为( )
A.6 B.8 C.12 D.16
7.若a=2020×2021+1,b=20202﹣2020×2021+20212,在下列判断结果正确的是( )
A.a<b B.a=b C.a>b D.无法判断
8.已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=( )
A.20 B.10 C.16 D.8
9.用4个长为a,宽为b的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( )
A.(a+b)2=a2+2ab+b2 B.(a﹣b)2=a2﹣2ab+b2
C.(a+b)(a﹣b)=a2﹣b2 D.(a+b)2﹣(a﹣b)2=4ab
10.某中学开展“筑梦冰雪,相约冬奥”的学科活动,设计几何图形作品表达对冬奥会的祝福.小冬以长方形ABCD的四条边为边向外作四个正方形,设计出“中”字图案,如图所示.若四个正方形的周长之和为24,面积之和为12,则长方形ABCD的面积为( )
A.1 B. C.2 D.
二.填空题
11.若关于x的二次三项式4x2+3mx+9是完全平方式,则m的值是 .
12.如图,两个正方形边长分别为a、b,如果a+b=8,ab=2,则阴影部分的面积为 .
13.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME,设AP=a,BP=b,且a+b=12,ab=9.则图中阴影部分的面积为 .
14.化简:a+1+a(a+1)+a(a+1)2+…+a(a+1)2022= .
15.已知(x+y)2=2,(x﹣y)2=8,则x2+y2= .
16.已知x+y=3,x2+y2=23,(x﹣y)2的值为 .
17.若(a+b+1)(a+b﹣1)=24,则a+b= ;若(a2+b2+1)(a2+b2﹣1)=24,则a2+b2= .
18.用5张一样的长方形纸片(图中空白部分)按图中的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终不变,若一张长方形纸片的周长为30,则一张长方形纸片的面积是 .
三.解答题
19.计算:x(x﹣2)﹣(x+2)(x﹣2),其中x=.
20.计算:(x﹣2y+3)(x+2y﹣3).
21.计算:.
22.已知a+b=5,ab=.
(1)求a2+b2的值;
(2)求a﹣b的值.
23.化简求值:
(2a﹣b)2﹣(a﹣2b)(a+2b)+(6a2b+8ab2)÷2b,其中a=2,b=﹣1.
24.化简:(a﹣2b)2﹣(2a+b)(b﹣2a)﹣4a(a﹣b).
25.运用乘法公式计算:
(1)(2x+3y)2(2x﹣3y)2;
(2)(x+1)(x﹣1)(x2+1)(x4+1).
26.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
27.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙的解决一些图形问题.比如:用图1所示的正方形与长方形纸片,可以拼成一个图2所示的正方形.
请你解决下列问题:
(1)利用不同的代数式表示:图2中阴影部分的面积S,写出你从中获得的等式,并加以证明;
(2)已知(2022﹣m)(2019﹣m)=3505,请用(1)中的结论,求(2022﹣m)2+(2019﹣m)2的值.
28.探究下面的问题:
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是 (用式子表示),即乘法公式中的 公式.
(2)运用你所得到的公式计算:
①10.3×9.7;
②(x+2y﹣3z)(x﹣2y﹣3z).
29.用1张边长为a的正方形纸片,1张边长为b的正方形纸片,2张长和宽分别为a,b的长方形纸片拼成如图1所示的大正方形.
(1)观察图1,试用两种不同的方法表示图1中两个阴影图形面积的和(用含a,b的代数式表示).
代数式1: ;
代数式2: ;
(2)从(1)中你能发现什么结论?请用等式表示出来: ;
(3)利用(2)中得出的结论解决下面的问题:
①若a+b=4,a2+b2=10,则ab的值为: ;
②如图2,点C是线段AB上的一点,以AC,BC为边向两边作正方形ACDE与正方形CFGB,若AB=7,两正方形的面积和为S1+S2=25.图中阴影部分的面积为 .
参考答案
一.选择题
1.解:平方差公式:(a+b)(a﹣b)=a2﹣b2,
(m﹣2n)(﹣m﹣2n)=(﹣2n+m)(﹣2n﹣m)=4n2﹣m2,
故选:B.
2.解:∵a2﹣b2=10,
∴(a+b)(a﹣b)=10,
∵a﹣b=2,
∴a+b=5.
故选:A.
3.解:(2+1)(22+1)(24+1)(28+1)(216+1)
=(2﹣1)(2+1)(22+1)(24+1)(28+1)(216+1)
=(22﹣1)(22+1)(24+1)(28+1)(216+1)
=(24﹣1)(24+1)(28+1)(216+1)
=(28﹣1)(28+1)(216+1)
=(216﹣1)(216+1)
=232﹣1,
故选:A.
4.解:∵(a﹣b)2=(a+b)2﹣4ab,
∴(a﹣b)2=(﹣3)2﹣4×(﹣10)=49,
∴a﹣b=±7.
故选:C.
5.解:∵a+b=6,ab=4,
∴原式=(a+b)2+2ab=36+8=44,
故选:B.
6.解:∵x+4=2y,
∴x﹣2y=﹣4,
∴x2﹣4xy+4y2=(x﹣2y)2=(﹣4)2=16.
故选:D.
7.解:a=2020×2021+1,
b=20202﹣2020×2021+20212
=(2020﹣2021)2+2020×2021
=2020×2021+1,
故a=b.
故选:B.
8.解:已知等式化简得:
(m+n)2=m2+n2+2mn=18①,
(m﹣n)2=m2+n2﹣2mn=2②,
由①+②得:2(m2+n2)=20,
则m2+n2=10.
故选:B.
9.解:∵此题阴影部分面积可表示为:(a+b)2﹣(a﹣b)2和4ab,
∴可得等式(a+b)2﹣(a﹣b)2=4ab,
故选:D.
10.解:设AB=a,BC=b,由四个正方形的周长之和为24,面积之和为12可得,
4a×2+4b×2=24,2a2+2b2=12,
即a+b=3①,a2+b2=6②,
由①得,a2+2ab+b2=9③,
③﹣②得2ab=3,
所以ab=,
即长方形ABCD的面积为,
故选:B.
二.填空题
11.解:∵4x2+3mx+9=(2x)2+3mx+32=(2x±3)2,
∴3m=2×2×3或3m=2×2×(﹣3),
∴m=±4,
故答案为:±4.
12.解:由题意得阴影部分面积为,
a +b ﹣﹣=﹣+=(a ﹣ab+b )=[(a+b) ﹣3ab],
∴当a+b=8,ab=2时,
阴影部分面积为,
(8 ﹣3×2)=×58=29,
故答案为:29.
13.解:AP=a,BP=b,
∴AB=a+b,
S正方形APCD=a2,
S正方形PBEF=b2,
又∵点M是AB的中点,a+b=12,
∴AM=BM===6,
∴S△DAM= AM AD= 6 a=3a,
S△MBE= BM BE= 6 b=3b,
∴S阴影面积=(S正方形APCD+S正方形PBEF)﹣(S△DAM+S△MBE)
=(a2+b2)﹣(3a+3b)
=(a2+b2)﹣3(a+b),
∵a+b=12,
∴(a+b)2=144,
∴a2+b2=(a+b)2﹣2ab=144﹣2×9=126,
∴(a2+b2)﹣3(a+b)
=126﹣3×12
=90.
故答案为:90.
14.解:原式=(a+1)2+a(a+1)2+…+a(a+1)2022
=(a+1)3+…+a(a+1)2022
=(a+1)2023
故答案为:(a+1)2023
15.解:∵(x+y)2=2,(x﹣y)2=8,
∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,
①+②得:2(x2+y2)=10,
∴x2+y2=5.
故答案为:5.
16.解:∵x+y=3,x2+y2=23,
∴2xy=(x+y)2﹣(x2+y2)=32﹣23=﹣14,
∴xy=﹣7;
∴(x﹣y)2=(x+y)2﹣4xy=32﹣4×(﹣7)=37.
故答案为:37.
17.解:∵(a+b+1)(a+b﹣1)=24,
∴[(a+b)+1][(a+b)﹣1]=24,
∴(a+b)2﹣1=24,
∴(a+b)2=25,
∴a+b=±5,
∵(a2+b2+1)(a2+b2﹣1)=24,
∴[(a2+b2)+1][(a2+b2)﹣1]=24,
∴(a2+b2)2﹣1=24,
∴(a2+b2)2=25,
∵a2≥0,b2≥0,
∴a2+b2≥0,
∴a2+b2=5,
故答案为:±5,5.
18.解:设一张长方形纸片的长为x,宽为y,长方形ABCD的长AD为a,宽AB为b,
S=2y(a﹣2x)﹣x(a﹣3y)=a(2y﹣x)+xy,
∵当BC的长度变化时,按照同样的放置方式,S始终不变,
∴2y﹣x=0,
∴x=2y,
∵一张长方形纸片的周长为30,
∴(x+y)×2=30,
∴x+y=15,
∴2y+y=15,
解得y=5,
∴x=10,
∴一张长方形纸片的面积是xy=10×5=50,
故答案为:50.
三.解答题
19.解:原式=x2﹣2x﹣(x2﹣4)
=x2﹣2x﹣x2+4
=﹣2x+4,
当x=时,原式=﹣1+4=3.
20.解:原式=x2﹣(2y﹣3)2
=x2﹣(4y2﹣12y+9)
=x2﹣4y2+12y﹣9.
21.解:原式=
=
=2022.
22.解:(1)∵a+b=5,ab=,
∴(a+b)2=25,
∴a2+2ab+b2=25,
∴a2+b2=25﹣2ab=25﹣=;
(2)∵a2+b2=,ab=,
∴a2+b2﹣2ab=16,
∴(a﹣b)2=16,
∴a﹣b=±4.
23.解:(2a﹣b)2﹣(a﹣2b)(a+2b)+(6a2b+8ab2)÷2b
=4a2﹣4ab+b2﹣a2+4b2+3a2+4ab
=6a2+5b2,
当a=2,b=﹣1时,原式=6a2+5b2
=6×22+5×(﹣1)2
=6×4+5×1
=24+5
=29.
24.解:原式=a2﹣4ab+4b2﹣(b+2a)(b﹣2a)﹣4a2+4ab
=a2﹣4ab+4b2﹣b2+4a2﹣4a2+4ab
=a2+3b2.
25.解:(1)原式=(4x2﹣9y2)2
=16x4﹣72x2y2+81y4;
(2)原式=(x2﹣1)(x2+1)(x4+1)
=(x4﹣1)(x4+1)
=x8﹣1.
26.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
27.解:(1)图②中,S阴影=a2+b2,还可以表示为:S阴影=(a+b)2﹣2ab.
∴a2+b2=(a+b)2﹣2ab.
(2)设a=2022﹣m,b=2019﹣m,
则ab=3505,a﹣b=3.
∴(2022﹣m)2+(2019﹣m)2=a2+b2
=(a﹣b)2+2ab
=9+7010
=7019.
28.解:(1)(a+b)(a﹣b)=a2﹣b2;
故答案为(a+b)(a﹣b)=a2﹣b2,平方差.
(2)①原式=(10+0.3)(10﹣0.3)=102﹣0.32=100﹣0.09=99.91;
②原式=(x﹣3z)2﹣(2y)2=x2﹣6xz+9z2﹣4y2.
29.解:(1)由题意可得,图1中两个阴影图形面积的和为a2+b2或(a+b)2﹣2ab;
故答案应为:(1)a2+b2,a2+2ab+b2;
(2)从(1)中结论可得a2+b2=(a+b)2﹣2ab.
故答案应为:a2+b2=(a+b)2﹣2ab;
(3)①由a2+b2=(a+b)2﹣2ab可得,
2ab=(a+b)2﹣(a2+b2)
∴ab=,
∴当a+b=4,a2+b2=10时,
ab==3.
②由①得ab=,
=
=12,
可得
=
=6.
故答案应为:①3,②6.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
