人教版七年级数学上册 3.4 实际问题与一元一次方程 第1课时 课件(共16张)
文档属性
| 名称 | 人教版七年级数学上册 3.4 实际问题与一元一次方程 第1课时 课件(共16张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 770.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
3.4 实际问题与一元一次方程(1)
生活中,有很多需要进行配套的问题,比如我们使用的餐桌,需要和椅子进行配套,你能举出生活中一些配套的问题吗?
问题情境
例1 某车间有22名工人,每人每天可以生产
1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题探究
产品类型 生产人数 每人每天产量 每天产品数量
螺钉
螺母
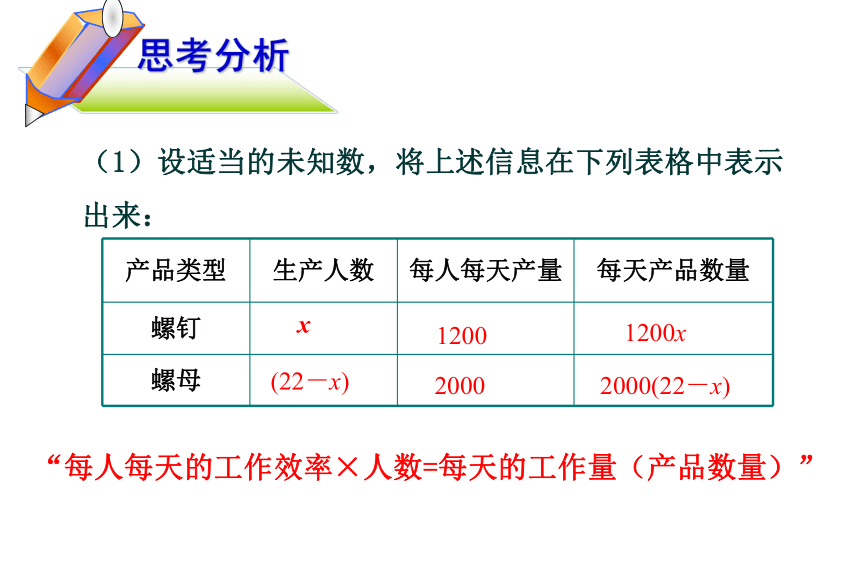
(1)设适当的未知数,将上述信息在下列表格中表示出来:
(22-x)
1200x
2000(22-x)
“每人每天的工作效率×人数=每天的工作量(产品数量)”
思考分析
x
1200
2000
(2)要使每天生产的螺钉和螺母刚好配套,则它们个数之间存在着怎样的数量关系?
“1个螺钉要配2个螺母”
“螺钉和螺母的数量谁多谁少?数量关系如何?”
思考分析
螺钉数量1200x
螺母数量2000(22-x)
解:设应安排 x 名工人生产螺钉,________名工人生产螺母,由题意得
2×1 200 x = 2 000 ( 22 - x).
去括号,得
2 400 x = 44 000 – 2 000 x.
移项,合并同类项,得
4 400 x = 44 000.
x = 10.
生产螺母的人数为
22 – x = 12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
(22–x)
例题探究
例2 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
例题探究
人均效率 人数 时间 工作量
前一部分工作 x
后一部分工作
(1)通过表格对题目数量关系进行分析:
x+2
4
(2)总的工作量与两部分工作量之间有什么关系?
8
总工作量=两部分工作量之和
×
=
×
×
×
=
思考分析
解:设安排 x人先做4 h,根据题意可得
解方程得 x=2.
答:应安排2人先做4 h.
例题解析
(1)用一元一次方程解决实际问题的基本过程:
审(借助表格提炼信息,理解问题中的基本数学关系);
设(用代数式表示实际问题中的文字语言,文字语言符号化);
列(找到所列代数式中的基本等量关系,列出方程);
解(求方程的解);
验(把方程的解代入方程后成立,并符合实际意义);
答(写出实际问题的答案).
归纳反思
实际问题
设安排x名工人
生产 螺钉
解方程
一元一次方程的解(x=a)
检验
实际问题
的答案
规划分工,使两种产品数量上成为配套的问题
设未知数、 列方程
一元一次方程
代入方程成立
符合实际意义
2 000(22 - x)=2 ×1200 x
x=10
22 - x =12
解一元一次方程
应该安排10名工人生产螺钉,12名工人生产螺母
(2)用一元一次方程解决实际问题的基本模型
1.一套仪器由一个A部件和三个B部件构成. 用1 m3钢材可以做40个A部件或240个B部件. 现要用6 m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用 x m3钢材做A部件,(6-x) m3 钢材做B部件. 依题意得:
3×40 x=240 (6-x)
解方程,得:x=4.
答:应用4 m3钢材做A部件,2 m3 钢材做B部件,配成这种仪器160套.
巩固练习
解:设需要 x 天铺好,依题意,得:
解得: x = 8
答:需要8天铺好。
2.一条地下管线由甲工程队单独铺设需要12天、乙工程队单独铺设需要24天.如果两队从两端同时相向施工,需要多少天铺好?
巩固练习
思考一下
本节课学习了哪些主要内容?
你有哪些收获?
课堂小结
必须做一做:课本106页 3、4、5题;
努力试一试:自己设计一道配套问题或工程问题,并解决。
课下作业
3.4 实际问题与一元一次方程(1)
生活中,有很多需要进行配套的问题,比如我们使用的餐桌,需要和椅子进行配套,你能举出生活中一些配套的问题吗?
问题情境
例1 某车间有22名工人,每人每天可以生产
1200个螺钉或2000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
例题探究
产品类型 生产人数 每人每天产量 每天产品数量
螺钉
螺母
(1)设适当的未知数,将上述信息在下列表格中表示出来:
(22-x)
1200x
2000(22-x)
“每人每天的工作效率×人数=每天的工作量(产品数量)”
思考分析
x
1200
2000
(2)要使每天生产的螺钉和螺母刚好配套,则它们个数之间存在着怎样的数量关系?
“1个螺钉要配2个螺母”
“螺钉和螺母的数量谁多谁少?数量关系如何?”
思考分析
螺钉数量1200x
螺母数量2000(22-x)
解:设应安排 x 名工人生产螺钉,________名工人生产螺母,由题意得
2×1 200 x = 2 000 ( 22 - x).
去括号,得
2 400 x = 44 000 – 2 000 x.
移项,合并同类项,得
4 400 x = 44 000.
x = 10.
生产螺母的人数为
22 – x = 12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
(22–x)
例题探究
例2 整理一批图书,由一个人做要40 h完成.现在计划由一部分人先做4 h,再增加2人和他们一起做8 h,完成这项工作.假设这些人的工作效率相同,具体应先安排多少人工作?
例题探究
人均效率 人数 时间 工作量
前一部分工作 x
后一部分工作
(1)通过表格对题目数量关系进行分析:
x+2
4
(2)总的工作量与两部分工作量之间有什么关系?
8
总工作量=两部分工作量之和
×
=
×
×
×
=
思考分析
解:设安排 x人先做4 h,根据题意可得
解方程得 x=2.
答:应安排2人先做4 h.
例题解析
(1)用一元一次方程解决实际问题的基本过程:
审(借助表格提炼信息,理解问题中的基本数学关系);
设(用代数式表示实际问题中的文字语言,文字语言符号化);
列(找到所列代数式中的基本等量关系,列出方程);
解(求方程的解);
验(把方程的解代入方程后成立,并符合实际意义);
答(写出实际问题的答案).
归纳反思
实际问题
设安排x名工人
生产 螺钉
解方程
一元一次方程的解(x=a)
检验
实际问题
的答案
规划分工,使两种产品数量上成为配套的问题
设未知数、 列方程
一元一次方程
代入方程成立
符合实际意义
2 000(22 - x)=2 ×1200 x
x=10
22 - x =12
解一元一次方程
应该安排10名工人生产螺钉,12名工人生产螺母
(2)用一元一次方程解决实际问题的基本模型
1.一套仪器由一个A部件和三个B部件构成. 用1 m3钢材可以做40个A部件或240个B部件. 现要用6 m3钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
解:设应用 x m3钢材做A部件,(6-x) m3 钢材做B部件. 依题意得:
3×40 x=240 (6-x)
解方程,得:x=4.
答:应用4 m3钢材做A部件,2 m3 钢材做B部件,配成这种仪器160套.
巩固练习
解:设需要 x 天铺好,依题意,得:
解得: x = 8
答:需要8天铺好。
2.一条地下管线由甲工程队单独铺设需要12天、乙工程队单独铺设需要24天.如果两队从两端同时相向施工,需要多少天铺好?
巩固练习
思考一下
本节课学习了哪些主要内容?
你有哪些收获?
课堂小结
必须做一做:课本106页 3、4、5题;
努力试一试:自己设计一道配套问题或工程问题,并解决。
课下作业
