第十章 三角形的有关证明章末复习试题(含答案)
文档属性
| 名称 | 第十章 三角形的有关证明章末复习试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-29 15:01:45 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《第十章 三角形的有关证明》
章末复习
考点突破
考点一 全等三角形
1.如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
2.如图,在△ABC中,AB=AC,D是直线BC上一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠BAC=∠DAE=58°,连接CE,则∠BCE的度数为_______.
3.如图,点C,E,F,B在同一条直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
考点二 等腰三角形与等边三角形
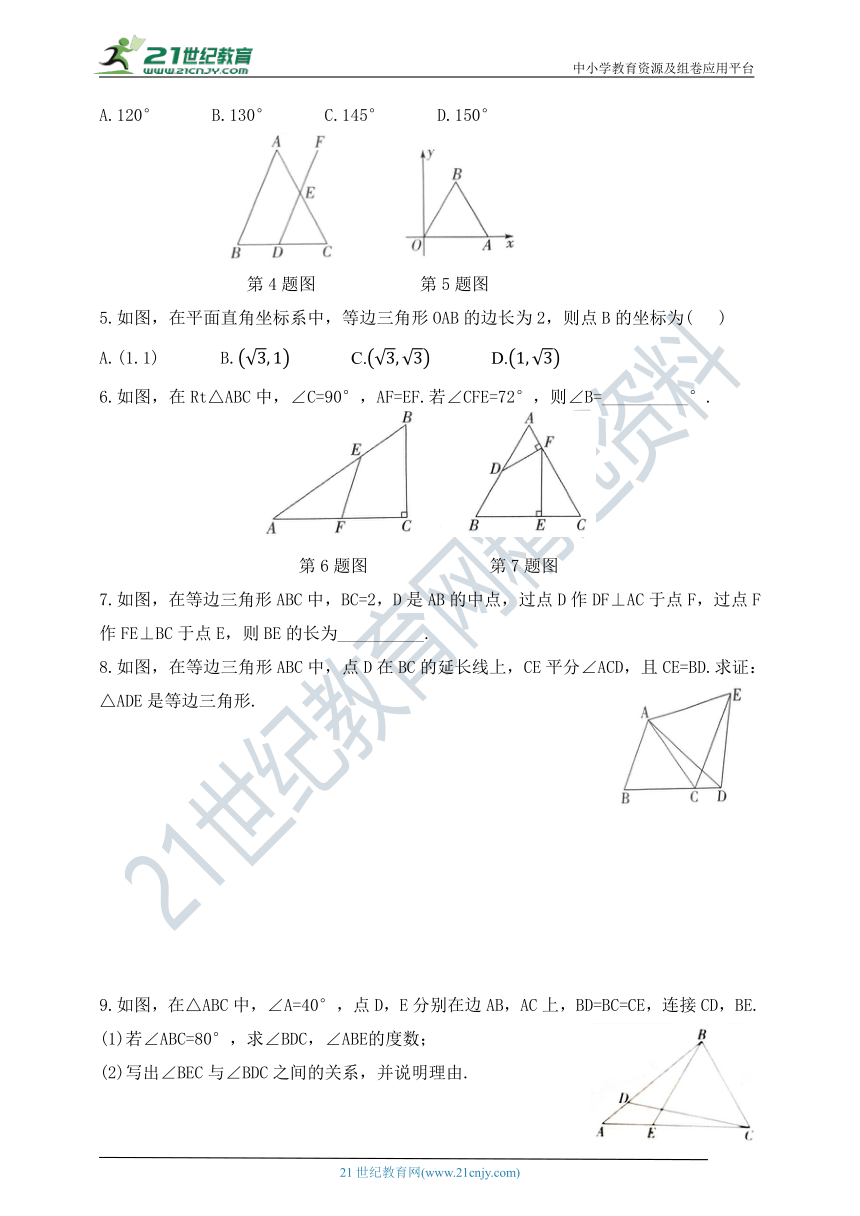
4.如图,在△ABC中,AB=AC,∠C=65°,D是边BC上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
第4题图 第5题图
5.如图,在平面直角坐标系中,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1.1) B. C. D.
6.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B=__________°.
第6题图 第7题图
7.如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则BE的长为__________.
8.如图,在等边三角形ABC中,点D在BC的延长线上,CE平分∠ACD,且CE=BD.求证:△ADE是等边三角形.
9.如图,在△ABC中,∠A=40°,点D,E分别在边AB,AC上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的关系,并说明理由.
考点三 直角三角形
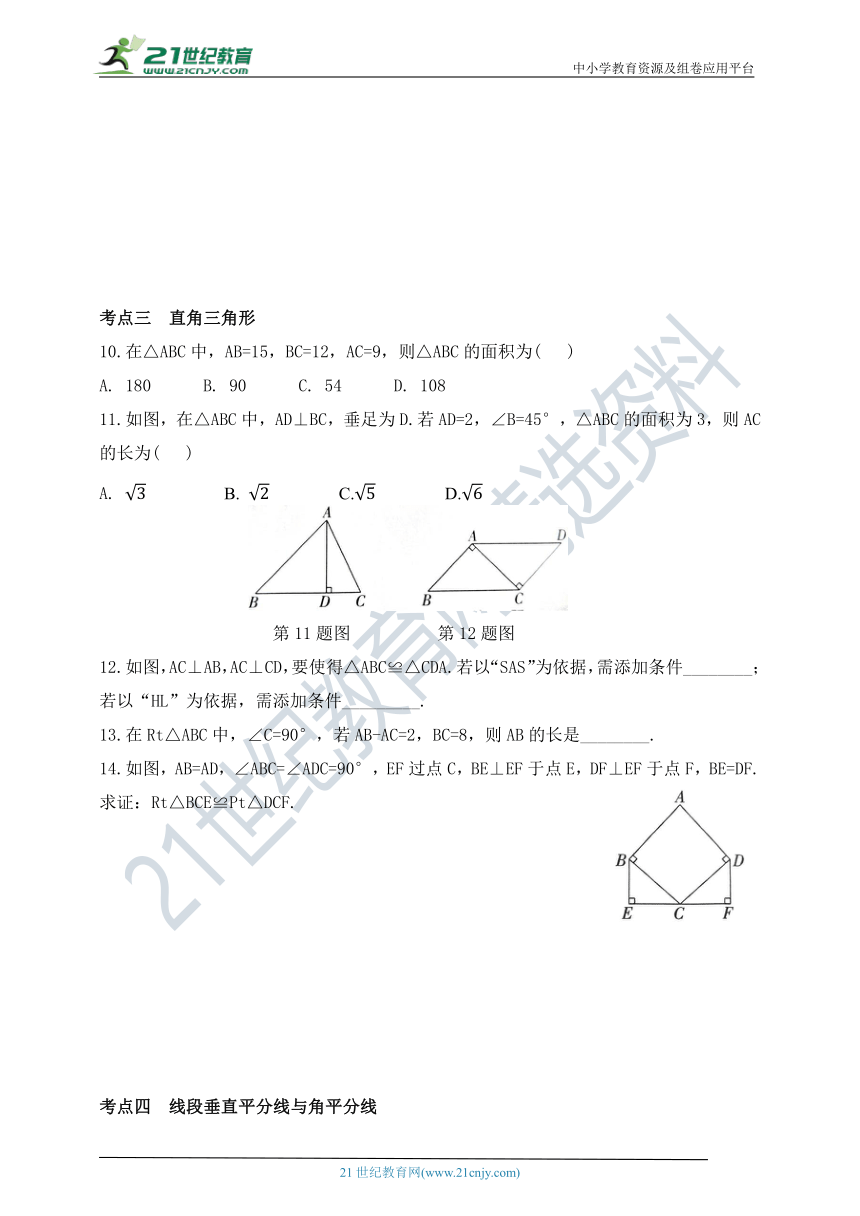
10.在△ABC中,AB=15,BC=12,AC=9,则△ABC的面积为( )
A. 180 B. 90 C. 54 D. 108
11.如图,在△ABC中,AD⊥BC,垂足为D.若AD=2,∠B=45°,△ABC的面积为3,则AC的长为( )
A. B. C. D.
第11题图 第12题图
12.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.若以“SAS”为依据,需添加条件________;若以“HL”为依据,需添加条件_________.
13.在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是________.
14.如图,AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于点E,DF⊥EF于点F,BE=DF.求证:Rt△BCE≌Pt△DCF.
考点四 线段垂直平分线与角平分线
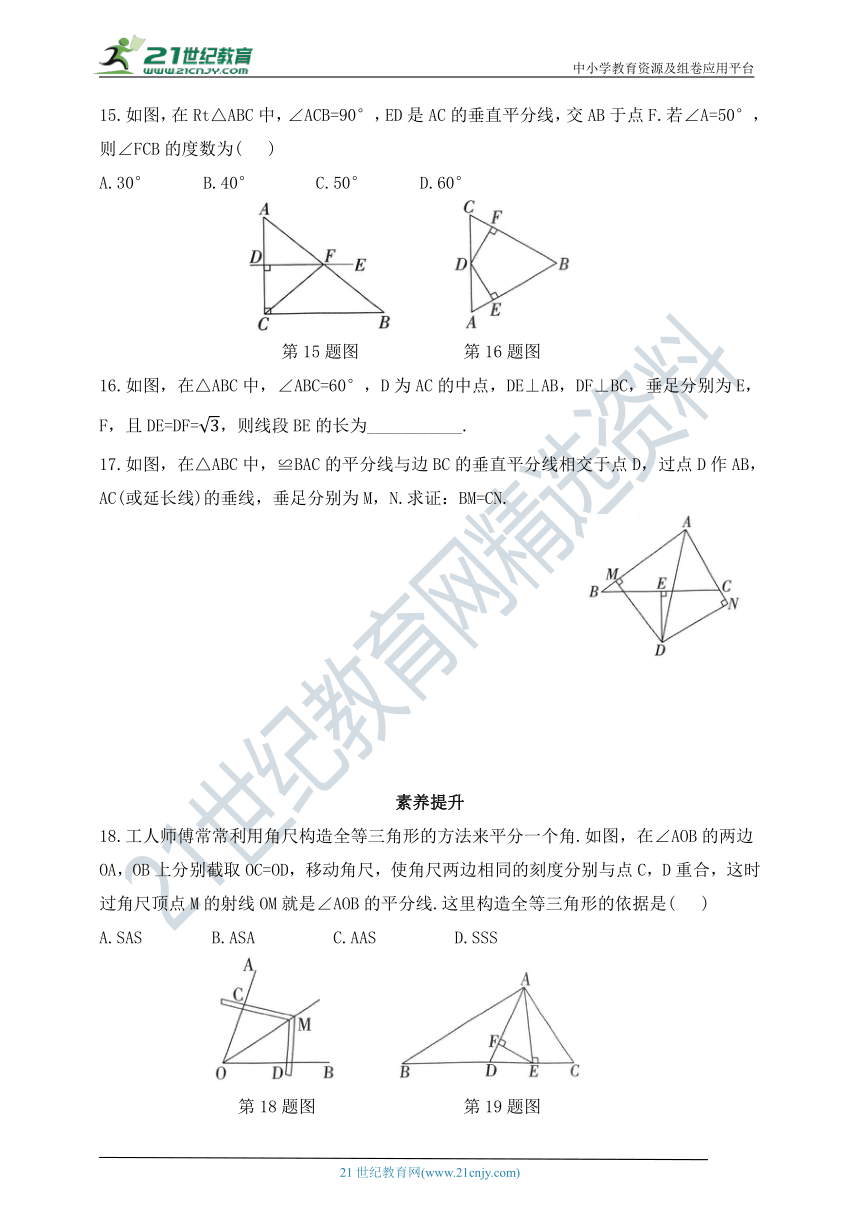
15.如图,在Rt△ABC中,∠ACB=90°,ED是AC的垂直平分线,交AB于点F.若∠A=50°,则∠FCB的度数为( )
A.30° B.40° C.50° D.60°
第15题图 第16题图
16.如图,在△ABC中,∠ABC=60°,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为E,F,且DE=DF=,则线段BE的长为___________.
17.如图,在△ABC中,≌BAC的平分线与边BC的垂直平分线相交于点D,过点D作AB,AC(或延长线)的垂线,垂足分别为M,N.求证:BM=CN.
素养提升
18.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA,OB上分别截取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是( )
A.SAS B.ASA C.AAS D.SSS
第18题图 第19题图
19.如图,在△ABC中,∠B=30°,∠C=60°,AE⊥BC于点E,AD平分∠BAE,EF⊥AD于点F.有下列结论:①∠DEF=30°;②AD=AC;③△AFE≌△AEC;④DE=CE,其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
20.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个小正方形和两对全等的直角三角形(如图).若AF=5,CE=12,则该三角形的面积为( )
A. 60 B. 65 C. 120 D. 130
第20题图 第21题图
21.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.给出下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中,正确的个数为( )
A.1 B.2 C.3 D.4
22.如图,AB=AC,DB=DC.若∠ABC为60°,BE=3cm,则AB=_________ cm.
第22题图 第23题图
23.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=____________ cm.
24.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,E为边AD上一点,连接BD,CE交于点F,且CE∥AB.若AB=4,CE=3,则BC的长为_________.
25.如图,CD平分∠ACB,D是AB的中点,AE∥DC,AE交BC的延长线于点E,且∠ACE=60°,BC=8.求△ACE的周长.
26.在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择一个.补充在下面的问题中并解答.
问题:如图,在△ABC中,∠ABC=∠ACB,点D在边AB上(不与点A,B重合),点E在边AC上(不与点A,C重合),连接BE,CD,BE与CD相交于点F.若__________________,求证:BE=CD.
27.如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,P是BA的延长线上一点,O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
28.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动的时间为t S.
(1)求BC的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
29.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,点E在AB上,且AE=AC,连接DE.
(1)求证:△ADE≌△ADC;
(2)若E为AB的中点,求∠B的度数;
(3)若AC=6,BC=8,求BD的长.
参考答案
[考点突破]
1.D 2.122°
3.(1)∵AB∥CD,∴∴∠B=∠C.在△ABE和△DCF中,∴△ABE≌△DCF.∴AB=CD
(2)由(1)得△ABE≌△DCF,∴AB=CD,BE=CF,∠B=∠C.∵∠B=40°,∴∠C=40°.∵AB=CF,∴CF=CD.∴∠D=∠CFD=.
4. B 5. D 6. 54 7.
8.∵△ABC为等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=AC.∴∠ACD=120°.∵CE平分∠ACD,∴∠ACE=60°=∠B.在△ABD和△ACE中,∴△ABD≌△ACE.∴AD=AE,∠BAD=∠CAE.∴∠BAD-∠CAD=∠CAE-∠CAD,即∠BAC=∠DAE.又∵∠BAC=60°,∴∠DAE=60°.又∵AD=AE,∴△ADE为等边三角形.
9.(1)∵∠ABC=80°,BD=BC,∴∠BDC=∠BCD= ×(180°-80°)=50°,∵∠A+∠ABC+∠ACB=180°,∠ A=40°,∴∠ACB=180°-40°-80°=60°.∵CE=BC,∴BCE是等边三角形.∴∠EBC=60°.∴∠ABE=∠ABC-∠EBC=20°.
(2)∠BEC+∠BDC=110° 理由:设∠BEC=α,∠BDC=β.在△ABE中,a=∠A+∠ABE=40°+∠ABE.∵CE=BC,∴∠CBE=∠BEC=a.∴∠ABC=∠ABE+∠CBE=∠A+2∠ABE=40°+2∠ABE.∵在△BDC中,BD=BC,∴∠BDC+∠BCD+∠DBC=2β+40°+2∠ABE=180°.∴β=70°-∠ABE.∴α+β=40°+∠ABE+70°-∠ABE=110°,即∠BEC+∠BDC=110°.
10.C 11.C 12.AB=CD BC=DA 13.17
14.连接BD.∵AB=AD,∴∠ABD=∠ADB.∵∠ABC=∠ADC=90°,∴∠CBD=∠CDB.∴BC=DC.∵BE⊥EF,DF⊥EF,∴∠E=∠F=90°.在Rt△BCE和Rt△DCF中,∴Rt△BCE≌Rt△DCF
15.B 16.3
17.连接BD,CD.∶∵DE是BC的垂直平分线,∴BD=CD. AD是∠BAC的平分线,DM⊥AB,DN⊥AC,∴DM=DN.在Rt△BMD和Rt△CND中,∴Rt△BMD≌Rt△CND.∴BM=CN .
[素养提升]
18.D 19.C 20.A 21.C 22.6 23.6 24.
25.如图,过点D作DM⊥AC于点M,DF⊥BC于点F. CCD平分∠ACB,∴DM=DF,∵D是AB的中点,∴DB=DA,在Rt△DBF和Rt△DAM中,∴Rt△DBF≌Rt△DAM..∴∠DBF=∠DAM.∴CA=CB=8.又∵∠ACE=60°,∴∠ACB=120°.又∵CD平分∠ACB,∴∠BCD=60°.∵AE∥DC,∴∠AEC=∠BCD=60°.∴△ACE是等边三角形.∴△ACE的周长为8×3=24 .
26.答案不唯一,如选①AD=AE ∵∠ABC=∠ACB,∴AB=AC.
在△ABE和△ACD中, ∴△ABE≌△ACD.∴BE=CD
27.(1)连接OB.∵AB=AC,AD⊥BC,∴BD=CD, °=60°.∴OB=OC,∠ABC=90°-∠BAD=30°.∵OP=OC,∴OB=OC=OP.∴∠APO=∠ABO,∠DCO=∠DBO.∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°.
(2)∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°. ∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°.∴∠POC=180°-(∠OPC+∠OCP)=60°.∵OP=OC,∴△OPC是等边三角形.∴OP=PC.∴点P在OC的垂直平分线上.
28.(1)在Rt△ABC中,由勾股定理,得 ∴BC=4cm.
(2)由题意,知BP=t cm.①当∠APB=90°时,点P与点C重合,BP=BC=4cm,即t=4.②当∠BAP=90°时,CP=(t-4) cm.在Rt△ACP中,由勾股定理,得 即 在Rt△BAP中,由勾股定理,得 即52+ 解得 综上所述,当△ABP为直角三角形时,t的值为4或
(3)①当AB=BP时,BP=5 cm,∴t=5.②当AB=AP时,BP=2BC=8cm,∴t=8.③当BP=AP时,AP=BP=tm,CP=|t-4|cm.在Rt△ACP中,由勾股定理,得 即 解得t= ,综上所述,当△ABP为等腰三角形时,t的值为5或8或 .
29.(1)∵AD平分∠CAB,∴∠CAD=∠EAD.在△ADE和△ADC中,
∴△ADE≌△ADC .
(2)∵△ADE≌△ADC,∴∠C=∠AED=90°.∵E为AB的中点,∴AE=BE,∴DE为AB的垂直平分线.∴AD=BD.∴∠B=∠DAE.∴∠CAD=∠DAE=∠B.∵∠CAD+∠DAE+∠B=90°,∴∠B=30°
(3)∵∠ACB=90°,AC=6,BC=8,∴AB=10.∵AC=AE=6,∴BE=4.设BD=x,∵△ADE≌△ADC,∴DE=CD=8-x.∵在Rt△BDE中,由勾股定理.得 BD2,即 解得x=5,即BD=5 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《第十章 三角形的有关证明》
章末复习
考点突破
考点一 全等三角形
1.如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c B.b+c C.a-b+c D.a+b-c
2.如图,在△ABC中,AB=AC,D是直线BC上一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠BAC=∠DAE=58°,连接CE,则∠BCE的度数为_______.
3.如图,点C,E,F,B在同一条直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=40°,求∠D的度数.
考点二 等腰三角形与等边三角形
4.如图,在△ABC中,AB=AC,∠C=65°,D是边BC上任意一点,过点D作DF∥AB交AC于点E,则∠FEC的度数是( )
A.120° B.130° C.145° D.150°
第4题图 第5题图
5.如图,在平面直角坐标系中,等边三角形OAB的边长为2,则点B的坐标为( )
A.(1.1) B. C. D.
6.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B=__________°.
第6题图 第7题图
7.如图,在等边三角形ABC中,BC=2,D是AB的中点,过点D作DF⊥AC于点F,过点F作FE⊥BC于点E,则BE的长为__________.
8.如图,在等边三角形ABC中,点D在BC的延长线上,CE平分∠ACD,且CE=BD.求证:△ADE是等边三角形.
9.如图,在△ABC中,∠A=40°,点D,E分别在边AB,AC上,BD=BC=CE,连接CD,BE.
(1)若∠ABC=80°,求∠BDC,∠ABE的度数;
(2)写出∠BEC与∠BDC之间的关系,并说明理由.
考点三 直角三角形
10.在△ABC中,AB=15,BC=12,AC=9,则△ABC的面积为( )
A. 180 B. 90 C. 54 D. 108
11.如图,在△ABC中,AD⊥BC,垂足为D.若AD=2,∠B=45°,△ABC的面积为3,则AC的长为( )
A. B. C. D.
第11题图 第12题图
12.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.若以“SAS”为依据,需添加条件________;若以“HL”为依据,需添加条件_________.
13.在Rt△ABC中,∠C=90°,若AB-AC=2,BC=8,则AB的长是________.
14.如图,AB=AD,∠ABC=∠ADC=90°,EF过点C,BE⊥EF于点E,DF⊥EF于点F,BE=DF.求证:Rt△BCE≌Pt△DCF.
考点四 线段垂直平分线与角平分线
15.如图,在Rt△ABC中,∠ACB=90°,ED是AC的垂直平分线,交AB于点F.若∠A=50°,则∠FCB的度数为( )
A.30° B.40° C.50° D.60°
第15题图 第16题图
16.如图,在△ABC中,∠ABC=60°,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为E,F,且DE=DF=,则线段BE的长为___________.
17.如图,在△ABC中,≌BAC的平分线与边BC的垂直平分线相交于点D,过点D作AB,AC(或延长线)的垂线,垂足分别为M,N.求证:BM=CN.
素养提升
18.工人师傅常常利用角尺构造全等三角形的方法来平分一个角.如图,在∠AOB的两边OA,OB上分别截取OC=OD,移动角尺,使角尺两边相同的刻度分别与点C,D重合,这时过角尺顶点M的射线OM就是∠AOB的平分线.这里构造全等三角形的依据是( )
A.SAS B.ASA C.AAS D.SSS
第18题图 第19题图
19.如图,在△ABC中,∠B=30°,∠C=60°,AE⊥BC于点E,AD平分∠BAE,EF⊥AD于点F.有下列结论:①∠DEF=30°;②AD=AC;③△AFE≌△AEC;④DE=CE,其中,正确的有( )
A.1个 B.2个 C.3个 D.4个
20.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个小正方形和两对全等的直角三角形(如图).若AF=5,CE=12,则该三角形的面积为( )
A. 60 B. 65 C. 120 D. 130
第20题图 第21题图
21.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.给出下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中,正确的个数为( )
A.1 B.2 C.3 D.4
22.如图,AB=AC,DB=DC.若∠ABC为60°,BE=3cm,则AB=_________ cm.
第22题图 第23题图
23.如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=____________ cm.
24.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,E为边AD上一点,连接BD,CE交于点F,且CE∥AB.若AB=4,CE=3,则BC的长为_________.
25.如图,CD平分∠ACB,D是AB的中点,AE∥DC,AE交BC的延长线于点E,且∠ACE=60°,BC=8.求△ACE的周长.
26.在①AD=AE,②∠ABE=∠ACD,③FB=FC这三个条件中选择一个.补充在下面的问题中并解答.
问题:如图,在△ABC中,∠ABC=∠ACB,点D在边AB上(不与点A,B重合),点E在边AC上(不与点A,C重合),连接BE,CD,BE与CD相交于点F.若__________________,求证:BE=CD.
27.如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,P是BA的延长线上一点,O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
28.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1 cm/s的速度运动,设运动的时间为t S.
(1)求BC的长;
(2)当△ABP为直角三角形时,求t的值;
(3)当△ABP为等腰三角形时,求t的值.
29.如图,在Rt△ABC中,∠ACB=90°,AD平分∠CAB交BC于点D,点E在AB上,且AE=AC,连接DE.
(1)求证:△ADE≌△ADC;
(2)若E为AB的中点,求∠B的度数;
(3)若AC=6,BC=8,求BD的长.
参考答案
[考点突破]
1.D 2.122°
3.(1)∵AB∥CD,∴∴∠B=∠C.在△ABE和△DCF中,∴△ABE≌△DCF.∴AB=CD
(2)由(1)得△ABE≌△DCF,∴AB=CD,BE=CF,∠B=∠C.∵∠B=40°,∴∠C=40°.∵AB=CF,∴CF=CD.∴∠D=∠CFD=.
4. B 5. D 6. 54 7.
8.∵△ABC为等边三角形,∴∠B=∠ACB=∠BAC=60°,AB=AC.∴∠ACD=120°.∵CE平分∠ACD,∴∠ACE=60°=∠B.在△ABD和△ACE中,∴△ABD≌△ACE.∴AD=AE,∠BAD=∠CAE.∴∠BAD-∠CAD=∠CAE-∠CAD,即∠BAC=∠DAE.又∵∠BAC=60°,∴∠DAE=60°.又∵AD=AE,∴△ADE为等边三角形.
9.(1)∵∠ABC=80°,BD=BC,∴∠BDC=∠BCD= ×(180°-80°)=50°,∵∠A+∠ABC+∠ACB=180°,∠ A=40°,∴∠ACB=180°-40°-80°=60°.∵CE=BC,∴BCE是等边三角形.∴∠EBC=60°.∴∠ABE=∠ABC-∠EBC=20°.
(2)∠BEC+∠BDC=110° 理由:设∠BEC=α,∠BDC=β.在△ABE中,a=∠A+∠ABE=40°+∠ABE.∵CE=BC,∴∠CBE=∠BEC=a.∴∠ABC=∠ABE+∠CBE=∠A+2∠ABE=40°+2∠ABE.∵在△BDC中,BD=BC,∴∠BDC+∠BCD+∠DBC=2β+40°+2∠ABE=180°.∴β=70°-∠ABE.∴α+β=40°+∠ABE+70°-∠ABE=110°,即∠BEC+∠BDC=110°.
10.C 11.C 12.AB=CD BC=DA 13.17
14.连接BD.∵AB=AD,∴∠ABD=∠ADB.∵∠ABC=∠ADC=90°,∴∠CBD=∠CDB.∴BC=DC.∵BE⊥EF,DF⊥EF,∴∠E=∠F=90°.在Rt△BCE和Rt△DCF中,∴Rt△BCE≌Rt△DCF
15.B 16.3
17.连接BD,CD.∶∵DE是BC的垂直平分线,∴BD=CD. AD是∠BAC的平分线,DM⊥AB,DN⊥AC,∴DM=DN.在Rt△BMD和Rt△CND中,∴Rt△BMD≌Rt△CND.∴BM=CN .
[素养提升]
18.D 19.C 20.A 21.C 22.6 23.6 24.
25.如图,过点D作DM⊥AC于点M,DF⊥BC于点F. CCD平分∠ACB,∴DM=DF,∵D是AB的中点,∴DB=DA,在Rt△DBF和Rt△DAM中,∴Rt△DBF≌Rt△DAM..∴∠DBF=∠DAM.∴CA=CB=8.又∵∠ACE=60°,∴∠ACB=120°.又∵CD平分∠ACB,∴∠BCD=60°.∵AE∥DC,∴∠AEC=∠BCD=60°.∴△ACE是等边三角形.∴△ACE的周长为8×3=24 .
26.答案不唯一,如选①AD=AE ∵∠ABC=∠ACB,∴AB=AC.
在△ABE和△ACD中, ∴△ABE≌△ACD.∴BE=CD
27.(1)连接OB.∵AB=AC,AD⊥BC,∴BD=CD, °=60°.∴OB=OC,∠ABC=90°-∠BAD=30°.∵OP=OC,∴OB=OC=OP.∴∠APO=∠ABO,∠DCO=∠DBO.∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°.
(2)∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°. ∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°.∴∠POC=180°-(∠OPC+∠OCP)=60°.∵OP=OC,∴△OPC是等边三角形.∴OP=PC.∴点P在OC的垂直平分线上.
28.(1)在Rt△ABC中,由勾股定理,得 ∴BC=4cm.
(2)由题意,知BP=t cm.①当∠APB=90°时,点P与点C重合,BP=BC=4cm,即t=4.②当∠BAP=90°时,CP=(t-4) cm.在Rt△ACP中,由勾股定理,得 即 在Rt△BAP中,由勾股定理,得 即52+ 解得 综上所述,当△ABP为直角三角形时,t的值为4或
(3)①当AB=BP时,BP=5 cm,∴t=5.②当AB=AP时,BP=2BC=8cm,∴t=8.③当BP=AP时,AP=BP=tm,CP=|t-4|cm.在Rt△ACP中,由勾股定理,得 即 解得t= ,综上所述,当△ABP为等腰三角形时,t的值为5或8或 .
29.(1)∵AD平分∠CAB,∴∠CAD=∠EAD.在△ADE和△ADC中,
∴△ADE≌△ADC .
(2)∵△ADE≌△ADC,∴∠C=∠AED=90°.∵E为AB的中点,∴AE=BE,∴DE为AB的垂直平分线.∴AD=BD.∴∠B=∠DAE.∴∠CAD=∠DAE=∠B.∵∠CAD+∠DAE+∠B=90°,∴∠B=30°
(3)∵∠ACB=90°,AC=6,BC=8,∴AB=10.∵AC=AE=6,∴BE=4.设BD=x,∵△ADE≌△ADC,∴DE=CD=8-x.∵在Rt△BDE中,由勾股定理.得 BD2,即 解得x=5,即BD=5 .
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
