广东省惠州市实验中学2012-2013学年高二上学期期中考试数学(理)试题
文档属性
| 名称 | 广东省惠州市实验中学2012-2013学年高二上学期期中考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 272.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-17 13:10:54 | ||
图片预览



文档简介
考试用时120分钟 满分为150分。
一、选择题:(本大题共8小题,每小题5分,满分40分.)
1.“”是“”成立的 ( )
A. 必要不充分条件. B. 充分条件
C. 充分不必要条件. D. 既不充分也不必要条件.
2.一组数据中的每一个数都减去90得到一组新的数据,如果求得新数据的平均数为1.2,方差为4.4,则原来数据的平均数和方差分别为( )
A.91.2,4.4 B.91.2,94.4 C. 88.8,4.4 D.88.8,75.6
3.四位二进制数能表示的最大十进制数是( )
A.8 B.15 C.31 D.64
4.某产品的广告费用x与销售额y的统计数据如下表
广告费用x(万元)
4
2
3
5
销售额y(万元)
49
26
39
54
根据上表可得回归方程中的为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元 B.65.5万元
C.67.7万元 D.72.0万元
5.定义某种运算,运算原理如图所示,则式子:
的值是( )
A.2 B.6 C. 8 D.7
6. 从1,2,3,4,5中任取两个不同的数字构成一个两位数,这个两位数大于40的概率为 ( )
A. B. C. D.
7.已知椭圆上的点到焦点的距离为2,为的中点,则(为坐标原点)的值为 ( )
A.4 B.2 C.8 D.
8. 如图3,平面中两条直线和相交于点,对于平面上任意一点,
若、分别是到直线和的距离,则称有序非负实数对
是点的“距离坐标”.已知常数,,给出下列命题:
①若,则“距离坐标”为的点有且仅有个;
②若,则“距离坐标”为的点有且仅有个;
③若,则“距离坐标”为的点有且仅有个.
上述命题中,正确命题的个数是 ( )
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,满分30分.)
9. 过点(1,2)且在两坐标轴上的截距相等的直线的方程 ______。
10.若椭圆经过点(2,3),且焦点为,则这个椭圆的标准方程为 .
11.已知函数,(、且是常数).若是从、、、四个数中任取的一个数,是从、、三个数中任取的一个数,则函数为奇函数的概率是____________.
12.右图是底面半径为1,母线长均为2的圆锥和圆柱的组合体,
则该组合体的侧视图的面积为____________________.
13. 直线x+2y=0被曲线x2+y2-6x-2y-15=0所截得的弦长等于____________.
14. 椭圆的焦点F1 、F2,P为椭圆上的一点,已知,则的面积为________
三、解答题(共80分)
15. (本题满分12分)已知函数f(x)=2sin,x∈R.
(1)求f 的值;
(2)设∈,=,f(3β+2π)=,求cos(+β)的值.
16.(本题满分12分)为了对某课题进行研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
(I)求x,y;
(II)若从高校B、C抽取的人中选2人作专题发言,求这2人都来自高校C的概率.
17.(本小题满分14分)已知:p:方程x2-mx+1=0有两个不等的正根;q:不等式|x-1|>m的解集为R。若p或q为真命题,p且q为假命题,求实数m的取值范围。
18. (本小题14分)已知椭圆的离心率为,以原点为圆心,椭圆短半轴长为半径的圆与直线相切,分别是椭圆的左右两个顶点,为椭圆上的动点.
(1)求椭圆的标准方程;
(2)若与均不重合,设直线的斜率分别为,求的值。
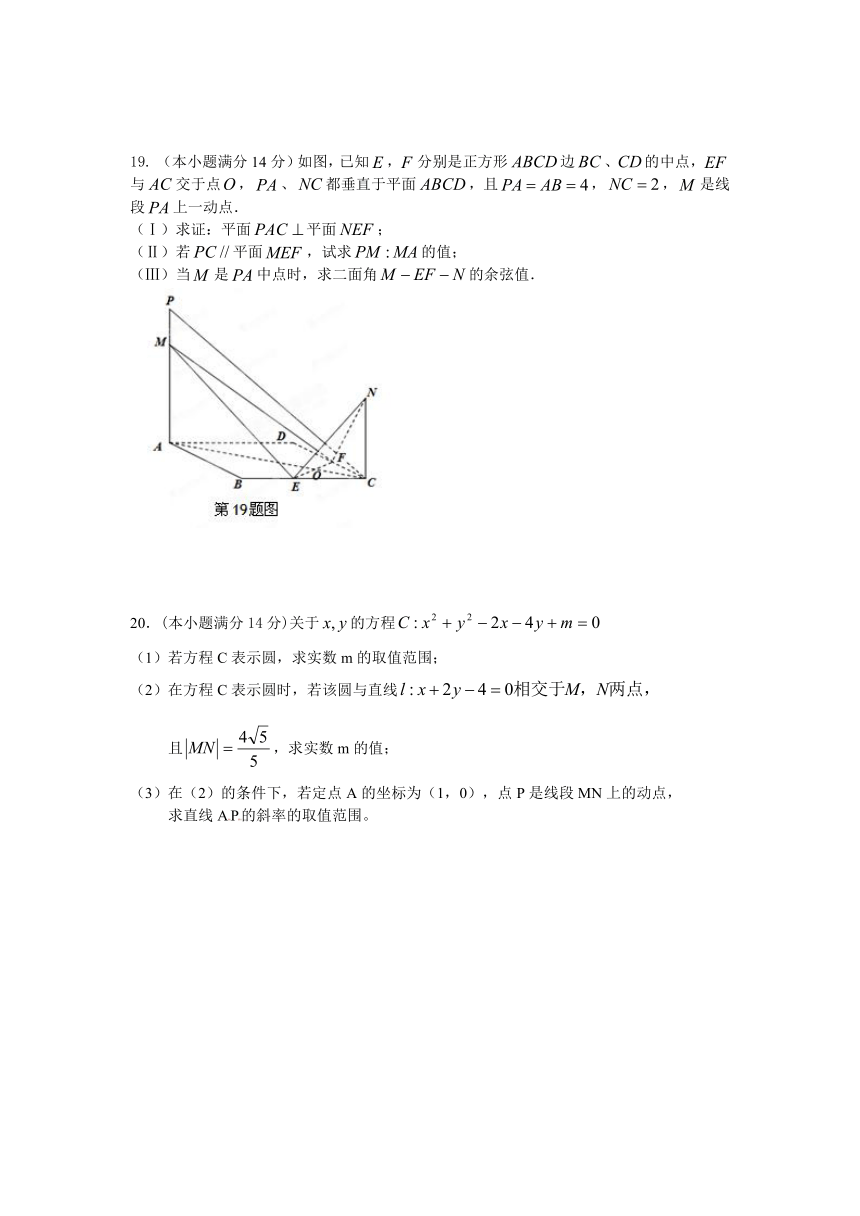
19. (本小题满分14分)如图,已知,分别是正方形边、的中点,与交于点,、都垂直于平面,且,,是线段上一动点.
(Ⅰ)求证:平面平面;
(Ⅱ)若平面,试求的值;
(Ⅲ)当是中点时,求二面角的余弦值.
20.(本小题满分14分)关于的方程
(1)若方程C表示圆,求实数m的取值范围;
(2)在方程C表示圆时,若该圆与直线
且,求实数m的值;
(3)在(2)的条件下,若定点A的坐标为(1,0),点P是线段MN上的动点,
求直线AP的斜率的取值范围。
2012-2013学年度第一学期高二级理科数学期中试题答案
一、选择题(本大题共8小题,每小题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
C
A
B
B
C
B
D
D
二、填空题:(5分×6=30分)
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
16.(本题满分12分)
解:(I)由题意可得 ,所以x=1,y=3
(II)记从高校B抽取的2人为b1,b2, 从高校C抽取的3人为c1,c2,c3,则从高校B、C抽取的5人中选2人作专题发言的基本事件有:
(b1,b2),(b1,c1), (b1,c2), (b1,c3), (b2,c1), (b2,c2), (b2,c3),( c1,c2), ( c1,c3), ( c2,c3)共10种.
设选中的2人都来自高校C的事件为X,则X包含的基本事件有( c1,c2), ( c1,c3), ( c2,c3)共3种.
因此 . 故选中的2人都来自高校C的概率为
18.解:(1)由题意可得圆的方程为直线与圆相切,即又
即得
所以椭圆方程为
(2)设则
即
则
即
的值为
20.解:(Ⅰ)连结,∵平面,平面,∴,
又∵,,∴平面,
又∵,分别是、的中点,∴,
∴平面,又平面,
∴平面平面;---------------------------------------4分
(Ⅱ)连结,∵平面,平面平面,∴,
∴,故 ---------------------8分
(Ⅲ)∵平面,平面,∴ ,
在等腰三角形中,点为的中点,∴,
∴为所求二面角的平面角, --------------10分
∵点是的中点,∴,
所以在矩形中,可求得,,, --12分
在中,由余弦定理可求得,
∴二面角的余弦值为. --------------14分
20.解:(1)方程C可化为:要使该方程表示圆,只需5-m>0.即m<5
所以方程C表示圆时,实数m的取值范围是。
(2)由(1)知,当方程C表示圆时,圆心为C(1,2),半径为。
过圆心C作直线L的垂线CD,D为垂足。 则
又由
同课章节目录
