沪科版数学七年级下8.3完全平方公式与平方差公式(第3课时)(共25张PPT)
文档属性
| 名称 | 沪科版数学七年级下8.3完全平方公式与平方差公式(第3课时)(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 09:26:54 | ||
图片预览





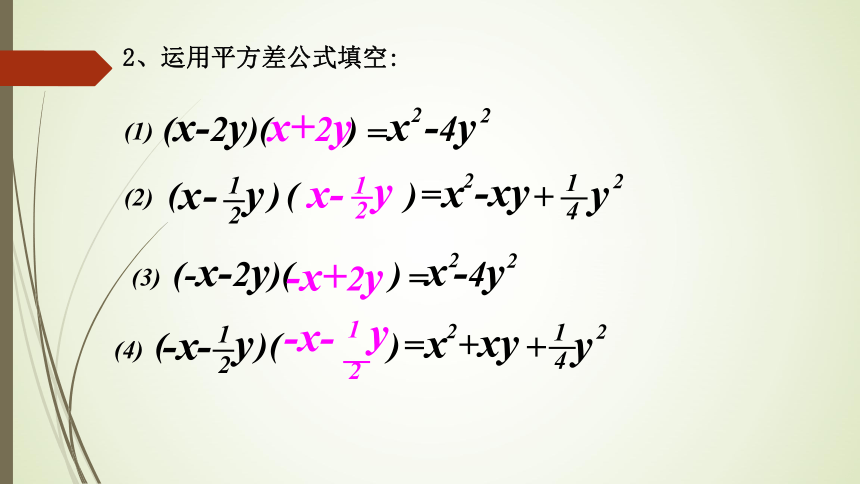



文档简介
(共25张PPT)
第3课时 乘法公式综合练习
8.3 完全平方公式与平方差公式
沪科版数学七年级下
乘法公式
平方差公式
完全平方公式
(a+b)(a-b) =
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x +(a+b)x+ab
2
知识回顾
公式中的a、b即可以是数,也可以是含字母的代数式
比较平方差公式和完全平方公式:
(a-b)(a+b)= a2-b2
( a+ b)2=a2+2 a b+ b2
( a- b)2=a2-2 a b+ b2
公式 相乘多项式的特征 展开式项数
平方差公式 一项相同,另一项相反 2项
完全平方公式 两项都相同 3项
一、乘法公式基础练习
1、运用平方差公式进行计算:
(1)(-5x-3y)(-5x+3y)
解:
(1)(-5x-3y)(-5x+3y)
=(-5x) - (3y)
=25x -9y
解:
解:
应用平方差公式,结果是:
同号项 -异号项
(x-2y)( )
=
x
2
-4y
2
(1)
( )
-x
2
1
y
-
( )
=
x
2
+xy
+
4
1
y
2
(4)
x
-4y
(-x-2y)( )
=
2
2
(3)
( )
x
2
1
y
-
( )
=
x
2
-xy
+
4
1
y
2
(2)
x+2y
-x+2y
x-
2
1
y
-x-
2
1
y
2、运用平方差公式填空:
3、运用完全平方公式进行计算:
(2)原式=(5x+4) -(2x-3)
=25x +40x+16-(4x -12x+9)
=21x +52x+7
公式变形为
(首±尾)2=首2±2×首×尾+尾2
(1)(1-2x)(2x-1)
(3) (1-2x-3y)2
解:
解:
解:
(1)原式=-(2x-1)(2x-1)
=-(2x-1)
=-(4x -4x+1)
=-4x +4x-1
(3)原式=[(1-2x)-3y) ]2
=(1-2x) +2(1-2x)3y+(3y)
=1-4x+4x +6y-12xy+9y
(2)(-5x-4) -(2x-3)
4.下列各式是完全平方式的有( )
②
③ ④
A
①②③ B.②③④
C. ①②④ D.②④
D
1
+
-4
5、若|x+y-5|+(xy-6)2=0,则x2+y2的值为( )
A.13 B.26 C.28 D.37
A
例2.利用乘法公式简便计算:
103×97 (2)101 -99
(3)20222-2019×2025
解:
(1)原式=(100+3)×(100-3)=10000-9=9991
(2)原式=(100+1) -(100-1)
=10000+200+1-10000+200+1
=400
(3)原式=20222-(2022-3)×(2022+3)
= 20222- 20222+9
=9
=(10000-1)
=108-1=99999999
二、乘法公式提升 练习
(2)(-5x-4)(2x+3)(-5x+4)(2x-3)
(3)(-2x -5) -(-2x-5) (2x-5)
1、化简计算
解:
(2)原式=(-5x-4) (-5x+4)(2x+3)(2x-3)
=(25x -16)(4x -9)
=100x4-289x2+144
(3)原式=(4x4+20x+25)-[(-2x-5)(2x-5)]
= 4x4+20x+25-[2x -25]
=4x4+20x+25-(4x4-100x+625)
=120x-600
2、运用乘法公式计算
(1)、(a-2b+3)(a+2b-3)
(3)、( m 2n + 3 )2
(4)、 [(a+b)2+(a-b)2] (a2-b2)
(2)、 (3x2-4x+5)(3x2+4x-5)
=[a-(2b-3)][a+(2b-3)]
=a -2a(2b-3)+(2b-3)
= a -4ab+6a+4b -6b+9
(1)(a-2b+3)(a+2b-3)
解:
(2)、 (3x2-4x+5)(3x2+4x-5)
=[3x -(4x-5)][3x +(4x-5)]
=9x4-6x (4x-5)+(4x-5)
=9x4-24x3+30x +16x -40x+25
=9x4-24x3+46x -40x+25
(3)、( m 2n + 3 )2 =(m-2n) +6(m-2n)+9
=m -4mn+4n +6m-12n+9
(4)、 [(a+b)2+(a-b)2] (a2-b2)
=(2a +2b )] (a2-b2)
=2(a +b )(a2-b2)
=2(a4-b4)=2a4-2b4
(5)、 (x+2y+3z)2-(x-2y+3z)2
(5)、 (x+2y+3z)2-(x-2y+3z)2
=[ (x+3z)2+2×(x+3z)×2y+(2y) ]- [ (x+3z)2-2×(x+3z)×2y+(2y) ]
= 4×(x+3z)×2y
=8xy+24yz
三项组合为两项时,注意括进括号内的项尽量相同,后面化简方便计算
三、乘法公式拓展 练习
a
2
b
2
+
-
ab
+
=
(a+b)
2
(1)
a
2
b
2
+
-ab
+
=
(a-b)
2
(2)
2
(a+b)
-
(a-b)
2
=
(3)
2
(a+b)
+
(a-b)
2
=
(4)
a
2
b
2
+
=
(a+b)
2
+
(a-b)
2
+
=
(5)
3ab
(-ab)
4ab
2a
2
2b
2
+
(-2ab)
2ab
乘法公式变式
填空:
例 1 、已知a+b=5 ,ab= -2,
求(1) a2+b2 (2)a-b
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
例题讲解
解:
(1) a2+b2=(a+b) -2ab
=5 -2×(-2)
=29
(2)∵(a-b) =(a+b)2-4ab
=5 -4×(-2)
=33
∴a-b=±
注意乘法公式变化规律
例2、 已知x+y=4,x2+y2=10,求xy和x-y的值.
解:由x+y=4,可得(x+y)2=16,
即 x2+2xy+y2=16.
∵ x2+y2=10,
∴ xy=3.
∵ (x-y)2=x2+y2-2xy=10-2×3=4,
∴ x-y=±2.
注意:由(x-y)2=4,求x-y,有两解,不能遗漏!
例3、如果a+的值
所以
=9
a+
a
1
( )
2
所以
a +
a
1
=9
2
2
+
2
故
a
a
1
=7
2
+
2
因为
a+
a
1
=3
解:
知识巩固
(1)已知x=a+2b,y=a-2b,
(2)若(m+n)2=11,(m-n)2=7.求5mn的值
巩固练习1
求:x +xy+y
解:
∵ x=a+2b,y=a-2b
∴x+y=2a,xy=a -4b
∴x +xy+y =(x+y) -xy
=(2a) -(a -4b )
=3a +4b
解:
∵ (m+n)2=11,(m-n)2=7
∴ 4mn= (m+n)2-(m-n)2
=11-7
=4
∴mn=1
∴5mn=5
(3)已知a2-3a+1=0,求(1) (2)
(4)、已知 求x2-2x-3的值
解:
解:
∵a2-3a+1=0
∴ a2+1=3a
∴a+ = 3
∴ x2-2x-3
=2-3
= -1
已知:m2+n2+4m-6n+13=0,求mn的值。
巩固练习2
∵ m2+n2+4m-6n+13=0
∴ m2+4m+4+n2-6n+9=0
∴ (m+2)2+(n-3)2=0
∴ m=-2,n=3
∴mn=-6
解:
已知:x2+y2+6x-8y+25=0, 求x,y的值并化简求值
巩固练习2
∵ x2+y2+6x-8y+25=0
∴ x2+6x+9+y2-8y+16=0
∴ (x+3)2+(y-4)2=0
∴ x=-3,y=4
解:
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
巩固练习4
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1+x%)
a(1-x%)
a(1+x%) (1+x%)
= a(1+x%)2
a(1-x%) (1-x%)
= a(1-x%)2
甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%。
(1)5月份甲超市的销售额比乙超市多多少?
(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?
巩固练习5
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1+x%)
a(1+x%) (1+x%)
= a(1+x%)2
a(1-x%) (1-x%)
= a(1-x%)2
a(1-x%)
差额为:
a(1+x%)2-a(1-x%)2
=a(1+——+—— )
2x
100
10000
x2
= ——(万元)
25
ax
解:当a=150,x=2时,
—— = ———
25
ax
=12(万元)
25
150×2
要加油啊!
100
10000
-a(1 -——+—— )
2x
x2
(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?
第3课时 乘法公式综合练习
8.3 完全平方公式与平方差公式
沪科版数学七年级下
乘法公式
平方差公式
完全平方公式
(a+b)(a-b) =
a
2
b
2
-
(a+b)
2
=
a
2
b
2
2ab
+
+
二次三项型乘法公式
(x+a)(x+b)=
x +(a+b)x+ab
2
知识回顾
公式中的a、b即可以是数,也可以是含字母的代数式
比较平方差公式和完全平方公式:
(a-b)(a+b)= a2-b2
( a+ b)2=a2+2 a b+ b2
( a- b)2=a2-2 a b+ b2
公式 相乘多项式的特征 展开式项数
平方差公式 一项相同,另一项相反 2项
完全平方公式 两项都相同 3项
一、乘法公式基础练习
1、运用平方差公式进行计算:
(1)(-5x-3y)(-5x+3y)
解:
(1)(-5x-3y)(-5x+3y)
=(-5x) - (3y)
=25x -9y
解:
解:
应用平方差公式,结果是:
同号项 -异号项
(x-2y)( )
=
x
2
-4y
2
(1)
( )
-x
2
1
y
-
( )
=
x
2
+xy
+
4
1
y
2
(4)
x
-4y
(-x-2y)( )
=
2
2
(3)
( )
x
2
1
y
-
( )
=
x
2
-xy
+
4
1
y
2
(2)
x+2y
-x+2y
x-
2
1
y
-x-
2
1
y
2、运用平方差公式填空:
3、运用完全平方公式进行计算:
(2)原式=(5x+4) -(2x-3)
=25x +40x+16-(4x -12x+9)
=21x +52x+7
公式变形为
(首±尾)2=首2±2×首×尾+尾2
(1)(1-2x)(2x-1)
(3) (1-2x-3y)2
解:
解:
解:
(1)原式=-(2x-1)(2x-1)
=-(2x-1)
=-(4x -4x+1)
=-4x +4x-1
(3)原式=[(1-2x)-3y) ]2
=(1-2x) +2(1-2x)3y+(3y)
=1-4x+4x +6y-12xy+9y
(2)(-5x-4) -(2x-3)
4.下列各式是完全平方式的有( )
②
③ ④
A
①②③ B.②③④
C. ①②④ D.②④
D
1
+
-4
5、若|x+y-5|+(xy-6)2=0,则x2+y2的值为( )
A.13 B.26 C.28 D.37
A
例2.利用乘法公式简便计算:
103×97 (2)101 -99
(3)20222-2019×2025
解:
(1)原式=(100+3)×(100-3)=10000-9=9991
(2)原式=(100+1) -(100-1)
=10000+200+1-10000+200+1
=400
(3)原式=20222-(2022-3)×(2022+3)
= 20222- 20222+9
=9
=(10000-1)
=108-1=99999999
二、乘法公式提升 练习
(2)(-5x-4)(2x+3)(-5x+4)(2x-3)
(3)(-2x -5) -(-2x-5) (2x-5)
1、化简计算
解:
(2)原式=(-5x-4) (-5x+4)(2x+3)(2x-3)
=(25x -16)(4x -9)
=100x4-289x2+144
(3)原式=(4x4+20x+25)-[(-2x-5)(2x-5)]
= 4x4+20x+25-[2x -25]
=4x4+20x+25-(4x4-100x+625)
=120x-600
2、运用乘法公式计算
(1)、(a-2b+3)(a+2b-3)
(3)、( m 2n + 3 )2
(4)、 [(a+b)2+(a-b)2] (a2-b2)
(2)、 (3x2-4x+5)(3x2+4x-5)
=[a-(2b-3)][a+(2b-3)]
=a -2a(2b-3)+(2b-3)
= a -4ab+6a+4b -6b+9
(1)(a-2b+3)(a+2b-3)
解:
(2)、 (3x2-4x+5)(3x2+4x-5)
=[3x -(4x-5)][3x +(4x-5)]
=9x4-6x (4x-5)+(4x-5)
=9x4-24x3+30x +16x -40x+25
=9x4-24x3+46x -40x+25
(3)、( m 2n + 3 )2 =(m-2n) +6(m-2n)+9
=m -4mn+4n +6m-12n+9
(4)、 [(a+b)2+(a-b)2] (a2-b2)
=(2a +2b )] (a2-b2)
=2(a +b )(a2-b2)
=2(a4-b4)=2a4-2b4
(5)、 (x+2y+3z)2-(x-2y+3z)2
(5)、 (x+2y+3z)2-(x-2y+3z)2
=[ (x+3z)2+2×(x+3z)×2y+(2y) ]- [ (x+3z)2-2×(x+3z)×2y+(2y) ]
= 4×(x+3z)×2y
=8xy+24yz
三项组合为两项时,注意括进括号内的项尽量相同,后面化简方便计算
三、乘法公式拓展 练习
a
2
b
2
+
-
ab
+
=
(a+b)
2
(1)
a
2
b
2
+
-ab
+
=
(a-b)
2
(2)
2
(a+b)
-
(a-b)
2
=
(3)
2
(a+b)
+
(a-b)
2
=
(4)
a
2
b
2
+
=
(a+b)
2
+
(a-b)
2
+
=
(5)
3ab
(-ab)
4ab
2a
2
2b
2
+
(-2ab)
2ab
乘法公式变式
填空:
例 1 、已知a+b=5 ,ab= -2,
求(1) a2+b2 (2)a-b
a2+b2=(a+b)2-2ab
(a-b)2=(a+b)2-4ab
例题讲解
解:
(1) a2+b2=(a+b) -2ab
=5 -2×(-2)
=29
(2)∵(a-b) =(a+b)2-4ab
=5 -4×(-2)
=33
∴a-b=±
注意乘法公式变化规律
例2、 已知x+y=4,x2+y2=10,求xy和x-y的值.
解:由x+y=4,可得(x+y)2=16,
即 x2+2xy+y2=16.
∵ x2+y2=10,
∴ xy=3.
∵ (x-y)2=x2+y2-2xy=10-2×3=4,
∴ x-y=±2.
注意:由(x-y)2=4,求x-y,有两解,不能遗漏!
例3、如果a+的值
所以
=9
a+
a
1
( )
2
所以
a +
a
1
=9
2
2
+
2
故
a
a
1
=7
2
+
2
因为
a+
a
1
=3
解:
知识巩固
(1)已知x=a+2b,y=a-2b,
(2)若(m+n)2=11,(m-n)2=7.求5mn的值
巩固练习1
求:x +xy+y
解:
∵ x=a+2b,y=a-2b
∴x+y=2a,xy=a -4b
∴x +xy+y =(x+y) -xy
=(2a) -(a -4b )
=3a +4b
解:
∵ (m+n)2=11,(m-n)2=7
∴ 4mn= (m+n)2-(m-n)2
=11-7
=4
∴mn=1
∴5mn=5
(3)已知a2-3a+1=0,求(1) (2)
(4)、已知 求x2-2x-3的值
解:
解:
∵a2-3a+1=0
∴ a2+1=3a
∴a+ = 3
∴ x2-2x-3
=2-3
= -1
已知:m2+n2+4m-6n+13=0,求mn的值。
巩固练习2
∵ m2+n2+4m-6n+13=0
∴ m2+4m+4+n2-6n+9=0
∴ (m+2)2+(n-3)2=0
∴ m=-2,n=3
∴mn=-6
解:
已知:x2+y2+6x-8y+25=0, 求x,y的值并化简求值
巩固练习2
∵ x2+y2+6x-8y+25=0
∴ x2+6x+9+y2-8y+16=0
∴ (x+3)2+(y-4)2=0
∴ x=-3,y=4
解:
观察下列各组数,
请用字母表示它们的规律
……
n是正整数
巩固练习4
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1+x%)
a(1-x%)
a(1+x%) (1+x%)
= a(1+x%)2
a(1-x%) (1-x%)
= a(1-x%)2
甲、乙两家超市3月份的销售额均为a万元,在4月和5月这两个月中,甲超市的销售额平均每月增长x%,而乙超市的销售额平均每月减少x%。
(1)5月份甲超市的销售额比乙超市多多少?
(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?
巩固练习5
3月份
4月份
5月份
甲超市
销售额
乙超市
销售额
a
a
a(1+x%)
a(1+x%) (1+x%)
= a(1+x%)2
a(1-x%) (1-x%)
= a(1-x%)2
a(1-x%)
差额为:
a(1+x%)2-a(1-x%)2
=a(1+——+—— )
2x
100
10000
x2
= ——(万元)
25
ax
解:当a=150,x=2时,
—— = ———
25
ax
=12(万元)
25
150×2
要加油啊!
100
10000
-a(1 -——+—— )
2x
x2
(2)如果a=150,x=2,那么5月份甲超市的销售额
比乙超市多多少万元?
