北师大版七年级数学下册 三角形与重要的线(整理复习) 教案
文档属性
| 名称 | 北师大版七年级数学下册 三角形与重要的线(整理复习) 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 603.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-30 00:00:00 | ||
图片预览



文档简介
课题 三角形与重要的线(整理复习) 执教
学情分析 通过第四章《三角形》和第五章《生活中的轴对称》的学习,我发现学生对三角形的中线、高线、角平分线和垂直平分线的综合知识掌握的不好,有些学生甚至在概念上也发生混淆。所以我认为有必要把它们放在一起进行对比学习。
教学目标 知识技能 掌握三角形及中线、高线、角平分线和垂直平分线的定义、性质及角平分线和垂直平分线的尺规作图。
问题解决 通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,感受数学方法和数学模型思想的应用价值。
情感态度 通过小组交流,学生讲解,调动学生的学习积极性,激发学生的学习兴趣,树立科学的学习态度。
教学重点 梳理三角形及中线、高线、角平分线和垂直平分线的定义和性质。把知识点灵活应用到解典型例题中。
教学难点 在证明典型例题中总结出多个数学几何模型。
授课类型 新授课 课时 1课时
教学活动
教学步骤 师生活动 设计意图
课堂引入 师:进入期末复习阶段,有些同学对三角形中出现的各种线会有些模糊和混淆,那么我们这节课就来一起整理复习《三角形及重要的线》。
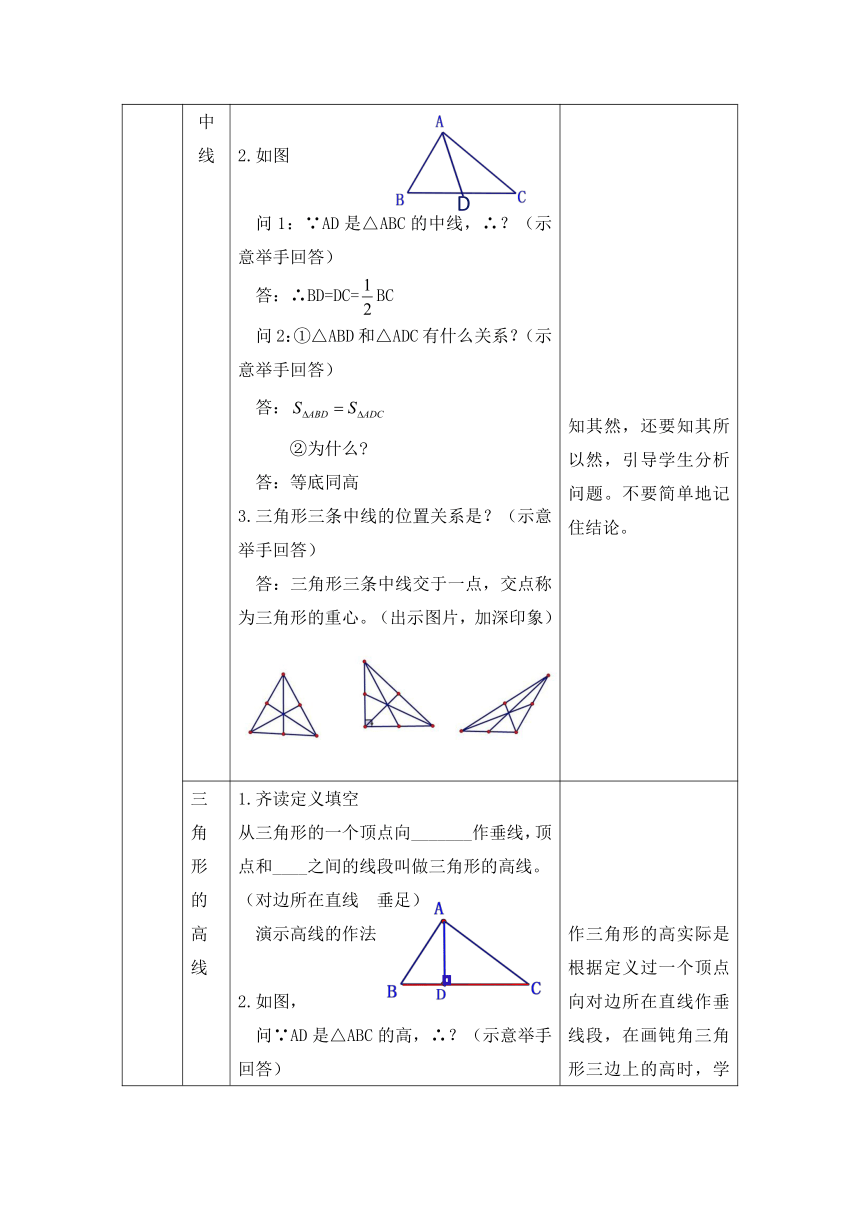
知识梳理 三角形的中线 齐读定义填空连接一个顶点与它_________的线段,叫作这个三角形的中线。(对边中点)如图问1:∵AD是△ABC的中线,∴?(示意举手回答) 答:∴BD=DC=BC 问2:①△ABD和△ADC有什么关系?(示意举手回答) 答: ②为什么 答:等底同高三角形三条中线的位置关系是?(示意举手回答) 答:三角形三条中线交于一点,交点称为三角形的重心。(出示图片,加深印象) 知其然,还要知其所以然,引导学生分析问题。不要简单地记住结论。
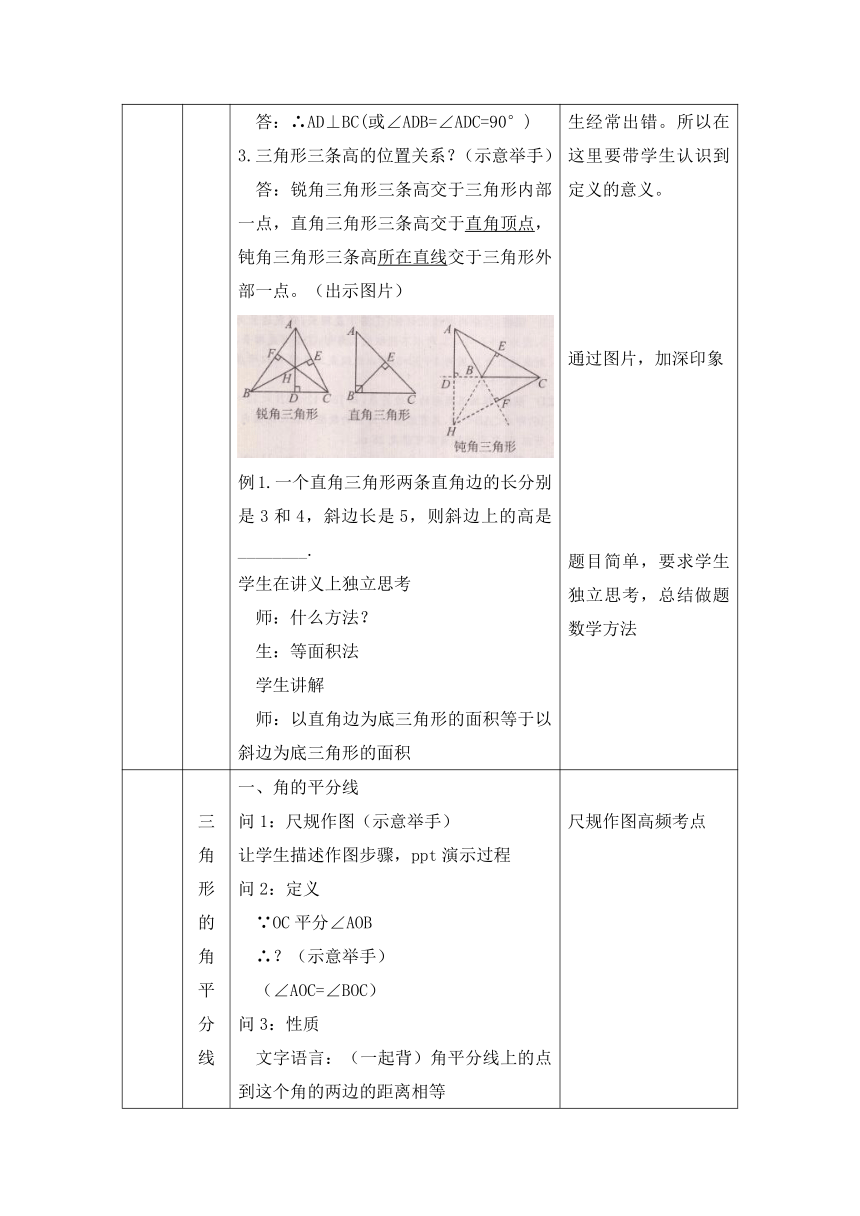
三角形的高线 齐读定义填空从三角形的一个顶点向_______作垂线,顶点和____之间的线段叫做三角形的高线。(对边所在直线 垂足)演示高线的作法如图,问∵AD是△ABC的高,∴?(示意举手回答) 答:∴AD⊥BC(或∠ADB=∠ADC=90°)三角形三条高的位置关系?(示意举手) 答:锐角三角形三条高交于三角形内部一点,直角三角形三条高交于直角顶点,钝角三角形三条高所在直线交于三角形外部一点。(出示图片)例1.一个直角三角形两条直角边的长分别是3和4,斜边长是5,则斜边上的高是________.学生在讲义上独立思考师:什么方法?生:等面积法学生讲解师:以直角边为底三角形的面积等于以斜边为底三角形的面积 作三角形的高实际是根据定义过一个顶点向对边所在直线作垂线段,在画钝角三角形三边上的高时,学生经常出错。所以在这里要带学生认识到定义的意义。通过图片,加深印象题目简单,要求学生独立思考,总结做题数学方法
三角形的角平分线 角的平分线问1:尺规作图(示意举手)让学生描述作图步骤,ppt演示过程问2:定义 ∵OC平分∠AOB ∴?(示意举手) (∠AOC=∠BOC)问3:性质 文字语言:(一起背)角平分线上的点到这个角的两边的距离相等 符号语言:(示意举手)∵OC平分∠AOB PE⊥OA,PF⊥OB ∴PE=PF三角形的角平分线齐读定义填空:在三角形中,一个内角的______与它的对边相交,这个角的顶点与_____之间的线段叫三角形的角平分线。师:角的平分线的定义和性质可以直接应用到三角形的角平分线中。例2.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=8,BD=5,则点D到AB的距离是多少?边读题边在图中标条件师:点D到AB的距离指的是什么?(示意举手)生:指点D到AB垂线段的长度师:这道题你会做吗?生:会师:我们一起来看这位同学的解题过程对不对?生:不对师:错哪儿了?生:没有说明垂直师:作辅助线的这句话可以修改为?生:过点D作DE⊥AB于点E还需要说明∠C=90°师:应用角平分线的性质一定记得一个平分,两个垂直问4:三角形三条角平分线的位置关系?(示意举手)生:三角形三条角平分线交于三角形内部一点。问5:以锐角三角形为例,从三角形三条角平分线的交点O向△ABC三边作垂线段OD、OE、OF,你有什么发现?(示意举手)生:OD=OE=OF师:谁能推理出来?(示意举手)生:∵BO平分∠ABC OD⊥OE,OE⊥AC∴OD=OE∵AO平分∠BAC OD⊥AB,OF⊥AC∴OD=OF∴OD=OE=OF填空:三角形三条角平分线的交点到三角形______的距离相等(三边)例3.如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO︰S△BCO︰S△CAO=________.独立思考,学生讲解 尺规作图高频考点带学生将数学几何定理与图形紧密结合在一起,发展几何逻辑语言。这道题属于基础题型同时是易错题型,学生都能做出结果,但经常在推理中少条件,通过投影学生的作业,让学生来批作业,从而加深对易错点的印象。学生对一些结论的记忆会随着时间淡忘,但基本的定理因为重复率较高,记得清楚,所以对于一些推论要让学生自己会推理。由刚刚的推论:三角形三条角平分线的交点到三角形三边的距离相等,立马应用到题中,学以致用。
线段垂直平分线 问1:尺规作图(示意举手)生边说作法边用ppt演示问2 :定义∵MN是AB的垂直平分线∴?(MN⊥AB,AO=BO)问3:性质文字语言:垂直平分线上的点到这条线段两个端点的距离相等符号语言:∵MN是AB的垂直平分线 ∴? (PA=PB)师:PA=PB,△PAB是等腰三角形,紧接着经常用到什么?生:∠A=∠B师:哪条性质?生:等腰三角形两底角相等。问4:三角形三边垂直平分线的位置关系?生:锐角三角形三边垂直平分线交于三角形内部一点,直角三角形三边垂直平分线交于斜边中点,钝角三角形三边垂直平分线交于三角形外部一点。(出示图片)问5:如图 ∵P是△ABC三边垂直平分线的交点(示意举手)∴?(示意举手)师:谁来推理?生:∵PD是AB的垂直平分线∴AP=BP∵PE是AC的垂直平分线∴AP=CP∴AP=BP=CP填空:三角形三边垂直平分线的交点到三角形______的距离相等(三个顶点)例4如图,在△ABC中,AB=AC,∠A=36°,DE垂直平分AB,△BEC的周长为20,BC=9.(1)求△ABC的周长(2)求∠EBC的度数独立思考,小组交流,让学生来当小老师讲题 题目出现MN是AB的垂直平分线,一般先反应性质:PA=PB,题目中如果关于角,那又可得出∠A=∠B。这是解题的规律。注重推论地推理,即使忘记,也可以根据基础定理去推导做垂直平分线时的必考题型,应用总结的知识点解题。小组互帮补助,学生当小老师,增加新鲜感,锻炼学生的分析解题思维
综合应用 典型题 5.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB. (2)AF=2CD.第(1)问分析:师:审题,要证△AEF≌△CEB,已经出现几个条件?生:两个。AB=AC,∠AEF=∠CEB=90°师:还差几个条件?生:1个师:找角还是找边?生:找角师:请同学们先思考,再小组交流,补全解题过程。证明:∵AD⊥BC,CE⊥AB ∴∠AEF=∠CEB=90° 在△AEF和△CEB中 AE=CE ∠AEF=∠CEB ∴△AEF≌△CEB.学生分析出三种不同的做法法1:法2:法3师生总结出三种几何模型第(2)问师引导生分析:要证AF=2CD,由第(1)问△AEF≌△CEB得AF=BC,则只需证BC=2CD,如何证?生:∵AB=AC,AD⊥BC ∴BC=2CD(等腰三角形三线合一) 这道题综合了三角形全等和等腰三角形三线合一知识。其中找相等的角是很典型的类型。可以分离出三种不同的模型。问先分析题目,找到这道题的难点,让学生去交流填空,把自己的方法和同学的交流,取长补短。问结合(1)问结论,分析出重点,应用等腰三角形三线合一(顶角的平分线、底边上的中线,底边上的高重合)
归纳与反思 知识归纳 通过学生自主填表,进一步建构知识结构 反思,更进一步地提升
总结反思
教学反思 1.授课流程反思复习旧知加深学生地印象,完善知识结构。在应用知识解决问题时,注重学生数学方法和数学模型的积累。讲授效果反思通过有限的4年教龄,我发现在教学中要重视复习课,学生的层次不一样,出现课后不复习,遗忘知识的现象,以至于考试中出现的基础题都不会做。复习课不是简单的知识重复,而是需要将知识整合,题型分类,让学生在题海中解放出来,培养学生分析、比较、归纳概括地思维能力。师生互动反思 教师用一个个问题引导学生将知识串起来,解决问题时,先带学生找出问题的关键点,在此基础上小组交流,这样讨论可以有针对性地进行,教师对学生的引导比较准确,比较好地体现了知识的生成过程。
D
D
E
F
∴∠1+∠B=90°
∠2+∠B=90°
∴∠1=∠2
∴∠1+∠3=90°
∠2+∠4=90°
∴∠3=∠4
∴∠1=∠2
∴∠1+∠3=90°
∵AD⊥BC
∴∠1+∠B=90°
∴∠3=∠B
学情分析 通过第四章《三角形》和第五章《生活中的轴对称》的学习,我发现学生对三角形的中线、高线、角平分线和垂直平分线的综合知识掌握的不好,有些学生甚至在概念上也发生混淆。所以我认为有必要把它们放在一起进行对比学习。
教学目标 知识技能 掌握三角形及中线、高线、角平分线和垂直平分线的定义、性质及角平分线和垂直平分线的尺规作图。
问题解决 通过对例题的分析,培养学生分析总结问题的习惯,提高学生综合运用知识解题的能力,感受数学方法和数学模型思想的应用价值。
情感态度 通过小组交流,学生讲解,调动学生的学习积极性,激发学生的学习兴趣,树立科学的学习态度。
教学重点 梳理三角形及中线、高线、角平分线和垂直平分线的定义和性质。把知识点灵活应用到解典型例题中。
教学难点 在证明典型例题中总结出多个数学几何模型。
授课类型 新授课 课时 1课时
教学活动
教学步骤 师生活动 设计意图
课堂引入 师:进入期末复习阶段,有些同学对三角形中出现的各种线会有些模糊和混淆,那么我们这节课就来一起整理复习《三角形及重要的线》。
知识梳理 三角形的中线 齐读定义填空连接一个顶点与它_________的线段,叫作这个三角形的中线。(对边中点)如图问1:∵AD是△ABC的中线,∴?(示意举手回答) 答:∴BD=DC=BC 问2:①△ABD和△ADC有什么关系?(示意举手回答) 答: ②为什么 答:等底同高三角形三条中线的位置关系是?(示意举手回答) 答:三角形三条中线交于一点,交点称为三角形的重心。(出示图片,加深印象) 知其然,还要知其所以然,引导学生分析问题。不要简单地记住结论。
三角形的高线 齐读定义填空从三角形的一个顶点向_______作垂线,顶点和____之间的线段叫做三角形的高线。(对边所在直线 垂足)演示高线的作法如图,问∵AD是△ABC的高,∴?(示意举手回答) 答:∴AD⊥BC(或∠ADB=∠ADC=90°)三角形三条高的位置关系?(示意举手) 答:锐角三角形三条高交于三角形内部一点,直角三角形三条高交于直角顶点,钝角三角形三条高所在直线交于三角形外部一点。(出示图片)例1.一个直角三角形两条直角边的长分别是3和4,斜边长是5,则斜边上的高是________.学生在讲义上独立思考师:什么方法?生:等面积法学生讲解师:以直角边为底三角形的面积等于以斜边为底三角形的面积 作三角形的高实际是根据定义过一个顶点向对边所在直线作垂线段,在画钝角三角形三边上的高时,学生经常出错。所以在这里要带学生认识到定义的意义。通过图片,加深印象题目简单,要求学生独立思考,总结做题数学方法
三角形的角平分线 角的平分线问1:尺规作图(示意举手)让学生描述作图步骤,ppt演示过程问2:定义 ∵OC平分∠AOB ∴?(示意举手) (∠AOC=∠BOC)问3:性质 文字语言:(一起背)角平分线上的点到这个角的两边的距离相等 符号语言:(示意举手)∵OC平分∠AOB PE⊥OA,PF⊥OB ∴PE=PF三角形的角平分线齐读定义填空:在三角形中,一个内角的______与它的对边相交,这个角的顶点与_____之间的线段叫三角形的角平分线。师:角的平分线的定义和性质可以直接应用到三角形的角平分线中。例2.如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D.若BC=8,BD=5,则点D到AB的距离是多少?边读题边在图中标条件师:点D到AB的距离指的是什么?(示意举手)生:指点D到AB垂线段的长度师:这道题你会做吗?生:会师:我们一起来看这位同学的解题过程对不对?生:不对师:错哪儿了?生:没有说明垂直师:作辅助线的这句话可以修改为?生:过点D作DE⊥AB于点E还需要说明∠C=90°师:应用角平分线的性质一定记得一个平分,两个垂直问4:三角形三条角平分线的位置关系?(示意举手)生:三角形三条角平分线交于三角形内部一点。问5:以锐角三角形为例,从三角形三条角平分线的交点O向△ABC三边作垂线段OD、OE、OF,你有什么发现?(示意举手)生:OD=OE=OF师:谁能推理出来?(示意举手)生:∵BO平分∠ABC OD⊥OE,OE⊥AC∴OD=OE∵AO平分∠BAC OD⊥AB,OF⊥AC∴OD=OF∴OD=OE=OF填空:三角形三条角平分线的交点到三角形______的距离相等(三边)例3.如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO︰S△BCO︰S△CAO=________.独立思考,学生讲解 尺规作图高频考点带学生将数学几何定理与图形紧密结合在一起,发展几何逻辑语言。这道题属于基础题型同时是易错题型,学生都能做出结果,但经常在推理中少条件,通过投影学生的作业,让学生来批作业,从而加深对易错点的印象。学生对一些结论的记忆会随着时间淡忘,但基本的定理因为重复率较高,记得清楚,所以对于一些推论要让学生自己会推理。由刚刚的推论:三角形三条角平分线的交点到三角形三边的距离相等,立马应用到题中,学以致用。
线段垂直平分线 问1:尺规作图(示意举手)生边说作法边用ppt演示问2 :定义∵MN是AB的垂直平分线∴?(MN⊥AB,AO=BO)问3:性质文字语言:垂直平分线上的点到这条线段两个端点的距离相等符号语言:∵MN是AB的垂直平分线 ∴? (PA=PB)师:PA=PB,△PAB是等腰三角形,紧接着经常用到什么?生:∠A=∠B师:哪条性质?生:等腰三角形两底角相等。问4:三角形三边垂直平分线的位置关系?生:锐角三角形三边垂直平分线交于三角形内部一点,直角三角形三边垂直平分线交于斜边中点,钝角三角形三边垂直平分线交于三角形外部一点。(出示图片)问5:如图 ∵P是△ABC三边垂直平分线的交点(示意举手)∴?(示意举手)师:谁来推理?生:∵PD是AB的垂直平分线∴AP=BP∵PE是AC的垂直平分线∴AP=CP∴AP=BP=CP填空:三角形三边垂直平分线的交点到三角形______的距离相等(三个顶点)例4如图,在△ABC中,AB=AC,∠A=36°,DE垂直平分AB,△BEC的周长为20,BC=9.(1)求△ABC的周长(2)求∠EBC的度数独立思考,小组交流,让学生来当小老师讲题 题目出现MN是AB的垂直平分线,一般先反应性质:PA=PB,题目中如果关于角,那又可得出∠A=∠B。这是解题的规律。注重推论地推理,即使忘记,也可以根据基础定理去推导做垂直平分线时的必考题型,应用总结的知识点解题。小组互帮补助,学生当小老师,增加新鲜感,锻炼学生的分析解题思维
综合应用 典型题 5.如图,△ABC中,AB=AC,AD⊥BC,CE⊥AB,AE=CE.求证:(1)△AEF≌△CEB. (2)AF=2CD.第(1)问分析:师:审题,要证△AEF≌△CEB,已经出现几个条件?生:两个。AB=AC,∠AEF=∠CEB=90°师:还差几个条件?生:1个师:找角还是找边?生:找角师:请同学们先思考,再小组交流,补全解题过程。证明:∵AD⊥BC,CE⊥AB ∴∠AEF=∠CEB=90° 在△AEF和△CEB中 AE=CE ∠AEF=∠CEB ∴△AEF≌△CEB.学生分析出三种不同的做法法1:法2:法3师生总结出三种几何模型第(2)问师引导生分析:要证AF=2CD,由第(1)问△AEF≌△CEB得AF=BC,则只需证BC=2CD,如何证?生:∵AB=AC,AD⊥BC ∴BC=2CD(等腰三角形三线合一) 这道题综合了三角形全等和等腰三角形三线合一知识。其中找相等的角是很典型的类型。可以分离出三种不同的模型。问先分析题目,找到这道题的难点,让学生去交流填空,把自己的方法和同学的交流,取长补短。问结合(1)问结论,分析出重点,应用等腰三角形三线合一(顶角的平分线、底边上的中线,底边上的高重合)
归纳与反思 知识归纳 通过学生自主填表,进一步建构知识结构 反思,更进一步地提升
总结反思
教学反思 1.授课流程反思复习旧知加深学生地印象,完善知识结构。在应用知识解决问题时,注重学生数学方法和数学模型的积累。讲授效果反思通过有限的4年教龄,我发现在教学中要重视复习课,学生的层次不一样,出现课后不复习,遗忘知识的现象,以至于考试中出现的基础题都不会做。复习课不是简单的知识重复,而是需要将知识整合,题型分类,让学生在题海中解放出来,培养学生分析、比较、归纳概括地思维能力。师生互动反思 教师用一个个问题引导学生将知识串起来,解决问题时,先带学生找出问题的关键点,在此基础上小组交流,这样讨论可以有针对性地进行,教师对学生的引导比较准确,比较好地体现了知识的生成过程。
D
D
E
F
∴∠1+∠B=90°
∠2+∠B=90°
∴∠1=∠2
∴∠1+∠3=90°
∠2+∠4=90°
∴∠3=∠4
∴∠1=∠2
∴∠1+∠3=90°
∵AD⊥BC
∴∠1+∠B=90°
∴∠3=∠B
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
